Evaluation Model of Rural Drinking Water Project Based on Entropy Weight and Fuzzy Comprehensive Evaluation Method

Zhijun SU1*, Guanghua WANG1, Jiahao YAN1, Chaoju DONG

1. School of Economics and Information, Zhejiang Tongji Vocational College of Science and Technology, Hangzhou 311231, China; 2. Water Resources Bureau of Pujiang County, Jinhua 322200, China

Abstract Based on Measures for Assessment of Rural Drinking Water Standard Raising Action in Zhejiang Province, this study established an evaluation system for rural drinking water project in Zhejiang Province, covering three primary indicators of project construction, project management and project performance, and 18 secondary indicators. It proposed an evaluation model based on entropy weight and fuzzy evaluation method. It solved the problems of the objectivity of the indicator weight and the quantification of the indicators, and can well achieve the coordination and unity of fuzziness and accuracy. Using this model, it evaluated a rural drinking water project in a county and concluded that both accuracy and feasibility of the model are high.

Key words Entropy weight method, Fuzzy comprehensive evaluation method, Rural drinking water

1 Introduction

In recent years, Zhejiang Province has vigorously promoted the improvement of rural drinking water standards, and counties and cities in the province also have gradually established agricultural drinking water systems with large-scale development, standardized construction, market-oriented operation, and professional management. Due to the geographical characteristics of Zhejiang Province, the drinking water projects generally have problems such as small scale, scattered distribution, imperfect facilities, and non-standard management. These bring a certain difficulty to objectively evaluate the agricultural drinking water work in various areas. The existing evaluation system is not very objective in determining the weight of each evaluation indicator, which prejudices the credibility of the results. In addition, because the evaluation of rural drinking water is a non-linear process with unclear goals, it presents certain fuzzy characteristics in terms of indicator content, expression form and evaluation results. Therefore, it is urgently necessary to establish a scientific and practical evaluation system[1]. Combining the entropy weight method and the fuzzy comprehensive evaluation method not only solves the objectivity problem of the indicator weight, but also solves the fuzziness problem of the indicators. It can make the evaluation work professional, scientific and standardized, bring the incentive effect of the assessment, and provide decision-making basis and reference for the follow-up project construction.

2 Establishment of the evaluation indicator system

Rural drinking water project involve many factors. Apart from the project construction situation, it is also necessary to consider the daily management and operation work and overall benefit. Taking a county in Zhejiang Province as the research object, based onMeasuresforAssessmentofRuralDrinkingWaterStandardRaisingActioninZhejiangProvince, with the reference to the existing research results, following the principles of science, application and operability[2], we divided the rural drinking water project into three primary indicators, namely construction management, operation management and performance management, and then subdivided into 18 secondary indicators. Because the provincial standard of Zhejiang Province is higher than the national standard, we complied with the following principle when formulating the scoring standard: Those that meeting the national standards were rated as Level I (90 points), and those not meeting the national standards were rated and scored by scoring experts according to the actual situation. The evaluation system and criteria are shown in Table 1.

3 Construction of evaluation model based on entropy weight-fuzzy comprehensive evaluation method

The entropy weight method is an objective weighting method and it only depends on the discreteness of the data itself. Compared with the subjective weighting method, the entropy weighting method is more objective and has higher precision. Fuzzy comprehensive evaluation method is a comprehensive evaluation method based on fuzzy mathematics. It transforms qualitative evaluation into quantitative evaluation according to the membership degree theory of fuzzy mathematics, that is, to use fuzzy mathematics to make a general evaluation of things or objects restricted by many factors. It is characterized by clear results and strong systematicness. It can better solve fuzzy problems that are difficult to quantify, and is suitable for solving various non-deterministic problems.

In the evaluation of agricultural drinking water projects, there are many indicators that are difficult to quantify, such as social benefits,etc.It is difficult to make quantitative analysis, but have to make qualitative analysis, and it is necessary to avoid relying too much on the subjectivity of experts in determining the weight of indicators. In this study, through combining the characteristics of the entropy weight method and the fuzzy comprehensive evaluation method, we not only identified the differences between the evaluation results under equal weight and unequal weight[3], but also solved the evaluation factors that are fuzzy and difficult to quantify. We transformed qualitative evaluation into quantitative evaluation to achieve the unity of fuzziness and precision[4].

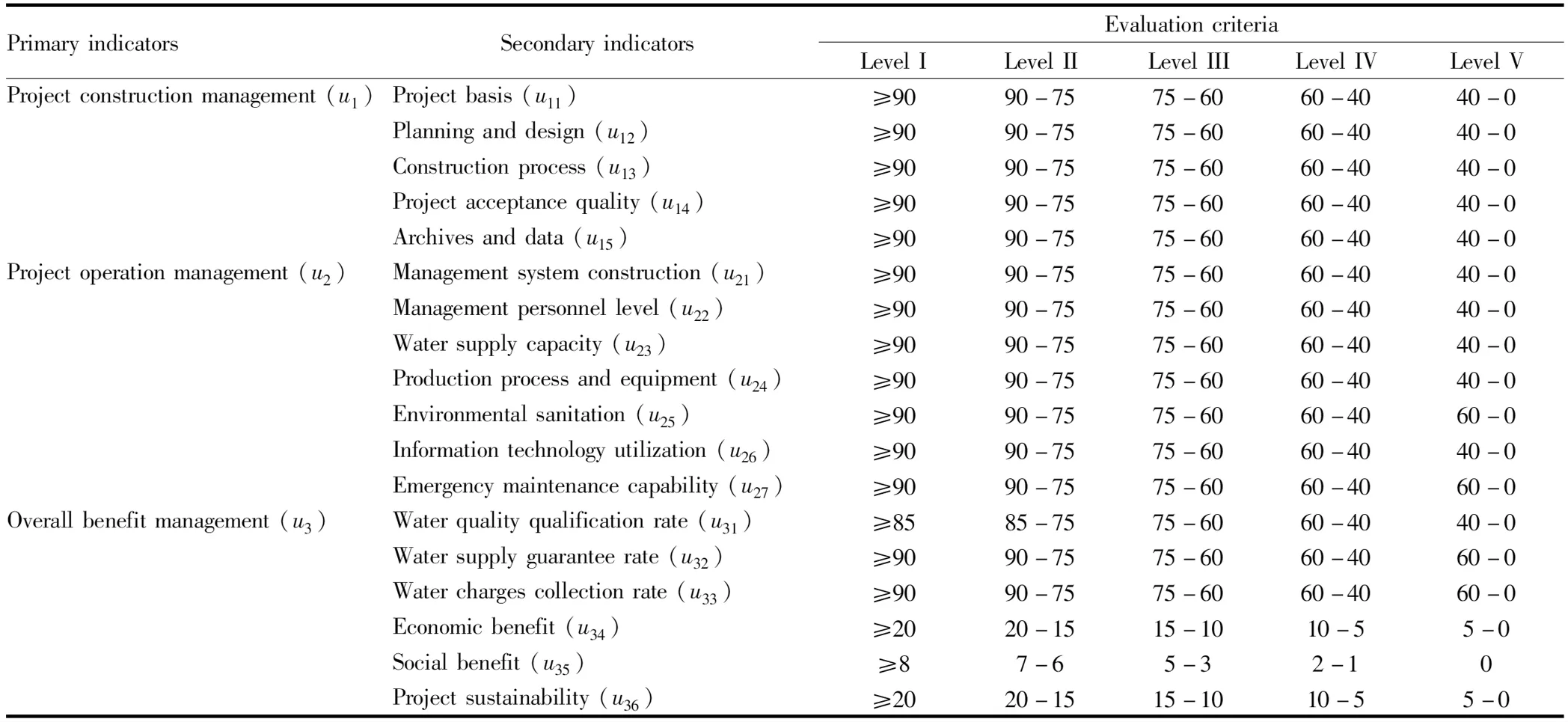
Table 1 Evaluation indicator system and criteria of rural drinking water project in Zhejiang Province

3.1 Determination of the weight of evaluation indicators using entropy weight method[5-6]

3.1.1Establishment of the original data evaluation matrixK.

wherekijdenotes the final evaluation score of thejthevaluation indicator of theithsample. According to Table 1, there are 18 evaluation indicators, som=18.

3.1.2Normalization processing. Normalization is to convert the absolute value of the initial evaluation matrix of indicators into relative values, so as to solve the homogeneity problem of various indicators of heterogeneous indicators. Using the formula (1), we processed theKmatrix and obtained the normalized standard matrix. The calculation formula is as follows:

(1)

3.1.3Calculation of the evaluation criteria matrixP. This is to calculate the proportion of theithsample value under thejthindicator to the indicator, and the evaluation standard matrixPis:

(2)

3.1.4Calculation of the information entropy of each indicator. The information entropy of thejthindicator is calculated by the formula (3):

(3)

3.1.5Calculation of the weight of each indicator. The weight of thejthindicator is calculated by the formula (4):

(4)

3.2 Determination of the evaluation score using the fuzzy comprehensive evaluation method[6-7]

3.2.1Determination of the evaluation indicator set. We determined the evaluation indicator setUaccording to the evaluation factors of the evaluation indicator system.U={u1,u2,u3, …,um}.

3.2.2Determination of the finite setVof evaluation levels. According to actual needs, we divided the evaluation intonlevels.V={v1,v2,v3, …,vn}. According to the actual situation such as the operability of the evaluation of rural drinking water projects, we divided the evaluation into 5 levels, namely very goodv1, goodv2, generalv3, poorv4and very poorv5. The score ranges are: [90, 100], [80,90), [70,80), [60,70), [0,60). Then, we assigned the scores from high to low,V={v1,v2,v3,v4,v5}, if the score is 90-100, it means that the evaluation is very good, and other score levels can be obtained in the same way.

3.2.3Determination of the membership degree evaluation indicator. We made a statistic of the number of experts whose indicator factors belong to five levels: very good, good, general, poor and very poor. Then, we divided the number of experts at each evaluation level by the total number of experts as the membership degree valuermuiof the evaluation factoruito the evaluation levelvn(n=1, 2, 3, 4, 5). The membership degree matrixRof each factor is expressed as:

3.2.4Evaluation of fuzzy relation synthesis. Using the entropy weight method, we obtained the weight setWof 18 indicator factors.W={w1,w2, …,wm} Then, by correlating the weight index set with the index fuzzy matrix, we comprehensively evaluated the evaluation indicator, and the evaluation vectorBis calculated by the formula (5):

B=W·R

(5)

3.2.5Determination of the evaluation score. In order to avoid the problem that the membership degree value is similar in the principle of maximum membership degree and it is difficult to accurately judge the evaluation level, we adopted the weighted average judgment model, took the median of {v1,v2,v3,v4,v5} and assigned scores from high to low.V={95, 85, 75, 65, 30} The evaluation scoreDof rural drinking water operation and management can be calculated by the formula (6):

D=V·B-1

(6)

4 Case application

4.1 Overview of the caseThe case county is located in the hilly area in the central part of Zhejiang Province. In the county, there are abundant water resources. Rural drinking water projects have problems of small scale, scattered distribution, lack of construction funds and maintenance funds, poor management after construction. From 2017, the county actively carried out the assessment of rural drinking water qualification, promoting construction and reform through evaluation. After years of development, the situation has been greatly improved. The case took a rural drinking water project as the research object. The project belonged to a township water plant, had a daily water supply of 5 000 t, benefited 19 165 people, had 10 water plant managers, 8 with training certificates, 3 with vocational qualification certificates, and the plant had obtained the license for drawing water and hygiene license.

4.2 Determination of indicator weightsWhen determining the weight by the entropy weight method, we selected the scoring data of 10 representative projects in the county in 2020 as samples. The scoring data adopted the method of subjectively determining the weight and taking the mean of expert scores as the final score. The results are indicated in Table 2.

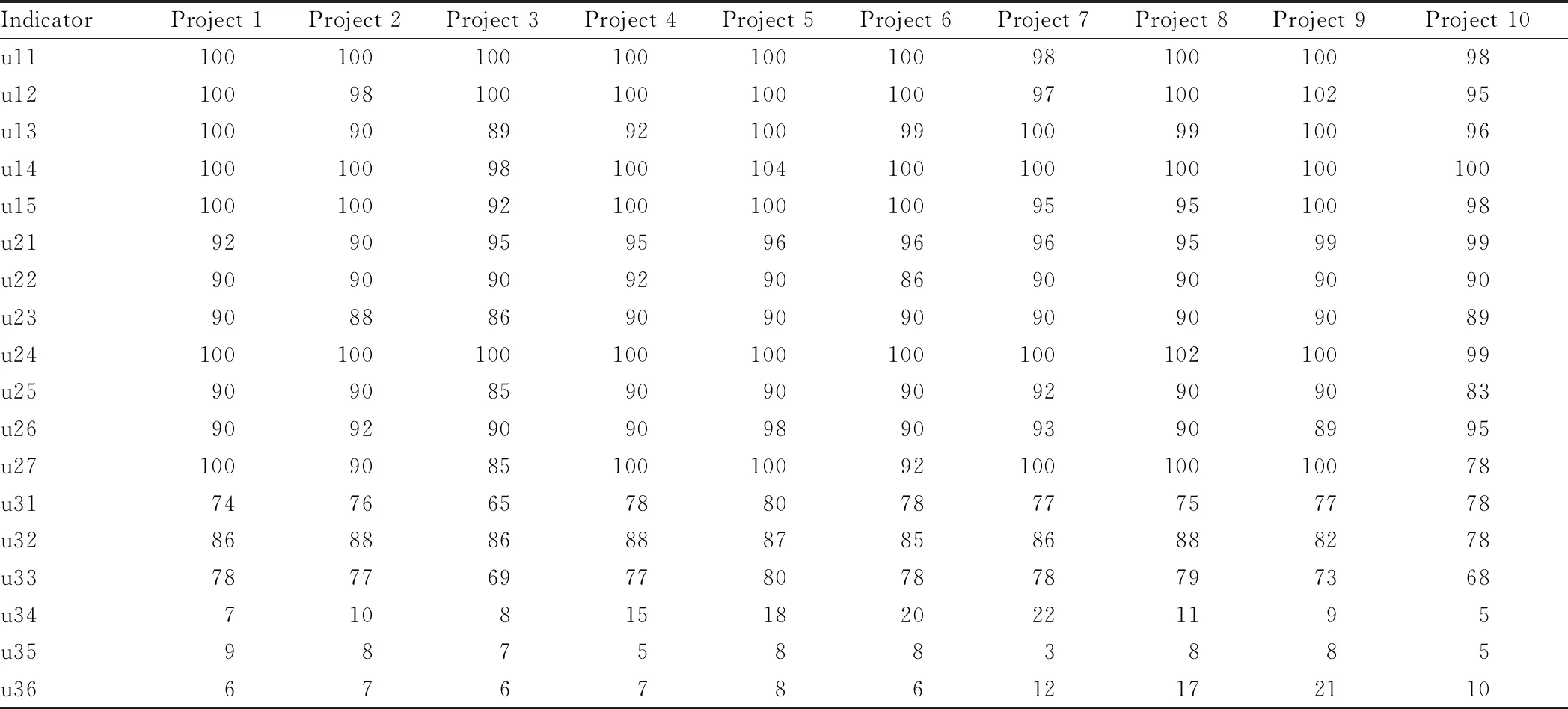
Table 2 Indicator scores of 10 representative projects in a county of Zhejiang Province in 2020

According to the scoring results, we finally obtained the weight vector of 18 indicators using the entropy weight method. The result is as follows:W=(0.056, 0.038, 0.058, 0.051, 0.04, 0.042, 0.029, 0.031, 0.051, 0.037, 0.116, 0.039, 0.029, 0.033, 0.051, 0.077, 0.04, 0.182).

4.3 Calculation of evaluation scoresWe invited 10 experts and technicians to score, including 2 water conservancy experts, 2 engineering project managers, 3 engineering management personnel, and 3 experts engaged in rural drinking water evaluation. Then, we evaluated each individual indicator of the indicator set against the evaluation scoring standard. According to the membership degree calculation formula, we obtained the evaluation membership degreeRof each indicator. From the formula (5), we obtained the matrixB. From the formula (6), we obtained the final scoreDof this project, the result is:

5 Conclusions

In view of the problems of the current rural drinking water project evaluation system, we put forward the actual evaluation indicators for Zhejiang Province. Using the entropy weight method, we assigned the indicator weight, which overcomes the subjectivity of the indicator weight assignment and improves the accuracy. Besides, we introduced fuzzy comprehensive evaluation method and followed the principle of fuzzy relation synthesis to make fuzzy comprehensive evaluation, so as to make the evaluation more objective. Using this evaluation model, we evaluated a township water plant in a county in Zhejiang Province, the final score was 87.5, which is good and above, and is close to the evaluation score of the project in 2020. This verified the accuracy and feasibility of the model, and is expected to provide a certain reference for the evaluation of rural drinking water projects in Zhejiang Province.