2021 年高考“古典概型与几何概型”问题聚焦

■何 炜 刘大鸣(特级教师)

古典概型与几何概型是高中数学的重要内容之一,也是新高考的必考内容。古典概型的基本事件都是有限的,其概率等于事件所包含的基本事件个数除以总的基本事件个数。几何概型的基本事件通常不可计数,只能通过一定的测度,如长度,面积,体积的比值来表示。下面聚焦2021年高考“古典概型与几何概型”问题,希望对同学们的学习有所帮助。

一、利用枚举法计数,构建古典概型求概率

例1 (2021年高考全国卷) 将3个1和2个0随机排成一行,则2个0不相邻的概率为( )。

A.0.3 B.0.5 C.0.6 D.0.8

解:用枚举法排列计数,用古典概型公式计算概率。

素养:求古典概型概率的关键是求试验的基本事件的总数和事件A包含的基本事件的个数,这就需要正确列出基本事件,基本事件的主要表示方法有列举法、列表法和树状图法。解答本题的关键是正确计数,注意3个1和2个0分别为相同元素,不要误用排列计数。

二、复杂事件的概率借助“互斥事件合理分类,相互独立事件分步”求解

例2 (2021年新高考全国卷)有6个相同的球,分别标有数字1,2,3,4,5,6,从中有放回地随机取两次,每次取1个球,甲表示事件“第一次取出的球的数字是1”,乙表示事件“第二次取出的球的数字是2”,丙表示事件“两次取出的球的数字之和是8”,丁表示事件“两次取出的球的数字之和是7”,则( )。

A.甲与丙相互独立

B.甲与丁相互独立

C.乙与丙相互独立

D.丙与丁相互独立

解:弄清甲、乙、丙、丁事件的意义,再分别计算概率进行判断。

素养:本题涉及相互独立事件的判断。“独立”与“互斥”的区别:两事件互斥是指两个事件不可能同时发生,两事件相互独立是指一个事件发生与否对另一事件发生的概率没有影响(如有放回抽取模型)。两事件相互独立通常不互斥,两事件互斥通常不独立。若事件A,B互斥,则P(A+B)=P(A)+P(B),若事件A,B不互斥,则P(A+B)=P(A)+P(B)-P(AB),若事件A,B相互独立,则P(AB)=P(A)P(B)。对于复杂概率的计算:一般要先设出事件,准确地确定事件的性质,把问题化归为古典概型、互斥事件、独立事件、独立重复试验四类事件中的某一种;然后判断事件是A+B还是AB事件,确定事件至少有一个发生,还是同时发生,分别运用相加或相乘事件公式;最后选用相应的求古典概型、互斥事件、条件概率、独立事件、n次独立重复试验的概率公式求解。

三、一元变量的几何概型构建长度或角度比求解

素养:几何概型的特点是无限性和等可能性。基本事件可以抽象为点,尽管这些点是无限的,但它们所占据的区域都是有限的,因此可用“比例解法”求解几何概型的概率。当试验的结果等可能且构成的区域为长度或面积或体积时,考虑使用几何概型求解。

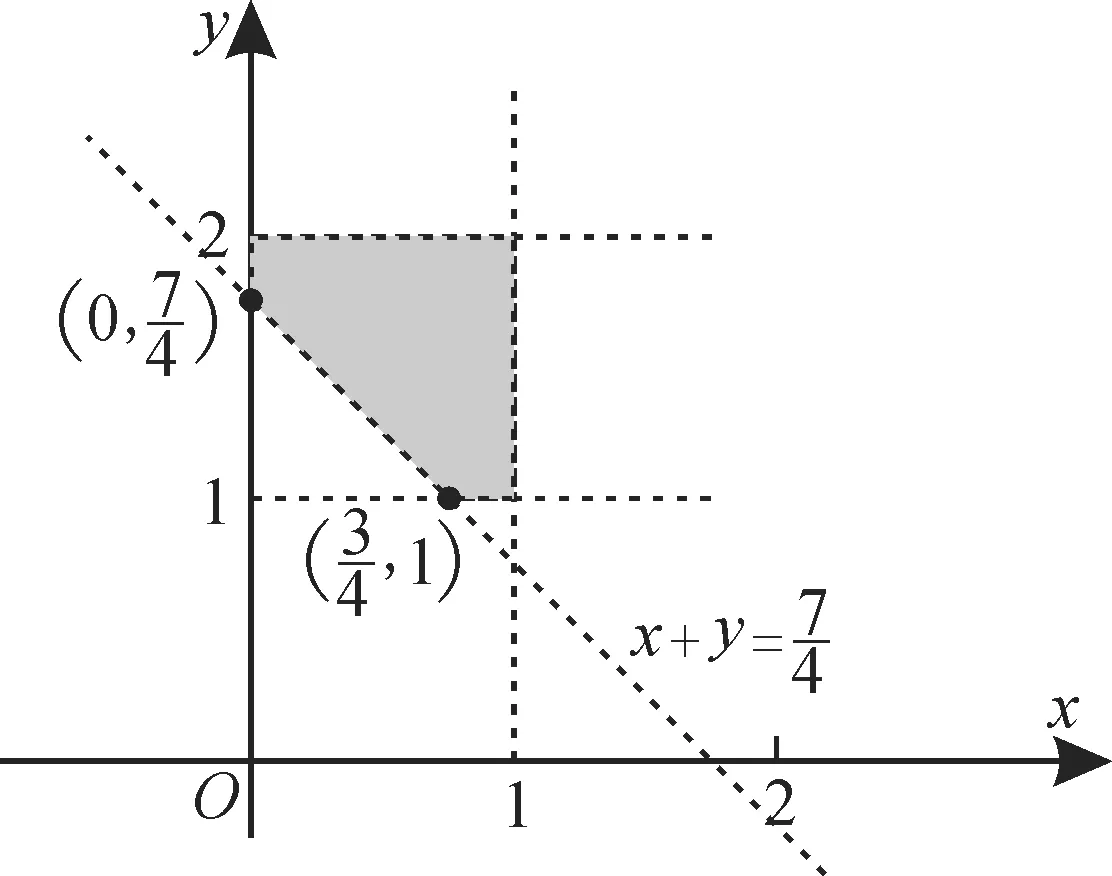
四、二元变量的几何概型构建面积比求解

解:二元变量的几何概型构建面积比,根据几何概型的概率公式求解。

设在区间(0,1)与(1,2)上随机取出的数分别为x,y,则试验的所有结果构成的区域Ω={(x,y)|0

图1

素养:求解二元变量几何概型的关键是把所取的两个数视作x,y,然后把点(x,y)看作点集区域,再利用面积测度求概率。解题时,弄清某事件对应的面积与全部试验结果构成的平面图形,以便求解。