基于高斯滤波的矿井RSSI定位算法研究

乔 欣 申海洋 况开通 李万豪 茆志魁

(巢湖学院 电子工程学院，安徽 巢湖 238000)

0 前 言

安全问题一直是全社会关注的热点问题。在煤矿安全生产管理中，要实时掌握井下人员数量、活动轨迹、精确位置、灾害位置等信息[1]。在发生事故时，及时准确的施救依赖于高精度的定位系统[2]。因此，研究井下定位算法非常重要[3]。

煤矿井下工人及机车的活动区域主要包括工作面、巷道等，与地面上的无线射频信号传输相比，煤矿井下的无线传输环境更复杂[4]。目前的定位技术主要包括蓝牙、RFID(Radio Frequency Identification)、WiFi、ZigBee、UWB(Ultra Wide Band)、超声波等[5]，而定位算法主要基于测距算法和非测距算法[6]。煤矿井下定位不同于地面定位，GPS无法发挥作用，且井下环境复杂多变，井上定位算法在井下应用的难度较大[7]。

针对矿井定位精度不高等问题，国内外学者提出了各种定位算法。王冬冬通过研究煤矿巷道的电磁波传播损耗规律，提出一种适合井下定位的AP规划方法，以满足数字矿山WLAN通信系统下移动终端的覆盖[8]。杨成等人通过研究巷道的长带状特征，提出一种基于WLAN区域划分的神经网络插值算法和基于信号强度权重指数的定位算法，与传统算法相比，该算法在计算复杂度及精度等方面有所提高[9]。韩东升等人通过分析巷道传输损耗模型，采用动态获取路径衰落指数的方法，提出一种基于接收信号强度(RSSI)的加权质心定位算法[10]。崔丽珍等人采用核函数法与粒子滤波算法对井下目标定位，实现了静态目标与动态目标的跟踪定位[11]。孙继平等人通过建立双路WiFi信道和信号收发计时方式，提出基于计时误差抑制的TOA煤矿井下目标定位方法[12]。吴静然等人提出一种改进的指纹定位算法，并将其与行人航迹推算(PDR)算法结合，以实现井下人员定位[13]。

针对井下定位算法的定位精度不高、计算开销过大等问题，在不增加节点硬件的前提下，提出一种基于高斯滤波的矿井RSSI定位算法(G-K-RSSI)。在定位的各个阶段，采用不同方案减小误差。测距阶段，对未知节点的RSSI进行高斯滤波处理，并取其平均值作为测量值。通过周期性动态测量待定位节点附近的锚节点之间的RSSI，计算并实时获取锚节点所在区域的无线传输功率衰落因数，结合无线信号传输模型，计算未知节点到锚节点之间的距离。定位阶段，充分利用未知节点与锚节点之间的误差，引入距离测量误差修正系数，采用最小二乘法求出未知节点的坐标。

1 基于RSSI矿井无线定位的问题分析

无线传感器网络中常用的信号传播模型为对数-常态分布模型[6]，如式(1)所示：

(1)

式中：P(d)——电磁波信号经过距离d后的信号强度；

P(d0)——电磁波信号经过距离d0后的信号强度，令d0=1 m；

k——路径损耗因子，反映周围环境对测距的影响程度，k通常为1～5；

ξn——均值为零、方差为σ的高斯随机变量，其标准差一般为2～10。

由式(1)可得出两节点之间的距离d：

(2)

当未知节点接收到3个或3个以上锚节点信息时，便可利用三边定位法或最小二乘法求解位置坐标[14]。

当k的取值不同时，RSSI与d之间的关系如图1所示。在理论与实际情况下，RSSI与d之间的关系如图2所示。

图1 k取值不同时RSSI与d的关系

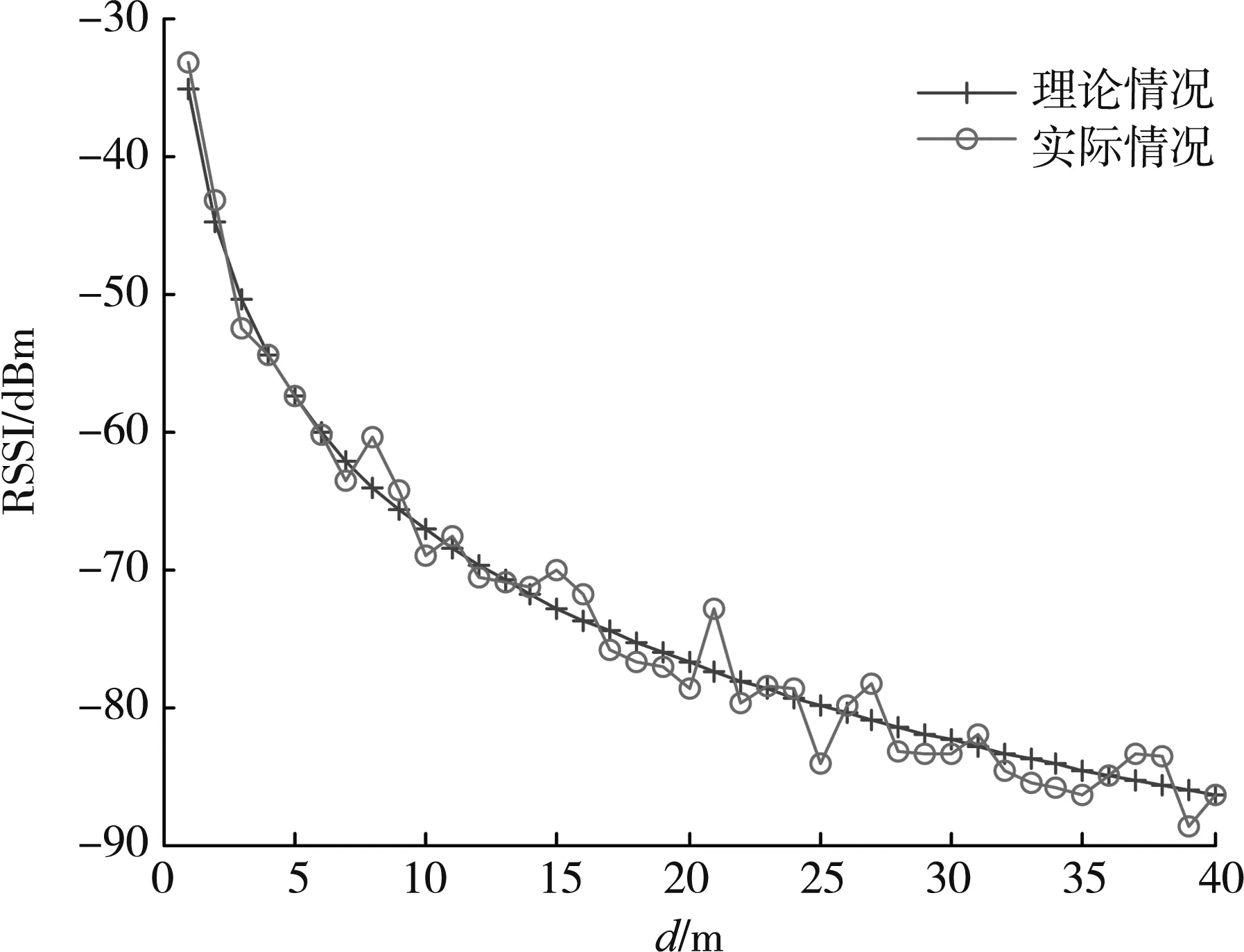
图2 理论与实际情况下RSSI与d的关系

从对数-常态分布模型来看，RSSI不仅与d有关，还与k有关。由于k是一个动态变化的参数，因此传统RSSI定位算法采用固定的k计算d，容易产生较大的测量误差。

2 基于G-K-RSSI的煤矿井下精确定位算法

2.1 RSSI高斯滤波预处理

在目标物体定位过程中，首先通过高斯滤波对未知节点接收到的RSSI进行滤波处理，然后求其有效值的算术平均，最后利用处理后的RSSI进行定位[15]。

设未知节点接收到n个RSSI采样值{x1,x2,x3，…，xn}，服从正态分布，且RSSI近似服从(μ,σ2)高斯分布，其概率密度函数如式(3)所示：

(3)

其中：

(4)

(5)

式中：μ——RSSI的均值，dBm；

σ——RSSI的标准差，dBm。

则F(x)的区间概率为：

P(|xi-μ|<σ)=2Φ(1)-1=0.683

Φ(x)为标准正态分布函数。选择高概率发生区的RSSI作为有效值，求其算术平均值：

(6)

对原始采样得到的RSSI与高斯滤波模型处理后的RSSI进行对比(见图3)可知，通过高斯滤波优化处理后的RSSI更平滑，去掉了测量突变数据和噪声波动。

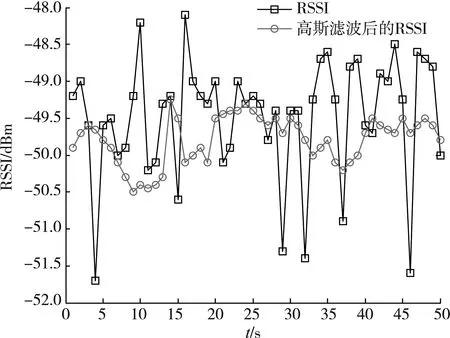
图3 高斯滤波修正前后对比

2.2 动态获取路径损耗因子

假设有N1、N2、N3等3个节点，未知节点N3接收到邻居节点N1、N2的RSSI，由式(1)可得：

(7)

(8)

两式相减可得：

(9)

式中：d1、d2分别为N3到N1、N2之间的实际距离；P(d1)、P(d2)分别为N3与N1、N2之间的RSSI。

由式(9)可知，k与P(d0)无关。利用未知节点到附近锚节点的实际距离，结合无线信号传输模型，计算并实时获取锚节点所在区域的k。在进行RSSI测距时使用实时动态损耗因子，可以有效地消除环境因素对测距精度的影响，进而获得准确的距离信息。

2.3 距离测量误差修正系数

建立符合矿井特殊环境的信号传输模型后，为了进一步提高定位精度，在计算未知节点到锚节点的距离di基础上，引入距离测量误差修正系数。

设未知节点坐标为(x,y)，锚节点的坐标为(xi,yi)，则未知节点到锚节点的距离di为：

(10)

整理可得：

AX+μ′=B

式中：μ′——(n-1)维随机误差向量。

由矩阵方程可得μ′=B-AX，μ′越小，定位越准确。采用最小二乘法求未知节点坐标的估计式为：

(11)

式中：Azheng——矩阵A与误差向量μ′之和。

2.4 算法实现

本次研究在RSSI定位算法的基础上，从测距精度、无线电传输模型、定位估计等方面进行了改进，改进算法流程如图4所示。

图4 改进算法流程图

3 实验结果分析

本次研究使用德州仪器公司生产的CC2530芯片[16]。CC2530芯片拥有无线信号的RSSI集成，数据通过网关汇聚采集后传输到上位机，利用Matlab完成编程。在实验室走廊5 m×50 m区域内布设定位基站，包括1个网关、4个参考节点、1个未知节点(见图5)，将实验室场景设置为狭长型，以模拟井下巷道环境。

图5 CC2530节点布设

节点i的定位误差Δdi为：

(12)

式中：xi、yi——锚节点坐标；

若节点个数为N，则平均定位误差E为：

(13)

在实验室走廊使用CC2530节点作为定位基站和未知节点，采集任意两点之间的RSSI。分别将锚节点分布在10种不同方案下进行多次测试，验证G-K-RSSI算法的有效性。传统RSSI算法的k=2，多次测量高斯滤波后的算术平均值，P(d0)=-36 dBm。两种算法的定位误差比较如图6所示，锚节点个数与平均定位误差的关系如图7所示。由图6可知，G-K-RSSI算法的平均定位误差为2.1 m，相较于传统RSSI算法，其定位精度和稳定性得到了明显提高。由图7可知，虽然两种定位算法的平均定位误差都随着锚节点个数的增加而减少，但G-K-RSSI算法的定位误差减少得更明显，定位精度更高。

图6 两种算法的定位误差比较

图7 锚节点个数与平均定位误差的关系

4 结 语

在不增加节点硬件开销的前提下，提出一种高斯滤波周期性动态测量路径损耗因子的接收信号强度煤矿井下定位算法。采用高斯滤波法对RSSI进行预处理，通过实时计算动态路径损耗因子来构建符合煤矿巷道环境的信号传输模型，以提高测距精度。充分利用未知节点与锚节点之间的误差，引入距离测量误差修正系数，采用最小二乘法求得未知节点坐标。实验结果表明，相同条件下G-K-RSSI算法的定位精度远高于传统RSSI算法。G-K-RSSI算法可以准确实现井下巷道定位，对于井下人员的安全调度、高效生产具有重要的指导意义。