热力站日供热量影响因素筛选与神经网络预测
2022-05-18王嘉明
1 概述
按需供热对降低热力站的能耗具有现实意义,也是提升供热效率的关键所在
。热负荷受气象参数、用户习惯、建筑保温性能等因素影响,因此热负荷预测是一项非常具有挑战性的任务
。热负荷影响因素的筛选和合理的预测方法是获得准确预测值的关键
。
付波
根据所研究热力站的区域特点和负荷特征,分析出热负荷的显著影响因素有室外温度、风速等,并作为输入元素引入用遗传算法优化的BP神经网络预测模型。Geysen等人
结合瑞典罗特内的10座住宅建筑特征以及天气预报服务提供的室外温度进行热负荷预测和验证。朱冬雪等人
根据热力站特征分析出室外空气相对湿度、风速、太阳辐射、室外平均温度是主要影响因素,通过建立热负荷BP神经网络预测模型使供热系统改造后总能耗降低9.5%。刘也
经过影响因素的筛选及相关性分析,将室外温度、风速、太阳辐射、前1 h热负荷及前2 h热负荷作为预测模型的输入元素,通过机器学习进行热负荷预测。Idowu等人
以室外温度、历史热负荷、时间等参数为输入,通过机器学习进行了热负荷预测。Jihad等人
根据摩洛哥的供暖特征,建立热负荷神经网络预测模型。
2.2.5 水煎煮提取工艺正交试验 根据上述的药效筛选结果,对水煎煮提取工艺进行正交试验,以君药黄芪中黄芪甲苷含量(Y1)和固形物质量(Y2)为评价指标,并分别赋予权重系数0.6和0.4,计算综合评分值[Y,Yi=(X1i/X1max×0.6+X2i/X2max×0.4)×100],对影响煎煮的加水量(A)、煎煮时间(B)和煎煮次数(C)进行优选。因素与水平见表3。
刘鹏飞等人
在热负荷预测中将供水温度、日平均流量、日最低室外温度、日最高室外温度、日平均回水温度作为影响因素,得到预测精度更高且比较稳定的结论。Dagdougui等人
研究了包括时间、气象条件和历史数据在内的不同类型影响因素,得到室外温度是影响热负荷预测的主要气象条件之一,对预测结果有明显的影响。孟亚男等人
在基于室外温度的热负荷预测研究中提到,若将所有可能产生影响的因素全部考虑进去,得到的不一定是最好的预测模型。
一般情况下,大多数企业在生产环节上都需投入较多的人力、财力和物力,因此产品的生产过程是企业成本控制的重要环节。企业的生产成本主要包括材料成本、人力成本与制造费用,材料成本的控制需要避免不必要的浪费,人力成本的控制就需要加大流水线上的机械化程度,而制造费用的控制就需要减少公司在日常生产过程中因人为因素产生的成本,比如,水电费,设备维修费等。
当风送系统的风机转速在2000转/分,籽粒水分含量大于20%时,风道入口容易堵塞,需打开堵盖疏通,工作量较大,转速加大则出现嗑籽和撒籽现象。建议在收获前测定葵盘、籽粒含水率,选择籽粒水分含水率小于20%的地块进行收获。
本文采用相关性分析法、显著性检验法,对初始影响因素进行筛选。分别筛选出与热力站日供热量具有明显相关性、显著性水平高的影响因素。将初始影响因素、具有明显相关性的影响因素、显著性水平高的影响因素分别作为BP神经网络输入元素,建立热力站日供热量预测模型(以下简称预测模型)。采用相对误差、均方根误差和决定系数分别评价预测结果的可信程度、预测模型的稳定性、预测模型拟合效果。
2 预测流程
① 数据采集与处理。数据包括室外温度、室内温度、室外风速、供热量等,数据处理采用极大极小值法对原始数据进行归一化处理。
② 影响因素筛选。筛选方法分为相关性分析、显著性检验,分别筛选出与热力站日供热量具有明显相关性、显著性水平高的影响因素。为方便表述,将未经筛选的影响因素称为初始影响因素。
③ 预测模型建立。将初始影响因素、具有明显相关性的影响因素、显著性水平高的影响因素作为神经网络输入元素,分别建立预测模型。
,pre
——第
个热力站日供热量预测值,GJ
3 预测模型
3.1 预测模型
室外温度、室内温度、历史供热量、建筑类型以及围护结构等影响因素具有动态性且与热力站日供热量呈较大的非线性关系,而人工神经网络具有表达任意非线性映射的能力,能够对非线性系统进行建模
。
(3)本文经彩色多普勒超声检查的截瘫患者静脉血栓发生率与文献[5]报道一致。我们于治疗前后动态观察下肢静脉血栓,发现治疗后血栓缩小,血管再通率较治疗前提高,且截瘫患者康复时间也明显缩短。可以说,利用高频彩色多普勒超声动态观察截瘫患者下肢静脉血栓形成情况对指导临床治疗有重要意义。
3.2 影响因素筛选
采用相对误差、均方根误差和决定系数对预测模型进行评价,计算式分别为:
相关性分析是通过相关系数度量2个随机变量之间的相关程度。相关系数
的区间为[-1,1],当
∈[-1,0)时,表示负相关。当
∈(0,1]时,表示正相关。当
为0时,表示不相关。|
|越大,说明相关性越强。本文选取|
|>0.3作为影响因素与热力站日供热量具有明显相关性的判据。
② 显著性检验
室外最高温度、室外最低温度、室外日平均风速和历史供热量等因素均会对热力站日供热量产生影响。但研究表明,若把所有影响因素全部考虑进去,得到的不一定是最好的预测模型
。因此,采用逐步回归分析法分析影响因素的显著性水平
。将热力站日供热量作为因变量,影响因素作为自变量。当显著性水平
值小于0.05时,说明影响因素的显著性水平高。
BP神经网络包括输入层、隐含层、输出层,是一种具有3层或3层以上的多层神经网络,每一层都由若干个神经元组成
。采用LM(Levenberg-Marquardt)算法训练的BP神经网络(本文称为LM-BP神经网络),可以给出非线性最小化的数值解。LM算法结合了高斯-牛顿算法和梯度下降法的优点。重要的是,对于过参数化问题不敏感,能有效处理冗余参数问题,使代价函数陷入局部极小值的概率大大减小
。因此,本文采用LM-BP神经网络建立预测模型。
3.3 预测模型评价指标
① 相关性分析
1.4.2 组织样品 分娩之后,应当快速选取离母体面接近的胎盘脐带处组织2~4块,每块约1 cm3,需要注意的是取组织时应避开钙化点保存于-80 ℃和4%多聚甲醛固定。

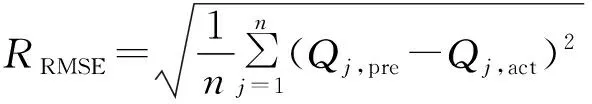
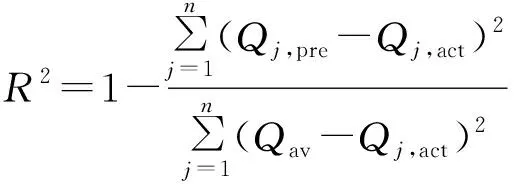
——热力站日供热量实际值的算术平均值,GJ
那天,她把缝纫机的针距调错了,自己根本没有意识到。当她把几百个袋子扎完,送到质检员陈建伟那里,还是陈建伟发现的问题。
④ 预测效果评价。依据预测效果评价指标,对不同预测模型进行评价。
天子射熊,诸侯射麋,卿大夫射虎豹,士射鹿豕,示服猛也。名布为侯,示射无道诸侯也。夫画布为熊、糜之象,名布为或,礼贵意象,示义取名也。土龙亦夫熊糜、布侯之类。[13](P923)
——均方根误差,GJ
——数据样本数量
——决定系数
,act
——第
个热力站日供热量实际值,GJ
式中
——相对误差
相对误差表征预测结果的可信性,以相对误差绝对值<5%的预测值比例达到90%及以上为预期。均方根误差表征预测值相对于实际值的平均偏差情况,可以用来评价预测模型的稳定性。均方根误差越小,预测模型的稳定性越高。决定系数取值范围为0~1,决定系数越大,表示预测模型拟合效果越好。
4 算例分析
4.1 数据采集与处理
以北京某热力站为研究对象,采集2019至2020年供暖期系统运行数据。采集数据包括室外温度、室内温度、室外风速、供热量等,每5 min采集1次。由于室内温度的有效性存在比较严重的问题,因此影响因素未考虑室内温度。对数据进行整理,得到室外日最高温度、室外日最低温度、室外日平均温度、室外日平均风速、日供热量等,共121组数据。对数据中的缺失值和异常值进行处理,部分缺失值采用均值插补法。不在最低和最高区间的异常数值删除,有条件的采用均值插补法填补,最终得到有效数据97组。采用极大极小值法,对有效数据进行归一化处理
。
4.2 影响因素筛选
初始影响因素与热力站日供热量的相关系数见表1。在进行显著性检验时,除相关性分析中的7个影响因素外,还加入了供暖室内设计温度,初始影响因素的显著性水平见表2。
由表1可知,与热力站日供热量具有明显相关性的影响因素有6个,按相关系数绝对值从大到小排序:前1 d供热量、室外日平均温度、室外日最低温度、前2 d供热量、前3 d供热量和室外日最高温度。室外日平均风速与热力站日供热量的相关性很小。由表2的显著性水平
值可知,与热力站日供热量显著相关的影响因素为室外日最高温度、室外日最低温度、前1 d供热量和供暖室内设计温度。
对于广大的英语学习者而言,提高写作能力是他们的追求,良好的英语写作水平象征着对英语这门语言的掌握程度。有些人汉语写作水平很高,倚马可待,可是一写到英语作文就语塞。要写好作文,不仅要有过硬的语言基本功,而且还需要具有审题、处理信息、驾驭文章结构、使用各种体裁和安排文章内容的能力。那么,我们如何才能提高自己的英语写作水平呢?


4.3 预测模型与结果分析
采用MATLAB软件建立预测模型,将表1中的7个初始影响因素作为预测模型A的输入元素,将具有明显相关性的6个影响因素作为预测模型B的输入元素,将显著性水平高的4个影响因素作为预测模型C的输入元素。3个预测模型隐含层的层数均为10层。随机选取70%的样本数据作为训练集,随机选取15%的样本数据作为验证集,剩余15%的样本数据作为测试集。
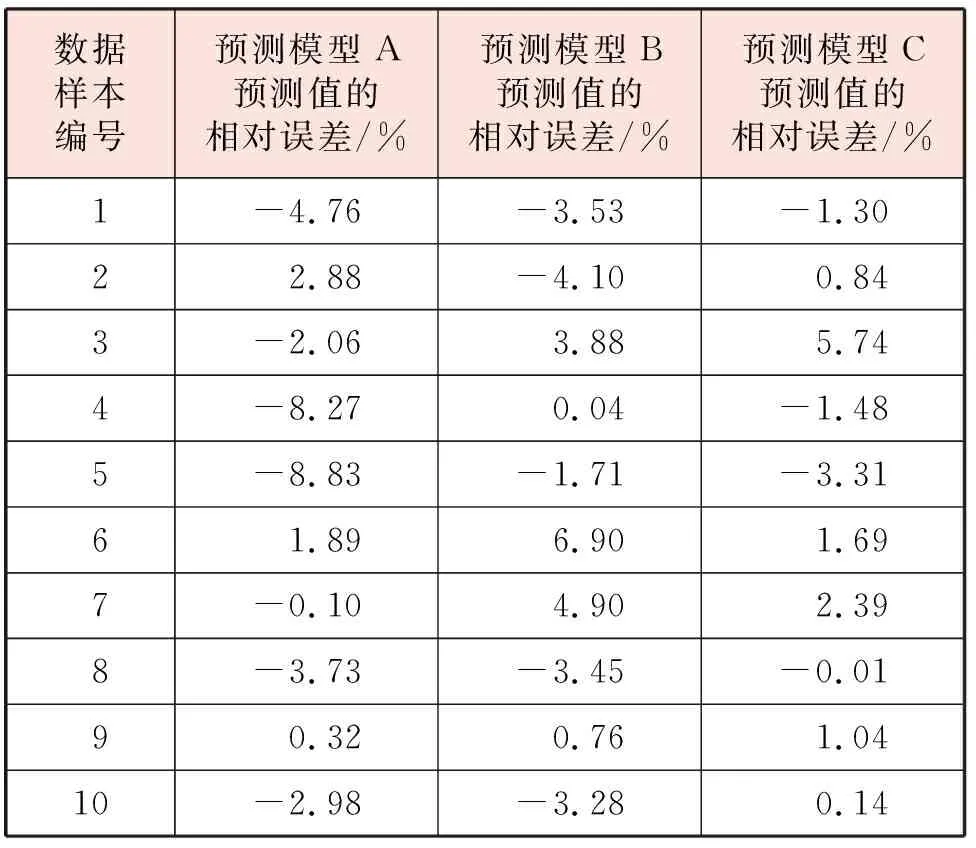
在验证集中随机选取10组样本数据,分别采用预测模型A~C对热力站日供热量进行预测,预测结果见表3。与实际值相比,预测模型A~C预测值的相对误差见表4。由表4可知,预测模型B、C实现了相对误差绝对值的预期(相对误差绝对值小于5%的比例达到90%及以上),预测模型A未实现预期。与预测模型A相比,预测模型B、C的预测结果更加可信。

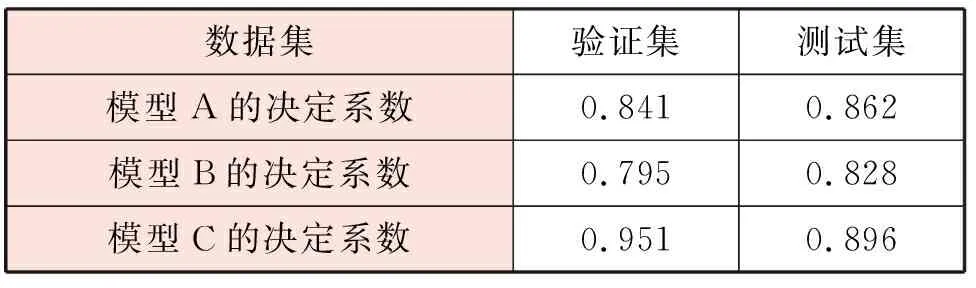
分别将验证集、测试集作为数据集,预测模型A~C的均方根误差、决定系数分别见表5、6。由表5可知,采用不同数据集时,预测模型C的均方根误差均最小,说明预测模型C的稳定性最高。由表6可知,采用不同数据集时,预测模型C的决定系数均最大,说明预测模型C的拟合效果最好。
预测模型C综合性能最好,以显著性水平高的影响因素作为输入元素的预测模型的预测结果可信性、稳定性、拟合效果最佳。

5 结论
预测模型C综合性能最好。以显著性水平高的影响因素作为输入元素的预测模型的预测结果可信性、稳定性、拟合效果最佳。
[ 1 ] 李锐,董妍,薛炜,等. 住宅区供热负荷预测研究[J]. 区域供热,2019(3):28-31,60.
[ 2 ] 单小伟. 智能楼宇中采用的节能控制技术原理分析[J]. 科技风,2020(10):9.
[ 3 ] 吴康福. 基于模糊神经网络的供热负荷预测模型构建[J]. 中阿科技论坛,2021(5):85-87.
[ 4 ] GIANNIOU P,LIU X,HELLER A,et al. Clustering-based analysis for residential district heating data[J]. Energy Conversion and Management,2018,165:840-850 .
[ 5 ] LIU Y F,HU X X,LUO X,et al. Identifying the most significant input parameters for predicting district heating load using an association rule algorithm[J]. Journal of Cleaner Production,2020,275:122984-1-10.
[ 6 ] 付波. 住宅区热力站负荷预测研究(硕士学位论文)[D]. 北京:北京建筑大学,2019:12-15.
[ 7 ] GEYSEN D,SOMER O D,JOHANSSON C,et al. Operational thermal load forecasting in district heating networks using machine learning and expert advice[J]. Energy & Buildings,2018,162:144-153.
[ 8 ] 朱冬雪,鹿世化,张帆,等. BP算法预测控制在供热系统中的节能应用[J]. 建筑热能通风空调,2020(4):50-52,65.
[ 9 ] 刘也. 基于小波神经网络与支持向量机的供热负荷预测方法研究(硕士学位论文)[D]. 吉林:东北电力大学,2020:32-35.
[10] IDOWU S,SAGUNA S,AHLUND C,et al. Applied machine learning: forecasting heat load in district heating system[J]. Energy & Buildings,2016,133:478-488.
[11] JIHAD A S,TAHIRI M. Forecasting the heating and cooling load of residential buildings by using a learning algorithm “gradient descent”,Morocco[J]. Case Studies in Thermal Engineering,2018,12:85-93.
[12] 刘鹏飞,李锐,王岩. 基于灰色神经网络模型的区域供热负荷预测研究[J]. 暖通空调,2019(5):124-128.
[13] DAGDOUGUI H,BAGHERI F,LE H,et al. Neural network model for short-term and very-short-term load forecasting in district buildings[J]. Energy & Buildings,2019,203:109408-1-8.
[14] 孟亚男,姚洁. 基于室外温度的供热负荷预测研究[J]. 吉林化工学院学报,2020(5):31-33.
[15] 潘世英,丁鑫,崔玥,等. MLP神经网络在供暖室内温度预测的应用[J]. 煤气与热力,2019(7):A40-A44.
[16] 于波,卢欣,李浩,等. 基于负荷预测的园区供热系统运行优化技术[J]. 电力建设,2017(12):77-86.
[17] 胡江涛,王新轲,刘罡. 人工神经网络预测供热系统供水温度[J]. 煤气与热力,2019(3):A06-A11.
[18] OUAMMI A,ZEJLI D,DAGDOUGUI H,et al. Artificial neural network analysis of moroccan solar potential[J]. Renewable and Sustainable Energy Reviews,2012,16:4876-4889.
[19] 张鸿燕,耿征. Levenberg-Marquardt算法的一种新解释[J]. 计算机工程与应用,2009(19):5-8.
[20] 姚健,周伟国,张中秀. 人工神经网络法燃气日负荷预测输入变量选取[J]. 煤气与热力,2010(1):B28-B30.
[21] ZHAO Y,ZHANG C B,ZHANG Y W,et al. A review of data mining technologies in building energy systems: load prediction,pattern identification,fault detection and diagnosis[J]. Energy and Built Environment,2020(2):149-164.
