断层与平行隧道空间位置关系对涌水量的影响研究

傅鹤林，安鹏涛，成国文，李鲒，陈龙，余小辉

(1.中南大学 土木工程学院，湖南 长沙 410075；2.中南大学 高速铁路建造技术国家工程试验室，湖南 长沙 410075；3.广东省南粤交通投资建设有限公司，广东 广州 510101)

隧道位于富水断层破碎带时，地下水在其整个建设过程及运营期都不断地涌入隧道，对结构及生态环境产生极大的挑战[1-2]。综合考虑结构安全及生态环境因素，富水断层区山岭隧道多采用“以堵为主，限量排放”即“堵水限排”的防排水设计准则[3-4]。此时，研究断层对隧道涌水量的影响具有重要的理论意义和工程应用价值。张顶立等[5-13]基于渗流力学理论及质量守恒定律，分析了半无限平面内深埋隧道附近渗流场对注浆参数变化的敏感性，为注浆圈的设计提供了理论基础。针对富水断层构造区隧道涌水量计算的问题，WANG等[13]利用势函数叠加的方法推导了隧道揭露断层破碎时掌子面涌水量计算表达式；方勇等[14-15]基于数值模拟方法，对复杂构造区隧道的突涌水特征进行了模拟；张庆松等[16-19]利用断层破碎带隧道突水突泥模型试验系统，揭示了揭露断层后的隧道围岩渗流压力、应力应变、位移及涌出物等物理量的变化规律；傅鹤林等[20]通过将隧道横断面内具有一定倾角的断层等效为竖直倾角，建立了断层附近的隧道渗流简化模型，推导了隧道涌水量计算公式。学者多通过数值模拟及模型试验手段分析断层对隧道涌水量的影响，理论分析时多将断层进行等效，而鲜有系统分析断层与平行隧道位置关系对涌水量的影响。基于此，利用反映法将有界含水层转变为无界问题，构建含断层的深埋平行隧道涌水简化计算模型，基于地下水力学理论、达西定律及线性叠加原理推导涌水量计算公式，并进行退化验证，再对相关参数进行敏感性分析，最后通过在建隧道对构建模型的合理性及公式推导的正确性进一步检验。

1 理论分析与基本假定

1.1 反映法原理

反映法：把有界含水层用映射原理转变为无界问题，再通过叠加原理求解。反映法基本规律为[21]：

1)虚构井与实际井的位置对称；

2)虚构井的流量与实际井相等；

3)虚构井的性质(输水与注水)取决于边界的性质：对直线隔水边界，虚构井的性质与实际井相同；对直线定水头边界，则相反。

1.2 叠加原理

系统叠加原理认为在线性系统中，由同一原因形成的物理量，其状态标量场按代数和原则叠加，其矢量场按矢量求和叠加[22]。

1.3 计算模型及基本假定

建立半无限平面内双孔平行隧道的渗流模型，如图1所示。图1中，r01,re1,rg1分别为隧道1支护结构内缘半径、支护结构外缘半径及注浆圈外径；r02,re2,rg2分别为隧道2支护结构内缘半径、支护结构外缘半径及注浆圈外径；平行隧道水平与竖直间距分别为b与d。

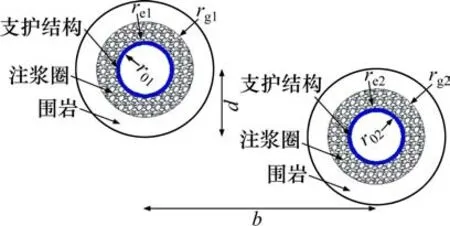
图1 半无限平面内双孔平行隧道渗流计算模型Fig.1 Seepage calculation model of double hole parallel tunnel in semi-infinite plane

考虑实际工况及方便问题解答，作如下假定[23]：

1)围岩与各结构均质且各向同性；

2)隧道处于稳定渗流状态；

3)渗流服从达西定律；

4)隧道为大埋深。

2 涌水量及渗水压力计算与验证

利用反映法，将双孔隧道渗流场转化为无限渗流场下4个单孔隧道的叠加问题，如图2所示。图2中：断层倾角为β；距断层较近的隧道与断层水平距离为L；点M为渗流场中任意点，R1,R2,R3及R4分别为点M至各隧道中心点的距离。

由图2可知，各隧道中心坐标计算表达式为

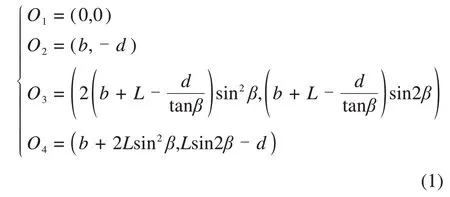
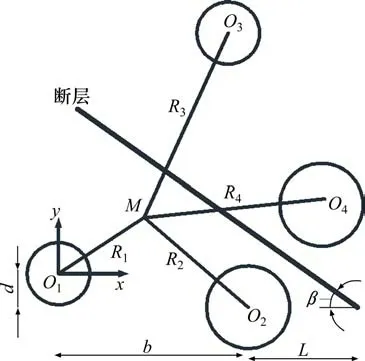
图2 含断层的双孔平行隧道简化计算模型Fig.2 Simplified calculation model of double-hole parallel tunnel with fault

根据假定，水流速度与水力坡度满足达西定律，表达式为

式(2)中：v为渗流速度；k为介质渗透系数；i为水力坡度。

根据渗流力学原理，无限平面内单孔隧道稳定径向渗流连续性方程极坐标表达式为[24]

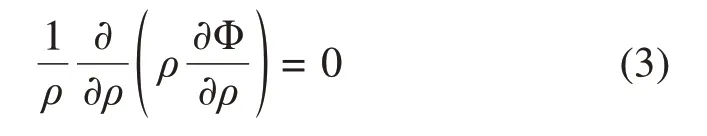
式(3)中：ρ为计算点至隧道中心的距离；Φ为无限平面内计算点的渗流场水头势函数。

假定某断面的流量为Q，得

式(4)的通解表达式为

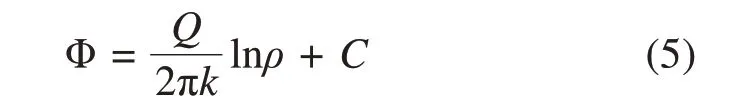
式中：C为待定常数，其值由边界条件确定。

当无限平面内4个隧道(两虚井，两实井)均达到稳定渗流时，平面内任意一点水头势函数根据势的叠加原理确定，计算式为

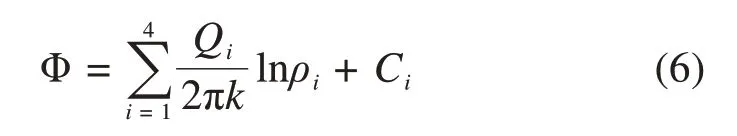
式中：Qi为第i个隧道的涌水量；Ci为常数。

假定围岩渗透系数为kr，渗流稳定时隧道O1与O2涌水量分别为Q1与Q2，则M点水头势函数表达式为

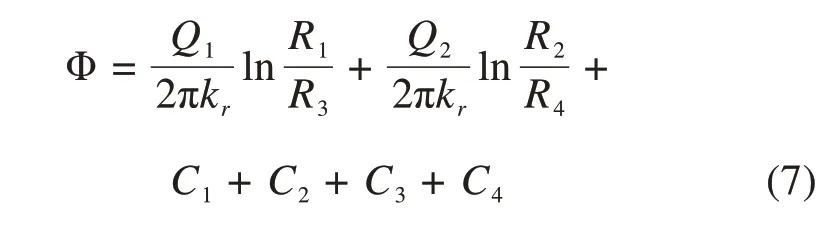
若点M位于断层处，即满足

假定断层为定水头边界，水头高度恒为H，将式(8)代入(7)，可得

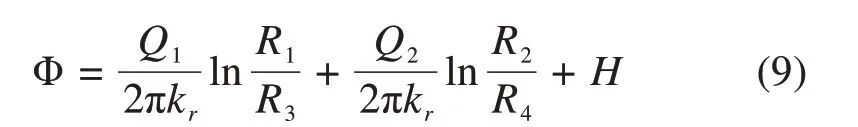
2.1 涌水量计算

隧道施工至断层影响区时，为保护地下水资源及结构稳定性需在隧道开挖前进行帷幕注浆，使注浆形成的止水圈成为堵水屏障，同时分担部分水压力，从而提高隧道施工及运营期安全性。

若点M位于隧道1的注浆圈外缘，由图2及式(1)可知

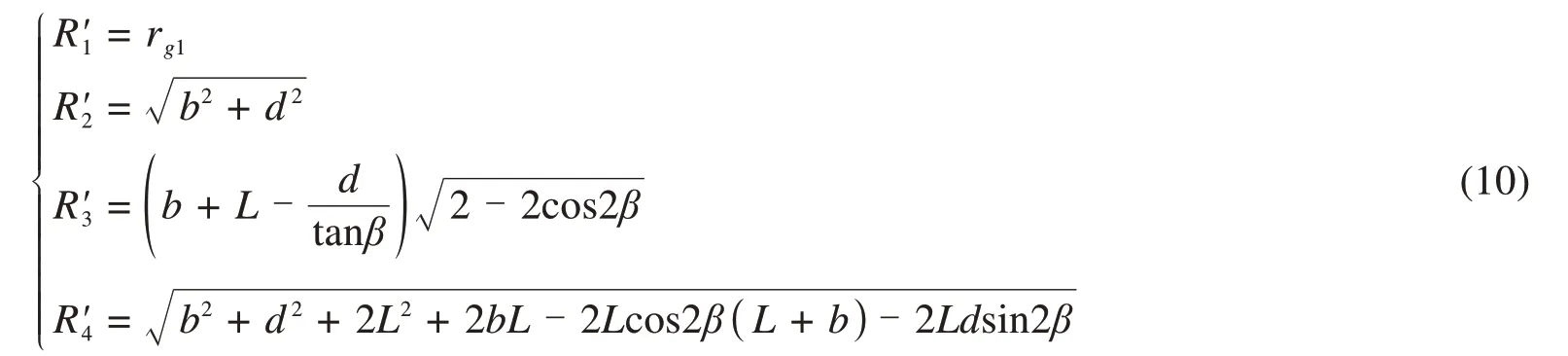
假定隧道1注浆圈外缘水头高度为hg1，其表达式为

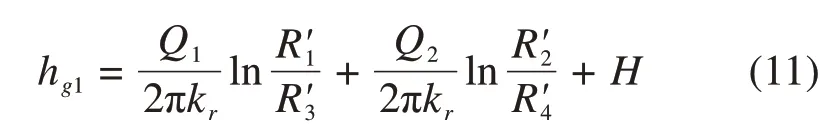
若点M位于隧道2的注浆圈外缘，由图2及式(1)可知

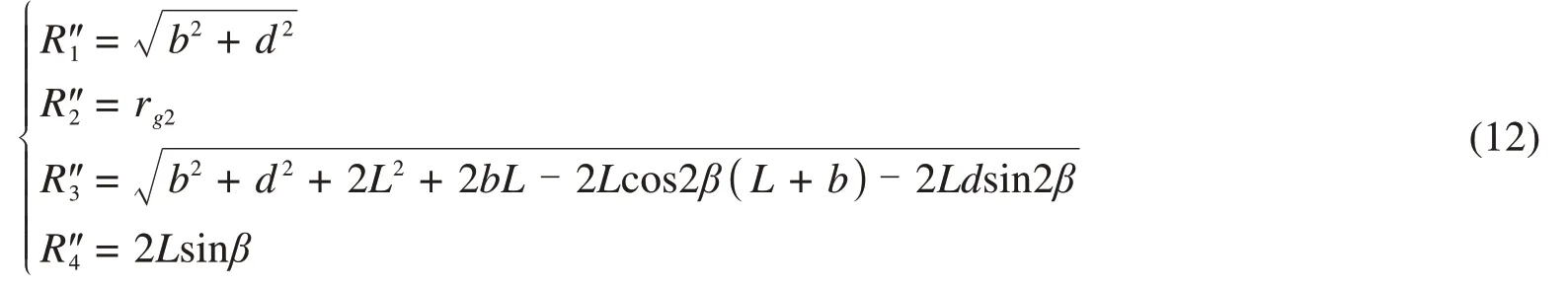
假定隧道2注浆圈外缘水头高度为hg2，其表达式为

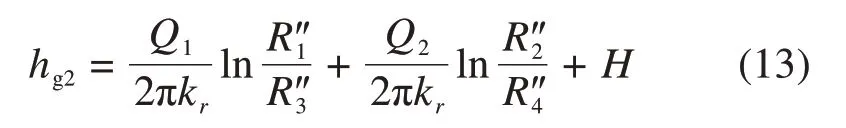
深埋隧道渗流稳定时，据地下水力学理论[25]

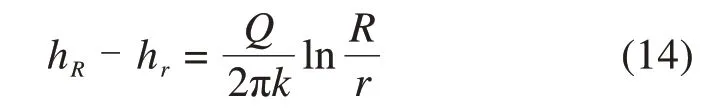
式中：h R及hr为距计算区中心距离为R与r位置处的水头高度。

假定隧道1注浆圈内缘与支护结构内缘水头高度分别为he1，h01；隧道2注浆圈内缘与支护结构内缘水头高度分别为he2，h02。由式(14)可知

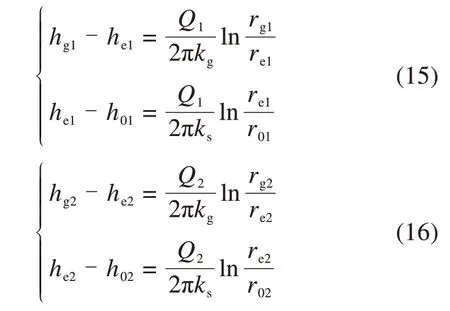
联立式(11)、式(13)及式(15)～(16)，求得涌水量计算表达式为

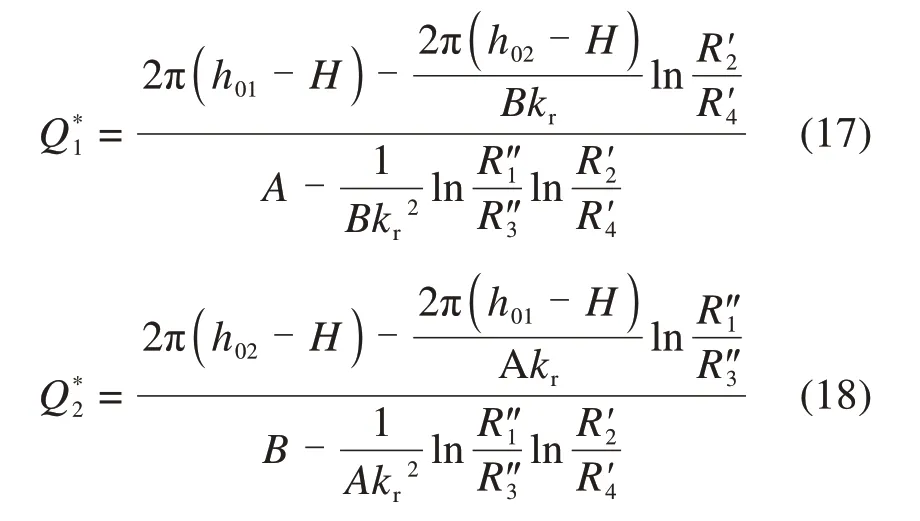
式(17)和(18)中：A与B满足如下表达式

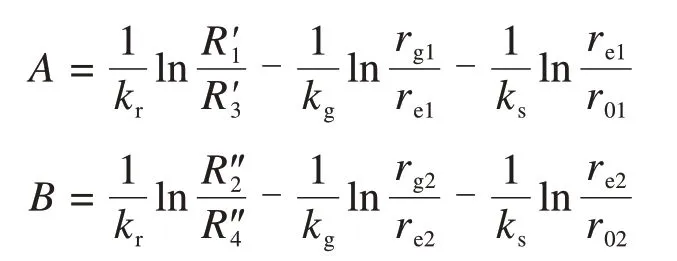
2.2 渗水压力计算

联立式(15)与(17)，求得隧道1支护结构外缘与注浆圈外缘水头高度表达式为

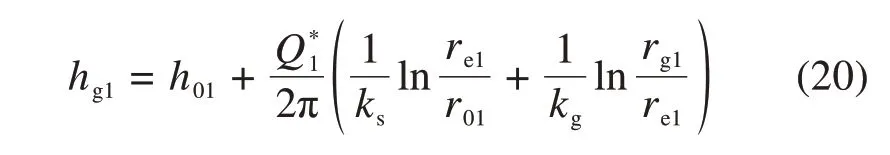
联立式(16)与(18)，求得隧道2支护结构外缘与注浆圈外缘水头高度表达式为

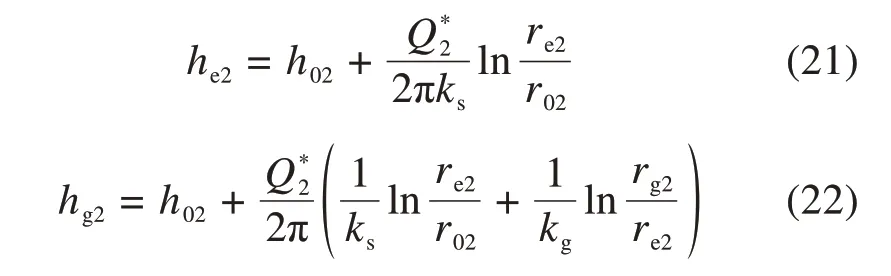
2.3 退化分析

忽略断层及隧道2的影响，则r02=re2=此时式(17)退化为

式(23)与文献[26]计算结果相同，表明式(17)可退化为不考虑平行隧道的干扰及断层的影响时单孔隧道的涌水量求解计算公式。同时文献[27]在计算隧道毛洞涌水量时具有较高的准确度，忽略毛洞内水头，不考虑注浆加固且未施作衬砌时，此时h01=0，r g=r1=r0，式(17)进一步退化为

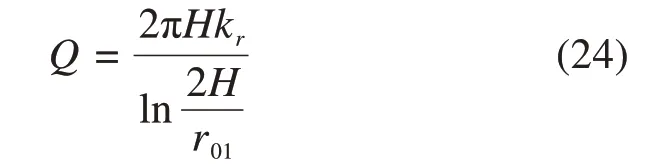
式(24)为古德曼方程计算毛洞涌水量的解析公式。

即公式(17)若不考虑断层及平行隧道的干扰时，可退化到文献[26]所推导的渗流稳定时隧道涌水量计算公式；不考虑注浆圈与衬砌的堵水作用时，本文所推导的公式与文献[26]所建立的公式均可退化到文献[27]所推导的开挖隧道后最大涌水量计算公式。一定程度上验证了本文构建模型的合理性及公式推导的正确性。

3 特征参数分析

3.1 断层与隧道位置关系对涌水的影响分析

平行隧道支护结构内缘半径均为6 m，支护结构外缘半径均为6.6 m，注浆圈外缘半径均为10.6 m；平行隧道水平距离b为50 m，竖直距离d为0；断层处水头高度为350 m；围岩、注浆圈与支护结构渗透系数分别为10-6m/s，2.5×10-8m/s及2.5×10-9m/s。假定平行隧道支护结构内缘水头高度均为0，据式(17)～(18)分析断层与隧道位置关系对平行隧道涌水量的影响，其中平行隧道1及2涌水量分别为Q*1及Q*2，绘制曲线如图3所示。

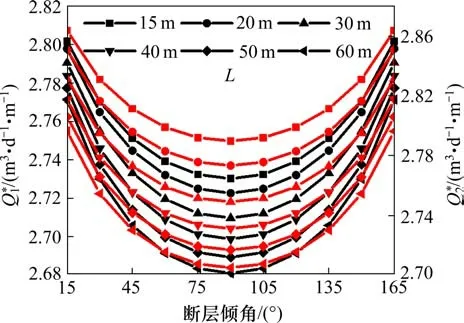
图3 断层与隧道位置关系对涌水量的影响Fig.3 Influence of the position relationship between the fault and the tunnel on the water inflow

图3表明，渗流稳定时，当断层倾角为90°，隧道1与2涌水量均最小；两隧道涌水量随断层与隧道2水平距离的增大而不断减小。分析认为，当断层倾角为90°时，两隧道与断层的垂直距离均达到最大，渗流稳定时涌水量受断层影响较小，故此时涌水量最小。同时，由于隧道2距断层较近，故渗流稳定时隧道1涌水量小于隧道2涌水量。

3.2 平行隧道空间位置关系对涌水的影响分析

假定断层与隧道2水平距离L为30 m，围岩与隧道结构空间几何参数及渗透系数与3.1节相同，分析断层倾角β分别为90°及60°时平行隧道空间位置关系对隧道涌水量的影响，如图4所示。

图4显示，隧道2稳定涌水量随隧道1的远离而增大。究其原因，随隧道1的远离，隧道1与2之间的相互干扰逐渐降低，故涌水量逐渐减小。

图4 平行隧道空间位置关系对涌水量的影响Fig.4 Influence of the spatial position of parallel tunnels on water inflow

隧道1涌水量受隧道1与2的距离而变化，但关系较为复杂。当隧道1与2的竖直距离较小时：假定平行隧道竖直间距较小，当平行隧道水平间距较小时，平行隧道间的干扰对隧道1的涌水影响较大；当平行隧道水平间距较大时，断层对隧道1涌水影响较大。

同时，与上节结论相似，断层倾角为60°时两隧道涌水量均比断层倾角为90°的大。

4 工程案例

4.1 工程背景

鸿图隧道为双洞单线工程，左洞起止桩号为ZK89+380～ZK95+716共6 336 m，右洞起止桩号为K89+405～K95+742共6 337 m。地面标高345～1 060 m，隧道底部设计标高239～344 m，最大埋深约739 m。2019年4月23日，右线隧道掌子面开挖至K91+169时，掌子面出水量增加，经现场估算出水量约1 400 m3/h，涌水压力高达4.8 MPa。现场涌水情况如图5所示。

图5 隧道涌水Fig.5 Water gushing in tunnels

为检验帷幕注浆效果，在相应里程桩号初期支护内埋设智能弦式数码渗压计。渗压计量程为1.0 MPa，灵敏度为0.001 MPa，现场埋设与测量如图6所示。

图6 现场安装与测量Fig.6 Field installation and measurement

4.2 参数选取

目前对非圆形断面隧道一般采用保角变换将其映射为圆形[28]，但复变函数求解过程复杂，且由于复变函数的固有问题[29]，常采用等代圆法将真实隧道断面简化为圆形断面，此法对曲墙式隧道引起的误差一般在可接受的范围内[30]。文献[31]对等代圆半径进行了分析，本文取隧道断面外接圆半径为等代圆半径，表达式为

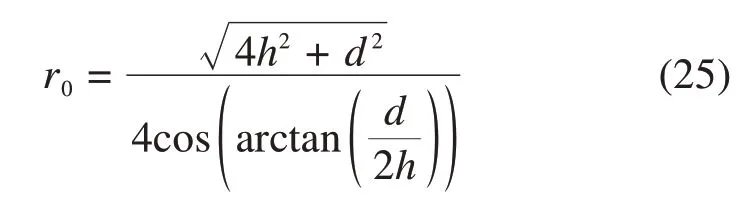
式中：r0为原隧道做等代圆处理后的半径；d为原隧道的断面跨度；h为原隧道的断面高度。

计算得等代圆半径r0为6.2 m。初期支护与二次衬砌综合考虑为80 cm。为验证本文解的正确性，选取鸿图隧道某试验段进行分析，其中隧道与断层位置关系如图7所示。

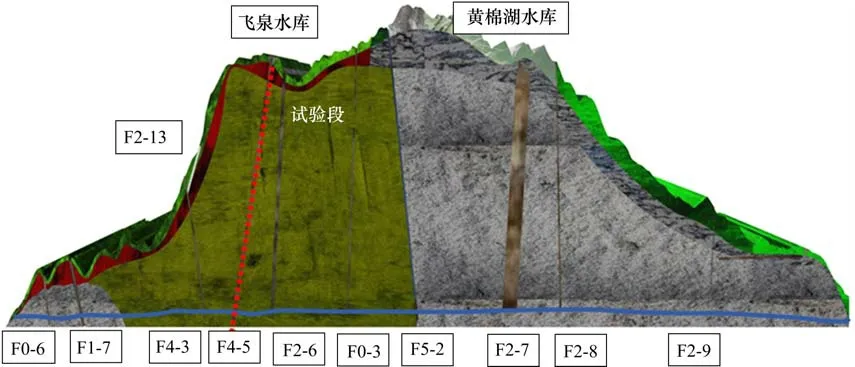
图7 隧道与断层位置关系Fig.7 Relationship between the tunnel and the fault position

为确定试验段地下水与地表水连通关系，现场取水测试，如图8所示。

图8 取样分析Fig.8 Sampling analysis

结合设计院与现场测试及施工经验，各参数取值如表1所示，其中支护结构渗透系数综合考虑了环向与纵向排水管作用，其取值参考文献[32]的计算方法。

为验证构建涌水计算模型的合理性及公式推导的正确性，现场测量试验段横向排水管的水量，如图9所示。

图9 涌水量测量Fig.9 Water inflow measurement

4.3 结果分析

据式(17)～(18)，利用表1数据，计算得平行隧道1与2涌水量分别为2.6 m3/(d∙m)及2.64 m3/(d∙m)，现场实测涌水量分别为2.79 m3/(d∙m)与2.95 m3/(d∙m)，理论计算与实测误差分别为6.8%及10.5%。

表1 参数取值Table 1 Parameter value

本文理论解与实测值差距较小，在可接受范围内，一定程度上验证了本文构建的含断层的平行隧道涌水简化计算模型的合理性及公式推导的正确性。预测误差主要为等代圆的近似代替及断层附近渗透系数的离散型导致。

5 结论

1)构建了含断层的深埋平行隧道涌水简化计算模型，推导了涌水量及外水压力计算公式，并进行了退化分析。

2)渗流稳定时，断层倾角为90°时对平行隧道涌水影响最小。

3)探究断层与平行隧道空间位置关系对涌水量的影响研究时，应考虑平行隧道的干扰。

4)通过算例分析，本文解与实测数据误差在可接受范围内，验证了构建模型的合理性及公式推导的正确性。