加劲梁带外伸跨的大跨度悬索桥动力特性分析

祝志文，姜子涵

(汕头大学 土木与环境工程系，广东 汕头 515063)

悬索桥是指以通过主塔悬挂并锚固于桥两端或两岸的缆索作为上部结构主要承重构件的桥梁[1]，是跨越能力最大的桥梁结构之一。大跨度悬索桥的竖向刚度主要来自主缆的重力刚度，而加劲梁刚度对结构整体刚度贡献有限[2]。挠度理论揭示了对于跨度超过1 000 m的悬索桥，结构整体竖向刚度主要来源于主缆[3]。挠度理论作为悬索桥解析计算经典理论之一，最先被用于单跨悬索桥的静力计算[4]。大跨度悬索桥属于柔性结构体系，结构特性决定其具有独特的动力特性[5-6]，在悬索桥受到风荷载或者车辆移动荷载等动力作用下，桥梁会有明显的动力响应。目前很多学者对于悬索桥的动力特性做了相关研究[7−9]，动力特性分析对于桥梁抗震抗风有重要的参考价值。早期的悬索桥多为简支体系，而连续体系有利于桥梁抗风和行车平顺性，已成为现代大跨度悬索桥的发展趋势。从静力学角度来看，半漂浮体系的竖向支承作为一个硬点，有悖于连续体系的“柔和”，而全漂浮体系恰恰迎合了这一特点[10]。考虑经济性，国内大跨度悬索桥多采用传统的单跨两铰体系。已有计算资料和工程实践表明，这种结构体系在梁端会产生较大的转角和纵横向位移，可能影响端支座等结构的耐久性[11]。为改善这种结构体系的静动力性能，可考虑将加劲梁在桥塔处向外延伸一跨，即加劲梁带外伸跨的单跨悬吊体系。外伸跨的设置在自锚式悬索桥中较为普遍，而且在地锚式悬索桥中也有应用。张东[11]以下津井獭户大桥为研究对象，研究设外伸跨对结构横向刚度和竖向刚度的影响。结果表明，支承体系从单跨悬吊带外伸跨变为单跨两铰体系，挠度和梁端转角已远超过铁路悬索桥对刚度限值的要求，单跨悬吊带外伸跨体系的列车走行性优于单跨两铰体系。王志诚等[12]通过对设置70 m外伸跨的自锚式悬索桥进行研究，得出设与不设外伸跨对结构的受力性能可能产生根本性的影响，外伸跨主要起压重和减小边跨恒载内力的作用，可较大幅度提高结构的整体竖向刚度。唐冕[13]以三汉矶湘江大桥为背景，通过改变外伸跨长度来研究其对结构刚度和内力的影响。研究得出，自锚式悬索桥随着外伸跨长度增加，结构的整体刚度要减小，外伸跨不仅可以起到压重的作用，还可以有内力重分布的作用，合适的伸跨长度对减小结构的竖向挠度非常有效。到目前为止，尽管很多学者针对大跨度悬索桥静动力特性做了大量研究[14−17]，但很少有针对集单跨悬吊、带外伸跨、连续漂浮等特征于一身的大跨度地锚式悬索桥进行动力特性分析，且对于不同加劲梁布置形式与约束体系的研究较少。此外，前述对加劲梁带外伸跨的研究多为自锚式悬索桥，或者中等跨度地锚式悬索桥，而对主跨超千米的地锚式悬索桥研究的例子较少。鉴于此，本文以国内某主跨1 098 m+50 m外伸跨的单跨悬吊悬索桥设计方案为研究对象，其主梁为连续全漂浮体系，通过有限元软件建模，对其进行动力特性分析。通过将其与传统单跨两铰悬索桥及设置悬吊外伸跨悬索桥进行对比，研究不同的加劲梁外伸跨布置形式对悬索桥动力特性及刚度的影响。同时，研究了加劲梁约束体系对该悬索桥动力特性及刚度的影响。评价外伸跨对悬索桥结构刚度的影响，并为悬索桥的优化设计提供理论依据，指导桥梁工程实践。

1 工程背景

国内某主跨1 098 m的单跨悬吊悬索桥，主梁为正交异性钢桥面板钢箱梁结构，主跨钢箱梁往两侧各伸出50 m外伸跨。主缆跨径布置为251 m+1 098 m+251 m，垂跨比为1/10。主缆在塔顶、锚碇处横向间距分别为33.8 m和36.2 m，吊索顺桥向标准间距为12.8 m。主梁在2个过渡墩处设置竖向支座、横向抗风支座，在桥塔处放开无约束。桥塔设置上、下2道横梁，总高度174 m。钢箱梁全宽38.6 m，箱梁外侧设置宽2.8 m检修道。主梁共8种类型，96个梁段图，标准梁段长12.8 m，设置4道实腹式横隔板，间距3.2 m。图1为该悬索桥概况。

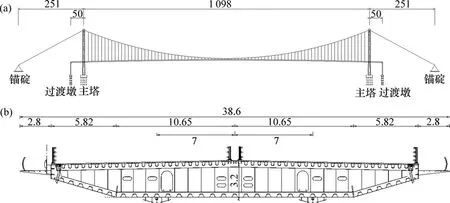
图1 悬索桥概况Fig.1 Suspension bridge overview

2 有限元模型

采用有限元软件ANSYS建立计算模型，吊索、主缆采用Link10单元模拟，初始轴力通过单元初应变模拟；主塔、主梁等采用Beam4单元模拟，主梁采用单梁式力学模型，它把桥面系的竖向刚度、横向刚度、扭转刚度及平动质量、转动惯量都集中在中间节点上，通过主从约束同吊索形成鱼骨型；用Mass21单元模拟1期和2期恒载的质量及质量矩。该悬索桥加劲梁体系为带外伸跨的单跨悬吊体系，全桥约束系统布置如下：全漂浮体系，主梁与桥塔之间不设约束；忽略桩-土结构相互作用的影响，桥塔在承台处固结；主缆在塔顶主索鞍中心处固结；边跨主缆锚固于地锚上；主梁梁端在竖向、横桥向、绕顺桥向转动的自由度与过渡墩相应节点采用主从约束。全桥有限元模型和约束系统布置如图2所示。

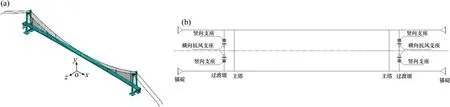
图2 全桥有限元模型和约束系统布置Fig.2 Full bridge finite element model and restraint system layout

3 动力特性分析

采用有限元软件的模态分析模块进行动力特性分析，模态分析能为桥梁抗震设计、抗风设计以及车桥耦合振动研究提供参考。模态分析是带有初应力的模态分析，考虑缆索张力对悬索桥动力特性的影响。大跨度悬索桥的模态分析分2步进行：首先是静力分析得到悬索桥的初始平衡构型，模态分析始于静力初始平衡构型。处于初始平衡构型的桥梁，其构件内部存在很大的初应力，这种初应力状态应反映在有限元模型中；然后是基于初始平衡构型的模态分析，即有初应力的模态分析。通过模态分析得到该加劲梁带外伸跨的单跨悬吊悬索桥的前20阶振型，主要模态振型与频率见表1，表2为大跨度悬索桥第1阶模态汇总，典型振型图如图3所示。

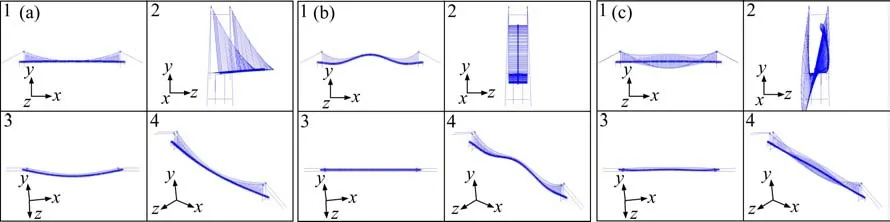
图3 典型振型图Fig.3 Typical vibration shape chart

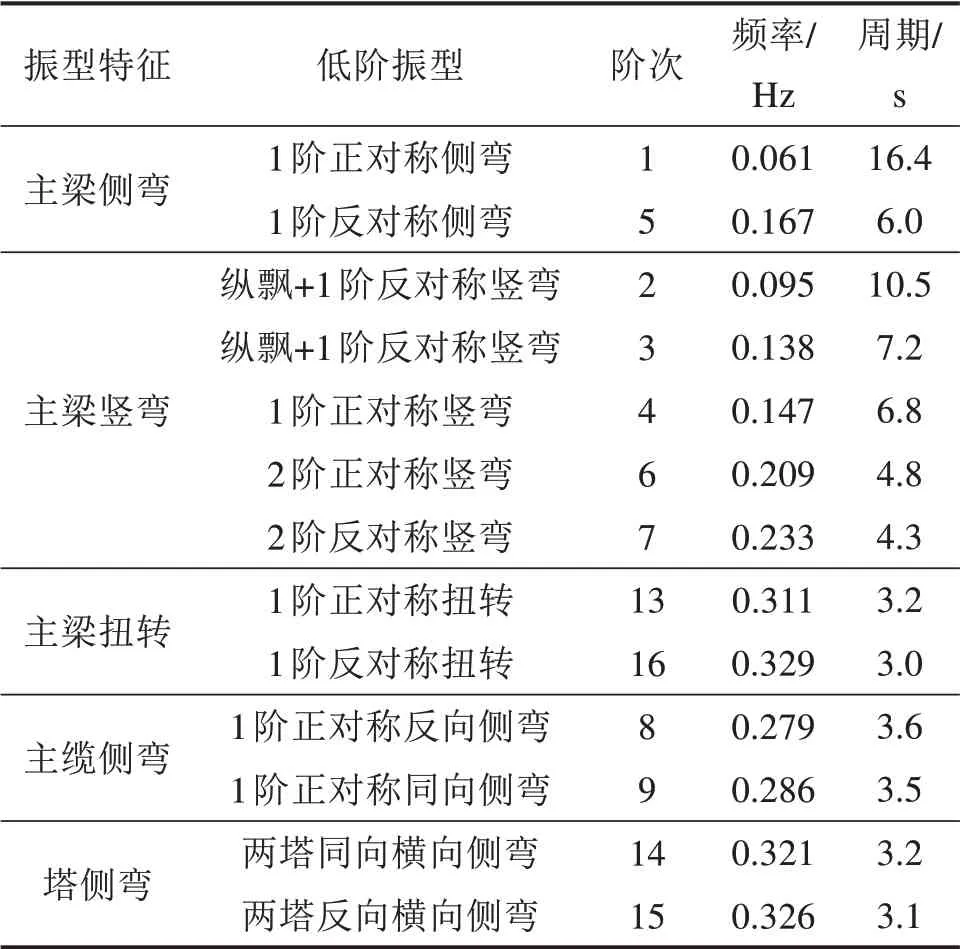
表1 主要模态振型与频率Table 1 Main mode shape and frequency

分析表1结果，可以得出以下结论：

1)该悬索桥基频为0.061 Hz，自振周期为16.4 s，体现了大跨度悬索桥长周期柔性结构特点。表2[18−19]列出了同类大跨度悬索桥第1阶模态汇总结果。该主跨1 098 m的悬索桥，自振周期刚好位于主跨1 385 m的江阴长江公路大桥(19.6 s)和主跨960 m的宜昌长江公路大桥(14.2 s)之间，基本周期符合规律。

表2 大跨度悬索桥第1阶模态汇总Table 2 Summary of first-order modes of large-span suspension bridges

2)由于该结构为全漂浮体系，沿纵桥向的自由度放松，虽会出现纵飘现象但并不是在第1阶出现。第2～3阶振型均出现主梁纵飘，说明悬索桥的纵向刚度相对较弱，体现了缆索结构体系悬索桥柔性的特点。第2阶振动频率为0.095 Hz，对应振型为1阶反对称竖弯伴随纵飘振型，符合大跨悬索桥柔性结构的一般规律[20]。

3)由横向振型可知，第1阶振型为主梁1阶正对称侧弯，基频为横向振型，说明其横向刚度相对较小；由竖向振型可知，竖向振动为主的振型从第2阶出现且频率较低，前多阶模态存在较多桥面竖弯振型，说明此带外伸跨悬索桥的竖向抗弯刚度相对较小；由于该带外伸跨悬索桥1阶扭弯比为2.1(正对称)和3.5(反对称)，就气动稳定性而言可能有较好的抗风稳定性。

4)悬索桥模态最先出现主梁主导的振动，随后出现主缆的振动，主塔的振动出现得最晚。该桥前7阶振型均以主梁振动为主，其中侧弯和竖弯出现较早，扭转出现较晚，说明该悬索桥抗扭刚度相对较好。桥塔横桥向振动出现较晚，且与主缆振动耦合在一起，而桥塔顺桥向振动由于缆索的约束而没有出现。

4 加劲梁外伸跨布置形式研究

悬索桥一般采用传统单跨两铰体系，当跨度超过千米后，尚不清楚仍设计50 m外伸跨是否可以改善结构性能。为评价此带外伸跨单跨悬吊体系合理性，现研究不同加劲梁外伸跨布置形式对结构动力特性影响，分别比较3种加劲梁外伸跨布置形式：设置外伸跨；不设置外伸跨；设置悬吊外伸跨。模型Ⅰ为该带外伸跨单跨悬吊体系，另外建立模型Ⅱ和模型Ⅲ有限元模型。3种加劲梁外伸跨布置形式如图4所示。

模型Ⅰ：加劲梁带外伸跨的单跨悬吊体系(以下简称单跨带外伸跨体系)(50 m+1 098 m+50 m)。

模型Ⅱ：传统的单跨两铰加劲梁体系(以下简称传统单跨两铰体系)(1 098 m)。

模型Ⅲ：加劲梁带外伸跨的3跨连续悬吊体系(以下简称3跨连续体系)(50 m+1 098 m+50 m)。

4.1 有无设置外伸跨的对比

现研究设置加劲梁外伸跨对结构动力特性影响，比较模型Ⅰ和模型Ⅱ2种模型。模型Ⅰ为单跨带外伸跨体系，模型Ⅱ为传统单跨两铰体系，如图4所示。对模型Ⅱ进行动力特性分析，并将前20阶主要低阶振型与模型Ⅰ进行对比分析。表3为模型Ⅰ和模型Ⅱ的振型频率值对比。

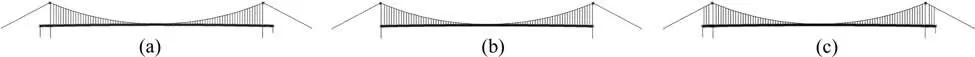
图4 3种加劲梁外伸跨布置形式Fig.4 Three layouts of extended spans of stiffening girders

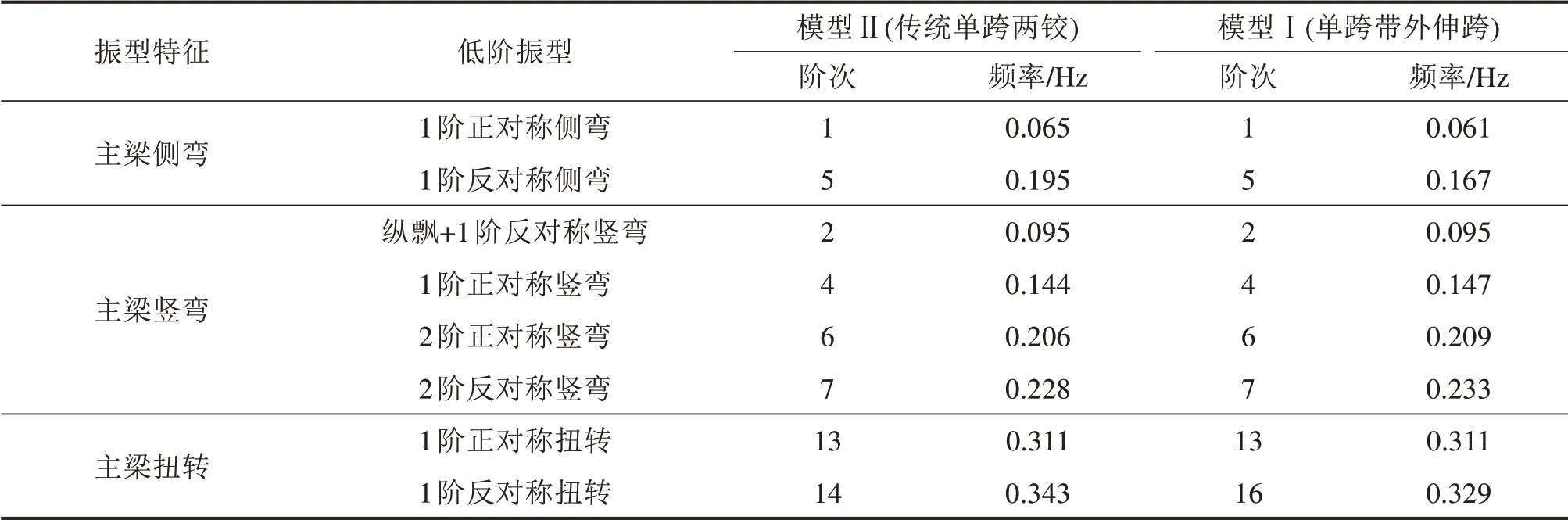
表3 模型Ⅰ和模型Ⅱ的振型频率值对比Table 3 Comparison of mode shape frequency value of model I and model II

根据表3可知，2种体系在纵向放松的约束体系下，纵飘振型都出现在第2阶，第1阶振型都为主梁1阶正对称侧弯。分析侧弯振型可知，2种模型主梁由于只有梁端约束且约束条件类似，设外伸跨会增加纵桥向长度，从而导致主梁横向刚度略有减小，其中1阶正对称侧弯频率减少了6.2%；分析竖弯振型可知，单跨带外伸跨体系竖弯频率整体高于传统单跨两铰体系，其中1阶、2阶正对称竖弯频率分别提高了2.1%和1.5%，表明设置外伸跨略微提升了主梁的竖向刚度；对于扭转振型，1阶正对称扭转频率无变化，说明有无外伸跨对扭转振动的影响较小。由此可见，增设外伸跨可一定程度上提升传统单跨两铰悬索桥主梁的竖向刚度。因此对于单跨悬吊的大跨度悬索桥，适宜采用单跨带外伸跨的加劲梁体系。

4.2 外伸跨有无设置吊索的对比

在带外伸跨的单跨悬吊体系(模型Ⅰ)基础上，在外伸跨增设吊索，加劲梁由单跨悬吊变为3跨连续悬吊(模型Ⅲ)，如图4所示。为研究外伸跨有无设吊索对结构动力特性的影响，现比较模型Ⅰ和模型Ⅲ两种模型。模型Ⅰ为单跨带外伸跨体系，模型Ⅲ为3跨连续体系。对模型Ⅲ进行动力特性分析，并将前20阶主要低阶振型和模型Ⅰ进行对比分析。表4为模型Ⅰ和模型Ⅲ的振型频率值对比。

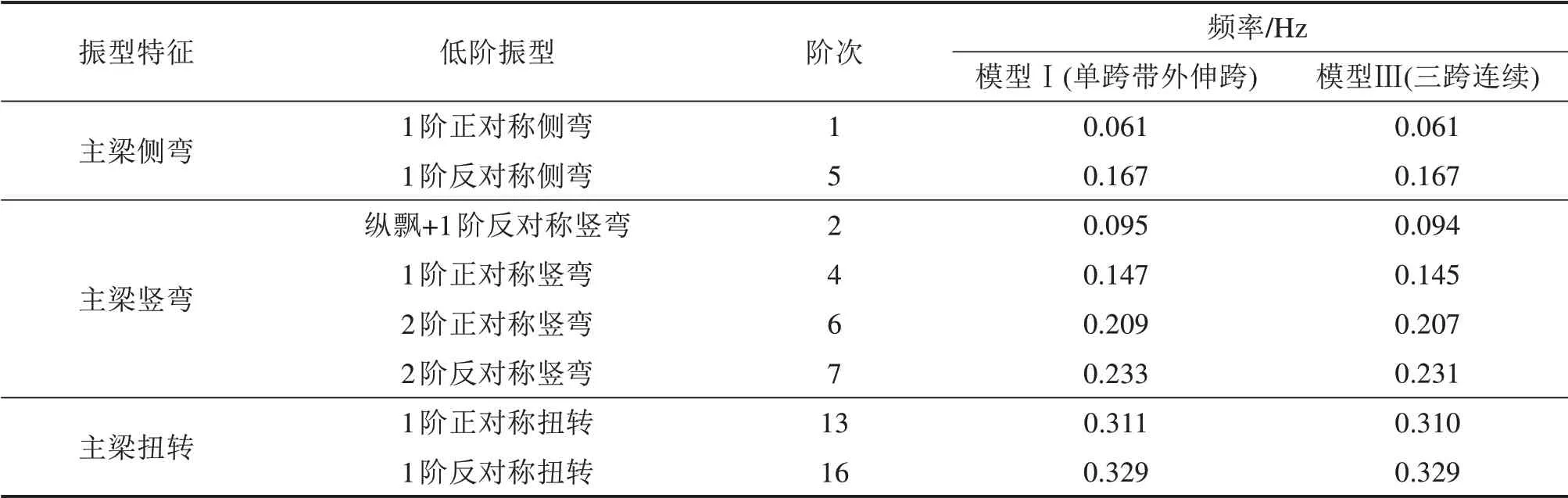
表4 模型Ⅰ和模型Ⅲ的振型频率值对比Table 4 Comparison of mode frequency values between model Iand model II

由表4可知，2种体系低阶振型阶次一致，第1阶振型为主梁1阶正对称侧弯，且基频相同。主梁侧弯频率没有变化，表明外伸跨有无吊索不影响主梁横向刚度；3跨连续体系竖弯频率总体低于单跨带外伸跨体系，其中1阶正对称竖弯频率降低了1.4%，表明外伸跨设置吊索使主梁竖向刚度略有减小；对于扭转振型，1阶扭转频率几乎无变化，表明外伸跨有无吊索对主梁扭转振动影响不大。由此可见，外伸跨有无设置吊索主要影响主梁的竖弯振型，设置悬吊外伸跨稍微降低了单跨悬吊悬索桥主梁的竖向刚度。因此对该加劲梁带外伸跨的悬索桥来说，单跨悬吊体系优于3跨悬吊体系。

4.3 不同加劲梁外伸跨布置形式对刚度的影响

现同时比较3种不同加劲梁外伸跨布置形式对结构动力特性影响，3种加劲梁外伸跨布置形式振型频率值如表5所示，图5为不同加劲梁外伸跨布置形式的频率对比。

由图5可知，传统单跨两铰体系自振频率曲线与另外2种体系有明显区别，主要是侧弯频率不同，因为传统单跨两铰体系的横向刚度相对更大。而传统单跨两铰和3跨连续2种体系前10阶频率曲线类似，表明悬吊跨数变化对自振特性总体变化影响不大。由表5可知，3种体系主梁竖弯和侧弯振型阶次一致，第1阶振型都为主梁1阶正对称侧弯，说明3种体系横向刚度都相对较小。传统单跨两铰体系主梁侧弯频率相对更大，以1阶正对称侧弯振型为例，另外2种带外伸跨体系(模型Ⅰ和模型Ⅲ)1阶正对称侧弯频率与其相比均降低了6.2%，表明设外伸跨后主梁的横向刚度略有减小；对于竖弯振型，由表5及图5可知，单跨带外伸跨体系主梁竖弯频率总体略微高于传统单跨两铰和3跨连续体系，以1阶正对称竖弯为例，分别提高了2.1%和1.4%，表明单跨带外伸跨体系主梁有更大的竖向刚度；对于扭转振动，由表5可知，3种体系1阶正对称扭转频率接近，即加劲梁外伸跨布置形式差异对扭转振动影响较小。而1阶扭转频率与1阶竖弯频率的比值，模型Ⅰ为2.12，模型Ⅱ为2.16，模型Ⅲ为2.13，说明不同加劲梁外伸跨布置形式对扭弯比影响不大。

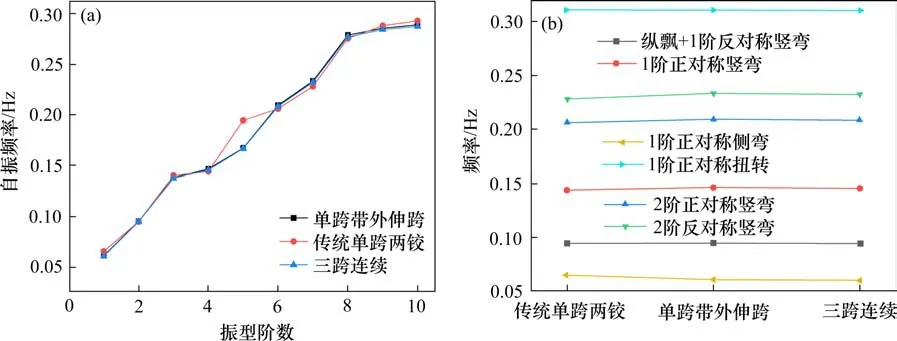
图5 不同加劲梁外伸跨布置形式的频率对比Fig.5 Frequency comparison of different stiffening girders’extended span layouts

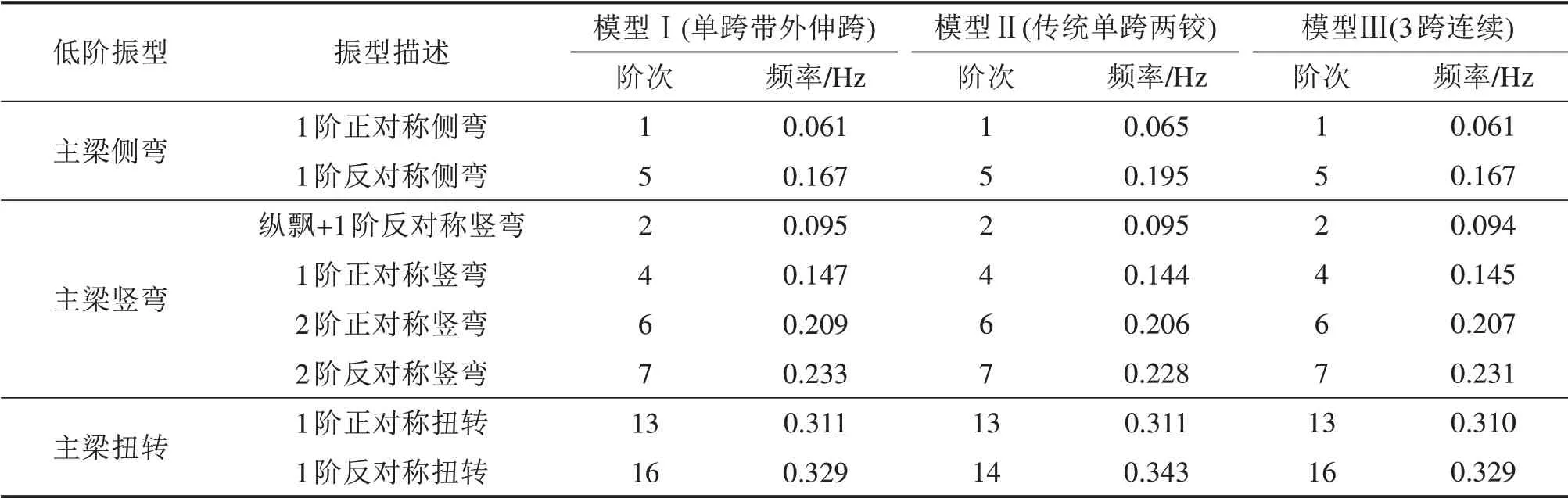
表5 不同加劲梁外伸跨布置形式的振型频率值Table 5 Vibration frequency values of different stiffening girders’extended span layouts

分析不同加劲梁外伸跨布置形式的动力特性可知：单跨带外伸跨体系在这3种体系中主梁有更大的竖向刚度；传统单跨两铰体系设置外伸跨可以一定程度上提升主梁竖向刚度，而主梁横向刚度略有减小；而外伸跨设置吊索则稍微降低了主梁的竖向刚度；不同外伸跨布置形式对扭转振动及扭弯比影响较小。由此可见，该单跨带外伸跨体系优于传统的单跨两铰体系和3跨连续体系。

5 加劲梁约束体系分析

5.1 增设塔-梁横向约束

模型Ⅰ(单跨带外伸跨体系)为全漂浮体系，相比传统单跨两铰结构体系，设外伸跨增大了纵桥向长度，会导致主梁横向刚度略有减小。为改进带外伸跨体系由于纵桥向长度增加而引起主梁横向刚度减小的问题，现进一步研究不同加劲梁约束体系对结构动力特性的影响。在该单跨带外伸跨悬索桥的桥塔处约束主梁的横向自由度，记为模型Ⅳ，建立该体系的有限元模型并进行模态分析，并与原模型Ⅰ进行比较。图6为模型Ⅳ的约束体系布置，表6为模型Ⅰ和模型Ⅲ的振型频率值对比。

图6 模型Ⅳ的约束体系布置Fig.6 Constraint system layout of model IV

由表6可知，对该单跨带外伸跨体系(模型Ⅰ)增设塔-梁横向约束，结构基频显著增大了55.7%，且第1阶振型变为1阶反对称竖弯伴随纵飘振型。模型Ⅳ竖弯和扭转频率几乎无变化，说明横向约束不影响主梁竖向刚度和扭转刚度。由侧弯振型可知，模型Ⅳ主梁侧弯振型阶次明显滞后，侧弯频率显著提高，其中1阶正、反对称侧弯频率分别增大了59.0%和41.3%，表明塔-梁横向约束对主梁横向刚度增大效果显著。由此可见，增设塔-梁横向约束可以显著增大单跨带外伸跨体系主梁的横向刚度。

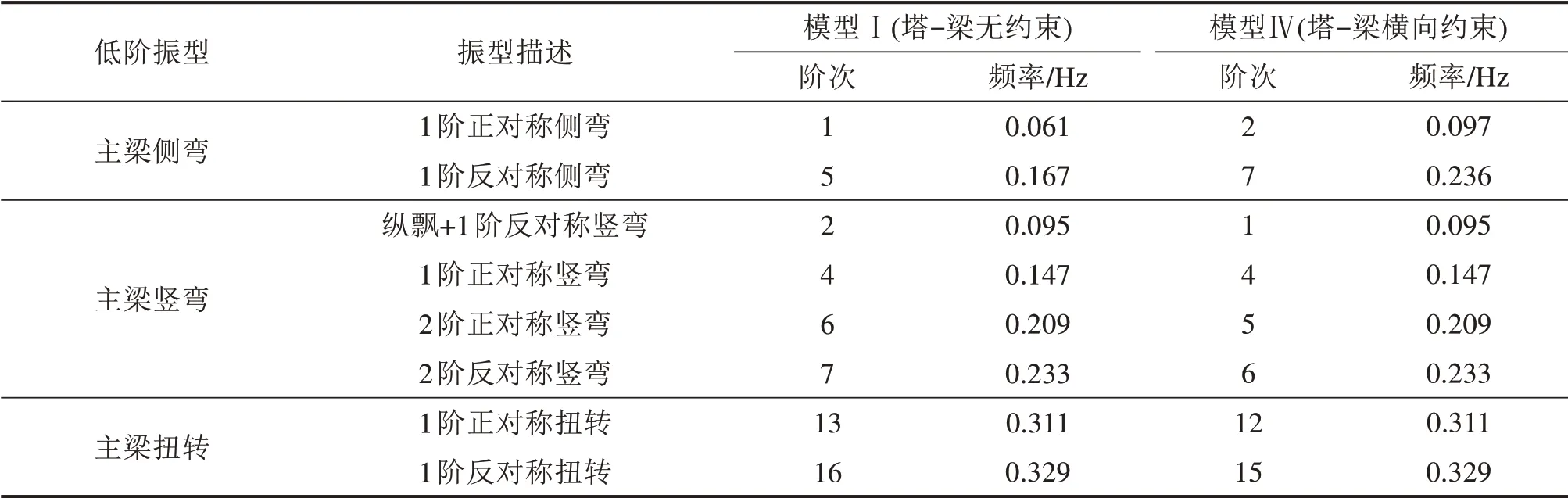
表6 模型Ⅰ和模型Ⅲ的振型频率值对比Table 6 Comparison of mode frequency values between model Iand model III

5.2 不同加劲梁体系对主梁横向刚度的影响

由前文可知，单跨带外伸跨体系(模型Ⅰ)相比传统单跨两铰体系(模型Ⅱ)，主梁横向刚度略有减小；而增设单跨带外伸跨体系塔-梁横向约束(模型Ⅳ)，显著增大了主梁横向刚度。因此进一步分析这3种加劲梁体系对主梁横向刚度影响，比较这3种模型主梁侧向振型，表7为3种模型主梁侧向振型对比。

表7 3种模型主梁侧向振型对比Table 7 Separate comparison of the girders’lateral vibration modes of the three models

由表7可知，模型Ⅳ主梁侧弯频率不仅显著大于模型Ⅰ，且相比模型Ⅱ也显著增大，以1阶正对称侧弯为例，增幅分别达59.0%和49.2%。由此可见，加劲梁约束体系对带外伸跨悬索桥刚度影响较大。对于该单跨带外伸跨体系，增设塔−梁横向约束不仅使其主梁横向刚度增大效果显著，且横向刚度显著大于传统单跨两铰体系。因此为提高带外伸跨悬索桥主梁的横向刚度，可以考虑在桥塔处增设塔−梁横向约束。

6 结论

1)该单跨带外伸跨悬索桥的基本周期符合同类大跨悬索桥柔性结构一般规律；该悬索桥的扭弯比为2.1；基频为横向振型，且竖向振型从第2阶出现，侧弯和竖弯出现较早，扭转出现较晚。

2)大跨度单跨悬索桥通过设置外伸跨可以在一定程度上提升主梁的竖向刚度，而主梁的横向刚度有所减小；若在悬索桥的外伸跨设置吊索会稍微降低主梁的竖向刚度，而对主梁的横向刚度没有影响。

3)单跨带外伸跨体系主梁的竖向刚度相对更大，该单跨带外伸跨体系优于传统单跨两铰体系和3跨连续体系；不同加劲梁外伸跨布置形式对扭转刚度和扭弯比影响较小。

4)若对该带外伸跨单跨悬索桥增设塔−梁横向约束，可以显著增大该悬索桥主梁的横向刚度，且主梁的横向刚度也显著大于传统单跨两铰悬索桥，以1阶正对称侧弯为例，增幅分别达59.0%和49.2%。

对该悬索桥方案，建议采用增设塔−梁横向约束的加劲梁带外伸跨单跨悬吊体系。在今后的大跨度悬索桥设计中，可以尝试通过改变加劲梁约束体系以达到改善结构刚度的目的。本文只对提出的加劲梁带外伸跨的单跨悬吊悬索桥方案进行初步动力性能分析，未分析结构的静力性能，特别是梁端转角和梁端位移，因此体系的合理性有待进一步研究。