大跨度山区桥梁风特性数值模拟及试验研究
2022-05-17周继王新国刘志文陈祥艳
周继,王新国,刘志文,陈祥艳
(1.中铁第四勘察设计院集团有限公司,湖北 武汉 430063;2.湖南大学 土木工程学院,湖南 长沙 410082)
山区铁路常需修建高陡峡谷桥梁,此时山区峡谷桥梁桥位风特性,如设计风速、风攻角和湍流度[1]等在山区桥梁抗风设计中起到了非常重要的作用。由于山区峡谷与平原地区的风场特征完全不同,对山区峡谷桥位处风参数的合理取值或模拟至关重要[2]。我国现行的桥梁抗风设计规范[3]通常是根据地表类别和地形条件,对平坦地形进行数值系数修正来确定风的大小,不能真实反映实际桥位处的风速大小。理论研究、现场实测[4]、数值模拟和试验研究是研究风环境的主要手段。理论研究仅用于预测坡度足够低的简单地形上的加速效应,不能用于复杂地形风特性。现场实测虽然被认为是研究风特性最可靠的方法,但通常昂贵且耗时,并且只能提供有限测点的风场数据。过去30年来,KOZMAR等[5]对复杂山区地形的风特性进行了试验研究。BOWEN[6]指出,复杂地形模型的几何尺度不应小于1/2 500~1/5 000。然而,工程实践中不存在通用风特性模型来描述山区风环境,因此对复杂山区峡谷地形风特性进行数值模拟对山区大跨桥梁抗风设计显得尤为重要和迫切。受制于模型试验条件和硬件条件,风洞试验与数值模拟的模型必然为有限范围的区域,此时地形模型边缘形成“人为峭壁”。“人为峭壁”的存在使入口边界的实际风特性与理论风特性发生偏离。针对“人为峭壁”对风洞试验的不利影响,一些学者提出了不同的解决方案。MAURIZI等[7-8]使用倾斜边界过渡段连接地面和地形模型顶部。胡朋等[9]提出了一种适用于复杂地形的曲线过渡段,认为这种过渡段比传统的倾斜过渡段具有更好的气流过渡性能。刘志文等[10]提出了一种改进的边界过渡段,通过结合Witozinsky曲线和直线来修改入口边界。随着计算流体力学(CFD)的发展,UCHIDA等[11−12]用CFD方法研究了复杂地形上的风特性。虽然目前国内已进行过复杂地形的CFD模拟研究,但不同的边界过渡段对不同复杂程度地形的数值模拟结果影响较大,边界过渡段的合理选择仍是山区地形模型研究的重要内容。本文以在建的贵州瓮马铁路北延伸线工程湘江特大桥为例,研究山区峡谷桥位风特性及地形模型边界过渡段的效果。以大桥中跨为几何原点,对直径8 km的区域进行风场特性CFD数值模拟;同时制作了比例尺为1:1 500的地形模型,对有无边界过渡段的情况分别进行了风洞试验,得到了典型监测位置处的纵向风剖面、桥面风速、风攻角等风特性参数,对分析湘江特大桥峡谷风效应、支撑大桥抗风设计具有重要的指导意义。
1 工程概况
瓮马铁路北延伸线工程湘江特大桥位于贵州省瓮安县境内,北侧临近遵义市,桥位轴线沿西北−东南走向,大桥轴线与东西连线夹角为28.7°。大桥为(120+235+235+120)m三塔预应力混凝土部分斜拉桥,最大墩高164.5 m,为目前在建世界铁路桥梁最高墩,如图1所示。

图1 湘江特大桥立面图Fig.1 Elevation of Xiangjiang River Bridge
桥位两岸地形整体西南东北较高,西北东南较低,峡谷地段为一个边坡较陡的V形地带,地形条件复杂,山峦起伏,两岸岸坡陡峭。图2中绿线所示即为湘江特大桥在地形上的水平投影。
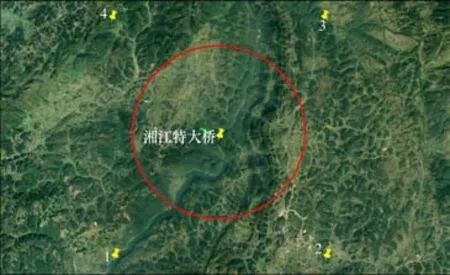
图2 湘江特大桥桥位处地形图Fig.2 Topographic map of Xiangjiang grand bridge
考虑到大桥桥面较高且处于海拔较高的峡谷地带,风对桥梁的作用不容忽视,利用规范和理论研究无法得到可靠的风特性参数,因此必须依靠数值分析和风洞试验来模拟桥位处真实风环境。
2 桥位地形CFD数值模拟
2.1 桥位地形曲面拟合及网格划分
通过Google Earth获得精度为20 m的地形高程数据,采用逆向工程软件Imageware拟合高程数据得到桥位地形曲面[13]。继而将拟合后的曲面导入网格划分软件ANSYSICEM生成计算域网格。计算域整体布置为8 km(直径)×2 km(顶面高程),桥梁轴线中心为计算域中心,计算域及边界条件见图3(a)。
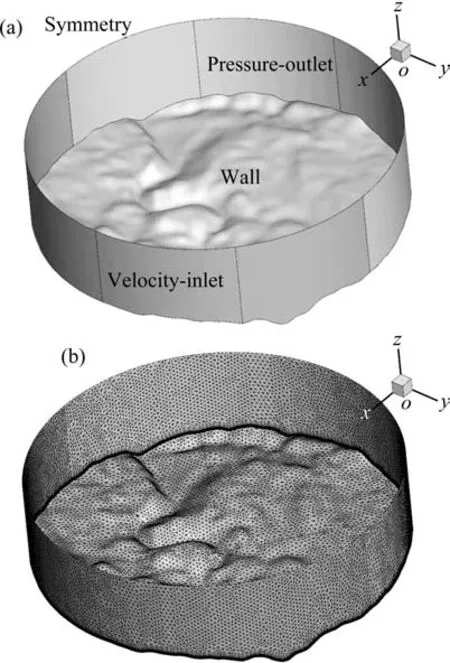
图3 计算域边界条件及网格细节Fig.3 Boundary conditions and mesh details of the computational domain
网格划分细节见图3(b),为局部加密桥梁所在高度与地面间的区域,采用首层网格高度为1.0 m[14],网格增长率为1.2进行边界层网格划分。为适应剧烈起伏的山区地形,地面采用适应性较好的三角形网格。指定最大网格尺寸100 m,网格总数约为165万。
2.2 边界条件设置
取入口处边界地表类型为B类地表,入口边最低点高程为风剖面计算起点,B类地表对应的梯度风高度为350 m,梯度风高度以上部分风速取为定值V∞=44.2 m/s,该值根据湘江特大桥虚拟气象站对应的开阔区域B类场地10 m高、10 min平均时距风速为V10=25 m/s计算得到。入口风速计算公式如下:
高程H≥h0+350 m时,
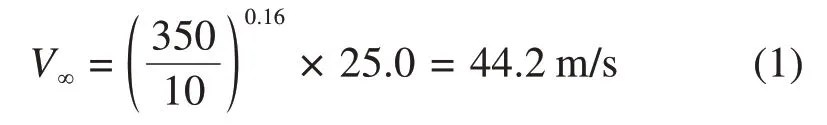
高程H≤h0时,

高程h0≤H≤h0+350 m时,
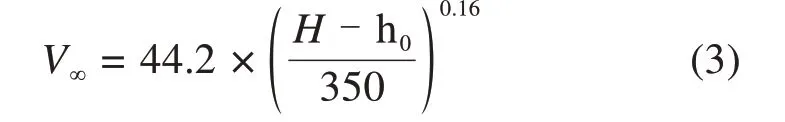
式中:H为风速点高程,m;h0为入口边界最低点高程,m;V∞为来流风速,m/s。
入口侧的半圆边界为速度入口(Velocity-inlet),另外半侧为压力出口(Pressure-outlet),计算域顶部为对称边界,计算域底部为壁面边界(Wall),粗糙度为0.03 m。
2.3 边界条件设置
计算共设8个工况,如图4(a),通过改变速度入口边界位置来实现不同来流风偏角的切换[15]。
1)计算得到不同工况下顺风向风速、横风向风速、竖向风速分量分别用Vx,Vy和Vz表示,风速分量的正负与ANSYSFluent保持一致,即西风时Vx为正,Vy=0,北风时Vx=0,Vy=0为正,Vz竖直向上为正;
2)风攻角(竖直面)定义为合风速与水平合速度的夹角,见图4(b):
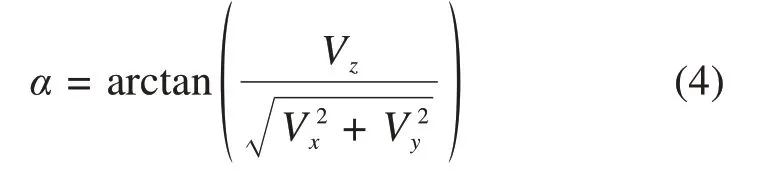
3)风偏角(水平面)定义为水平面合风速与桥轴线法线夹角,当水平面内风速沿桥轴线法向分量由西南指向东北时,横桥向风速为正,反之为负,图4(b)所示横桥向风速即为正;顺桥向风速由西北指向东南为正向,反之为负,图4(b)所示顺桥向风速为正:
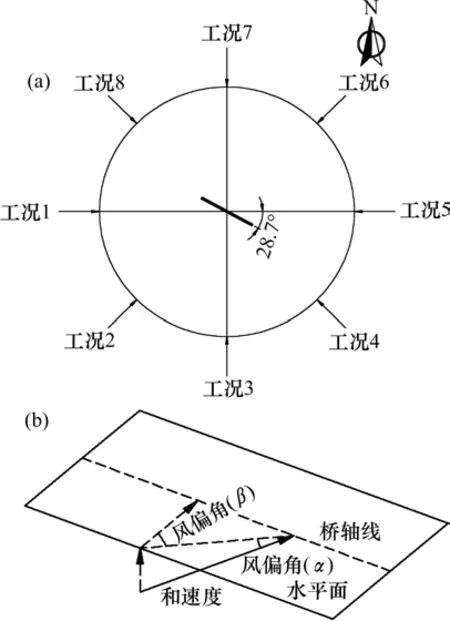
图4 桥位风场计算工况及风速方向定义示意图Fig.4 Schematic diagram of bridge site wind field calculation condition and wind speed direction definition
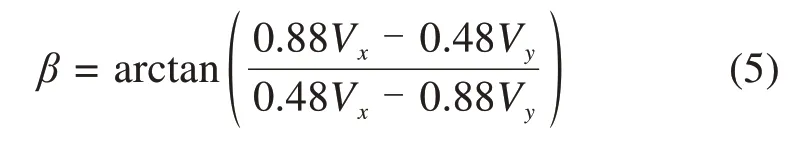
2.4 风速监测点设置
2.4.1 桥轴线方向监测点
沿大桥桥轴线方向设置20个监测点,见图5。1号监测点位于大桥遵义端,20号监测点位于瓮安端,监测点在桥面上均匀分布。进行流场模拟时同步监测横桥向、顺桥向和竖向的速度分量时程。
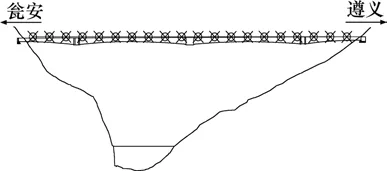
图5 桥位处沿桥轴线方向监测点位置设置示意图Fig.5 Schematic diagram of monitoring point location along bridge axis at bridge location
2.4.2 风剖面监测点
分别在大桥瓮安侧1/4位置、跨中位置处、遵义侧1/4位置处设置沿高度方向的监测断面[16],分别设置30,39和20个监测点,相邻监测点竖向间距为5 m,由近地面处延伸至桥面以上30 m处,如图6所示。
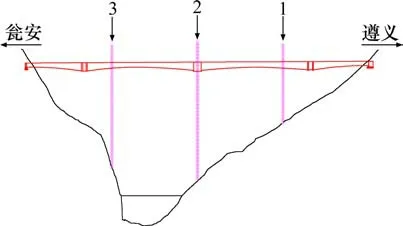
图6 桥位处各竖向风剖面监测断面及监测点位置布置Fig.6 Layout of monitoring sections and monitoring points of each vertical wind profile at bridge site
2.5 数值模拟结果分析
以工况1(正西风,风偏角为β=61.3°)为例,图7为桥面高度处各监测点横桥向、顺桥向和竖向风速沿桥轴线方向变化曲线(横坐标起点为遵义侧,终点为瓮安侧)。由图7可得,工况1时,桥面高度处风速总体靠近遵义侧较小,靠近瓮安侧较大;主梁高度处横风向平均风速为Vmean=20.0 m/s,约为来流处横桥向基本风速V10cos61.3°=12.0 m/s的1.67倍;主梁高度处顺风向平均风速为Vmean=28.8 m/s,约为来流处顺桥向基本风速V10sin61.3°=21.9 m/s的1.32倍。图8所示为桥面高度处各监测点风攻角沿桥轴线方向变化曲线。由图8可知,靠近峡谷两侧处风攻角变化较大,风攻角范围为α=−21.2°~4.3°。
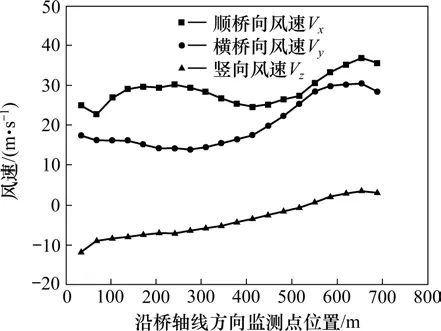
图7 工况1:风偏角为β=61.3°时监测点风速沿桥轴线分布Fig.7 When the wind deflection angle is 61.3 degrees,the wind speed at the monitoring point is distributed along the bridge axis
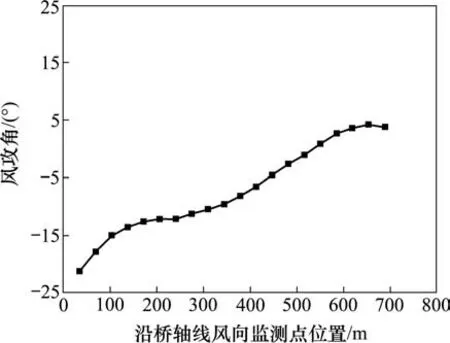
图8 工况1:桥面高度处沿纵桥向监测点位置风攻角分布Fig.8 Case 1:Distribution of wind attack angle at monitoring points along longitudinal direction at bridge deck height
图9所示为跨中位置处各监测点横桥向、顺桥向和竖向风速对应的风剖面图。横桥向风速风剖面在距离地面5~60 m范围内随高度的增加风速减小,在60~150 m范围内随高度的增加而逐渐增大;顺桥向风速随高度增加先减小到0后逐渐增大;竖向风速在距离地面5~100 m高度范围内略有变化,在100~150 m高度范围内随着高度的增加趋近于稳定值。
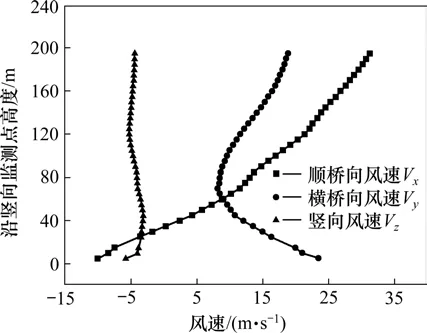
图9 工况1:跨中位置处监测断面风剖面分布Fig.9 Case 1:Wind profile distribution of monitoring section at midspan position
由桥位地形CFD的计算结果,可建立各工况下桥面高度处横桥向、顺桥向风速与入口边界处基本风速V10对应的横桥向、顺桥向风速之间的比值汇总,见表1。由表1可知,风偏角为β=16.3°,β=-163.7°时(即沿横桥向吹风时),桥面高度处横桥向风速平均值分别为20.7 m/s和27.3 m/s。桥面高度处横桥向风速、顺桥向风速与来流基本风速对应的横桥向风速、顺桥向风速对应的比值平均值分别为1.28和0.83。
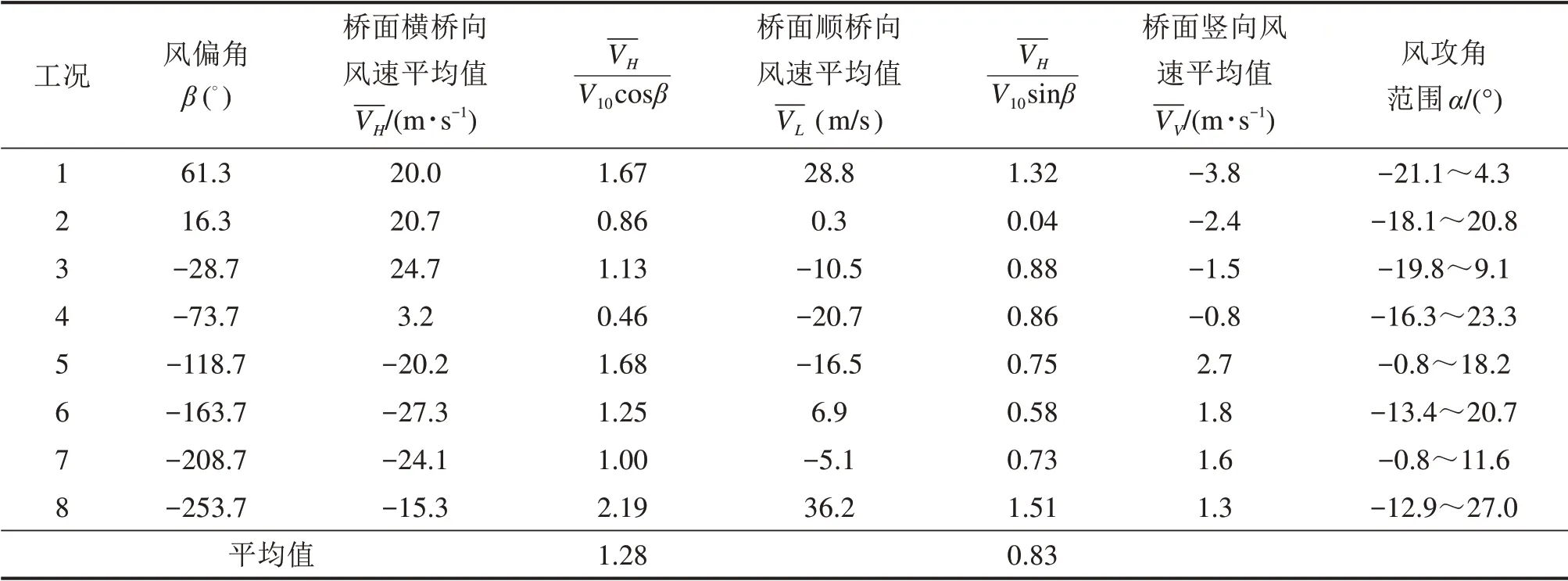
表1 各工况桥面风速与入口边界基本风比值、风攻角结果Table 1 Results of the ratio of the wind speed of the bridge deck to the basic wind at the entrance boundary and the wind attack angle under various conditions
由此,湘江特大桥桥面高度处设计基准风速为Vd=32.0 m/s,即为来流处桥位基本风速V10=25 m/s的1.28倍。此外,根据《公路桥梁抗风设计规范》(JTG/T 3360-01-2018)确定的主梁设计基准风速为Vd=30.3 m/s,较本文采用CFD方法确定的主梁设计基准风速偏小约1.70 m/s。
3 桥位地形模型风洞试验
3.1 地形模型设计与制作
为解决模型边界的“人为峭壁”问题,选取维多辛斯基曲线作为过渡段基本曲线形式[9]。采用CFD计算流体动力学方法对不同曲线参数进行计算,并结合关联度权重确定法确定最优过渡段曲线参数。风洞模型试验采用几何缩尺比[1]为1:1 500地形模型进行研究。选择以桥址中心为圆心,半径R=4 km范围内地形进行模拟,对应的地形模型直径为D=5.33 m。地形模型采用分块化制作,材料选用硬泡沫,如图10。

图10 湘江特大桥桥位有无过渡段地形模型对比Fig.10 Comparison of terrain models of Xiangjiang River Bridge with or without transition section
3.2 试验工况
试验研究有、无过渡段对桥位桥面高度处横桥向风速、风剖面、风攻角以及桥梁总长1/4跨、1/2跨、3/4跨风剖面的影响。此外,西、南、东、北4个方向分别定义为工况1,2,3和4。如工况1为正西风来流,风向逆时针旋转为正,具体风工况见图11。
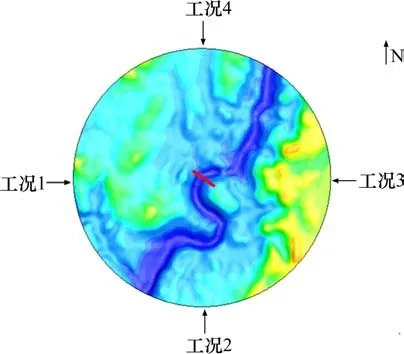
图11 风工况示意图Fig.11 Schematic diagram of test conditions
3.3 试验结果分析
3.3.1 测试断面处风剖面
以正南风即工况2为例,图12为工况2下各测试断面处的平均风速剖面图,图12中横坐标为顺风向归一化风速,竖坐标为监测点距地表高度。其中顺风向归一化风速=监测点处风速/来流方向参考点风速。取距地面12 m风速为参考风速,对图12中风剖面指数进行拟合计算,见表2。由表2可知,局部地形对风剖面指数影响较大,对1号剖面,风剖面指数小于入流,风速沿竖向变化较小;2号和3号剖面风剖面指数均大于入流风速剖面指数,即地形对风速的阻挡效应明显,近地面风速较小。总体而言,有过渡段时风剖面指数大于无过渡段风剖面指数,即地形的阻挡效应更加明显。
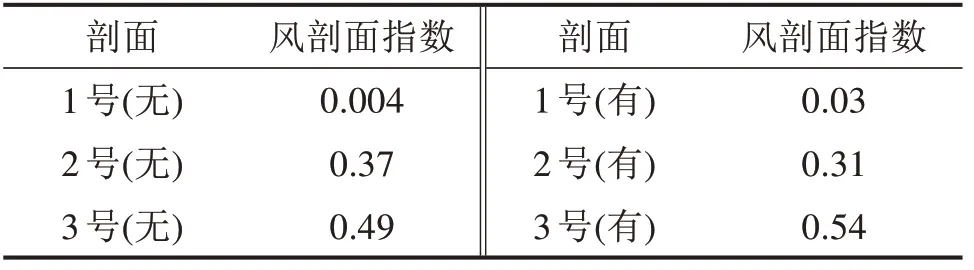
表2 工况2不同测试断面风剖面指数拟合结果Table 2 Wind profile exponent fitting results of different testsections in case 2
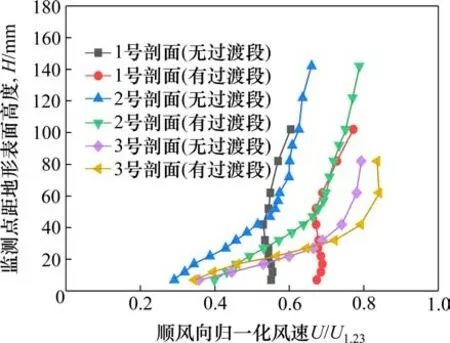
图12 工况2不同测试断面平均风速剖面图Fig.12 Average wind speed profile of different test sections in case 2
由试验结果分析,南风时,设置过渡段的地形模型的顺风向归一化风速均大于无过渡段的地形模型。发生此种现象的原因在于:来流风受地形模型峭壁的阻挡,形成气流剪切层,剪切层发展范围扩大,导致风抵达桥位处时,风速有一定程度降低。而当地形模型设置过渡段时,“人为峭壁”现象被削弱,剪切层现象不明显,风速干扰相对较小。
3.3.2 主梁高度处横桥向风速
以正西风即工况1为例,图13为工况1下主梁高度处各监测点位置横桥向风速比,从试验结果来看,无论地形模型设置过渡段与否,横桥向风速比在纵桥向均呈现先增大后减小的趋势,且有过渡段的风速比值大于无过渡段时的情况;桥跨中央处横桥向风速总体较大,与来流边界层高度处风速之比最大值约为0.764(考虑过渡段)。根据不同工况试验结果,当地形模型设置过渡段时,70%以上监测点处的主梁高度处横桥向风速要大于无过渡段的地形模型情况,发生此种现象的原因与风剖面试验结果呈现差异化的原因一致。
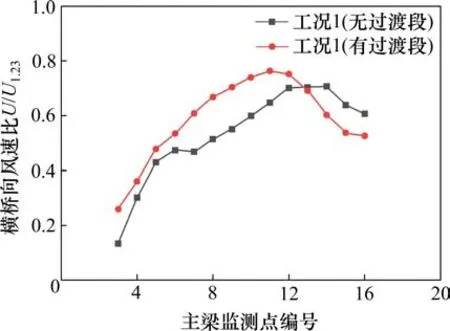
图13 工况1主梁高度处不同测点位置横桥向风速比Fig.13 Transverse bridge wind speed ratio at different measuring points at girder height in case 1
不同试验工况下,主梁高度处横桥向风速与来流入口处基本风速比值汇总如表3所示。由表3可知,不同工况下主梁高度处横桥向风速与来流入口梯度风速比值均值分别为0.534 1(无过渡段)和0.626 7(有过渡段)。不同工况下主梁高度处横桥向风速与来流入口基本风速比值均值分别为0.944 2(无过渡段)和1.108 0(有过渡段),比地形模型CFD数值模拟结果1.28偏小。
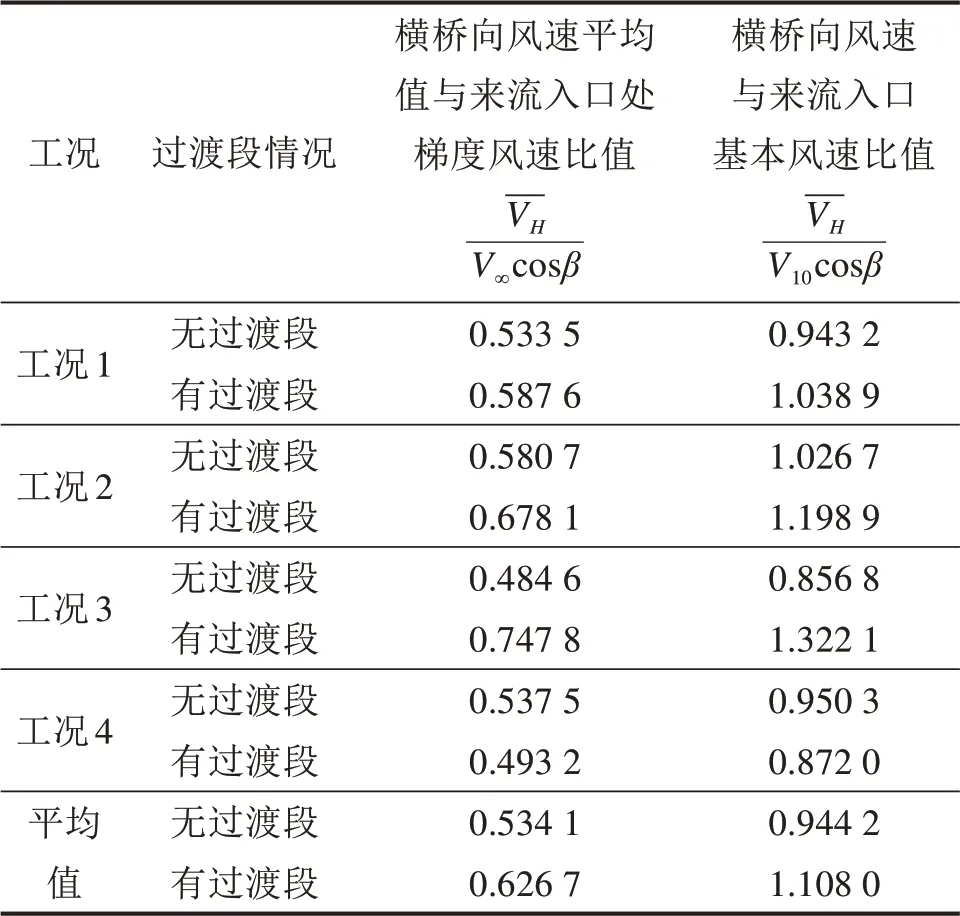
表3 主梁高度处横桥向风速与来流入口处基本风速比值Table 3 Ratio of transverse wind speed at girder height to basic wind speed at inlet
3.3.3 主梁高度处风攻角
以正北风即工况4为例,图14为布设于主梁上的监测点风攻角试验值。受桥址处V形峡谷地势以及周边山脉地形的影响,主梁两端的风攻角差异较大,主梁中部范围差异较小。将主梁中部范围定义为II区,主梁两端范围定义为I区、Ⅲ区,不同工况下不同分区攻角变化范围见表4。风攻角沿桥轴线变化较为明显,当地形模型设置过渡段时,大部分监测点处的风攻角试验值要略小于无过渡段的情况,发生此种现象的原因在于过渡段的存在使得来流风经过地形模型时,气流变化平缓,风的湍流度较为平和。

图14 有无过渡段工况4主梁高度处风攻角Fig.14 Wind attack angle at the height of main girder with or without transition section in case 4
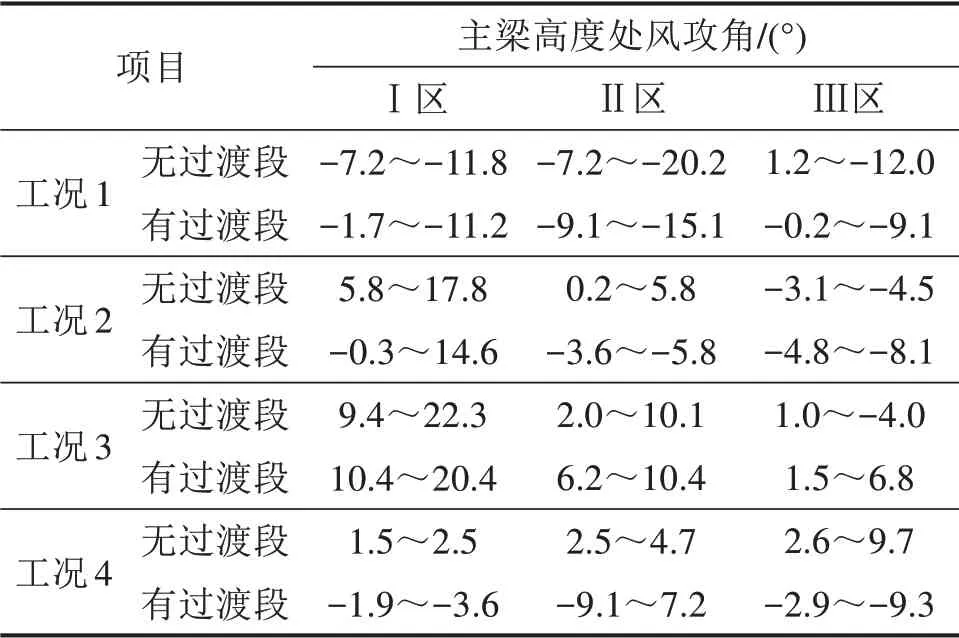
表4 不同分区主梁高度处风攻角变化范围Table 4 Variation range of wind attack angle at girder height in different zones
工况2与工况3主梁两端风攻角差异较大原因在于主梁位于S形峡谷之间山腰处,此处主梁风攻角受峡谷两侧山体的遮挡作用及越山风尾流影响。由表4可知,考虑过渡段影响,南风(工况2)和北风(工况4)时,峡谷中央区域主梁高度处风攻角范围分别为−5.8°~−3.6°和−9.1°~7.2°。
4 结论
1)桥位地形模型试验结果表明,不同工况下主梁高度处横桥向风速与来流入口基本风速比值均值分别为0.944 2(无过渡段)和1.108 0(有过渡段),比地形模型CFD数值模拟结果1.28偏小。综合考虑,湘江特大桥桥面高度处设计基准风速可按Vd=1.28V10=32.0 m/s进行工程设计。
2)采用最优过渡段使风速剖面逐渐抬升,气流过渡平缓,来流风速降低程度较无过渡段时小且风速受到的干扰较小。无过渡段的地形模型,风易受地形模型峭壁的阻挡,形成气流剪切层,“人为峭壁”会降低主梁高度处的横桥向风速。
3)桥位地形模型风洞试验结果表明,考虑过渡段影响,当南风(工况2)和北风(工况4)时,峡谷中央区域主梁高度处风攻角范围分别为−5.8°~−3.6°和−9.1°~7.2°。
4)本文采用数值模拟和风洞试验来模拟桥位处风环境,得到了大跨度山区桥梁风特性的一些重要参数和变化规律,对同类型桥梁的抗风设计具有很好的指导和参考作用。
