弱电网下具有宽频特性的并网逆变器阻抗重塑研究

郑国超严柏平王富立黄大卓沈春城

(1.广东工业大学自动化学院,广东 广州 510006;2.广东电网有限责任公司潮州供电局,广东 潮州 521000)

0 引言

随着化石能源日渐消耗枯竭,光伏发电等分布式发电技术得到快速发展[1]。分布式发电系统之间具有散落状分布的特点,发电系统之间需要通过大量变压器及输电线路与大电网连接,因此,电网会引入不可忽略的电网阻抗,这种电网一般称之为弱电网[2]。在电网阻抗不可忽略的情况下,并网逆变器系统会出现电能质量变差[3]、谐波共振甚至系统不稳定等问题[4-5]。

目前,针对电网阻抗变化导致并网逆变器的稳定性变差问题,许多学者提出不同的解决方案。文献[6]采用基于D 分割法的逆变器PI参数设计的方法,通过满足相角裕度、幅值裕度、电流环带宽等性能指标快速准确选取弱电网下的PI参数,从而使系统稳定高效运行。但该过程设计复杂,计算量大。文献[7]通过加入基于电网阻抗测量技术的自适应环节实时调整开环增益,来适应电网阻抗的变化对系统稳定性造成的影响。文献[8]将准比例谐振控制器应用到光伏并网逆变器的电流控制中,使并网逆变器系统对弱电网有更强的适应性。文献[9]提出一种阻抗重塑方法,通过把电压前馈函数与二阶Butterworth 滤波器串联组合,对逆变器的中低频输出阻抗进行重塑,同时提高了系统对阻抗参数的鲁棒性。文献[10]提出一种包含电网阻抗检测、相位裕度补偿和幅值矫正单元的阻抗重塑方法,通过检测电网阻抗实时调整补偿环节参数,保证系统良好的稳定裕度,但该方法采用自适应控制,算法较为复杂,不易于实现。

经过上述对阻抗重塑方法的分析,研究一种对电网阻抗变化有较强适应性,且不采用自适应控制算法的阻抗重塑方法。本文通过建立LCL并网逆变器模型和分析输出阻抗和系统稳定裕度的关系,提出一种具有宽频率的重塑方法对逆变器等效输出阻抗进行重塑。所提重塑方法比传统重塑方法对弱电网有更强的适应性,并通过Matlab/Simulink仿真验证相关理论分析的正确性与重塑环节对系统稳定的作用。

1 LCL型并网逆变器阻抗模型建立

本文构建的三相LCL并网逆变器系统如图1所示,控制策略采用αβ坐标系下基于比例谐振调节器电流双闭环控制策略。与dq坐标系下建模相比,该控制策略基于静止坐标系并网电流外环控制,无需对电流分量进行解耦,其控制算法简单,而且采用αβ坐标系可以减小锁相环对系统的影响[11]。

图1 LCL并网逆变器系统结构

图中,L1、C和L2组成LCL 滤波器部分;Zg为电网阻抗分别为逆变器输出电流在αβ坐标系下的参考值;UPCC为电网公共耦合点处的电压;Ug为电网的电压;Udc为母线上的直流电压。Gi(s)为采用比例谐振控制的电流控制器;Gc(s)为阻抗重塑环节;Hi1与Hi2为电容电流反馈的比例系数和并网电流采样的比例系数;KPWM为三相逆变器的增益系数;Zg为电网阻抗。

根据逆变器系统控制结构图得到系统的等效控制框图,可把模型框图简化等效为图2所示,其详细等效过程可参考文献[12]。

图2 LCL并网逆变器等效控制结构

Gde(s)为控制延时传递函数,其表达式为

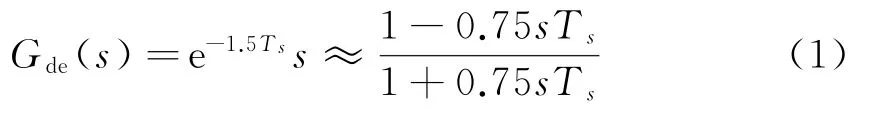
式中:Ts为系统采样时间。经过等效处理后,Ga(s)、Gb(s)的表达式分别为

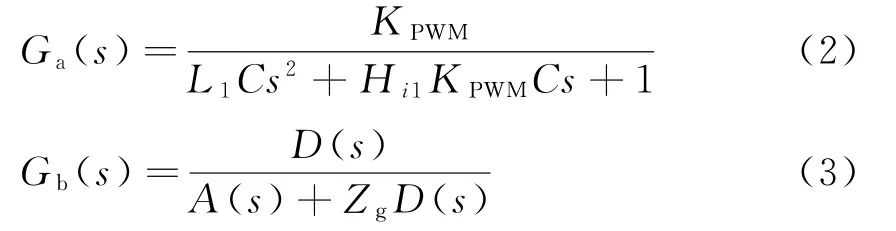
式中:Ga(s)、Gb(s)为系统简化等效的环节。

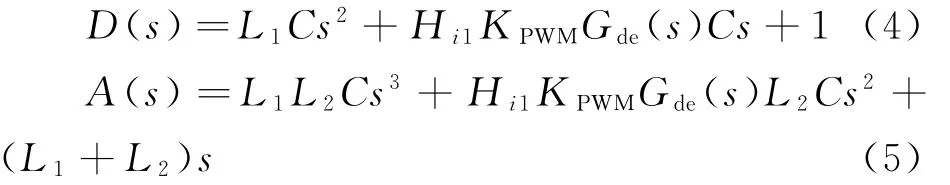
系统的环路增益TA(s)的表达式为

2 阻抗重塑模型及对象

考虑电网阻抗情况下,利用阻抗模型的频域分析方法对并网逆变器稳定性进行分析时,把系统分为并网逆变器的部分和电网部分来建模。并网逆变器在端口处等效为诺顿等效输出并联阻抗模型[13]。并网逆变器的等效模型与电网部分组成并网系统的等效电路,通过对该等效电路的推导与控制理论的分析,可得出传统基于阻抗的稳定性判据[12]。但是,该稳定性判据存在表征系统稳定裕度不准确等问题。高家元等人提出一种新的等效输出阻抗串并联模型能够很好解决这些问题[14]。新等效输出阻抗串并联模型所对应的并网系统的等效电路如图3所示。

图3 新的等效输出阻抗串并联模型等效电路

经过等效变换可得等效输出阻抗Zo1(s)和Zo2(s)的表达式为

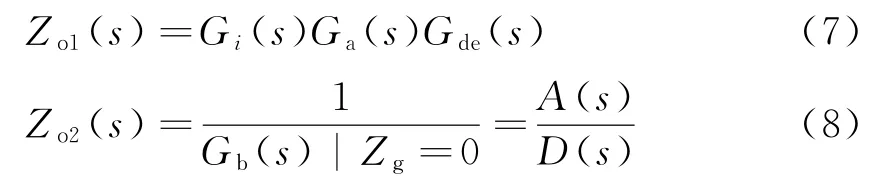
式中:Zo1(s)和Zo2(s)为等效输出阻抗分量。

由图3可知,该电路为线性电路,可由电路理论中的叠加定理得到并网电流表达式

根据文献[14]的研究结果可知,并网逆变器系统的真实相位裕度可由[Zo2(s)+Zg(s)]/Zo1(s)的相位来表征。所以系统的真实相位裕度PM 可由式(10)得出

式中:jωcross为Zo2(s)+Zg(s)与Zo1(s)在交截频率处的频率。

图4 给出不同电网阻抗条件下Zo2(s)+Zg(s)与Zo1(s)的伯德图。

图4 不同电网阻抗条件下Z o2(s)+Z g(s)与Z o1(s)的伯德图

由图4可知,当电网阻抗逐渐变大时,Zo2(s)+Zg(s)的幅频特性曲线就会向左上方移动,同时相频特性曲线更接近90°,Zo1(s)与Zo2(s)+Zg(s)在交截处的频率也不断减小。根据式(10)可知,系统的相位裕度不断减小,导致系统的调节时间变长和动态性能变差,甚至会导致系统振荡。所以,应对电网阻抗增加导致系统稳定裕度减小这种问题,需要在系统环路中增加具有相位补偿功能的重塑环节,以提高交截频率处的相位裕度,从而提高逆变器并网电流谐波抑制能力。通过式(2)和式(7)可知,Zo1(s)在并网逆变器的参数确定后将会保持不变,电网阻抗的变化不会对其产生影响,因此,可选择Zo1(s)作为重塑对象。

3 宽频阻抗重塑方法的设计与实现

为保证逆变器并网系统在电网阻抗变化时依然保持良好的稳定裕度,采用重塑环节Gc(s)对Zo1(s)进行阻抗重塑,重塑后的等效阻抗模型如图5所示。

图5 重塑后的等效阻抗模型

重塑后的等效阻抗Zo1N(s)表达式为

根据重塑后的等效阻抗模型,可得知系统的稳定性可用Zo2(s)+Zg(s)与[Zo1(s)Gc(s)]交截频率处的相位裕度进行表征,重塑后相位裕度N的表达式如下

由式(12)可知,Gc(s)要在交截频率处提供超前的相位,以提高系统在交截频率处的相位裕度。为了实现对交截频率处的定点相位补偿,Gc(s)不仅要具有相位补偿,还要有幅值矫正功能。Gc(s)引入的幅值增益可能会造成交截频率偏移,所以要求Gc(s)对Zo1(s)的幅值矫正,保证在交截频率处Zo1(s)的幅值保持不变,即约束条件为

电网阻抗的改变会导致交截频率产生偏移,从而使系统的稳定裕度降低。所以需要Gc(s)能够在交截频率附近的频段提供相位补偿,减弱电网阻抗变化对系统稳定性带来的影响。传统阻抗重塑方法[15]虽然也能实现对交截频率处的定点相位补偿,但是在应对更大电网阻抗时,系统的稳定裕度不足。为了能使并网逆变器系统对弱电网有更强的适应性,则需要提高等效输出阻抗在低交截频率频段的相位裕度,本文提出一种新型阻抗重塑的方法。该阻抗重塑方法表达式如下

式中:c、f为常数。根据式(14)可求得Gc(s)的补偿相位ϕ(ω)的表达式为

由式(15)可知,Gc(s)的补偿相位的角度由常数c、f控制。当补偿的角度为45°时,常数c控制的角度与常数f控制的角度可以组合为75°减去30°,可以求出c=7.5958,f=1.732。图6给出传统和新型阻抗重塑环节在补偿相位角度为45°时的伯德图。

图6 传统与新型阻抗重塑环节伯德图

由图6可知,阻抗重塑环节在低于交截频率频段的相位都为正,这能够为等效输出阻抗的低频段提供相位补偿。新型阻抗重塑环节能够在交截频率附近较宽的频段提供45°的补偿相位,而且在整个频段提供的相位都大于传统重塑环节提供的相位。采用2种不同的重塑环节Gc(s)对Zo1(s)进行阻抗重塑,重塑前后阻抗Zo1(s)的伯德图如图7所示。2种重塑环节重塑后的阻抗Zo1(s)在交截频率处的相位都得到提高,但在远离交截频率处新型重塑的阻抗Zo1(s)能获得较高的补偿相位。

图7 重塑前后等效输出阻抗伯德图

结合图4与式(12)可知,在电网阻抗变大时,经过新型阻抗重塑环节重塑后的系统能够获得更高的相位裕度。因此,新型阻抗重塑环节可以使并网逆变器系统对弱电网有更强的适应性。

4 仿真及结果分析

为了验证本文所提重塑方法的合理性与有效性,在Matlab/Simulink 软件上搭建一台额定功率为14 k W,电压为220 V,频率为50 Hz的三相LCL型并网逆变器进行仿真验证。系统的主要仿真参数如表1所示。

表1 LCL并网逆变器系统参数

为了更加直观地展示电网阻抗对并网电流的影响以及所提阻抗重塑环节的有效性。仿真实验中分别在Lg=0 m H,Lg=5 m H,Lg=9 m H 3种不同电网阻抗的环境中运行,并在0.5 s时投切阻抗重塑环节。根据基于阻抗的并网逆变器稳定性判据,在研究电网阻抗对并网逆变器系统稳定性的影响时,要保证系统在没有考虑电网阻抗时并网逆变器系统能保持稳定运行。LCL并网逆变器系统在Lg=0 m H 时的三相并网电流仿真波形如图8所示。

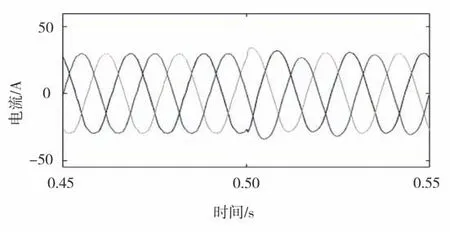
图8 L g=0 mH时的并网电流仿真波形

从图8可知,当Lg=0 m H 时,系统能稳定运行,并网电流的THD=2.5%,在阻抗重塑环节投切后很快能进入稳定状态,动态响应快。

增大电网阻抗会对并网电流的质量以及系统的稳定性产生影响,把电网阻抗增加到5 m H 时,三相并网电流仿真波形如图9所示。

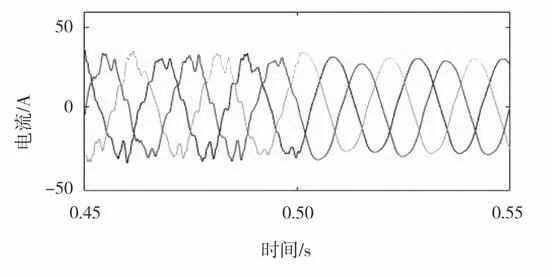
图9 L g=5 mH时的三相并网电流波形

由图9可知,当Lg=5 m H 时,系统仍然能稳定运行,但是并网电流的THD=11.86%,不符合并网的标准,在阻抗重塑环节投切后并网电流的质量有所改善,重塑后并网电流的THD=2.96%。阻抗重塑环节能有效抑制电网阻抗对并网电流质量的影响。

当电网阻抗为Lg=9 m H 时,系统就会变得不稳定。为了能证明所提阻抗重塑环节对弱电网有更强的适应性,在0.5 s时分别投切2种阻抗重塑环节,得到的单相并网电流仿真波形如图10所示。

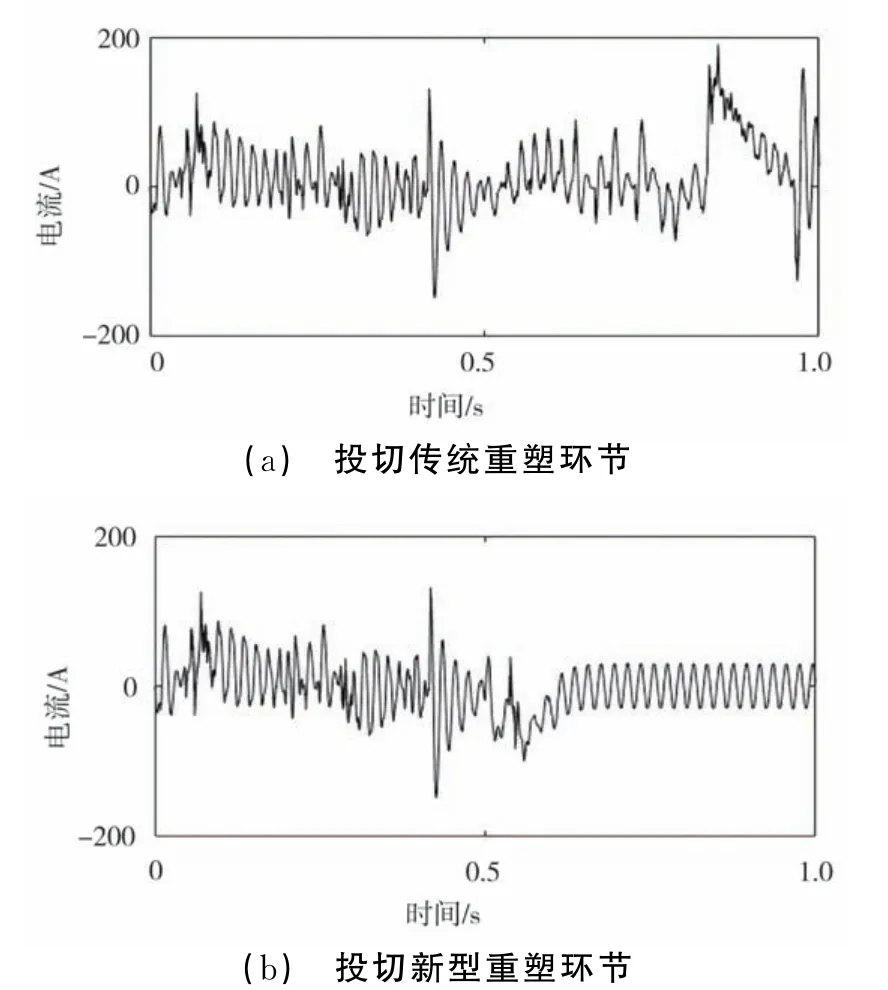
图10 投切传统和新型重塑环节时的并网电流波形

在投切传统阻抗重塑环节后,系统仍然处于不稳定的状态。而投切所提的新型阻抗重塑环节后,经过约为0.1 s的调整,系统进入了稳定的状态。

从理论分析以及仿真结果可知,所提的阻抗重塑方法能提高电网阻抗变化时系统的稳定裕度,该环节具有以下特点:

(1)该阻抗重塑环节能有效应对电网阻抗变化对逆变器系统稳定性的影响,而且能把并网电流的THD 控制在并网标准内。

(2)动态响应速度快,系统在投切阻抗重塑环节后系统能较快趋于稳定。

(3)系统设计和实现比较简单,在没有采用自适应控制的情况下,系统也能有效应对宽范围电网阻抗对系统稳定性的影响,而且也具有不错的控制性能。

5 结束语

电网阻抗的宽范围变化对并网逆变器系统的稳定性带来很大挑战。本文以三相LCL 并网逆变器为研究对象,针对系统输出等效阻抗对系统稳定性的影响,对并网逆变器系统输出等效阻抗进行重塑。提出一种具有宽频特性的稳定性补偿的阻抗重塑环节,该阻抗重塑环节可以宽频域提高等效输出阻抗的相位,使系统在应对更大的电网阻抗时仍然能保持稳定。该方法结构简单,在不使用自适应控制的前提下,能有效提高弱电网条件下系统的稳定性,而且易于实现,对工程中提高复杂电网条件下并网逆变器稳定性工程有一定的意义。在后续的研究中可以研究该阻抗重塑环节对于不平衡、电压暂降等条件下系统的稳定性。