小波包分解与SVM在电磁斥力机构故障诊断中的应用
2022-05-17龚森
龚 森
(广东电网广州供电局,广东 广州 510620)
目前,随着社会经济水平的不断提高,我国的电网规模也不断扩大,电力系统负荷也随之快速增长,导致很多地区的短路电流逐步逼近或已经超过电力系统现有的开断容量,对电力系统的安全构成严重威胁。故障限流器能够有效限制电网的故障短路电流,保证电力系统的稳定运行,而限流器的机械操动机构对限流器的性能有着非常重要的影响[1]。另外,由于我国能源分布十分不平衡,东部地区用电量越来越大,由此引出的输电问题也愈发凸显,而传统的交流输电相较直流输电存在输电稳定性、输电效率较低等问题,且存在同步问题,因此直流输电在我国得到了广泛的关注和研究。但直流输电系统对短路故障十分敏感,一旦没有及时切除故障电流,就会导致整个系统停运,因此需要一种快速开关来切断故障电流,保障直流输电系统稳定运行[2]。综上,在故障限流器和直流断路器等领域,对开关的分闸速度有非常高的要求,而基于电磁斥力机构的快速真空断路器开断速度在2~5 ms之间,满足上述领域的需求[3]。
然而,正是由于电磁斥力机构分闸速度很快,因此电磁斥力机构中的机械部件受到的冲击也很大,导致其相比弹簧操动机构更容易出现故障。而一旦电磁斥力机构出现故障,导致短路故障电流无法正常分断,就可能会造成十分严重的电力系统事故[4]。另外,根据国际大电网会议第三次调查统计结果[5],断路器操动机构机械故障和辅助回路电气故障是导致其故障的主要原因。因此,需要对故障限流器和直流断路器中的电磁斥力机构进行故障诊断,以预防电力系统事故的发生。
1 电磁斥力机构概述
电磁斥力机构的基本结构图如图1所示[6]。从图1可以看出,电磁斥力机构主要由操动机构和控制回路组成。其中,操动机构是主要部分,主要由连杆、分闸线圈、合闸保持永磁铁、衔铁、分闸保持永磁铁、斥力盘和合闸线圈组成;控制回路用于分合闸线圈的充放电控制,主要由充电电源、分合闸储能电容、分合闸控制晶闸管组成。其工作原理为(以合闸为例):充电电源预先向合闸电容充电,当接到合闸指令时,合闸控制晶闸管导通,合闸电容向合闸线圈放电,从而在合闸线圈中产生一个脉冲电流,由电磁感应定律可知,斥力盘中会感应出一反向涡流并与脉冲电流相互作用,从而推动斥力盘向上运动并带动连杆,完成合闸动作,分闸动作同理[7]。
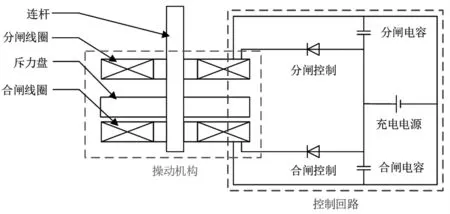
图1 线圈-盘式电磁斥力机构结构图
2 电磁斥力机构故障诊断
目前,断路器状态监测主要包括3个步骤:原始信号采集、信号特征量提取以及断路器故障诊断。原始信号主要包括高压断路器分合闸动作时产生的振动信号。振动信号是由断路器分合闸瞬间触头碰撞或与缓冲器撞击形成,并可引起整个操动机构的振动,因此,测量振动信号可以获得整个断路器机械结构的状态信息。另外,振动信号为非接触式测量,不会破坏断路器原有结构,且不会受到电磁干扰,目前在状态监测和故障诊断领域已有广泛的应用。
在获得断路器原始信号之后,就要对信号采用时频分析方法提取能够表征断路器状态的信号特征量,最后将特征量输入到故障诊断模型中,实现断路器的状态监测。特征提取方面,目前使用较多的是小波包分解,而支持向量机(SupportVector Machine,SVM)由于其在样本数较少的情况下,也可以达到较高的模型准确率,在故障诊断领域得到了广泛的应用。
2.1 小波包分解原理
小波包分解是一种线性时频分析方法,可以将信号的时间和频率信息同时表征出来,并且具有较好的时频分辨率,尤其对高频部分可以进行更为精细的分解。
小波包分解的递推计算公式为[8]:
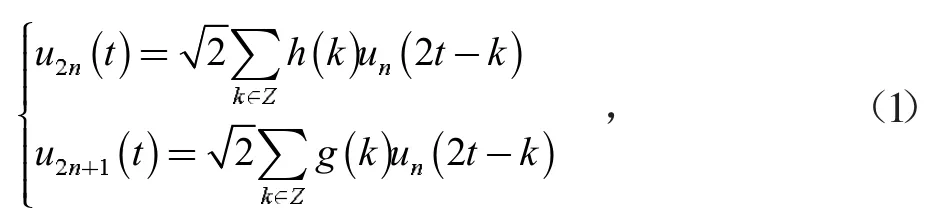
式中,u(t)表示输入信号;g(k)表示低通滤波器;h(k)表示高通滤波器;k为小波函数的位置坐标;n为小波函数的震荡次数。h(k)与g(k)满足:

即二者为正交关系。以三层小波包分解为例,原始振动信号S可以分解为:
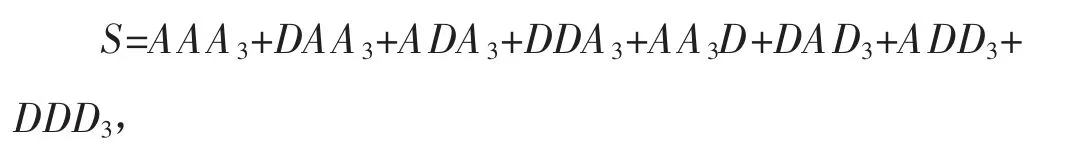
其中,A为低频分量,D为高频分量。三层小波包分解的示意图如图2所示。由图可知,三层小波包分解可以得到23即8个分解分量,有利于更加精细地提取信号的时频信息。
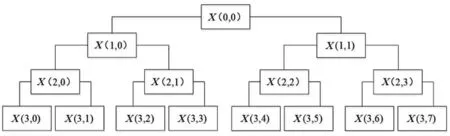
图2 三层小波包分解的示意图
电磁斥力机构的状态改变时,会引起振动信号能量分布的变化;另外,在能量理论中,熵是混乱程度的度量,与信号的不确定度有关[9]。因此,可以将小波包分解与能量熵相结合,作为表征电磁斥力机构状态的特征量。
假设电磁斥力机构的振动信号长度为L,小波包分解的层数为j层,对应的分解顺序为Xjk,(k=0,1,...,2j-1),则对应的小波包能量熵计算方法为:
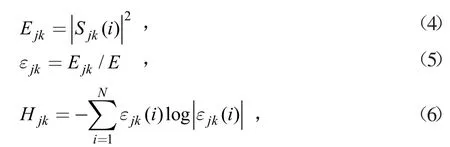
其中,Sjk表示第j层第k个分量,Ejk为Sjk的能量。E为所有分量的能量总和,εjk为Sjk的归一化能量,Hjk为Sjk的小波包能量熵。
2.2 SVM原理
SVM是一种基于统计学习理论的机器学习算法,而统计学习理论追求在小样本条件下,利用有限的信息得到最优的结果[10]。SVM的核心问题是寻找一个分类超平面,该超平面满足距离两侧样本距离最大。SVM的分类原理如图3所示。图3中,“○”和“■”分别代表2种不同类别的数据点,ωx+b=0代表分类超平面。ωx+b=-1和ωx+b=1分别代表2类数据点的支持向量超平面,Margin表示2类数据的分类距离。
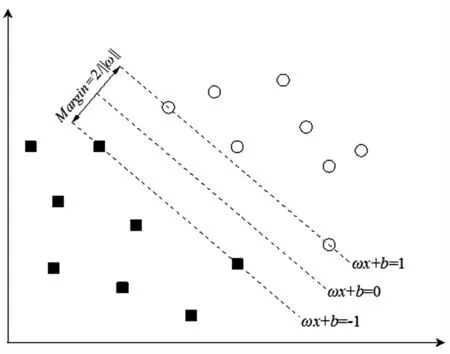
图3 SVM分类原理图

则SVM的原理可用以下最优问题表示:
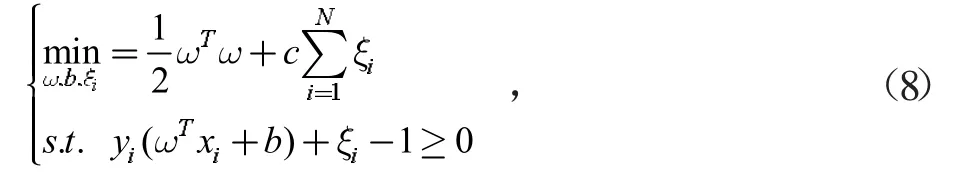
式中,ω和b分别为超平面坐标参数,ξi为松弛因子,c为惩罚因子,ξi≥0,1≤i≤N。
2.3 故障诊断结果
本文采用持续监测某样机中电磁斥力机构寿命试验的方法,监测过程中电磁斥力机构共分合闸250次,共采集247组分闸信号,采集有效信号210组,其中正常状态信号183组,故障状态信号27组,故障类型3种,分别为连杆弯曲、分闸不到位以及电容充电电压过高。
选取小波包分解层数为5层,则可以得到一个32维的小波包能量熵行向量,记为[W1,W2,…,W32]。4种不同状态信号的小波包能量熵对比如图4所示。
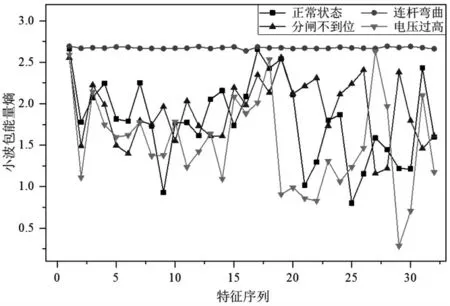
图4 小波包能量熵对比图
由图4可知,连杆弯曲在全区间均与其他3种状态不同;在W1-W16区间,正常状态、分闸不到位、电压过高3种状态变化趋势较为接近,且能量熵值相差不大;而在W16-W32区间,3种状态的小波包能量熵表现出较大差异,有利于分类器对不同状态进行区分。
将小波包能量熵作为SVM的输入向量来验证故障诊断模型的性能。经过多次尝试和对比,采用RBF函数作为SVM的核函数,采用网格寻优算法确定每种特征量的最佳参数,取100组正常信号、6组连杆弯曲信号、4组分闸不到位和电压过高信号作为训练集,剩余数据作为测试集,最终得到3种特征量的SVM分类结果均如图5所示。其中分类标签1-4分别代表正常信号、连杆弯曲、分闸不到位和电压过高。从图5中可以看出,SVM分类结果为100%。由此可见,小波包能量熵和SVM可以用于电磁斥力机构的故障诊断,并取得了较好的结果。
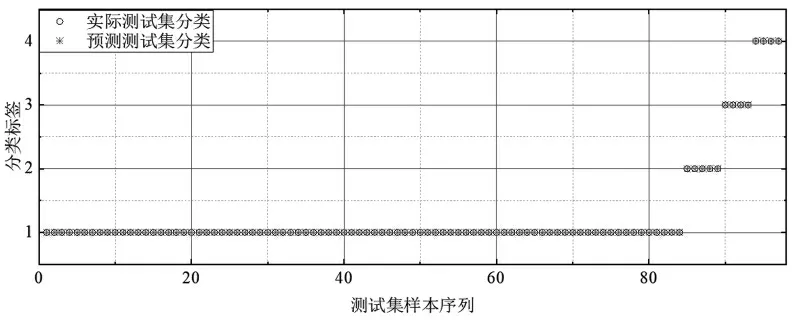
图5 3种特征量的SVM分类结果
3 结束语
本文首先介绍了电磁斥力机构的应用背景和现状,说明了对其进行故障诊断的必要性,并对其基本结构和工作原理进行了详细阐述,然后对目前断路器故障诊断领域的研究现状进行了简要概括,详细介绍了小波包分解和SVM的计算原理,最后应用小波包能量熵和SVM对电磁斥力机构进行了故障诊断,主要得到了以下结论。
(1)在故障限流器和直流断路器等领域,对开关的分闸速度有非常高的要求,电磁斥力机构因此得到了应用,然而相比弹簧操动机构更容易出现故障。因此,需要对故障限流器和直流断路器中的电磁斥力机构进行故障诊断,以预防电力系统事故的发生。
(2)测量振动信号可以获得整个电磁斥力机构的状态信息,目前在状态监测和故障诊断领域已有广泛的应用。特征提取方面,目前使用较多的是小波包分解,SVM由于其在样本数较少的情况下,也可以达到较高的模型准确率,在故障诊断领域得到了广泛的应用。
(3)采用持续监测某样机中电磁斥力机构寿命试验的方法,获得了实际出现的3种故障信号,将小波包能量熵作为SVM的输入向量最终得到SVM分类准确率为100%。由此可见,小波包能量熵和SVM可以用于电磁斥力机构的故障诊断,并取得了较好的结果。
