Analysis and improvement of verifiable blind quantum computation

Min Xiao(肖敏) and Yannan Zhang(张艳南)

1College of Computer Science and Technology,Chongqing University of Posts and Telecommunications,Chongqing 400065,China

2Chongqing Key Laboratory of Cyberspace and Information Security,Chongqing University of Posts and Telecommunications,Chongqing 400065,China

Keywords: verifiable blind quantum computation,universal blind quantum computation,measurement-based quantum computation

1. Introduction

Great progress has been made in quantum computer research,but a quantum state is so sensitive to the environment that any slight change can induce a decoherence effect on it.Hence,costly and sophisticated instruments are needed to ensure the stability of the quantum state. A long-term process is needed to realize the popularization of quantum computers as well as classical computers. It is of great practical significance to build a quantum computing server,which can provide cheap and convenient quantum computing services to ordinary users through remote delegation. Blind quantum computation (BQC)allows the client’s inputs, algorithms and outputs to be secret to the server, which satisfies the client’s privacy requirements. In existing research, the requirements for the client’s quantum computation capabilities are contingent on BQC models,and making the client as classical as possible is the main development direction. The measurement-only BQC model[4]requires the client to be capable of quantum measurement and accessing quantum channels,the universal BQC model[5]requires the client to be able to prepare single qubits and access the quantum channel,and the multiple-server BQC model[6,7]based on this model can realize the target of the client being completely classical.

Considering actual computation experiments, the results may be incorrect due to the dishonesty of the computation environment or the server; the verifiable BQC protocol enables the client to verify the computation results of the server. Existing studies have explored both the verification of BQC with the quantum measurement capability of the client[8–11]and the verification of the universal BQC.[12–14]

In 2005, Childs[15]proposed the first BQC protocol,based on the quantum circuit model. The quantum states in the protocol are encrypted by one-time pads, and the client should qualify for quantum storage and quantum swap gate execution. In 2006, Arrighi and Salvail[16]proposed a BQC protocol that only requires the user to prepare and measure entangled states, which reduces the requirements of the client’s quantum capability. Nonetheless, the protocol just computes certain classical functions,which is not a universal BQC protocol.

In 2009,based on the measurement-based quantum computation model, Broadbentet al.[5]proposed the first universal BQC protocol, which requires the client to prepare single qubits and access the quantum channel. According to the qubits sent by the client, the server constructs the resource state(brickwork state)for computation,and then measures the qubits of the brickwork state and completes the computation under the control of the client. To further reduce the quantum capability requirements of the client and make the client as classical as possible,Morimae and Fuji[6]proposed a doubleserver BQC protocol that only requires the client to access the quantum channels, but the two servers cannot intercommunicate,ensuring the security of the protocol. To address this issue,Liet al.[7]proposed a three-server BQC protocol. Using entanglement swapping technology,users just need to have the capacity to access quantum channels,and the three servers can directly communicate with each other. Nevertheless, the protocol requires three quantum servers and corresponding interactions between them,so the implementation of quantum computation is still hard. Therefore,Xuet al.[17]proposed universal single-server BQC for classical clients in 2014. In 2013,Morimae and Fuji[4]proposed a measurement-only BQC protocol. In this protocol,the preparation of qubits is outsourced to the server, and the specific computation is completed by the client. Compared with the common multiple-server BQC model,the client needs to have more quantum capabilities.

BQC has been verified by experiments in some studies.In 2011,Barzet al.[18]first elaborated the experimental demonstration of blind quantum computing. They demonstrated a variety of blind delegate computations,including one and two qubit gates and the Deutsch and Grover algorithms. It is noteworthy that the experiment is the first step towards unconditionally secure quantum computing in client–server environments. In 2013,Fitzsimonset al.[19]proposed the first experimental verification of verifiable universal BQC. It theoretically indicates how a verifier with the least quantum resources can test a quantum computer and experimentally demonstrates the protocol with four photon qubits. In 2016, Gregantiet al.[20]utilized photonic devices to generate four-qubit cluster states, and experimentally proved the results of computation and verification of a measurement-only BQC protocol.In 2017, Huanget al.[21]implemented a proof-of-principle experiment for completely classical clients. All BQC experiments before this protocol require the client to have weak quantum capabilities. However, this experiment proves the feasibility of a completely classical client performing secure computing on a quantum computation server by experiments,which has a significant bearing on secure cloud quantum computing.

In practice, the correctness of BQC may be affected by diverse factors, such as channel noise, server dishonesty and device error. There are two main techniques to solve the above problems in the current research. One is to adopt logic qubits with fault tolerance or error correction capabilities as basic quantum computation resources,like fault-tolerant codes DF states[22,23]or quantum error-correcting codes.[5,24,25]This method largely aims at the influence of environmental noise in quantum computation. Another way is to insert special qubits for detection in the computation graph and exploit the computation results of these qubits to verify the correctness of the overall computation results,so as to discover the dishonesty of the server with a certain probability.

In 2014,Morimae[4]proposed a verifiable BQC protocol for the measurement-only BQC model. The server prepared the RHG state[26]as the verifiable computation graph state,and the client measured all the qubits and judged whether the server was honest in light of the measurement results of the trap qubits. In 2015,the verifiable BQC protocol proposed by Hayashi and Morimae[9]did not utilize trap qubits. The protocol asked the server Bob to generate a copy of the graph state for BQC, and each qubit was sent to the client Alice in turn.Alice verified the stabilizer[10]of the graph state copy to determine whether Bob had sent the correct graph state, to finally determine whether Bob was honest.

For the universal BQC model,Fitzsimons and Kashefi[12]proposed an unconditionally verifiable universal BQC protocol(FK protocol)in 2015, and introduced the cylinder brickwork state and the dotted-complete graph state as the new computation resource state. In addition to computation qubits,the computation resource state also includes the dummy qubits and the trap qubits, which eliminates the entanglement between the computation qubits and the trap qubits by the dummy qubits, so that each trap qubit has a certain measurement result through the verification of the measurement results of trap qubits,realizing the detection of the server’s computation. In 2017, Kashefi and Wallden[13]improved the above protocol and designed an optimization scheme with fewer quantum resources(KW protocol). In 2020,Xuet al.[14]further improved the construction method of the verifiable computation graph state(XTH protocol), which reduces quantum resources and realizes a lower probability of accepting an incorrect computation result. However,its coloring scheme has limitations,and the probability of accepting incorrect computation results remains at a high level.In this paper,we improve this work to compensate for the deficiencies of the original scheme and further reduce the probability of accepting incorrect computation results. The number of required qubits is the same as for the XTH protocol,while the probability of accepting the wrong computation result is reduced from the original minimum (0.866)d*to (0.819)d*, whered*is the number of repeated execution of the protocol.

The rest of this paper is organized as follows. In Section 2,we introduce and analyze the existing verifiable universal BQC protocols. In Section 3, the limitations of the existing schemes are analyzed and our improvement protocol is put forward. Finally,a summary is given in Section 4.

2. Verifiable universal BQC protocols

Suppose that the client is Alice and the server is Bob in BQC.To introduce trap qubits as detectors in the computation graph state is the main inspiration to realize the verifiability of the computation results. The position and state of these trap qubits are unknown to Bob, so Bob cannot interfere with the actual quantum computation while keeping the trap qubits unaffected.

2.1. Preliminaries

2.1.1. The operation of adding vertices

The operation of adding a vertex to each edge of a graphGis denoted as～(G). The graphGafter performing the～(G)operation is called the dotted graph, which is denoted as ～G.The newly added vertices are called the added vertices, and the set of added vertices is denoted asA(～G). The original vertices are called the primary vertices, and the set of primary vertices is denoted asP(～G).

Figure 1 shows the complete graphK4and the dottedcomplete graph ～K4with four vertices,|A(～K4)|=6,|P(～K4)|=4.

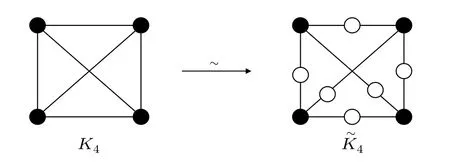
Fig.1. Complete graph K4 and the corresponding dotted-complete graph ～K4.

In the verifiable universal BQC protocol,the computation is mainly performed by designing the graph state with a verification function. In the following description, we utilize the graph language to express the designing idea of the computation graph state,and then utilize the graph state in the specific computation process.

2.1.2. Types of qubits in the computation graph

Computation qubits This refers to the qubits that perform the actual quantum computation in the computation graph state.

Trap qubits This refers to the qubits in the computation graph state to verify the correctness of the computation results.

Dummy qubits This refers to the qubits that are not entangled with any qubit in the computation graph state.Dummy qubits are randomly in|0〉or|1〉. The controlled phase reversal CZ operation does not entangle the qubits in|0〉or|1〉with other qubits. In a graph with a verification function, all the qubits on the adjacent vertex positions of the trap qubits are dummy qubits,which makes the trap qubits unentangled with the computation qubits in the graph state. Accordingly, the measurement of the computation qubits does not impact the trap qubits, and each trap qubit has an explicit measurement result.

2.2. FK protocol[12] based on the dotted-complete graph state

2.2.1. Overview

This scheme utilizes a dotted-complete graph state as the resource state,the author proves it can realize universal quantum computation via performing single-qubit measurement on dotted-complete graph state. The dotted-complete graph state contains redundant qubits(trap qubits and dummy qubits),so as to perform the verification function. According to its own computation task,Alice designs a dotted-complete graph state,determines the positions of computation qubits, trap qubits and dummy qubits and their corresponding series of measurements,and next prepares corresponding single qubits(dummy qubits are in|0〉or|1〉at random, while other qubits are in|+θ〉at random,whereθ ∈{π/4,...,7π/4}). Bob performs controlled phase reversal CZ operation on these qubits to generate a dotted-complete graph state,and then performs a series of measurements specified by Alice on this graph state to complete computation and verification.

2.2.2. Construction of dotted-complete graph state with verification function

(I)Alice selects the security parameterdand transforms the quantum circuit into a series of single qubit measurements on theN-vertices fault-tolerant graph state|GL〉,so as to confirm that the graph state designed for computation ought to be a dotted-complete graph state|˜K3N〉with 3Nprimary vertices.

(II) Alice determines the position of the computation qubits, trap qubits and dummy qubits in the graph state and their corresponding series of measurements in the graph state in the following ways:

(i)The primary vertices of the dotted-complete graph corresponding to the graph|˜K3N〉are randomly selected as a set of three primary verticesP1,P2,P3. The qubits,which are located at the added vertex between any two primary vertices belonging to different primary vertex sets, are selected as dummy qubits. The remaining qubits form three separate primary vertices sets of the dotted-complete subgraph stateP1,P2,P3, denoted as ˜KP1, ˜KP2, ˜KP3.

(ii)One of the three subgraph states is randomly selected as the graph state to perform the computation task. The qubits at the primary vertex positions are all computation qubits,and the qubits at the other positions are dummy qubits. The computation on the graph state|GL〉is realized by performing the measurement operation.The other two subgraph states are utilized solely for verification. The qubits at the primary vertex(or added vertex) positions are taken as trap qubits, and the surplus of qubits at the added vertex(or primary vertex)positions are dummy qubits.

For Bob,the positions of computation qubits,trap qubits and dummy qubits are entirely random. Therefore,the verification to the server can be implemented.

2.2.3. Performance index

The authors define“ε-verifiable”to measure the verification ability of the verifiable universal BQC protocol.

Definition 1 A verifiable BQC protocol is“ε-verifiable”,which means that the upper bound of the probability of Alice accepting incorrect results isε.

For the computation executed on theN-qubits graph state, the scheme needs 3N(3N+1)/2 qubits, which realizes“(2/3)「2d/5-verifiable”,wheredis a security parameter,representing the distance of error correcting code used in the FK protocol.

2.3. KW protocol[13]

Intending to cut down the resource state expenditure of the FK protocol, the KW protocol propounds a new graph state,the dotted triple-graph state,to execute computation and verification.

2.3.1. Dotted triple-graph

As shown in Fig.2,the construction method of the dotted triple-graph is as follows:

(i)A base graphGis given,where verticesv ∈V(G)and edgese ∈E(G),as shown in Fig.2(a).

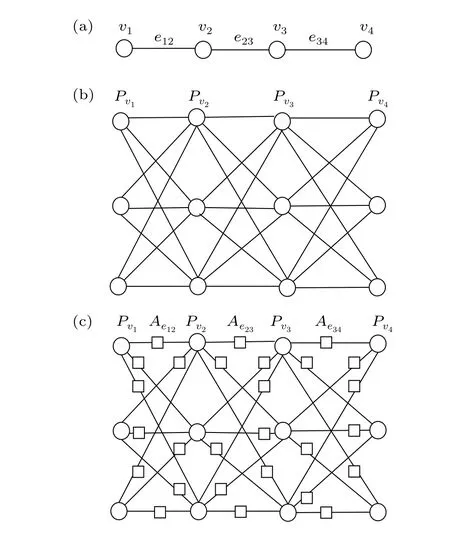
Fig.2. Construction of DT(G).

(iii) For each edgee(vi,vj)∈E(G) connecting two verticesvi,vj(i/=j), a set containing nine edges is defined to connect each vertex inPviandPvj.

(iv)The graph obtained according to step(ii)and step(iii)is the triple graphT(G),as shown in Fig.2(b).

(v) The dotting operation is executed onT(G), and the added vertices are denoted asAewith squares. Finally, the dotted triple-graphDT(G)is obtained,as shown in Fig.2(c).

2.3.2. Construction of dotted triple-graph state with verifiable

Similar to the FK protocol, Alice sets the trap qubits and dummy qubits in the computation dotted triple-graph state|DT(G)〉,prepares the corresponding qubits and performs specific measurements to realize the verification function. Alice selects the computation qubits,trap qubits and dummy qubits by designing the coloring scheme.

(I) A coloring scheme is designed for the dotted triplegraphDT(G). Assuming that the color set is{green, white,red,black},the method is as follows:

(i) The color of each primary vertex inDT(G) is randomly determined to be white, black or green, and the colors of the three vertices in each primary vertex set vary from one to another,as shown in Fig.3(a).

(ii)The color of each added vertex is determined in light of the primary vertex color. The specific rules are as follows:if the color of the two primary vertices adjacent to the added vertex are the same, then the added vertex is colored as the primary vertex; otherwise,the added vertex is colored as red,as shown in Fig.3(b).

(II) According to the coloring scheme, Alice determines the position of computation qubits, trap qubits and dummy qubits.

(i)According to the coloring scheme of the dotted triplegraphDT(G),Alice chooses the red qubits of added vertex positions as dummy qubits,and the remaining qubits form three subgraph states which are the same as the dotted triple-graph state|DT(G)〉of the basic graph state|G〉. Each subgraph state contains only one color and the color is definitely disparate as shown in Fig.3(c).

(ii) Alice randomly selects one of the three subgraph states as the graph state to perform the computation task. The other two subgraph states are utilized solely for verification.The qubits at the primary vertices(or added vertices)are taken as trap qubits, and the remaining qubits at the added vertices(or primary vertices)are dummy qubits,as shown in Fig.3(d).

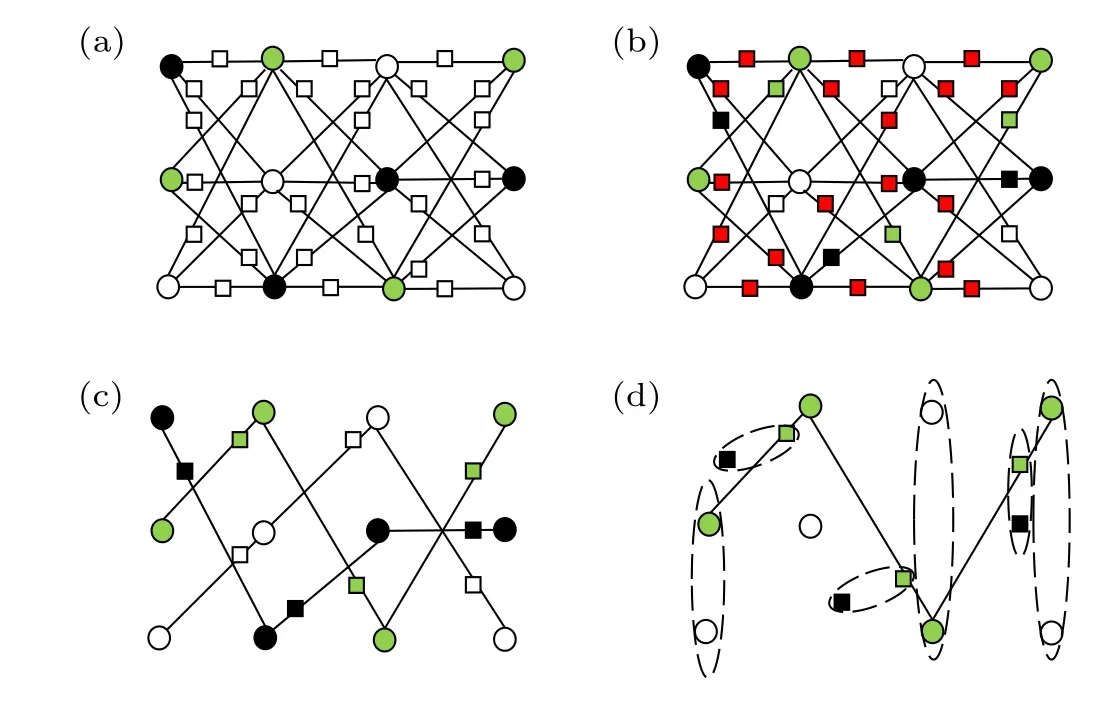
Fig.3. Coloring and break operations of DT(G).

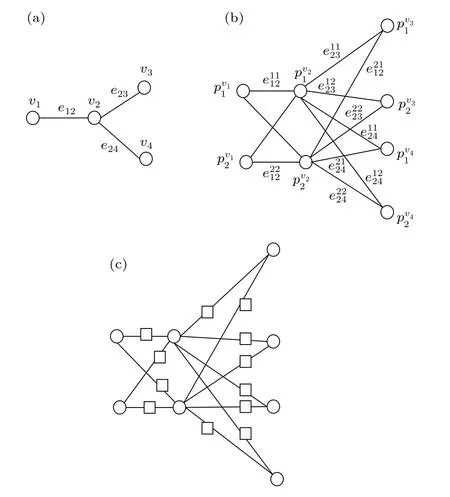
Fig.4. Construction of S(G).

2.3.3. Performance index

The number of vertices of the dotted triple-graphDT(G)designed by this protocol is|V(DT(G))|=3|V(G)|+9|E(G)|,where|V(G)|=Nand|E(G)|≤cN;cis the maximum degree of the vertices of the base graphG,which is a constant. Compared with the FK protocol, the cost of the resource state is reduced from quadraticO(N2)to linearO(N). The KW protocol realizes“8/9≈0.899-verifiable”. Aimed at enhancing the verification ability,the scheme proposes that the protocol can be implemented “0.899d*-verifiable” by executing the same computation task multiple times, whered*is the number of repeated executions of the protocol.

2.4. XTH protocol[14]

On behalf of further decreasing the resource state expenditure and enhancing the verification capability of KW protocol, the XTH protocol exploits utilization of the graph state corresponding to the sandglass-like graph to perform computation.

2.4.1. Sandglass-like graph

As shown in Fig. 4, the construction method of the sandglass-like graph is as follows:

(i) They are given a base graphG, where verticesv ∈V(G)and edgese ∈E(G),as shown in Fig.4(a).

(v) The dotting operation is executed onI(G), and the added vertices are denoted asAewith squares. Finally, the sandglass-like graphS(G)is obtained,as shown in Fig.4(c).

2.4.2. Construction of sandglass-like graph state with verifiable

Similar to the KW protocol, Alice chooses the computation qubits, trap qubits and dummy qubits by designing the coloring scheme on the sandglass-like graph state.

(I) A coloring scheme is designed for the sandglass-like graphS(G).Assuming that the color set is{green,white,red},the method is as follows:

(i)In each primary vertex set,one vertex is randomly selected to be colored green,and the remaining vertex is colored red with a probability ofαand white with a probability of 1-α,whereαis a constant.

(ii) The color of the added vertex is determined in light of the primary vertex color. The specific rules are as follows:if the colors of the two adjacent primary vertices are different,the added vertex is colored white;if the two primary vertices adjacent to the added vertex are green, the added vertex is colored green; and if the two primary vertices adjacent to the added vertex are white,the added vertex is colored red,as shown in Fig.5(a).

(II) According to the coloring scheme, Alice determines the position of computation qubits, trap qubits and dummy qubits.

According to the coloring scheme of the sandglass-like graphS(G), Alice selects the qubits at the white vertices as the dummy qubits,and the remaining qubits form a subgraph state which is the same as the dotted graph state|D(G)〉of the basic graph state|G〉and some qubits which are not entangled with any qubit(corresponding to the red vertex positions).The subgraph state is utilized as the graph state to perform the computation task,and the qubits at the red vertices are utilized as trap qubits,as shown in Fig.5(b).

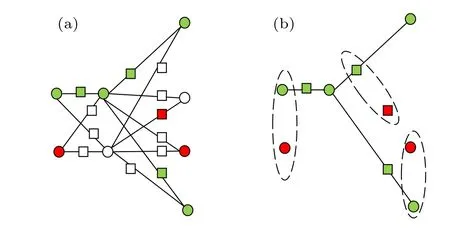
Fig.5. Coloring and break operations of S(G).

2.4.3. Performance index

The number of vertices of the sandglass-like graphS(G)designed by this protocol is|V(S(G))|=2|V(G)|+4|E(G)|,where|V(G)|=Nand|E(G)|≤cN;cis the maximum degree of the vertices of the base graphG, which is a constant.Compared with the KW protocol, the cost of the resource state is further reduced. The XTH protocol realizes “0.866-verifiable”. In order to further improve the verification capability,the method of multiple execution of the same computation task proposed by the FK protocol is adopted to finally realize“(0.866)d*-verifiable”,andd*is the number of repeated executions of the protocol.

3. Improvement of the XTH protocol

3.1. Limitations of coloring scheme in XTH protocol

Although the XTH protocol utilizes fewer resources to improve the KW protocol and realize the verification of the computation results of the BQC server, the protocol still has the following problems.

According to the coloring scheme,the color set of any primary vertex set is{green, white}or{green, red}. There are edges between any two vertices belonging to different vertex sets in the sandglass-like graph, which means that there exist added vertices. Hence,the colors of the two primary vertices adjacent to any added vertex may be different, or they may both be green,white,or red.

(i) The coloring scheme does not consider how to color the added vertices when the two primary vertices are both red.The situation is that if there are two adjacent primary vertices whose colors are red,it would not take the corresponding qubits of added vertex positions into account in the subsequent computation. If the qubits at these positions are simply selected as dummy qubits,the trap qubits in the final graph state will only contain the primary vertices without added vertices,as shown in Fig.6. If the server’s dishonesty acts on the qubits of added vertex positions,the client can not detect it.

(ii) The coloring scheme may result in no red vertices in all the primary vertices; after selecting white vertices as dummy qubits,the trap qubits in the final graph state only include added vertices but no primary vertices. If the server’s dishonesty acts on the qubits of primary vertex positions, the client cannot detect it. This protocol adopts the resource state of the XTH protocol. A new coloring scheme for the sandglass-like graphS(G)is designed,which solves the problem of coloring limitations in the XTH protocol and further improves the detection ability.

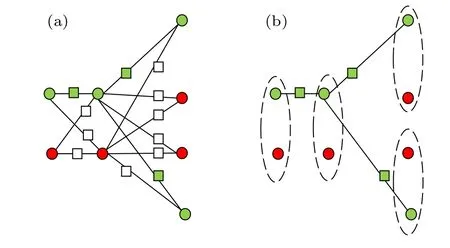
Fig.6. An example of coloring limitation in XTH protocol.

3.2. Improved coloring scheme

(i)The color set of primary vertices is{red,green,blue}.In each primary vertex set,one vertex is randomly selected to be colored green,and the remaining vertex is colored red with a probability ofαand blue with a probability of 1-α,whereα ∈(0,1)is a constant.

(ii) The color set of the added vertices is{white, red,green,blue}. The colors of the added vertices are determined in light of the primary vertex color. The rules are as follows.

If the colors of the two primary vertices adjacent to the added vertex are different, the added vertex will be colored white;if the two primary vertices adjacent to the added vertex are green, the added vertex is colored green; if the two primary vertices adjacent to the added vertex are red, the added vertex is colored blue;and if the two primary vertices adjacent to the added vertex are blue, the added vertex is colored red,as shown in Figs.7(a)and 8(a).

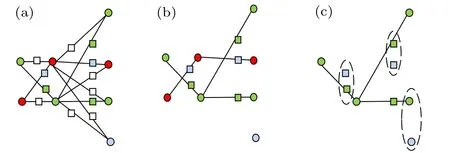
Fig.7. Improved coloring scheme 1 of S(G).

3.3. Determination of computation qubits,dummy qubits,

and trap qubits

According to the above coloring scheme,the client selects the qubits at the white vertex positions as the dummy qubits.The remaining qubits form a subgraph state which is the same as the dotted graph state|D(G)〉of the basic graph state|G)〉,a subgraph state composed of red and blue vertices,and some qubits which are not entangled with any qubit, as shown in Figs.7(b)and 8(b).

When the number of blue vertices is no less than that of red vertices: The qubits at the red vertices are selected as the dummy qubits. All the qubits that are not entangled with any qubits in the graph state are taken as the trap qubits, and the subgraph state that is the same as the dotted graph state|D(G)〉is taken as the computation graph state to perform the computation task, in which all the qubits are computation qubits, as shown in Fig.7(c).

When the number of red vertices is more than that of blue vertices: The qubits at the blue vertices are selected as the dummy qubits. All the qubits that are not entangled with any qubits in the graph state are taken as the trap qubits, and the subgraph state that is the same as the dotted graph state|D(G)〉is taken as the computation graph state to perform the computation task, in which all the qubits are computation qubits, as shown in Fig.8(c).

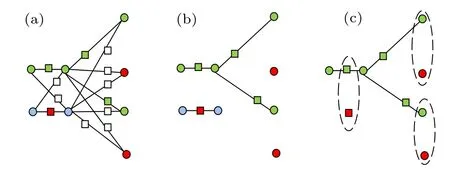
Fig.8. Improved coloring scheme 2 of S(G).

3.4. Implementation of the protocol

The implementation of the protocol is divided into preparation phase, computation phase and verification phase. We assume that the client in our protocol is Alice, and the server is Bob.

3.4.1. Preparation phase

(i) Alice designs the sandglass-like graphS(G) according to the computation task and randomly selects a coloring scheme satisfying the following conditions, then determines the position of the computation qubits,dummy qubits and trap qubits in the sandglass-like graphS(G):

When coloring,in order to determine the position of trap qubits in the final graph state both in the primary vertex set and in the added vertex set, Alice randomly selects a coloring scheme to ensure that the colors of primary vertices in the coloring scheme include three colors,and simultaneously,the number of blue vertices is no less than that of red vertices,which notably makes the detection rate of the scheme higher.Otherwise, another coloring scheme satisfying this condition is selected again.

(ii) Alice records the sequence of measurement angles on each qubit, whereφ= (φi)1≤i≤(2N+4cN)andφi ∈A ≡{0,π/4,...,7π/4}; for all the trap qubits and dummy qubits,φi=0.

(iii) Alice prepares a binary stringsof length 2N+4cNwith all initial values of 0,which is utilized to record the measurement results of each qubit.

(iv) Alice records the random valuesθi,ri,di,xicorresponding to qubiti,whereθi ∈A,ri,di,xi ∈{0,1}.

(v) Alice prepares the qubits needed for the sandglasslike graph state|S(G)〉. If the qubit is a dummy qubit, it is prepared as|di〉,otherwise it is ∏j∈NG(i)∩D Zdj|+θi〉,whereDis the set of all dummy qubits in the graph state|S(G)〉, andNG(i) is the set of all adjacent vertices of vertexiin graphS(G). Bob utilizes controlled phase reversal CZ operation to prepare a sandglass-like graph state for the received qubits.

3.4.2. Computation phase

(i) Alice computes the measurement angleδi=C(i,φi,θi,ri,s)of each qubit, and sends the measurement angle to Bob;if qubitiis a dummy qubit,thenφi=θi+riπ.

(ii)Bob utilizes basis|±δi〉to measure qubiti,and then sends the measurement resultbito Alice.

(iii)Alice modifies the value ofsiinstobi ⊕ri.

(iv)The above steps are repeated until the computation is completed.

(v)Bob sends the computation result to Alice.

3.4.3. Verification phase

Alice verifies the measurement results of trap qubits. For the measurement resultbtof each trap qubit, ifbt=rtis satisfied,Bob is proven to be honest,and Alice accepts the computation results;otherwise,Alice judges that Bob is dishonest and refuses the computation.

3.5. Protocol analysis

3.5.1. Blindness and correctness analysis

The blindness and correctness are similar to the XTH protocol.

For the blindness,because the positions of all trap qubits and dummy qubits in the computation graph state are unknown to Bob,the protocol satisfies blindness.

For correctness,we have designed a new coloring scheme to determine the position of each qubit in the computation graph state. Two independent computation and trap subgraphs can be obtained by measuring the dummy qubits in the computation graph state. The computation subgraph is used to perform the computation function similar to the universal BQC protocol. Each qubit in the trap subgraph can obtain a deterministic computation measurement result if the server executes the measurement honestly. Therefore, the correctness of the computation subgraph comes from the correctness of the universal BQC protocol, and the correctness of the trap subgraph comes from the deterministic computation results of each trap qubit. Hence,the protocol satisfies correctness.

3.5.2. Verifiability analysis

According to the structure and coloring of the resource state,for any non-output primary vertex set,the color set is{green,red,white}with the probability of(1-α)2(the qubits corresponding to the vertices in the added vertex set are composed of computation qubits, trap qubits and dummy qubits), and the probability of 1-(1-α)2is{green, white}(the qubits corresponding to the vertices in the added vertex set are composed of computation qubits and dummy qubits)and|Aeβ|=4.ε=max{(1/2)+(1/2)α,(3/4)+(1/2)α-(1/4)α2}.

If there are more red vertices than blue vertices in the selected coloring scheme,then whenαis infinitely close to 1,εwill also be infinitely close to 1,which greatly reduces the detection rate of the scheme. Therefore,for the coloring scheme,only the scheme with no less blue vertices than red ones is selected.

However, whenαis infinitely close to 1, the probability that the number of blue vertices in the coloring scheme is no less than the number of red vertices is relatively low,so combining the two cases, choosingα= 0.85, thenε=max{0.575,0.819}=0.819.

This scheme does not consider non-trivial attack acts on the output primary vertex qubits. Since the main focus of this solution is to achieve verifiable BQC without adding additional client quantum capabilities, non-trivial attacks acting on the output of the primary vertex qubits mean that the computation output is a quantum output, and the client needs to measure the output qubits. Quantum measurement will undoubtedly increase the quantum capability requirements of the client.

Therefore,the maximum probability that Alice accepts an incorrect computation result in this scheme isε=0.819.

In order to reduce the probability of Alice accepting an incorrect computation result, repetition technology similar to the KW and XTH protocols is adopted. Diverse random parameters are selected for each repetition. For the same computation, each repetition will have the same computation result.Therefore,the maximum probability of Alice accepting an incorrect result is“(0.819)d*-verifiable”,whered*is the number of repetitions.

3.5.3. Comparison with existing protocols

Table 1 shows the comparison between the proposed protocol and the existing work(FK protocol,KW protocol,XTH protocol)in terms of the required resource state cost and verifiability index. The results show that the proposed protocol compensates for the existing protocol limitations and improves the verification ability.

Table 1. Comparison of cost and verification capability of verifiable BQC scheme.

4. Conclusion

BQC is of great significance to the application of quantum computation in practice. In this paper, the existing verifiable universal BQC protocols are analyzed and compared in detail.The limitations of existing protocols are corrected and the verification capability is markedly improved. Generally speaking,the verification ability of the protocols in the research needs further improvement,and the quantum capability of the client needs further reduction.In the future,the verifiability of multiserver universal BQC with the classical clients can be considered. Ref.[27]summarizes various challenges and future development directions in the field of verifiable BQC, such as significant reduction of the overhead and noise sensitivity,and verification of quantum simulators and other special-purpose devices,which provides guidance for future research.