Analysis on vibration characteristics of large-size rectangular piezoelectric composite plate based on quasi-periodic phononic crystal structure

Li-Qing Hu(胡理情), Sha Wang(王莎), and Shu-Yu Lin(林书玉)

Shaanxi Key Laboratory of Ultrasonics,Institute of Applied Acoustics,Shaanxi Normal University,Xi’an 710119,China

Keywords: composite materials,rectangular piezoelectric plate,coupled vibration,band gap

1. Introduction

Piezoelectric ceramic transducers are widely used in high-power ultrasonic and underwater acoustic fields. In order to improve the performance of transducers, many scholars combine piezoelectric materials with polymer materials to expand the advantages of materials.[1–7]It is found that the strength and brittleness of the ceramics can be effectively reduced by adjusting the volume ratio and mass ratio of the material.The transverse coupling of the ceramics can be reduced,the longitudinal electromechanical conversion efficiency of the composite can be increased, and the composite also has wide bandwidth,low acoustic impedance,and easy impedance matching with water, skin, and other media.[8–10]As a functional material with periodic structure,PC is also composed of two kinds of materials,and because of their band gap and passband characteristics,in recent years,many scholars have studied their applications in noise reduction and vibration reduction of acoustic transducers.[11–14]Konget al.[15]and Ahmedet al.[16]have shown that the existence and width of a complete band gap can be adjusted by adding a defect state into the PC structure,thereby changing the filling rate of the scatterer,the temperature,etc. Based on their bandgap characteristics, the PCs have been widely used in vibration suppression. Shaoet al. applied the PC of honeycomb structure to low-frequency vibration reduction. The effects of plate thickness, column height, and column radius are analyzed. It has been found that the amplitude of the vibrating plate can be significantly reduced under the optimal size.[17]Wilmet al.used the plane wave expansion method to obtain the dispersion curves of the wave propagating in the composites by considering the piezoelectric effect,the acoustic loss,and the electric excitation.[18]Silviaet al.[19]and Aragonet al.[20]drilled a periodic cylindrical hole array in the thickness direction of the piezoelectric ceramic and found that the finite-period PC structure has an obvious effect on suppressing the coupled vibration. Several researchers have effectively improved. The large-scale ultrasonic plastic welding system by designing the quasi-periodic PC structure on the front cover plate of the transducer and the tool head, and the uniformity of the displacement distribution on the radiation surface of the front cover was also improved.[21–24]

The characteristics of a piezoelectric ultrasonic transducer are closely related to the material,geometry,and size of the piezoelectric vibrator. The piezoelectric composite plate is the key to the vibration of the transducer,so it is important to study the vibration characteristics of the piezoelectric vibrator. In general,the transverse dimension of a piezoelectric ceramic transducer is less than one-fourth of its wavelength,so the transverse vibration can be neglected. When transducers are used at high frequencies and in applications such as ultrasonic welding, the transverse dimension of transducers needs increasing. The vibration mode of the piezoelectric ceramic transducer is affected by the vibration mode of other dimensions, and the influence of coupled vibration on the transducer cannot be neglected in the theoretical calculation. Otherwise,the frequency error will increase. Therefore,the coupled vibration theory must be used to analyze the vibration of the large-size rectangular composite piezoelectric plate to reduce the error.[25,26]Many scholars have studied the vibration of the piezoelectric ceramic rectangular plates. Jiet al.have studied the two-dimensional (2D) coupled vibration of a rectangular piezoelectric plate,and discussed the correlation between transverse effective electromechanical coupling coefficient and the ratio of length to width. Linet al.[27]used the equivalent elastic method to analyze the three-dimensional(3D)coupled vibration of the piezoelectric ceramic rectangular plate with and without the piezoelectric effect. The 3D equivalent circuit was derived, and the resonant frequency of the piezoelectric vibrator was calculated. It is shown that the theoretical results are in good agreement with the experimental results and can be effective.[28,29]

In the present work,a piezoelectric composite plate composed of piezoelectric ceramics and epoxy is proposed. The structure of PZT-4 and epoxy are analyzed by the theory of PC.A large-size rectangular piezoelectric composite plate model with the quasi-periodic PC structure is presented in Fig.1(a).The length,width,and thickness arel1,l2,andl3. Figure 1(b)shows a protocell of PC.The epoxy resin that is not connected is called scatterer and the side length isa; the PZT-4 connected with the epoxy rasin as a whole is called matrix and the side length isb. The equivalent material parameters of the rectangular piezoelectric composite plate are derived by using the series-parallel connection theory and the uniform field theory proposed by Newnhamet al.[30]The complex coupled vibration of a rectangular piezoelectric composite plate is simplified into the coupling of three one-dimensional(1D)vibrations,and the electromechanical equivalent circuit diagram of the coupled vibration is obtained. According to the resonance frequency equation of coupled vibration, the resonance frequency of three dimensions can be calculated. When the volume fraction of the piezoelectric ceramics is 91%and the volume fraction of the epoxy is 9%,the influence of the thickness,length, and thickness of the rectangular composite piezoelectric composite plate on the resonant frequency and the electromechanical coupling coefficient in different dimensions are studied. The influence of the volume fraction of polymer on the thickness resonance frequency of the transducer is also investigated. The acceleration response curves in theXandYdirections are calculated by the finite element method. The bandgap range of the large-size rectangular piezoelectric composite plate with the quasi-periodic PC structure is calculated.When the volume fraction of the polymer is changed such that the thickness resonance frequency of the rectangular piezoelectric composite plate is in the bandgap range of in theXandYdirections, the transverse vibration can be suppressed effectively. The thickness vibration amplitude increases and the vibrational modes also become purer.

Fig. 1. (a) Diagram of large-size rectangular piezoelectric composite plate with quasi-periodic PC structure. (b)Cell of rectangular PC.

2. Derivation of equivalent material parameters of large-size rectangular piezoelectric plate with quasi-periodic phononic crystal structure

In order to study the vibration characteristics of the largesize rectangular piezoelectric composite plate with the quasiperiodic PC, the effective equivalent parameters of the material need calculating. By using the Smith’s method to analyse the composite materials,the strain and electric field are chosen as the independent coordinates in our analysis.[31]The piezoelectric phase is made of PZT-4, we take it to be poled along thePin Fig.1(a):

Here,subscriptpis used to distinguish the parameters of different materials for the polymer parameters, and subscriptmfor the equivalent parameters of composites;Tis the stress;Sis the strain;Eis the electric field strength;Dis the electric displacement;Cis the elastic stiffness constant;eis the piezoelectric stress constant;εis the dielectric constant.

In theXandYdirections, the piezoelectric phase and the polymer phase are connected in series so that the lateral stresses are equal in both phases, and the lateral strains are calculated according to the volume fraction of the constituent phases,i.e.,T1=TP1=Tm1,Sm1=v1S1+v2SP1,T2=TP2=Tm2, andSm2=v1S2+v2SP2.In theZdirection,the piezoelectric phase and the polymer phase are connected in parallel, and the two phases vibrate together with uniform thickness, so the vertical strain is the same and the stress is calculated according to the volume fraction of the constituent phases,i.e.,Tm3=v1T3+v2TP3andS3=SP3=Sm3. The electric field intensity components are equal,and the electric displacement component is calculated according to the volume fraction of the constituent phases,i.e.,E3=EP3=Em3andDm3=v1D3+v2DP3. Herev1andv2are the volume fractions of the piezoelectric phase and the polymer phase respectively.TheT1,T2,S3,andE3are the independent variables in piezoelectric phase andTP1,TP2,SP3, andEp3are the independent variables in polymer phase. Taking the equal quantities in two phases as independent variables, the constitutive relation can be established as follows:

According to the transformation of Eq.(19),the equivalent parameter matrix can be obtained as follows:

The elastic constant matrix is the inverse of the flexible matrix,we have

3. Vibration analysis of large-size rectangular piezoelectric composite plate with quasiperiodic phononic crystal structure

3.1. Theoretical analysis of three-dimensional coupled vibration of large-size rectangular piezoelectric composite plate with quasi-periodic phononic crystal structure

When theX,Y,andZdimensions of the large-size rectangular piezoelectric composite plate with the quasi-periodic PC structure are comparable to each other, the complex coupling vibration can be formed in the three directions.By introducing 3D mechanical coupling coefficientsn1=T1/T2,n2=T2/T3,andn3=T3/T1,the equivalent circuit diagram of 3D coupled vibration can be obtained as shown in Fig. 2, whereVis the total voltage of the rectangular piezoelectric composite plate,V=V31=V32=V33,whereV31,V31,andV31are the voltages across the two electrodes of the corresponding resonator in the three extensional vibration modes,respectively.

Fig. 2. Electromechanical equivalent circuit of 3D coupled vibration of large-size rectangular piezoelectric composite plate with quasi-periodic PC structure.

In Fig. 2,Zi1,Zi2, andZi3are equivalent mechanical impedances in the three directions(i=1,2,3),I31,I32,andI33are the currents flow into the rectangular piezoelectric plate,the total currentI=I31+I32+I33.

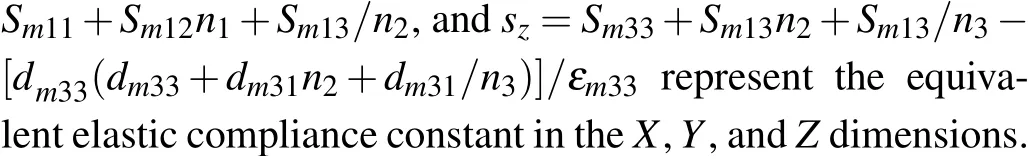
denote the electromechanical conversion coefficient of theX,Y,andZdimensions.

The third equation is clearly a transcendental equation,let Δ=(fa-fr)/fa, wherefrandfaare the resonance frequency and antiresonance frequency in theZdirection respectively.For the fundamental mode,Kz=ω/Vz,Ka=ωa/Vz,and tan(kal3/2)=∞. According to the three frequency equations,the frequency equation of the large-size rectangular piezoelectric composite plate with the quasi-periodic PC structure considering the piezoelectric effect and vibration coupling in different directions can be written as follows:

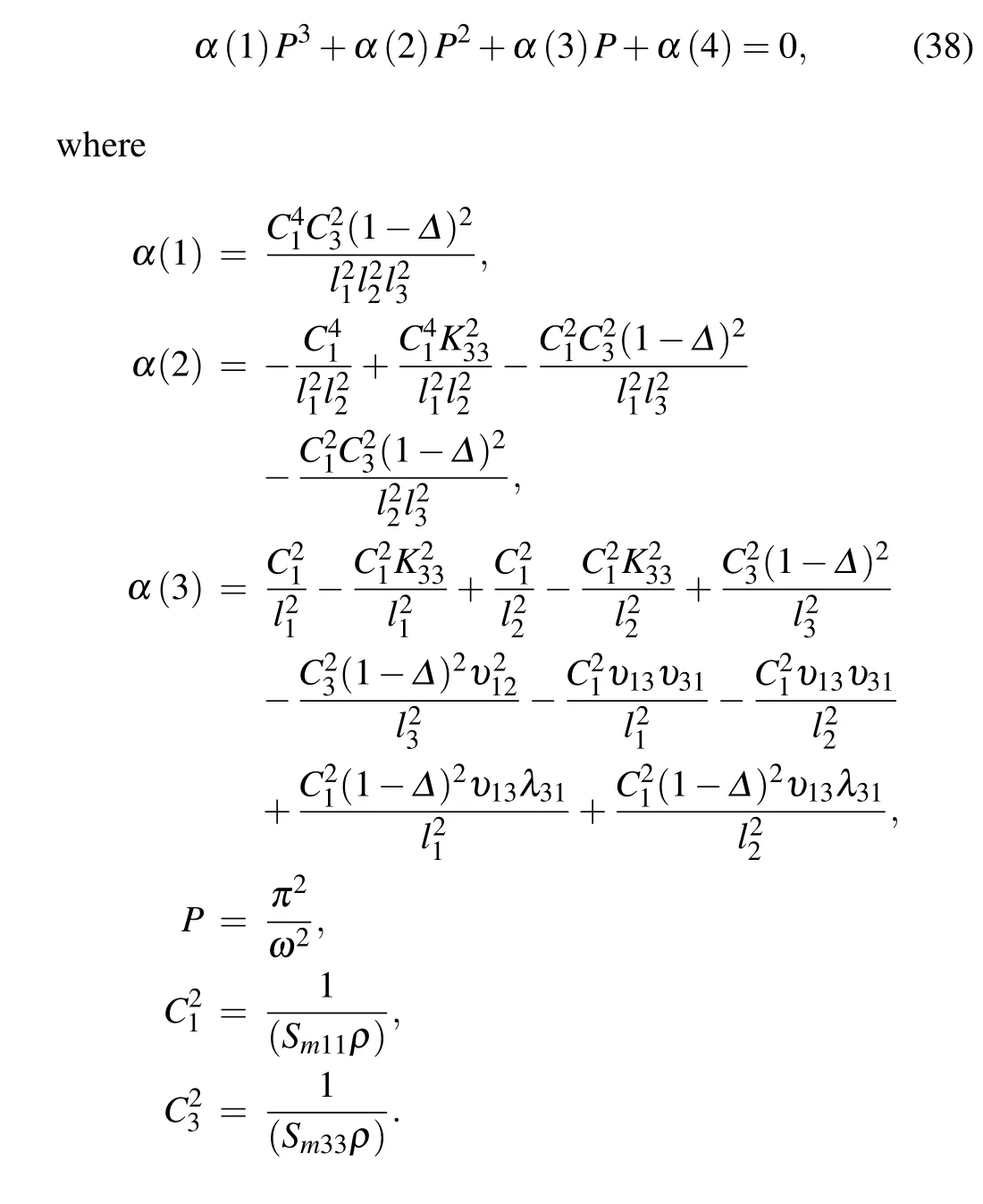
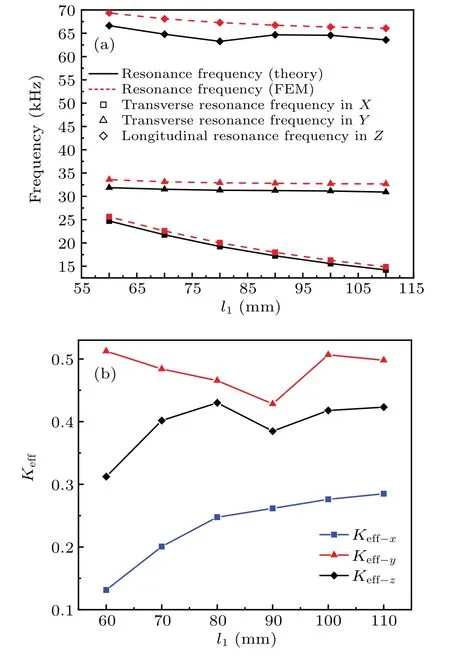
Fig.3. (a)Relationship between resonance frequency and length of rectangular piezoelectric plate. (b)Relationship between effective electromechanical coupling coefficient and length of rectangular piezoelectric plate.

3.2. Influence of size of large-size rectangular piezoelectric composite plate with quasi-periodic phononic crystal structure on its vibration characteristics

The piezoelectric material used in this model is PZT-4,and its material parameters areρ1=7500 kg/m3,C11=13.9×1010m2/N,C12=7.78×1010m2/N,C13=7.43×1010m2/N,C33=11.5×1010m2/N,e31=-5.2 C/m2,e33=15.1 C/m2,ε33/ε0= 1300, andε0= 8.8542×10-12F/m. The polymer is epoxy resin, and its material parameters areCp11=8×1010m2/N,Cp12=4.4×1010m2/N, andεp11=0.037×10-9F/m.The volume fractions of piezoelectric materials and polymers are fixed at 91%and 9%,a=10 mm,andb=3 mm.Wolfram Mathematica 9.0 can be used to calculate the values of equivalent parameters of the large-size rectangular piezoelectric composite plate from Eqs. (20)–(22). The resonance frequencies of the rectangular piezoelectric composite plate in theX,Y,andZdimensions can be obtained by substituting the parameters into Eq.(38).

Figures 3(a)–5(a) respectively illustrate the effect of geometric size on resonant frequency by changing the length,width,and thickness of the piezoelectric plate.The black solid line denotes the resonance frequency curve calculated by the analytical method; the red dotted line refers to the resonance frequency curve calculated by FEM. The square point represents the resonance frequency in theXdirection; the triangle point represents the resonance frequency in theYdirection;the diamond point represents the resonant frequency in theZdirection.As can be seen from Figs.3(a)–5(a),when the width and thickness of the rectangular plate are fixed at 50 mm and 30 mm, respectively, the resonance frequency in theXdirection decreases with the increase of the length of the rectangular plate; the resonance frequency in theYdirection remains almost unchanged; the resonance frequency inZdirection also decreases slowly. When the length and thickness of the rectangular plate are fixed at 100 mm and 30 mm,respectively,the resonance frequency in theYdirection decreases with the increase of the width of the rectangular plate,the resonance frequency in theXdirection remains almost unchanged,and theZdirection resonance frequency decreases slowly. When the length and width of the rectangular plate are fixed at 100 mm and 40 mm, respectively, the resonance frequency in theZdirection decreases with the increase of the thickness of the rectangular plate, the resonance frequency in theYdirection decreases slowly,and theXdirection resonance frequency remains almost unchanged.

The effective electromechanical coupling coefficient of the transducer can be expressed as

wherefrandfarepresent the resonance frequency and antiresonance frequency of the piezoelectric composite plate respectively.Keff-x,Keff-y, andKeff-zrepresent the effective electromechanical coupling coefficients of the piezoelectric rectangular plate in theX,Y, andZdirections, respectively. The effect of geometry on the effective electromechanical coupling coefficient is studied and shown in Figs. 3(b)–5(b). It can be seen that the resonance frequency of the piezoelectric composite plate and the effective electromechanical coupling coefficient can be changed by adjusting the size of the piezoelectric composite plate.

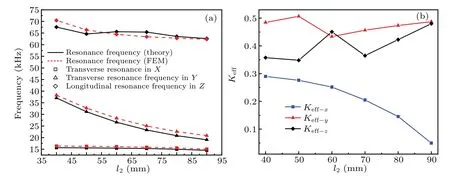
Fig. 4. (a) Relationship between resonance frequency and width of rectangular piezoelectric plate. (b) Relationship between effective electromechanical coupling coefficient and width of rectangular piezoelectric plate.

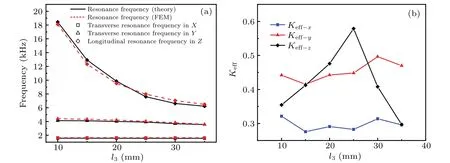
Fig. 5. (a) Relationship between resonant frequency and thickness of rectangular piezoelectric plate. (b) Relationship between effective electromechanical coupling coefficient and thickness of the rectangular piezoelectric plate.

3.3. Influence of volume fraction of scatterer on thickness vibration characteristics of large-size rectangular piezoelectric composite plate with quasi-periodic phononic crystal structure

The volume fraction of the polymer phase, also known as the filling ratio of the scatterer, affects not only the material parameters of the composite piezoelectric composite plate but also the existence and width of the complete band gap of the PC.The lattice period also affects the band gap of the PC.When the vibration frequency is within the band gap range,the propagation of elastic waves can be suppressed or even forbidden. The large-size rectangular piezoelectric composite plate is a typical quasi-periodic 2D PC with the finite periodic structure in theXandYdirections. When the thickness resonance frequency of the piezoelectric composite plate is within the band gap range in theXandYdirections, the transverse vibration can be suppressed and the thickness vibration can be more uniform. The dispersion curve can be used to visualize the band gap properties of PCs. The plane wave expansion method is usually used to calculate the dispersion curve of an ideal 2D PC with infinite period in two dimensions.The quasiperiodic PC structures used in transducers are all finite periodic structures. Based on the characteristic of finite periodic structure, the finite element method can be used to calculate the band gap. The acceleration response curves in theXandYdirections can be obtained by uniformly applying 1-m/s2acceleration to one side and calculating the output response to the other side of the finite-period 2D PC.

The length,width,and thickness of the rectangular piezoelectric composite plate are 100 mm, 40 mm, and 10 mm respectively,ais 10 mm,andbis changed from 2 mm to 5 mm.vis the volume fraction of the scatterer,specificallyv=b2/a2.The relationship between resonance frequency andv, studied by the analytical method and by finite element method, are shown in Fig.6(a). It is obvious that the effective electromechanical coupling coefficient increases to about 0.5 with the increase ofvin Fig. 6(b). Whenb=2 mm, the resonance frequency of the piezoelectric composite plate is 180650 Hz.As shown in Fig. 7(a), it is obvious that its thickness vibration mode is affected by the transverse vibration. The vibration amplitude is small and the mode is chaotic. As shown in Fig. 7(b), when the side length of the scatterer isb=5 mm,the thickness resonance frequency of the large-size rectangular piezoelectric composite plate with the quasi-periodic PC structure is 180910 Hz. The extensional vibration in the thickness direction is more uniform, and the vibration amplitude increases. In this work, the large-size rectangular piezoelectric composite plate with the quasi-periodic PC structure used in transducers possesses a finite-periodic structure. The twodimensional PC structure has a band gap in theXandYdirections, when the thickness resonance frequency is in the band gap,the transverse vibration can be suppressed and the thickness resonance frequency can be affected. From Fig.8,when the side length of the scatterer isb=2 mm the resonance frequency 180650 Hz is not in the transverse band gap; when the side length of the scatterer isb=5 mm, it is noticed that the band gap exists inXdirection varying from 180300 Hz to 181500 Hz and the band gap exists inYdirection varying from 179800 Hz to 183300 Hz near the resonance frequency.The resonance frequency 180910 Hz is in the band gap range of bothXandYdirections,which can effectively suppress the influence of the transverse vibration on the thickness vibration to achieve more uniform thickness vibration. It is shown that the photonic band gap can be adjusted by changing the volume fraction of the scatterer and the period. If the thickness resonance frequency is in the range of the transverse band gap,the coupled vibration of the piezoelectric composite plate can be effectively reduced. The vibration displacement distributions along the length and width of the rectangular piezoelectric composite plate when it vibrates along the thickness direction are drawn. As shown in Fig. 9, whenb=5 mm,the whole vibration is more uniform and the displacement of the whole vibration is obviously increased. When used in ultrasonic transducers,the structure can effectively suppress the transverse vibration of the transducers,and the performance of the transducers can be optimized.

Fig.6. Effect of volume fraction of epoxy on vibration characteristics of the composite piezoelectric plate,showing(a)relationship between thickness resonance frequency and volume fraction of epoxy,and(b)relationship between effective electromechanical coupling coefficient and volume fraction of epoxy.

Fig.7. Longitudinal vibrations of large-size rectangular piezoelectric composite plate with quasi-periodic PC structure in the Z direction for b=2 mm(a)and 5 mm(b).

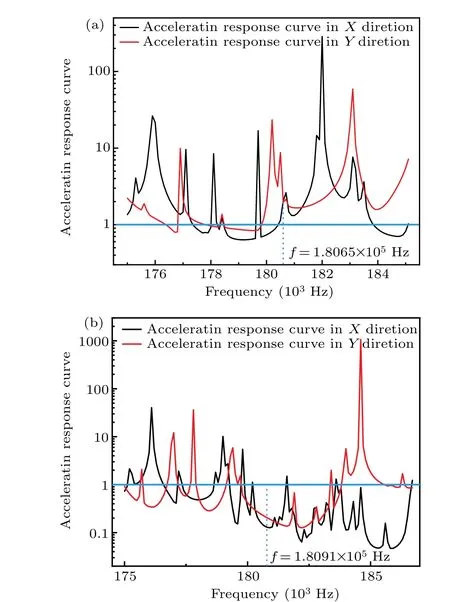
Fig.8. Acceleration response curves of large-size rectangular piezoelectric composite plate with the quasi-periodic PC structure in X and Y directions for b=2 mm(a)and 5 mm(b).

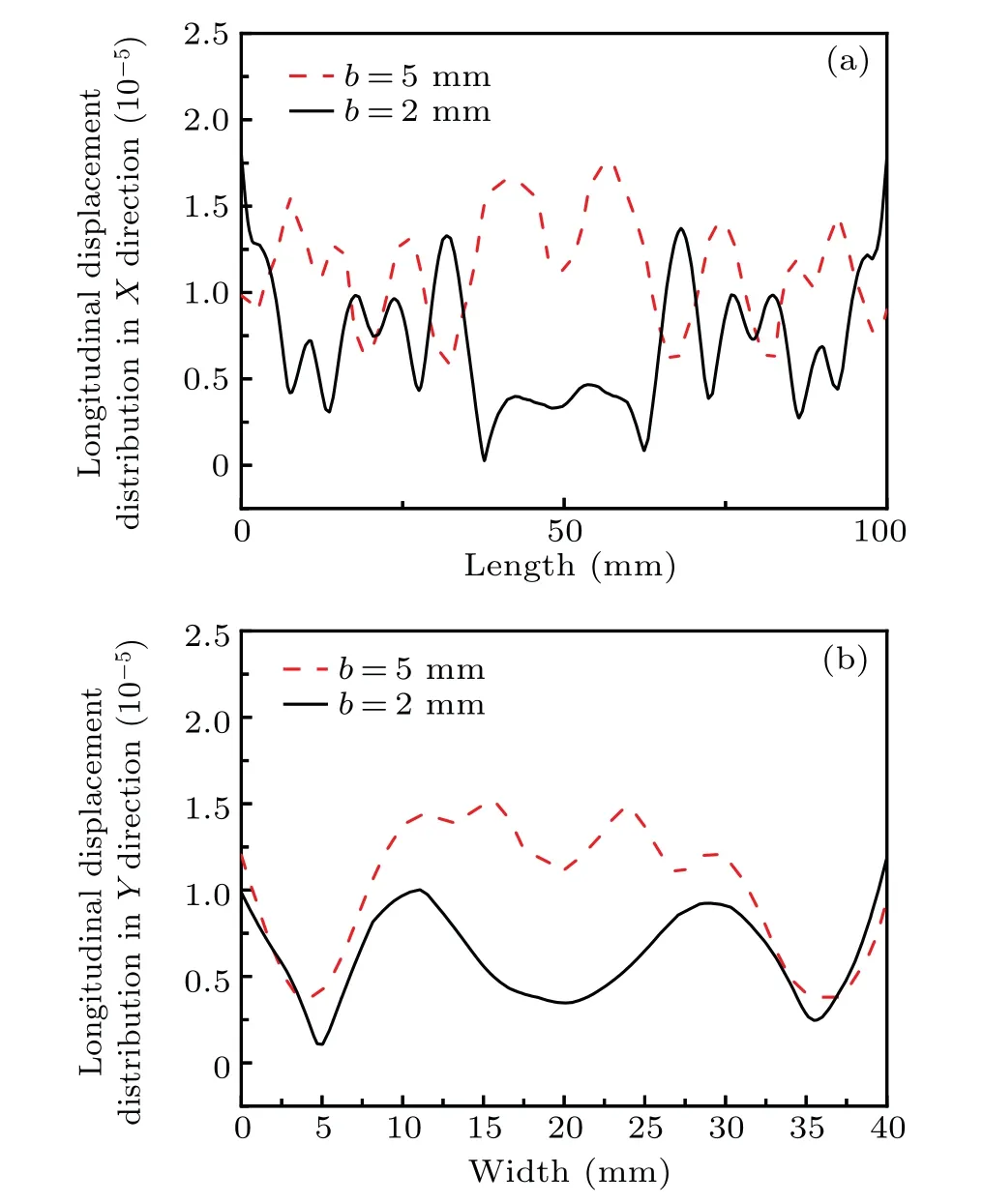
Fig. 9. Longitudinal displacement distribution of large-size rectangular piezoelectric composite plate with quasi-periodic PC structure along X (a)and Y directions(b).

4. Conclusions

In this work, a large-size rectangular composite piezoelectric plate with a quasi-periodic PC structure is presented.The equivalent material parameters of the rectangular composite piezoelectric plate are derived by using the series-parallel theory and the uniform field theory. The coupled vibration frequency equation of the piezoelectric plate is derived by introducing the electromechanical coupling coefficient, and the equivalent circuit diagram of the 3D coupled vibration is established. The vibration characteristics of the structure are analyzed by theory and finite element simulation, and the conclusions are drawn as follows.

(i)The equivalent material parameters of a large-size rectangular piezoelectric plate with a quasi-periodic PC structure are derived. By substituting the equivalent material parameters into the coupled vibration frequency equation, the resonant frequencies in theX,Y, andZdirections can be calculated.

(ii) The resonance frequency and effective electromechanical coupling coefficient can be changed by adjusting the size of the rectangular composite piezoelectric plate. The theoretical results are in good agreement with the simulation results.

(iii) The influence of material volume fraction on the thickness vibration characteristics of the large-size rectangular piezoelectric composite plate with the quasi-periodic PC structure is studied. The resonance frequency of the thickness can be located in the band gap in theXandYdirections by adjusting the volume fraction of the scatter.

(iv) When the thickness resonance frequency is within the transverse band gap range of the PC structure, the effect of the transverse vibration on the thickness vibration can be effectively suppressed. The vibration displacement distribution along the length and width of the rectangular piezoelectric composite plate are drawn when the plate vibrates along the thickness direction. The thickness vibration amplitude is increased and the vibration is more uniform by optimizing the size of the large rectangular piezoelectric composite plate with the quasi-periodic PC structure.

Acknowledgements

Project supported by the National Natural Science Foundation of China (Grant Nos. 11674206, 11874253, and 12174240)and the Fundamental Research Funds for the Central Universities,China(Grant No.020CBLY003).