Structural and thermodynamic properties of inhomogeneous fluids in rectangular corrugated nano-pores

Yanshuang Kang(康艳霜) Haijun Wang(王海军) and Zongli Sun(孙宗利)

1College of Chemistry and Environmental Science,Hebei University,Baoding 071002,China

2College of Science,Hebei Agricultural University,Baoding 071001,China

3Chemical Biology Key Laboratory of Hebei Province,Hebei University,Baoding 071002,China

4Key Laboratory of Medicinal Chemistry and Molecular Diagnosis,Ministry of Education,Hebei University,Baoding 071002,China

5Department of Mathematics and Physics,North China Electric Power University,Baoding 071003,China

Keywords: free-energy average,rectangular corrugated pore,density functional

1. Introduction

Fluids in restricted geometry have unique structures and thermodynamic properties,[1,2]which differ significantly from those of bulk phase. The confined fluids are so ubiquitous that they have obtained a wide spectrum of practical applications in technological and engineering fields, such as catalysis,[3,4]membrane separations,[5]heat exchange,[6]carbon capture and storage.[7—9]In addition, the interplay of finite size effect and surface effect in confined fluid can strongly modulate its phase behaviors,[10,11]and even rheological properties.[12—14]These distinctive properties of confined fluid make it rather fascinating and interesting.

In the past decades,confined fluid have been investigated by using of a variety of theoretical methods. Employed density functional theory (DFT), Penget al.[15]investigated the adsorption of nitrogen in MCM-41 material, which is modelled by a cylindrical pore. Sunet al.[16]studied the pressure tensor of inhomogeneous Lennard—Jones (LJ) fluids in spherical cavity. With the calculated pressure components,solid—fluid interfacial tension had also been studied. By solving the Ornstein—Zernike equation, density profiles of fluids inside slit, spherical and cylindrical pores had been studied by Zhouet al.[17—19]In addition to density profile, the partition coefficient and solvation force of the confined fluids were also investigated. In addition, computer simulations[20]are frequently employed to investigate confined fluids. By utilizing of grand ensemble Monte—Carlo (GCMC) simulation,Petersonet al.[21]studied the adsorption isotherm and phase transition of LJ fluid confined in cylindrical pore. Performing molecular dynamics (MD) simulations, Magdaet al.[22]studied density profiles, solvation forces, interfacial tensions and self-diffusion coefficients of confined LJ fluid. Despite so many investigations about the confined fluids, most of them focus on planar, spherical or cylindrical pores, because these simple geometries can be easily modelled.Nevertheless,these pores may be markedly different from real materials, whose surfaces are usually rough on an atomic scale. This has been confirmed by some recent studies on gas adsorption on some specific adsorbents.[23—25]

Prior to investigating the effect of roughness on the confined fluids, the solid—fluid potential near walls should be firstly determined. In their simulation of gases on an infinite set of straight square-walled grooves,Bojan and Steele[26](BS) obtained the solid—liquid potential by summing up the LJ pair interactions between one fluid atom and the solid.In addition, Schoenet al. had calculated the solid—fluid potential of chemically[27,28]and geometrically[29,30]heterogeneous slit pores in their investigation of the ultrathin fluid film. Following the BS method, Wuet al. derived coarsegrained potentials arising from patterned cylindrical or rectangular pillars,[31]as well as that from rectangular grooves.[32]The obtained potentials were further used in their MD simulations to probe the wetting of LJ liquid droplet on various patterned solid surfaces. Recently, Liuet al.[33]developed a general method to calculate the averaged solid—fluid potential energies for a wide range of adsorbent models with different extension and shape. By direct integration over the pair potential between the fluid and solid atoms, Malijevsk´y calculated the solid—fluid potential of solid grooved substrates.[34—38]Based on the obtained potential, a series of interfacial phenomena including filling,[34]wetting,[35]bridging,[36]interface pinning,[37]capillary contact angle, and condensation—evaporation transitions[38]had been investigated.

Though explicit results of solid—liquid potential are readily available for rough surfaces, their applications in either DFT or computer simulation may be strenuous because of the involved multi-dimension. For example, by performing a 2-dimensional nonlocal density functional theory(2D-NLDFT),Jagielloet al.[39—41]investigated the pore size distribution of adsorbents through calculation of the adsorption isotherms in rough pores. Moreover, Yatsyshinet al.[42,43]had also performed 2D-NLDFT calculations in their investigations of wetting and capillary condensation near corrugated walls. Actually, efforts have been made to simplify the DFT calculation near rough surfaces. One representative may be the quenched solid density functional theory(QSDFT),[44,45]which models the solid by the density distribution of solid atoms in the direction perpendicular to the surface rather than the source of the external potential. Besides,combining the theories of Markovian random processes and the first passage time probability,Aslyamovet al.[46,47]obtained an effective solid—fluid potential for heterogeneous surfaces, with which a random surface density functional theory(RSDFT)has been developed.

Recently,Forteet al.[48]found that the widely employed integrated potentials,such as Steele 10—4—3 potential,are only the leading-order terms in the high-temperature expansion of an original free-energy-averaged (O-FEA) solid—fluid potential. They argued that for surfaces with irregular geometrical defects, the temperature-dependent FEA potential should be more preferable. Actually, the FEA procedure provides an useful way to obtain the effective solid—fluid potentials,whose efficiency has been verified in calculations for the rough surfaces.[49]In a very recent work of Shiet al.,[50]a bottomup strategy was proposed, and the effective pore potential was calculated via a random-configuration area-weighted freeenergy-average(RC-AW-FEA)operation. This routine shows remarkable superiority over the O-FEA. However, it is not suitable for the conventional DFT calculation because of the involved random-configuration sampling. In order to extend the AW-FEA method to DFT calculations for fluid near rough surface,we aim to derive a 1-dimensional effective solid—fluid potential,with which the fluids confined in rough pore can be conveniently calculated.

This paper is organized as follow. In Section 2, a meanfield AW-FEA potential model is proposed to calculate the effective solid—fluid potential in the rectangular corrugated slit pore. In Section 3,the framework of DFT and some approximations for free energy functional of confined fluids are given.In Section 4, the structural and thermodynamic properties of confined LJ fluids in rectangular corrugated slit pores are investigated. The effects of pore geometry on these properties are analyzed in detail. In the final section,a short summary is given.

2. Mean-field AW-FEA model

The present work considers a rectangular corrugated slit pore, which is composed of two identical rectangular corrugated substrates, as sketched in Fig. 1(a). Each corrugated substrate can be regarded as the sum of a basal planar wall and an infinite set of parallel and identical pillars. These pillars are equidistantly distributed alongy-direction with a spatial periodλ=w1+w2. Note that both corrugated substrates are infinitely extended inx-andy-directions.

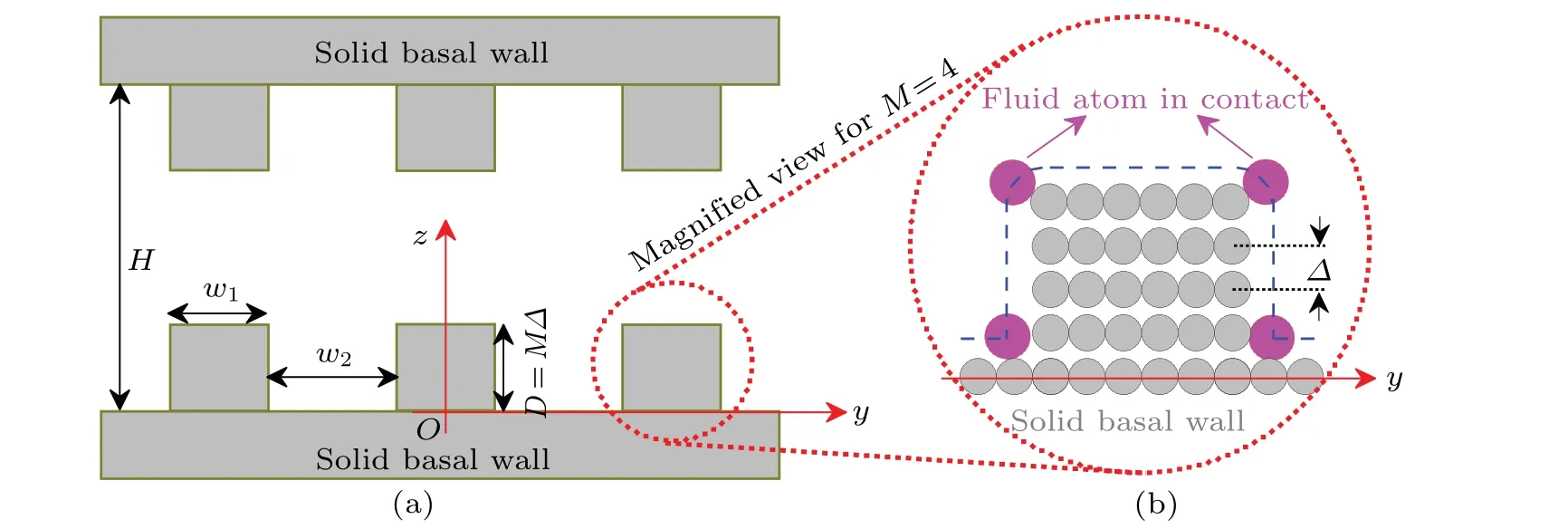
Fig. 1. (a) Cross sectional view of the rectangular corrugated slit pore. w1, w2 and D=MΔ specify the geometry of pillars. M denotes the number of layers in each pillar,while Δ is the interlayer spacing. (b)Magnified view of the pillar structure(gray)in the case of M=4. The magenta balls represent test fluid atoms in contact with the pillar,and the dashed line denotes the boundary of the accessible space around one pillar. Note that in(b),the size of balls of different species does not reflect the real size of the corresponding atom.

The solid—fluid and fluid—fluid interactions are described by the LJ potential

whereHis the separation of basal walls on the two opposite substrates, as shown in Fig. 1(a). Performing FEA calculation, one can map the 2D solid—fluid potential to an effective 1D potential,which is onlyz-dependent,that is,

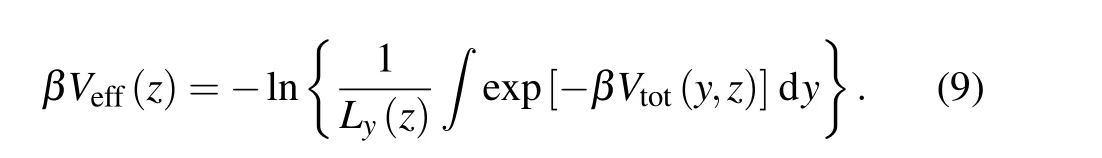
Here,β=1/kBTwithkBandTbeing the Boltzmann constant and absolute temperature,respectively. In Eq.(9),Ly(z)is the accessible length iny-direction for the fluid atom at a height ofz. The details for derivation of Eq.(9)can also be found in the supporting information. Due to the mean field treatment in the calculation ofVeff(z),the potential in Eq.(9)is referred as a MF-AW-FEA model.

In general cases, the pillars on the opposite substrates may be out of phase with each other. This may exert an effect on the 2D potential, and then on the effective potentialVeff(z). For simplicity, the present work considers only the case in which pillars on opposite substrates are symmetrical with respect to the planez=H/2.

3. Density functional theory for inhomogeneous fluids

According to statistical mechanics, the equilibrium density in inhomogeneous fluids can be determined by minimizing the grand potential functionalΩ[ρ]. For the slit pore system under consideration,it can be expressed as[52]

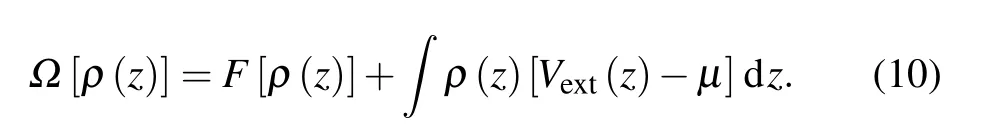
Here,F[ρ] is the Helmholtz free energy functional, whileVext(z)is the external potential,which should be replaced withVeff(z)in the MF-AW-FEA model. In addition,μdenotes the chemical potential in the bulk phase.

According to the Barker—Henderson scheme,[53]one can split the fluid—fluid interaction into repulsive and attractive parts,that is,

withΛbeing the de Broglie wavelength.

In contrast, the exact expression forFex[ρ(z)] is usually unknown for the realistic systems, and some approximation should be made for the implementation of DFT calculations. According to the perturbative split ofφff(r)in Eq.(11),Fex[ρ(z)]can be split into contributions from hard sphere and attractive tail,that is,withfatt(ρ) denoting the attractive contribution of the Helmholtz free energy per particle in bulk phase.fatt(ρ)can be obtained by combining the modified Benedict—Webb—Rubin (MBWR)[62]EoS for the LJ fluid and the Carnahan—Starling (CS)[63]EoS for the hard sphere fluid. More details about the WDA calculation can be found in our previous works.[64,65]

OnceFex[ρ(z)] is constructed, the equilibrium density can be calculated by minimizing the grand potentialΩ[ρ(z)],which leads to the Euler—Lagrange equation

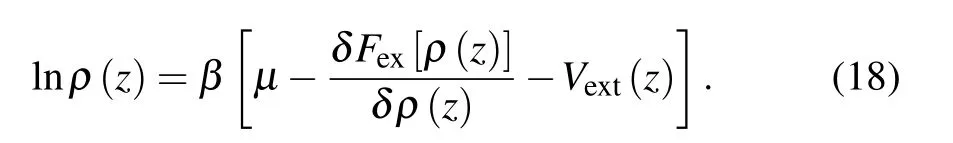
Prior to the calculation ofρ(z),Vext(z) should be calculated firstly by Eq.(9).Actually,determination ofVext(z)is straightforward because analytical expression for the 2D fluid—solid potential has been obtained in Eqs. (4)—(8). For an obtainedVext(z), the nonlinear equation, say Eq. (18), is solved in a standard manner by Picard iteration method with the grid size of 0.02σ. The iterations are continued until the sum over the grid points of the absolute values of the differences between two consecutive iterations is smaller than 10-6. In the calculation, the involved numerical integrations and convolutions are all determined by the standard trapezoidal quadrature. More detail about the algorithm of DFT calculation can refer to Ref.[56]and the references in it.

Unlike the case of smooth pore, the involved spatial integration∫∫dxdyin calculations for rough pores is no longer a constant. Instead, it should bez-dependent because the pillars prohibit the fluid particles from entering the region they have occupied, as sketched in Fig. 1(b). Therefore, any volume integral of the form∫∫(·)dxdydzshould be replaced by∫(·)Aacc(z)dz. Here,thez-dependent accessible areaAacc(z)can be obtained as follows:

withρbthe fluid density in the bulk phase.

4. Results and discussion

In DFT calculations for inhomogeneous fluid,the external potentialVext(z)plays a decisive role because it makes the confined fluid different from the corresponding bulk phase.To understand the potential arising from the rectangular corrugated slit pore, we have calculated the 2D wall potentialVtot(y,z).A contour ofVtot(y,z) for argon atom between two adjacent pillars withw1/σ=w2/σ=D/σ=3.0 has been presented in Fig. 2. It is obvious that for the given geometry of substrate, the potentialVtot(y,z) has a specific distribution near the substrate. It is quite different from that of the smooth pore,because the pillars on the substrate make the potential inhomogeneous alongy-direction.

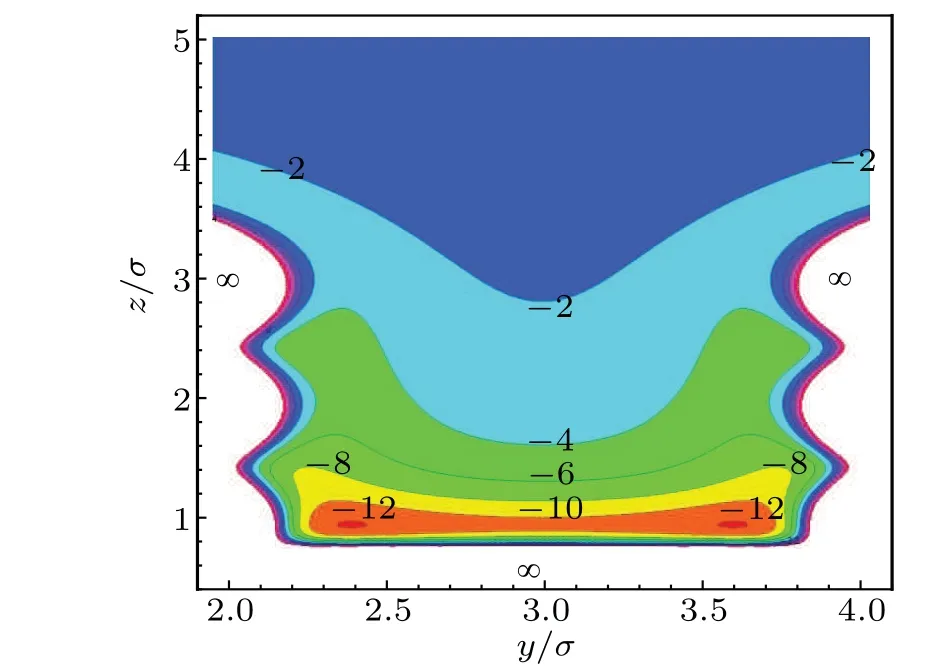
Fig.2. Contour of the 2D wall potential βVtot(y,z)of argon atom between two adjacent pillars. The reduced parameters are set as w1/σ =w2/σ =D/σ =3.0,σss/σ =1.0,εss/ε =1.0 and ρsσ3=1.0.

In order to apply the MF-AW-FEA model to the DFT calculations, we have calculated the 1D effective solid—fluid potential in the rectangular corrugated slit pores with different geometry. The results for argon at 87.3 K are shown in Figs. 3(a)—3(c). For the purpose of comparison with the results from RC-AW-FEA model,[50]which has simulated the potential from one single rough wall, the pore width in our calculation has been set asH/σ=20.0. This pore width is large enough to regard that the two corrugated substrates are immune to each other. In addition, other parameters in the MF-AW-FEA calculations are set the same as those used in the simulation,which has been listed in Table 1.

Table 1. Parameters used for calculation of Vext(z) with the MF-AW-FEA model; in Figs.3 and 4(c)for argon at 87.3 K,while in Figs.7 for CO2 at 273 K.

Figure 3(a) presents the 1D effective external potential near a rectangular corrugated substrate withw1/σ=w2/σ=3.0 andD/σ=1.0—4.0. Obviously, the potential from MFAW-FEA shows a similar pattern to that of potential from RCAW-FEA.[50]Specifically,each curve has two minima,one atz1≈σ,while the other atz2≈D+σ. Actually,the minimum atz2arises from the attraction of top surface of the pillars. In the case ofD/σ=1,the result from MF-AW-FEA is slightly higher than that from RC-AW-FEA. This stems from the different manner in which the roughness of substrate is modeled.That is,the substrate is defined to be rectangular corrugated in the MF-AW-FEA model, while it is random sampled in RCAW-FEA model. Furthermore, it is shown that for a largerD,the potential curve is generally lowered in between the two minima.This can be attributed to the enlarged lateral area generated by higher pillars, which provide more adsorptive sites on the microscopic point of view.

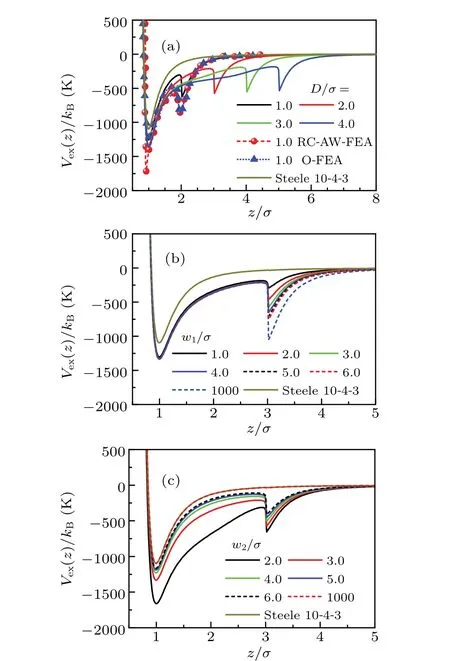
Fig.3. MF-AW-FEA model of the potential for argon atom in the rectangular corrugated pores of different parameters,but all with H/σ=20.(a) Effect of D on Vext(z). Lines are results from MF-AW-FEA with w1/σ =w2/σ =3.0,while lines with symbol are those from RC-AWFEA and O-FEA by MC simulation.[50] (b) Effect of w1 on Vext(z),with w2/σ =3.0 and D/σ =2.0. (c) Effect of w2 on Vext(z), with w1/σ =3.0 and D/σ =2.0.

Effect ofw1on the 1D effective external potential is depicted in Fig.3(b). Obviously,the two minima on each curve coincide at the same position because the height of the pillars has been fixed. Further comparison suggests that the potential is lowered with the increase ofw1,especially in the region near the top of the pillars. Actually, largerw1corresponds to wider top area of the pillars. By averaging alongy-direction,this leads to stronger attraction there. Further,the effect ofw2on the 1D effective external potential is presented in Fig.3(c).It is obvious that the effect ofw2on the potential is just opposite to that ofw1. For the case ofw2/σ=1000,the potential curve coincides completely with that of Steele 10—4—3 potential, which indicates the vanishing influence of the pillars in this limiting case.

Having obtained the effective 1D potential for the rectangular corrugated pores,one can proceed with calculations for the structure and thermodynamic properties of fluid in these pores. However, it is necessary to check the performance of our DFT calculation at first. To this end,we perform calculation for confined LJ fluid in a smooth slit pore,which is modelled by Steele 10—4—3 potential. The results in Fig.4(a)suggest a good agreement between DFT results and those from MC simulations.[66]

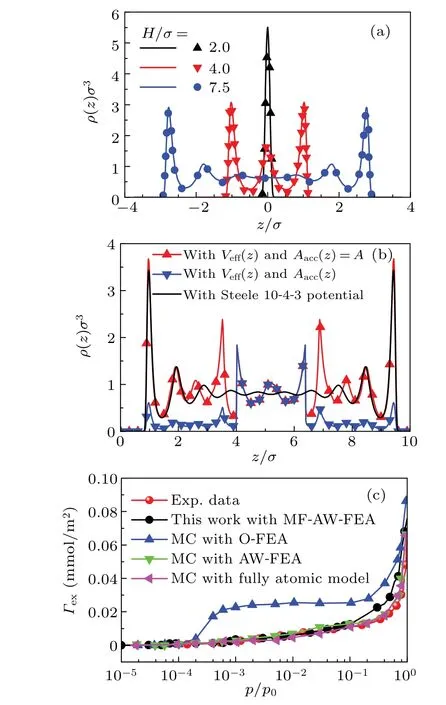
Fig.4.(a)Density profiles of LJ fluid confined in smooth slit pores with kBT/ε=1.2 and ρbσ3=0.5925.Lines are results from our DFT calculations,while symbols are results from MC simulations.[66](b)Density profile of argon fluid confined in a smooth pore and rectangular corrugated pore with w1/σ =w2/σ =D/σ =3.0. In both calculations,we set ρbσ3 =0.8, kBT/ε =1.2 and H/σ =10.4. (c) Excess adsorption isotherms of argon at 87.3 K on the BP-280 solid by different models of pore potential. For the purpose of comparison,experimental data[67]and GCMC results[50] are also included.

Example sets of density profile for fluid in rectangular corrugated slit pores are shown in Fig. 4(b). In the calculation, parameters are set asw1/σ=w2/σ=D/σ= 3.0,H/σ=10.4,kBT/ε=1.2,andρbσ3=0.8. As stated above,fluid particles cannot enter the region that the pillars have occupied. Therefore,the accessible region should be considered,and the density output by the DFT calculation should multiply the qualityAacc(z)/A. As shown in Fig. 4(b),both density curves, with and without the consideration ofAacc(z), show maximum atz=4σ, which implies the minimum ofVeff(z)there. In contrast,both curves coincide between 4σand 6.4σbecauseAacc(z)/A=1 in this region. Furthermore,comparison ofρ(z)between smooth and corrugated pores shows that they are markedly different, especially in the region near the top surface of the pillars.This indicates that the pillars can significantly modulate the fluid structure in the corrugated pore.

In order for a further verification of the efficiency of the MF-AW-FEA model, calculation for the excess adsorption isotherms of argon on BP-280 solid is performed atT=87.3 K.The result withw1/σ=7,w2/σ=3.0 andD/σ=1.0 is given in Fig. 4(c). In the figure, results from experimental measurement[67]and GCMC simulation[50]are also presented for a purpose of comparison. In the calculation, the pore width is set asH/σ= 20.0. Evidently, the DFT result agrees very well with the experimental data in the regionp/p0∈(10-5,0.1). With a further increase ofp, the curve shows a modest deviation from the data. The deviation can be ascribed to the mean-field treatment in the MF-AW-FEA model. Even so,the DFT result with MF-AW-FEA model still shows better agreement with experimental data than GCMC results with O-FEA model,in the region ofp/p0∈(10-4,1).

10月19日早上8：20，离金樽奖论坛开幕还有40分钟时，我见到了David。他背着鼓囊囊的挎包，一步步走向舞台，一边的肩膀被压得微微有些倾斜。坐了一个晚上的飞机，早上6点才落地广州，他看起来似乎有些疲惫。论坛、大师班、品鉴会、晚宴，4场几乎无缝衔接的活动都需要他在场发言或是主持，这天对David而言会是漫长的一天。

4.1. Excess adsorption isotherms

Excess adsorption is important in either theoretical or engineering analysis, and may provide noteworthy information about the global behavior of confined fluids.To understand the effect of pore geometry on excess adsorptionΓex, adsorption isotherms of confined LJ fluids in the rectangular corrugated slit pores are calculated in different cases ofH,D,w1,andw2.The results are given in Figs. 5 and 6. In Fig. 5, dependence ofΓexonHfor LJ fluid confined in smooth slit pores is firstly calculated withkBT/ε=1.2 andρbσ3=0.5925.Comparison with MC results[68]shows that they agree well.

In Figs.5, results for excess adsorption withw1/σ=1—6 show that for each value ofw1,Γexpresents oscillatory increase withH.This can be understood as follows.For the pore width that gives a maximum ofΓex, the fluid configuration in the pore is more ordered, which indicates that the particles are efficiently arranged in layer structures, and the available space is utilized in a better way. In addition,the period of oscillation is nearly one diameter, which displays the influence of hard sphere excluded volume on determining the packing of the confined fluid. Further comparison between the curves shows that the oscillation ofΓexand its amplitude are enhanced by largerw1,which indicates the constructive influence ofw1onΓex.

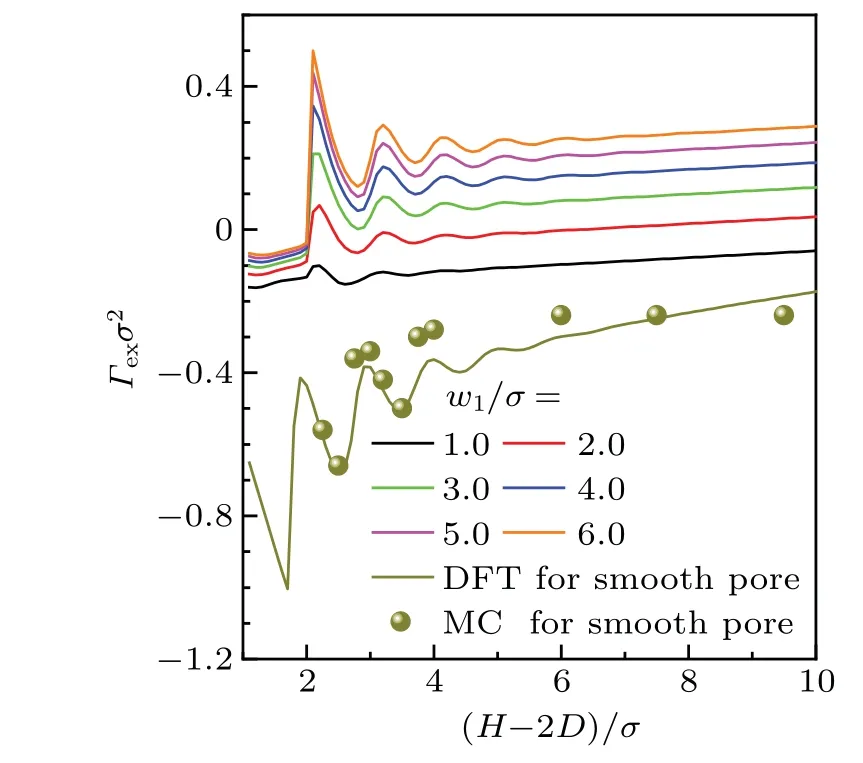
Fig. 5. Dependence of Γex on H for confined LJ fluids in the rectangular corrugated pores with different w1. Other parameters are set as kBT/ε =1.2,ρbσ3=0.5925,w2/σ =3.0 and D/σ =2.0. In calculation for smooth pore, we set kBT/ε =1.2 and ρbσ3 =0.5925, which are the same as those used in MC simulations.[68]

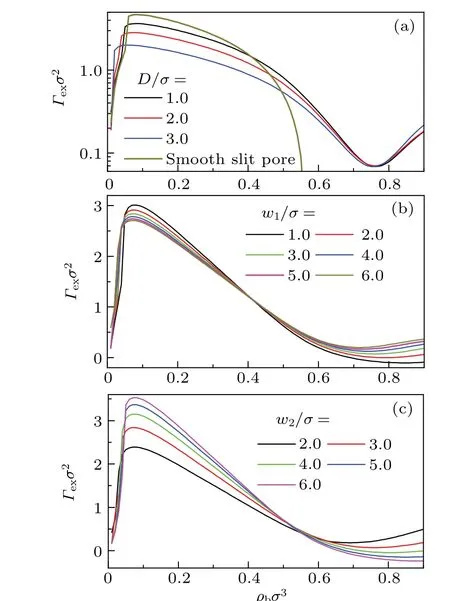
Fig. 6. Excess adsorption isotherms of confined LJ fluids in different rectangular corrugated slit pores. kBT/ε =1.2 and H/σ =10.0 has been set in the calculations. Specifically, (a) dependence of isotherms on D with w1/σ =w2/σ =3.0. (b) dependence of isotherms on w1 with w2/σ =3.0 and D/σ =2.0. (c) dependence of isotherms on w2 with w1/σ =3.0 and D/σ =2.0. In (a), logarithmic axis is used to show its variation in the high density region.

It is evident in Fig. 6(a)that in the low and high density regions,the height of pillar exerts an opposite influence onΓex.Actually,there is a competitive mechanism about the effect ofDonΓex.For a largerD,the higher pillar leads to an adsorptive effect because it provides more adsorptive sites. On the other hand, largerDleads to wider depletion layer around the pillar. This depletion region prohibits the particle from entering,and then depresses the adsorption. The winner in the competition depends on the density in the pore. For sufficiently large densities, multi-layer structures occur in the pore, and then the former is dominant. In contrast,for low densities,the latter holds an advantage, because the increase ofΓexarising from additional adsorptive sites is not enough to compensate the decrease ofΓexarising from the enlargement of the depletion layer.

Results in Fig. 6(b) suggest thatw1has the same effect onΓexasD. With the increase ofw1, the adsorptive effect and depletion effect win their competition in high density and low density region,respectively. However,the switching point has been shifted leftwards. This implies that the advantage of depletion effect has been depressed in its competition with the adsorptive effect,because the depletion layer keeps unchanged asw1varies. In contrast,Fig.6(c)shows that the effect ofw2onΓexis opposite to that ofw1. With the increase ofw2, the adsorptive effect of the pillars is weakened,because its attraction has been lowered by the area-weighted average in a larger spatial region.

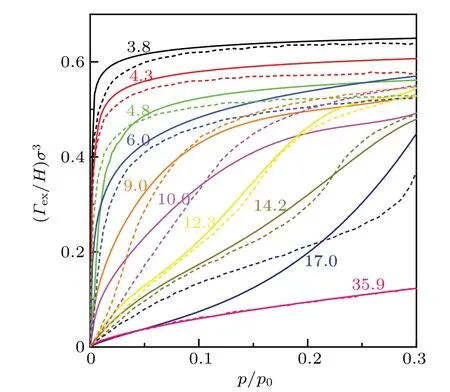
Fig. 7. Excess density of CO2 confined in sinusoidal corrugated slit pore with different widths. The solid and dashed lines are results of this work and 2D-NLDFT[69] calculation,respectively. Note that lines with the same color correspond to results for the identical pore width. The number in the figure denote the pore width,but in units of °A.

It is necessary to point out that the procedure proposed here should not be limited to this specific roughness, but should be applicable for other complex, or even random surface, so long as its shape or geometry can be mathematically described. As a test, we perform calculations for confined CO2in a sinusoidal corrugated slit pore, which has been investigated with 2D-NLDFT by Jagielloet al.[69]Based on the 2D wall potential proposed by Jagielloet al., an effective 1D wall potential can be calculated by using the MF-AWFEA model. The parameters in the calculation has been given in Table 1. The excess densities of confined CO2at 273 K are shown in Fig. 7. The comparison with results from 2DNLDFT suggests that they agree well for all the chosen pore widths. This demonstrates the good performance of the MFAW-FEA model in its application to other rough pores.

4.2. Solvation force

In smooth slit pore, solvation force is the normal force exerted by the fluid on per unit area of each wall. Its oscillating behavior has been confirmed in smooth pores. However,solvation force between some non-crystalline surfaces may be different due to their molecularly roughness on the surfaces.To understand the effect of roughness on solvation force,calculations are performed for the LJ fluid confined in the rectangular corrugated slit pore. In the context of thermodynamics,the solvation force can be expressed as[70]

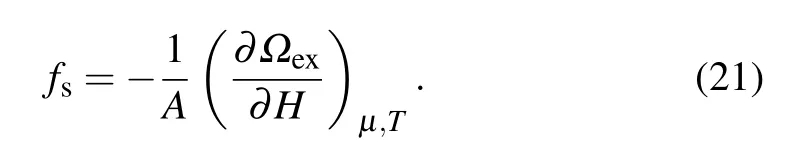
Here, excess grand potentialΩex=Ω+pVwithpthe bulk pressure, andArefers to the projected area of the substrates.Note that the effect of pillars onfshas been taken into account in the calculation ofΩex.

Firstly, the dependence offsonHis calculated for the confined LJ fluid in rectangular corrugated slit pores. The results in Fig.8 show that for each case ofD,fsexhibits oscillating behavior withH. Moreover,the period of oscillation is nearly one diameter of the fluid particle. For the same reason as that for the oscillation ofΓexin Fig.5,the oscillation offsstems from the variation of the ordered configuration of fluids in the pore. Obviously, each curve exhibits a maximum near(H-2D)/σ=2.0. This maximum corresponds to an ordered layer structure in the fluid,while the subsequent maxima in the curve indicate the newly formed layers in the pore.In addition,the solvation force is generally negative for the pore satisfies(H-2D)/σ ＜2.0, which indicates an attraction between the opposite walls.

It is apparent in Fig.8 that the oscillation amplitude offsfor the rectangular corrugated pore is much smaller than that for the smooth slit pore.Moreover,the oscillation amplitude offsis weakened asDis increased. AsDis large enough,its influence onfsmay be too small to be distinguished.This can be ascribed to the higher pillars,which destroy the ordered layer structure,and then weaken the normal pressure and solvation force in the pore. Actually, in order to quantify the effect of geometrical roughness on solvation force, Frinket al.[71]had proposed an empirical fitting with an exponentially decaying oscillatory function. According to their fitting,the oscillation amplitude of the solvation force decreases significantly with the roughness, though a weak increase occurs as the roughness is further increased. Obviously,this is consistent with the results in Fig.8.

In order for a better understanding of the effect of roughness onfs,the dependences offsonw1andw2are also calculated. The results are given in Fig.9. Results in Fig.9(a)show that for the given value ofHand other chosen parameters,fsincreases monotonously withw1,while its rate of increase decreases withH.WhenHis large enough,fsmay become independent onw1,just as shown in the case ofH/σ=12.0.While in Fig. 9(b),w2shows an opposite effect onfs. This can be understood by the superposition approximation,[71,72]which interprets the solvation force in rough pore as a weighted average of those in several smooth pores of different width. For the rectangular corrugated slit pore under consideration,it involves only two types of smooth slit pore of widthsHandH-D. For the givenHandD, increasing ofw1leads to a larger weight of the smooth pore of widthH-D. This causes an enhancement offs,becausefsin narrower pores is stronger than that in wider pores.On the contrary,increasing ofw2corresponds to a larger weight of the wider smooth pore of widthH, which interprets the reason whyfsdecreases withw2, as shown in Fig.9(b).

Fig. 8. Dependence of fs on H under different conditions of D.w1/σ =w2/σ =3.0, ρbσ3 =0.8 and kBT/ε =1.2 are set in the calculations. For the purpose of comparison,the corresponding results for smooth pore is given by the dark yellow line. Note that except the curve for D/σ =1.0, other curves have been shifted up by 1 in turn from bottom to top.

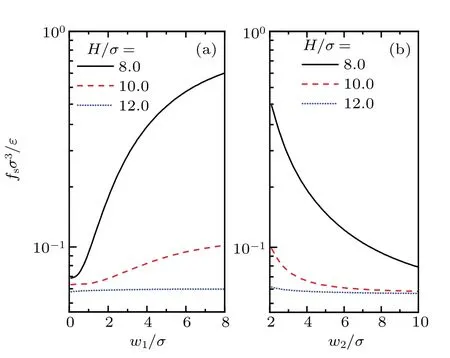
Fig.9. Effects of w1 and w2 on fs for confined LJ fluids with ρbσ3 =0.8, kBT/ε =1.2 and D/σ =2.0. For(a), w2/σ =3.0, while for(b),w1/σ =3.0.

4.3. Absolute and relative surface free energies

For fluid near smooth substrate or in pores, surface tension can be well defined in formal thermodynamics. However,surface tension in rough pores gets more complicated because the complex geometry may result in inhomogeneity and anisotropy of the surface tension.[73]Besides,the rough geometry and the anisotropy of surface tension make it a difficult task to determine the surface of“tension”,because it depends heavily on the geometrical characteristics of the rough substrate. In contrast, calculation of surface free energy is more convenient,since it is a global measurement of the whole system.

According to the formal statistical mechanics, surface free energy in a slit pore can be calculated as the excess grand potential per unit area over that of bulk phase[74]

whereΩex(H)stands for the excess grand potential in the pore of a widthH,whileΩex(∞)represents that in the limit case ofH→∞. Physically, Eq. (22) defines an absolute surface free energy,while Δωsin Eq.(23)is a relative measurement of the surface energy for fluid in pore with finiteHover that in a reference pore. Therefore, the minimum of Δωsmay supply information about the equilibrium separation the two substrates.

In order to obtain useful insight to understand interfacial phenomena near rough substrates,bothωsand Δωsfor LJ fluids confined in a rectangular corrugated slit pore have been calculated withρbσ3=0.8 andkBT/ε=1.2. Effects ofH,w1andw2are given in Fig.10. In Figs.10(a)and 10(d),comparison between results ofωsand Δωsin different cases ofDsuggests thatωs,Δωs,and their oscillating amplitudes withHare all depressed with the increasingD.The pillars on the substrate should be responsible for the depression because higher pillars may destroy the ordered layer structure of fluid in the pore.

Further,Fig.10(a)shows that for each value ofH,ωsbecomes more negative asDincreases. In the Young’s scheme,it corresponds to smaller contact angle and enhanced hydrophilicity of the wall.[75]This results from the expanded lateral surface and more adsorptive sites on it. Further, asHis increased, eachωscurve decreases to an asymptotic value,which corresponds to the isolated substrate case.In Fig.10(b),ωsdecreases monotonously withw1for each value ofH. This can be ascribed to the enhanced confinement effect that arising from the narrow space between the top surface of pillars on the opposite substrates. For the obvious reason,effect ofw2onωsis just opposite to that ofw1,as shown in Fig.10(c).

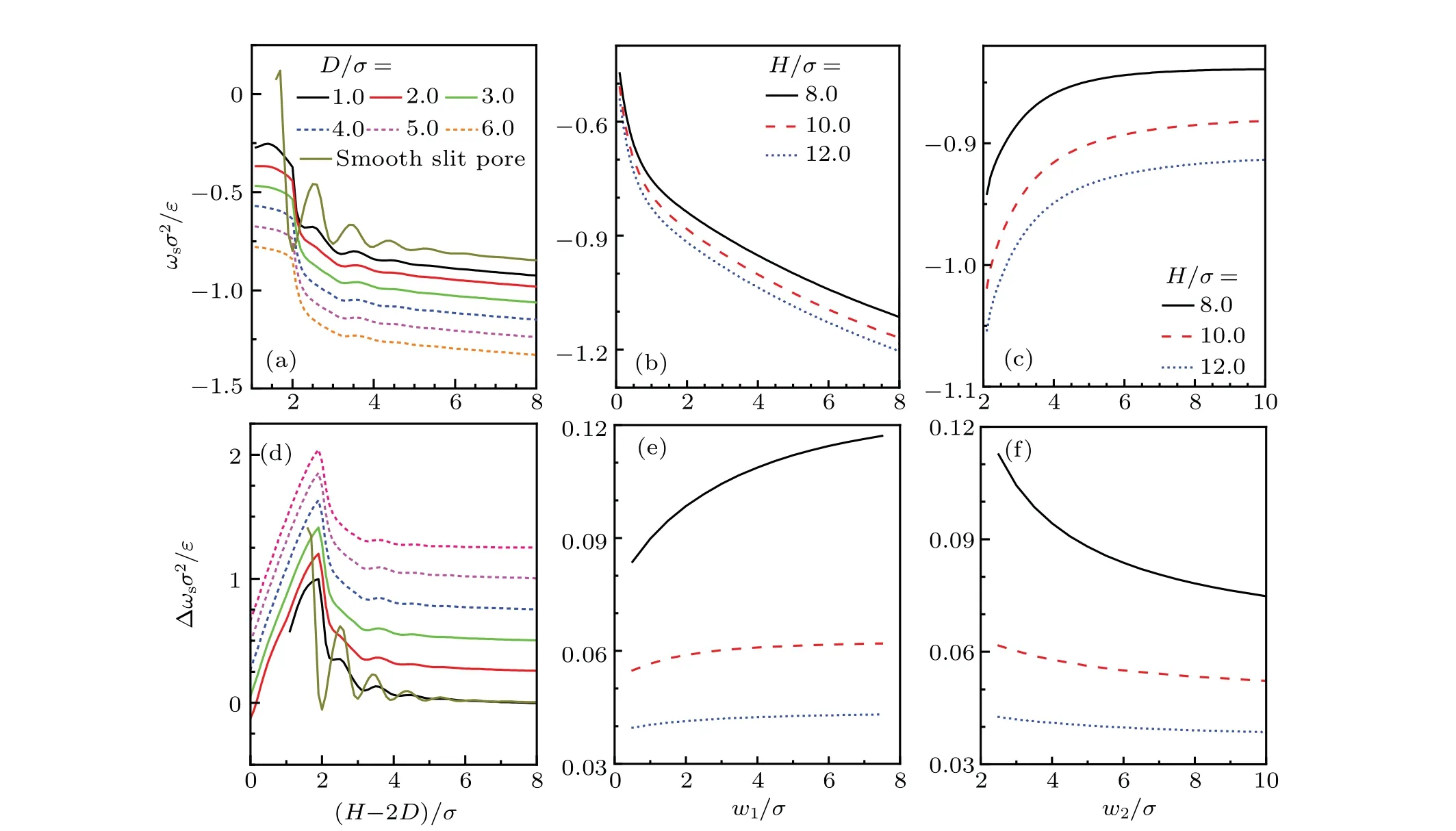
Fig.10. The ωs and Δωs of confined LJ fluids with ρbσ3=0.8 and kBT/ε =1.2. (a)—(c)Dependence of ωs on H,w1 and w2 under different conditions. (d)—(f)Dependence of Δωs on H,w1 and w2 under different conditions. Specifically,in(a)and(d),w1/σ =w2/σ =3.0. In(b)and(e),w2/σ =3.0,D/σ =2.0. In(c)and(f),w1/σ =3.0,D/σ =2.0. The curves in(d)have been shifted up by 0.25 in turn from bottom to top,except that for D/σ =1.0.

Results for Δωsare given in Figs.10(d)—10(f).Obviously,Δωsexhibits extremely weak dependence onD,and it tends to zero whenHis sufficiently large. As also shown in Figs.10(e)and 10(f),w1andw2modulate Δωsin an opposite manner,while they exert an extremely weak influence on ΔωsasHis large enough. Unlikeωsin Fig. 10(b), Δωsin Fig. 10(e)monotonously increases withw1for each case ofH. This means that wider pillars enhance the correlation between the opposite corrugated substrates, and then leads to larger Δωs,as suggested by the superposition approximation.[71]

4.4. Thermodynamic response functions

Thermodynamic response functions, which are defined as the first derivative of fundamental thermodynamics qualities,provide rich information about critical behavior and phase transition. However, there are too many such derivatives and relations between them. Actually, Bridgman[76]had picked out three fundamental members, and all other response functions can be expressed in terms of the three. These three functions are isobaric thermal expansivityαP,isothermal compressibilityκTand isobaric heat capacityCP(inNPTensemble). Note that for canonical ensemble,CPshould be replaced by isochoric heat capacityCV,which relatesCPvia the relationCP=CV+TVα2Pκ-1T.[77]Here,Vis the volume of the fluid.

By utilizing the fundamental thermodynamic relation,the above thermodynamic response functions are usually calculated as[77]

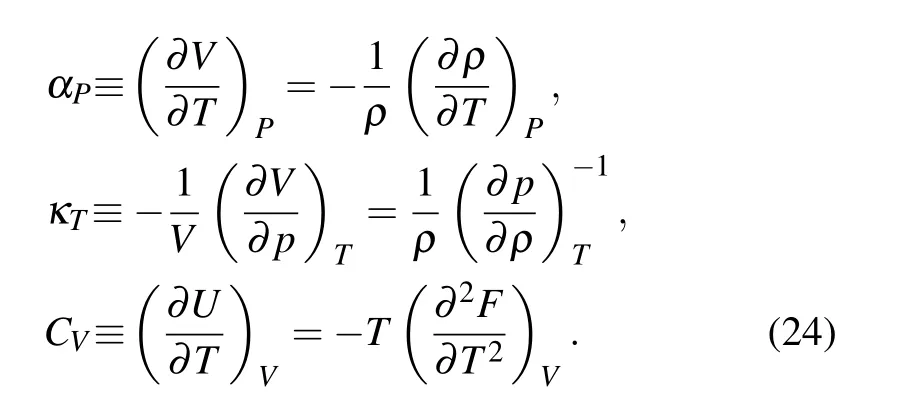
Actually,these scalar equations are originally defined for uniform bulk phase. However, in confined fluids, some of these properties may be position-dependent or even tensors. Takes the isothermal compressibilityκTin confined fluid for example, one should calculate its components by using the corresponding components of pressure tensor. However, in an ultrasonic experiment forκTin confined fluid, its anisotropy cannot be measured experimentally. Therefore, one usually regardsκTas a scalar or an averaged macroscopic value,with which the confined fluid is regarded as a whole. This is likely to represent the experimental observable in ultrasonic experiment. Similarly, in the calculation of the thermodynamic response functions,one can also regard them as averaged macroscopic quantities, though they maybe position-dependent on the atomistic level.

Fig. 11. Dependence of αP, κT and CV on H, w1 and w2 for confined LJ fluids with ρbσ3 =0.8 and kBT/ε =1.2. The top, middle and bottom rows are results for αP,κT and CV,respectively. The left,middle and right columns show respectively the H,w1 and w2 dependence of thermodynamic response functions. The same type of lines in each column correspond to the same value of parameters in calculations.Specifically,(a)—(c)w1/σ =w2/σ =3.0,(d)—(f)w2/σ =3.0 and D/σ =2.0,(g)—(i)w1/σ =3.0 and D/σ =2.0.

Figures 11(a), 11(d) and 11(g) present results forαPof confined LJ fluids in rectangular corrugated slit pores. Figure 11(a) shows thatαPdescends oscillatorily withH. The oscillatory behavior results again from the ordered configuration of the fluid in the pore, while its decline can be understood by the increase ofρavwithH, which has been shown in Fig.5. In a denser fluid,the stronger excluded volume depresses its expansion with temperature, and then leads to a smallerαP. In addition, decreasing ofαPwithDstems from the enlargement of lateral area around the pillars, which may adsorb more particles and then depressesαP. Influences ofw1andw2onαPare given in Figs.11(d)and 11(g),respectively.As shown in Fig.6(b),ρavincreases withw1for the bulk densityρbσ3=0.8. Therefore, asw1increases,αPshould be depressed by the enhanced excluded volume in the fluid. The influence ofw2onαPis just on the opposite.

Results ofκTfor LJ fluid in rectangular corrugated slit pore are given in Figs.11(b),11(e)and 11(h). Obviously,influences ofH,D,w1andw2onκThave the same patterns as those onαP.This is owing to the fact that fluid is more difficult to deform for a larger average density. In contrast,influences ofH,D,w1andw2onCVof LJ fluid in corrugated slit pore is just opposite to those onαPandκT. This is because in a fluid with larger average density,stronger correlation between particles results in an increase of inter energy,and then its isobaric heat capacityCV. This is consistent with the results presented in Figs.11(c),11(f)and 11(i).

5. Conclusion

In conclusion, structural and thermodynamic properties of confined LJ in rectangular corrugated slit pores are investigated by classical density functional theory. At first,a method for effective 1D solid—fluid potential, say the MF-AW-FEA model, is proposed for the rectangular corrugated slit pore.Application of this effective 1D potential to the adsorption of argon on BP-280 has verified its ability and effectiveness in the investigation of fluids near rough surface. Further,the effective 1D potential has been employed to calculate the structure of LJ fluids confined in rectangular corrugated slit pore of different geometrical characteristics. Based on the obtained density in the corrugated pore, the thermodynamic properties including excess adsorption isotherms,solvation force,surface free energy, and thermodynamic response functions of fluids,are calculated respectively. The influences of pore geometry on these properties are investigated.

The results suggest that the geometrical parameters includingH,w1,w2andDof the rectangular corrugated slit pore, have distinct influences on these properties. Firstly, the increase ofw1orDcan enhance these properties, whilew2shows an opposite effect. Secondly, these properties usually exhibit oscillation with pore width due to the variation of the ordered configuration of fluid in the pore. The amplitude of the oscillation can also be modulated by the geometrical characteristics of the pore. Thirdly,in the limiting case ofw1→∞orw2→∞, the corrugated pore approaches to a smooth pore of specific width,and these thermodynamic properties tend to those of the corresponding smooth pore. In summary, these results provide us some novel and interesting insight about the fluids confined in rough pores. It is expected to be helpful to explore relevant issues including wetting,bubble,droplet and other interfacial phenomena near surfaces of complex topology.

Acknowledgements

Project supported by the National Natural Science Foundation of China (Grant No. 21503077), the Fundamental Research Fund for the Central Universities of China (Grant No.2020MS147),and the Science and Technology Project of Hebei Education Department,China(Grant No.QN2018119).