Topological Lifshitz transition and novel edge states induced by non-Abelian SU(2)gauge field on bilayer honeycomb lattice

Wen-Xiang Guo(郭文祥) and Wu-Ming Liu(刘伍明)

1Beijing National Laboratory for Condensed Matter Physics,Institute of Physics,Chinese Academy of Sciences,Beijing 100190,China

2School of Physical Sciences,University of Chinese Academy of Sciences,Beijing 100190,China

3Songshan Lake Materials Laboratory,Dongguan 523808,China

Keywords: topological Lifshitz transition,SU(2)gauge field,bilayer honeycomb lattice

1. Introduction

In recent decades,the discovery of topological insulators has extended our understanding of topological states of matter tremendously.[1–3]In Landau theory of phase transitions,different states of matter are classified by spontaneous symmetry breaking. However, topological states cannot be distinguished from topological trivial states by symmetry, and thus topological phase transitions can not be characterized by a local order parameter.[1–3]Consequently, various topological invariants are introduced to identify the topological phase transitions.[1–3]Different from usual topological transitions,topological Lifshitz transitions[4–6]are determined by topologies of Fermi surfaces in momentum space. They are accompanied by the change of topology of Dirac points,[7]Weyl points,[8,9]nodal lines,[10,11]and so on.[5]

Since the first preparation of graphene,[12]twodimensional materials have been investigated widely due to their various exotic properties and prospective applications. For instance, the charge carriers in graphene are massless Dirac fermions described by Dirac’s relativistic equation,[13–15]which allows for the investigation of quantum electrodynamic phenomena. Furthermore, the Fermi surface of several Dirac points also makes graphene an excellent platform to study topological Lifshitz transitions.[4,5]However,owing to the inevitable disorder,defects,and impurities in materials,it is difficult for us to manipulate the materials arbitrarily. Fortunately, ultra-cold atoms in optical lattices[16,17]provide a flexible and controllable playground to stimulate the phenomena in condensed matter and particle physics, such as Mott transition[18–20]and gauge invariance.[21]Artificial gauge fields on neutral atoms have been created by atom–laser interaction,[22–27]which makes it possible to investigate the topological phase transitions in optical lattices.[28–42]

The SU(2) gauge effects on the honeycomb lattice have been investigated thoroughly.[30,31]The non-Abelian gauge potential induces an annihilation and creation of massless Dirac points. Different from the massless Dirac fermions in graphene,the charge carriers of bilayer graphene are massive chiral quasiparticles.[43,44]What’s more, a tunable band gap has been realized by applying a biased electric field on bilayer graphene.[45–49]Accordingly,bilayer honeycomb lattice(BHL)has been studied widely and various exotic phenomena have been discovered.[50–59]Thus how the SU(2) gauge field will act on the BHL deserves to be investigated.

In this work, we investigate the SU(2) gauge effects on BHL.Based on the tight-binding model,we obtain the model with SU(2) gauge potential by Peierls substitution.[30,60,61]Then we discover a topological Lifshitz transition induced by the non-Abelian gauge potential by calculating the Fermi surfaces. The phase diagram of the gauge fluxes is also obtained by solving the secular equation. In addition,edge states of biased bilayer ribbons are studied under the influence of gauge potential.

The paper is organized as follows. In Section 2, we introduce the model. Then we analyze the topological Lifshitz transition induced by the non-Abelian SU(2) gauge potential in Section 3 and obtain the phase diagram of the transition in Section 4. Next in Section 5,the edge states of biased bilayer ribbon with gauge fluxes are studied. Finally, we summarize our results briefly in Section 6.

2. Tight-binding model with SU(2)gauge potential

Fig. 1. (a) The illustration of the AB-Bernal stacking bilayer honeycomb lattice(BHL).(b)Top view of the BHL lattice. The cell consists of four sites,including A1(B1)in the lower layer and A2(B2)in the upper layer. The lattice primitive vectors a1 =(,-),a2 =(,).(c)The frist Brillouin zone(FBZ)and the reciprocal lattice vector b1= (1,-, b2 = (1,. K = 23π (1,) and K′ = (1,-)are two inequivalent corners of the FBZ.(d)The energy band structure for the Hamiltonian(2)along the loop Γ →K →M →Γ in the FBZ.One conduction band and one valence band touch parabolically at the K point no matter what t⊥equals to.

The AB-Bernal stacking BHL,as shown in Figs.1(a)and 1(b), is commonly described by a tight-binding Hamiltonian with the nearest-neighbor intra-layer hopping and the interlayer hopping betweenA1andA2sites,[13–15,62–65]which is symmetric around the zero energy due to the electron–hole symmetry. We also find thatf(k) = 0 for two inequivalent corners of the first Brillouin zone (FBZ)[Fig.1(c)],such that the lower conduction band and upper valence band touch at zero energy at the cornersKandK′. We definek=K+qnear theKpoint and expand the spectrum to investigate the low-energy properties. The low-energy band spectrum is approximately

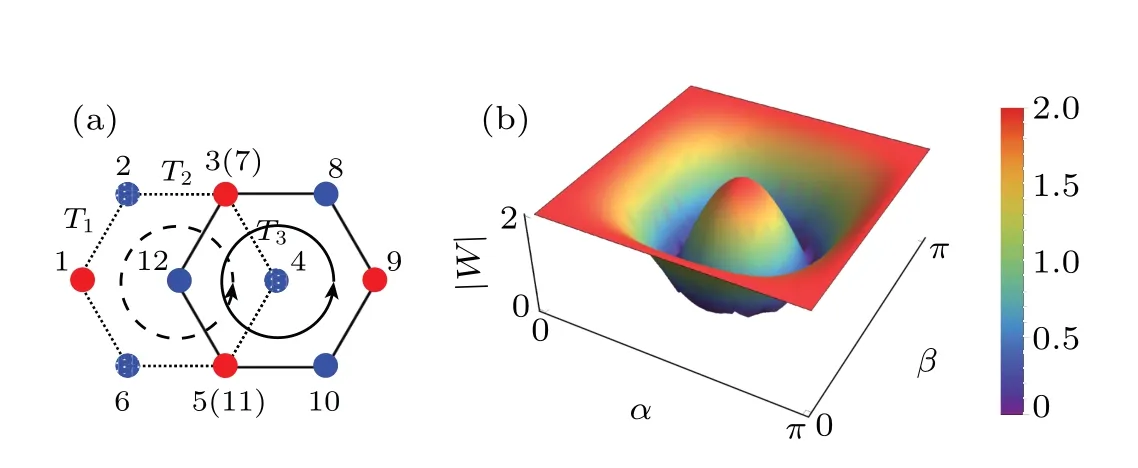
Fig. 2. (a) The illustration for the BHL subjected to the SU(2) gauge field. The odd(even)indices denote A(B)sites of the BHL.Subjected to SU(2)gauge field, the hopping integrals are dressed by T1 = eiατx,T2 = 1, T3 = eiβτy. (b) The magnitude |W| of the Wilson loop as a function of α and β in [0,π] range. The Abelian regimes include the four edges of α–β square and the center point (π/2,π/2), where|W(α,β)|=2.

3. Topological Lifshitz transition

For the graphene point (α,β) = (0,0), the Hamiltonian (9) is reduced to the Hamiltonian (2) with color degeneracy,

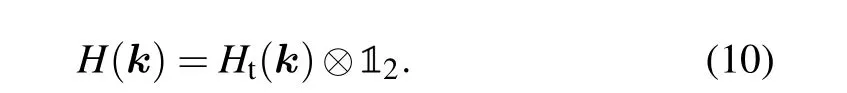
Therefore, the band structure at graphene point is the same with spectrum (3), except for the double degeneracy of each band[see Fig.3(a)].Consequently,the number of Dirac points increases fromN=2 toN=4. Then we consider the entire Abelian regimes.

Fig.3. Band structure of the BHL with SU(2)gauge potential for different fluxes (α,β). (a) Graphene point α =β =0. (b) π-flux pointα =β =π/2.

Comparing SU(2) gauge Hamiltonian (8) with Hamiltonian (1), we can easily find that the electron–hole symmetry persists against the gauge field. Thus, the spectrum modified by gauge potential is also symmetric around zero energy. Under these circumstances, all Dirac points can be identified by the zero energy modes of the uppermost valence band,which could be utilized to demonstrate the topologies of Fermi surfaces. Patterns of zero modes for different gauge fluxes(α,β)along the Abelian path(0,0)→(0,π)→(π,π)are shown in Fig. 4. The number of Dirac points is invariant in the trivial Abelian regimes and only their positions are transported in the momentum space by the Abelian gauge field. The positions of Dirac pointsP1andP2in the trivial Abelian regimes are determined by the following expressions:P3andP4are the space inversion ofP1andP2,respectively. If their coordinates exceed FBZ,these points must be translated into FBZ along reciprocal vectors.

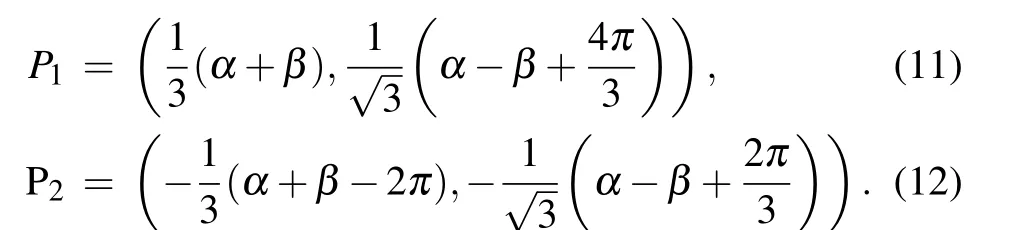
To illustrate the topological Lifshitz transition, a topological argument must be attached. The universality class of gapless excitations is determined by a topological winding number.[5,30,66]If the Hamiltonian satisfy a particle–hole symmetry{Γ,H(k)}=0,whereΓ=diag{12,-12,12,-12},we can define a local winding number

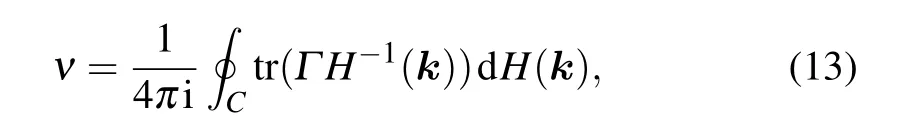
whereCis a loop surrounding the singularity in the momentum space.[30,66]For the honeycomb lattice with SU(2)gauge potential,the topological charges of massless Dirac points areν=±1.[30]For trivial Abelian regimes on BHL,there are two negative topological chargesν(P1) =ν(P2) =-2, and two positive onesν(P3)=ν(P4)= +2. Forπ-flux point, there are four positive topological chargesν(K′,Q2,Q3,Q6)=+2 and four negative topological chargesν(K,Q1,Q4,Q5)=-2.In this way,the universality classes of trivial Abelian regimes andπ-flux point are different, indicating a topological Lifshitz transition connecting these two phases driven by the non-Abelian gauge fluxes.[5]

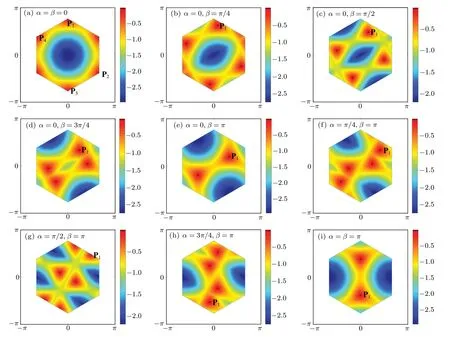
Fig.4. Topologies of Fermi surfaces for different gauge fluxes(α,β)along the Abelian path(0,0)→(0,π)→(π,π). In the trivial Abelian regimes,the number of Dirac points is invariant. The Abelian gauge field only changes the positions of these zero modes in momentum space.The position change of Dirac point P1 with fluxes(α,β)is shown in detail.

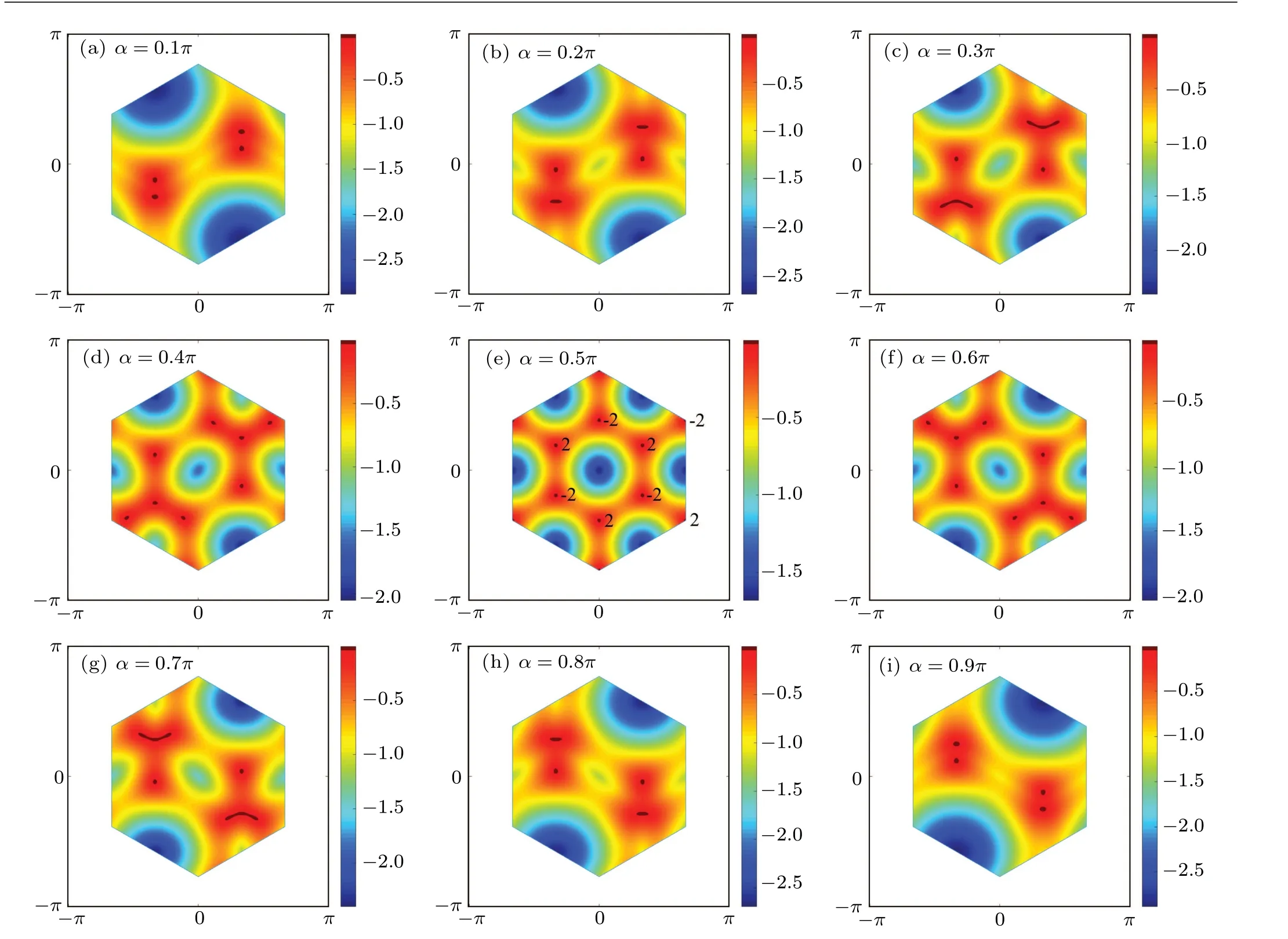
Fig.5. Topology of Fermi surfaces for different gauge fluxes(α,β)along the non-Abelian path(0,π)→(π,0),where β =π-α. There are four Dirac points in(a)–(b)and(h)–(i),which are the same with trivial Abelian regimes. Panels(c)–(g)belong to the N=8 phase.

4. Phase diagram

To investigate the topological Lifshitz transition thoroughly,we tune the gauge fluxes(α,β)along the non-Abelian path (0,π)→(π,0) and obtain the topologies of respective Fermi surfaces in Fig.5. We find that the region aroundπ-flux point is in theN=8 phase [Figs. 5(c)–5(g)]. It is necessary to obtain the phase boundary of the topological Lifshitz transition.

As we know, the energy bands can be obtained by solving the secular equation det[H(k)-E]=0. If zero modes exist,the equation det[H(k)]=0 will have roots,the number of which will equal the number of zero modes.Since the number of zero modes differs in the topological Lifshitz transition induced by non-Abelian SU(2)gauge potential,we can obtain the phase boundary by solving the equation det[H(k)]=0. It is easy to find that

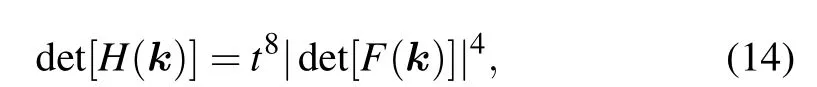
which is independent oft′. Thus the value oft′does not affect the phase transition. Therefore,the problem is reduced to solving the equation det[F(k)]=0.

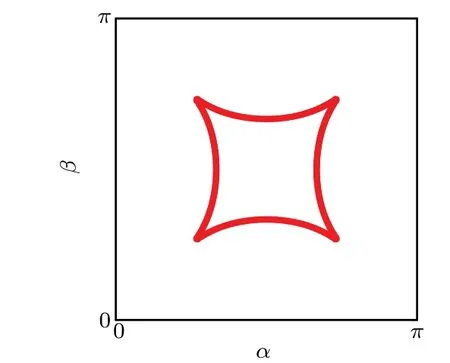
Fig.6. The α–β phase diagram. The phase boundary of the topological Lifshitz transition is the red line, which corresponds to Δ =0. There are N=4 Dirac points outside the boundary.

When the discriminantΔ=0,the corresponding equation has multiple roots. Consequently,we obtain the phase diagram of gauge fluxes(α,β)in Fig.6. The phase boundary of the topological Lifshitz transition is the red line,which corresponds toΔ=0. TheN=4 phase is outside the phase boundary,whileN=8 phase inside the boundary. The phase diagram can also be confirmed by calculating the Fermi surfaces.

5. Novel edge states

Different from honeycomb lattice,there are some unique phenomena on the BHL, which also exhibit exotic changes under the influence of SU(2) gauge field. Localized edge states have been reported to exist at the zigzag edges of bilayer graphene.[67]Now we begin to investigate the effects of the SU(2)gauge potential on the localized edge states. A tunable band gap has been realized by applying a biased electric field on bilayer graphene.[45–49]Hence we consider the biased BHL nanoribbon with zigzag edges [see Fig. 1(b)]. When a gated voltage is applied to BHL,the Hamiltonian(9)should be modified by adding a termHV=Vdiag{14,-14},where 2Vis the voltage difference between the two layers. A two-photon dressing field can be used to produce an effective gauge potential for neutral atoms. Through the time dependence of the effective potential,we can generate synthetic electric field on neutral atoms.[25]A generalization of Bragg spectroscopy can be used to detect edge states in optical lattices.[68]

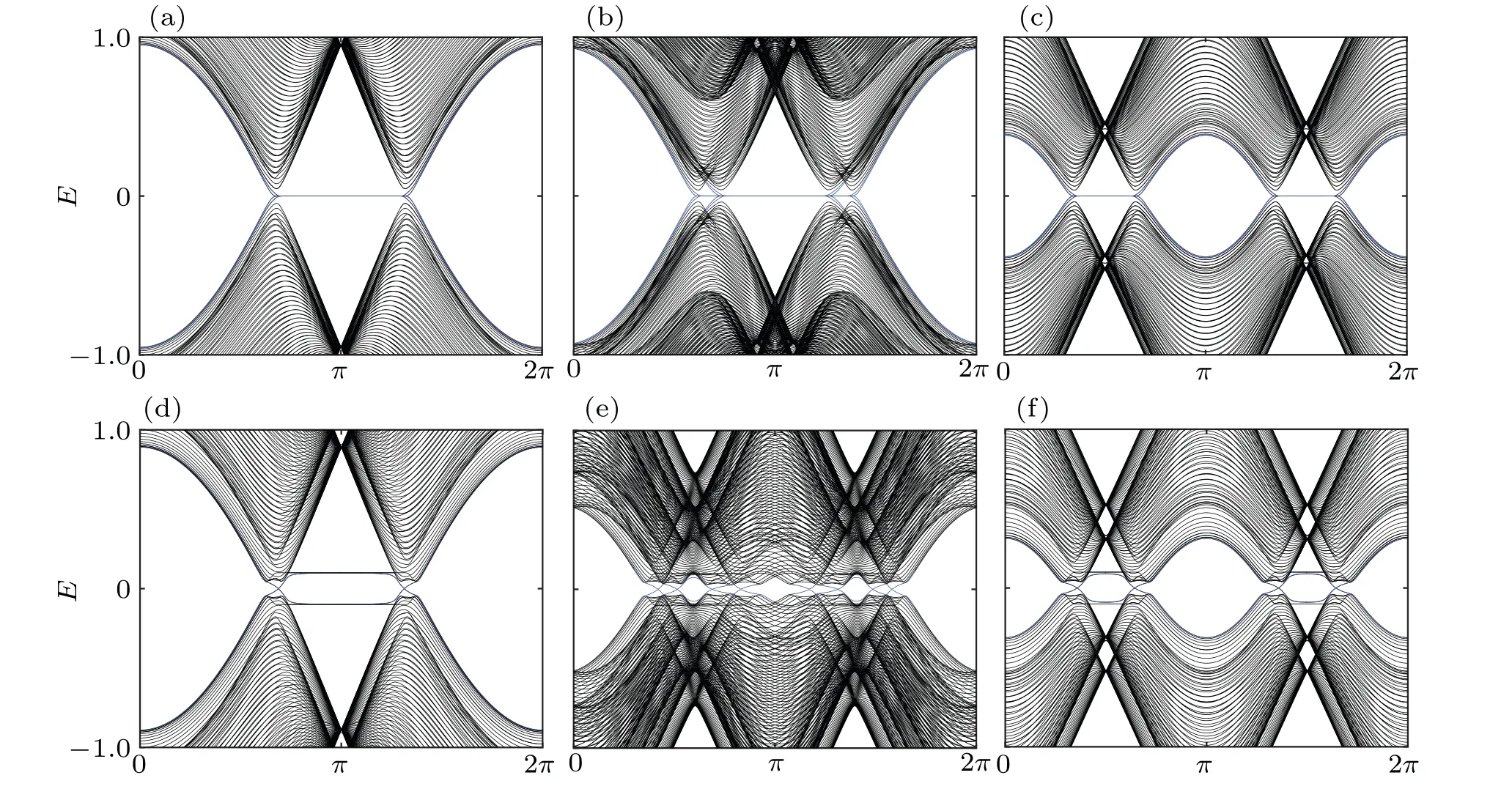
Fig. 7. Energy spectrum for a bilayer ribbon of NL =80 cells with zigzag edges. (a) V =0,α =β =0. (b) V =0,α =β =π/10. (c)V =0,α =β =π/2. (d)V =0.1,α =β =0. (e)V =0.1,α =β =2π/5. (f)V =0.1,α =β =π/2.

WhenV= 0, we tune the gauge fluxes (α,β) along(0,0)→(π/2,π/2). Four partly flat bands at Fermi level locate in the range of[2π/3,4π/3][Fig.7(a)],which correspond to four edge states.[67]As we know,these bands are doubly degenerate and the increasing flux will result in a nondegeneracy.We can find that four additional dispersive bands appear away from the flat bands in Fig.7(b). The nondegenerate flat bands are also transported by gauge fluxes in momentum space and thus their range is also enlarged. When the fluxes continue to increase, the nondegenerate flat bands will separate into two parts.Finally,forα=β=π/2,the nondegeneracy disappears again,but the two parts of flat bands remain in Fig.7(c).

Considering biased voltageV= 0.1, we show the energy spectrum of a bilayer ribbon for different gauge fluxes in Figs.7(d)–7(f). The bias will move two flat bands from Fermi level toE=±V, and the other two edge states become two dispersive bands crossing the opened gap[Fig.7(d)]. Similar to the unbiased case, the SU(2) gauge potential will destroy the color degeneracy and transport the bands. As a result,we can see eight band crossing in the gap whenα=β=2π/5 in Fig.7(e). Atπ-flux point,both the flat and crossing bands separate into two parts[Fig.7(f)].

6. Summary

In this work,we systematically study the SU(2)gauge effects on BHL. Based on the tight-binding model of graphene bilayer,we deduce the model by Peierls substitution. A topological Lifshitz transition induced by the non-Abelian gauge potential is discovered. Topological Lifshitz transitions are identified by the topologies of Fermi surfaces. The Fermi surface atπ-flux point consists ofN=8 Dirac points,instead ofN=4 in the trivial Abelian regimes. We also define a local winding number to classify the universality class of different topological phases. Then the phase diagram of gauge fluxes is demonstrated. The influence of gauge potential on edge states of biased bilayer ribbon is investigated. At the end,we would like to emphasize that the gauge potentials of different layers are independent in the present work,and the interlayer gauge fields cannot be considered. If we consider the interlayer gauge fields,the problem would become much more sophisticated and interesting,which will be studied in the future.In conclusion,our work will contribute to the research of topological Lifshitz transition and SU(2) gauge effects on bilayer honeycomb lattice. And the comprehension will be helpful for the electronic applications of bilayer graphene.

Acknowledgements

We are grateful to X.D.Zhang,F.Sun,D.Y.Jing,and J.K.Wang for helpful discussions.

This work was supported by the National Key R&D Program of China (Grant Nos. 2021YFA1400900,2021YFA0718300, and 2021YFA1400243) and the National Natural Science Foundation of China(Grant No.61835013).