Chiral splitting of Kondo peak in triangular triple quantum dot

Yi-Ming Liu(刘一铭) Yuan-Dong Wang(王援东) and Jian-Hua Wei(魏建华)

1Department of Physics,Renmin University of China,Beijing 100872,China

2School of Electronic,Electrical and Communication Engineering,University of Chinese Academy of Sciences,Beijing 100049,China

Keywords: Kondo effect,quantum dot,chiral splitting

1. Introduction

As discussed by Berry,[1]the wave function acquires geometric phase, Berry’s phase, when it is adiabatically moves along a circuit in the Hamiltonian parament space. In metallic magnets, a complex factor occurs when electrons hop along the noncoplanar spin configurations, resulting in spin chirality.[2]The phase is the vector potential generated by electron spins,and corresponds to the Berry phase experienced by hopping electrons. Consider an electron hopping along a loop 1→2→3→1, the total phase acquired by the electron is the solid angle subtended by the three spinsSi(i=1,2,3)and is proportional to the spin chiralityS1·(S2×S3). Such a gauge flux acts as a fictitious magnetic field and affects the charge dynamics as the real magnetic field, which is an important physical phenomenon in strongly correlated electronic systems.[3–6]

The Kondo effect[7]reflects the low energy many-body correlation of electrons, which describes the local moment screening of an isolated electron by the itinerant electrons via an antiferromagnetic interaction at low temperatures; which has been the core of theoretical and experimental investigations for several decades,[8]especially the experimentally observed Kondo effect in nanostructures[9–11]and theoretical studies in magnetic field.[12]Moreover, quantum dot devices are particularly suitable for studying the Kondo effect owing to the strong operability. Especially the triple quantumdot system, which present various Kondo effects depending on magnetic field,[13,14]electron fillingNtot,[15,16]quantum phase transition,[17–19]and low-energy electronic transport properties.[20–28]

In a ring-like TTQD structure, spin chirality is induced by the noncoplanar spin configuration. Existing studies show spin chirality has been applied to quantum computation by spin cluster qubits[29,30]in TTQD system. In addition, the spin Berry phase has profound significance in gauge theory of strongly correlated electronic systems. For example, the anomalous Hall effect(AHE)observed in colossal magnetoresistance manganites is a manifestation of the Berry phase effect, which is caused by carrier hopping within a nontrivial spin background;[31]and the one that bias-induced chiral current in TTQD system.[32]This makes a difference by considering spin chirality as a new factor in TTQD system. Therefore,the spin chirality entangling with Kondo effect at low temperature is expected to induce nontrivial physical phenomenona.Insight by the above developments, we investigate the influence of spin charity on Kondo effect in TTQD system.

The TTQDs structure comprise three triangularly configured and coupled quantum dots with one dot(defined as QD1)connected to one electron reservoir. Three quantum dots are coupled through tunneling strengthtwith single occupation on each dot(Fig.1). The Hamiltonian of TTQD is described by Anderson impurity model. In absence of external field and electron reservoir,the spin alignment is coplanar,so spin chirality is degenerate. The four-fold degenerate chiral states|q〉comprise the ground states of isolated TTQD. At same time,the Kondo screening occurs between QD1 and itinerant electrons of noninteracting electron reservoir via an antiferromagnetic interaction in the equilibrium state at low temperature. A corresponding Kondo peak appears aroundA1(ω=0)(Fig.2(b))in the spectral function of QD1,which is attributed to electrons tunneling between four-fold chiral ground states,one is induced by virtual processes of the excited state. As tunneling strengthtincreases, the Kondo peak splits into bimodal peaks with a split space of 3/2J(J～4t2/U),indicatingt-induced antiferromagnetic interactionJ. Analogous Kondo peak splitting caused by interdot tunnelingtin coupled double quantum dots.[33]Moreover,particle–hole asymmetry appears with increasing tunnelingt. We apply a perpendicular magnetic field to restore particle–hole symmetry of TTQD system.is seldom studied in TTQD system. Such innovation of the Kondo physics motivates us to study a triangular triple quantum dot (TTQD) as the simplest multiple QD system with a closed loop. This work indicates the phase factor under magnetic field introduces new features into low energy quantum transport in strong correlated systems and the numerical results provide a detailed understanding of physical characters for the implementation in experiment.

Fig. 1. Geometry of TTQD. The electrons circle around TTQD structure,which generates two equivalent directions of chiral ring current. The sign(+)in black denotes the clockwise direction,(-)represents the anticlockwise direction. QD1 is connected to the electron reservoir by coupling strength Δ =0.5 meV and the same tunneling strength t between three dots to hold C3v symmetry. Chiral spin states for (a) |〉, (b) |q〉, (c)

2. Model and methods

Under perpendicular magnetic field, the virtual current moving around magnetic flux enclosed TTQD loop induces the Berry phase in real space, that is Aharonov–Bohm phase.[34]Existing results show perpendicular magnetic field splits the degeneracy of left- and right-hand chiral states|q±〉[32,35,36]in TTQD geometry. The chiral interaction induced by the magnetic flux forms a non-coplanar spin texture with spin chirality,leading to chiral splitting of the Kondo peak. The chiral splitting is contributed by the electron hopping between two chiral state pairs|q±〉, which is produced by phase (φ)-dependent chiral interaction coefficientχ. Numerical calculation results show there has a linear relationship between the space of splitting chiral Kondo peak and chiral interaction coefficientχ. Furthermore,when applied Zeeman magnetic fieldBas well as perpendicular magnetic field,chiral Kondo peaks split into four peaks owing toBlifts the degeneracy of spin freedom. Quantum fluctuations between both spin and chiral orbital degrees of freedom cause an exotic SU(4) Kondo effect at low temperatures, which manifests as four-peak splitting. A similar SU(4) Kondo effect has been reported in carbon nanotubes.[37,38]The influence of spin chirality on the Kondo effect indicates a core role of the phase factor in TTQD system. Some studies show the phase is a key factor effect on the bias-induced chiral current[32]as well as chirality-based coded qubit in TTQD,[30]while the spin chirality produced by phase further effect on the Kondo effect

The HEOM approach investigates the properties of quantum dots in both equilibrium and non-equilibrium states via the reduced density operator, which has a universal formalism for an arbitrary system Hamiltonian; thus, it can be used to accurately solve the three-impurity Anderson model. The detailed derivation for the HEOM approach is shown in Appendix A and Refs.[39,40],and the final form can be reduced to the following compact form:

The HEOM approach is established based on the Feynman–Vernon influence functional path-integral theory[41]and implemented with Grassmann algebra for fermion dissipations.[42]Basically, the HEOM approach is a nonperturbative method for general quantum systems coupled to reservoir that satisfies Grassmann Gaussian statistics.[42–44]Based on the linear response theory of quantum open systems,it can accurately and efficiently obtain a dynamical observable quantity of strongly correlated quantum impurity systems.[39]In practical calculations,we must minimize the computational expenditure while maintaining the quantitative accuracy. For this purpose, we usually impose a truncationLas the highest tier of the ADOs. This truncation decreases the number of EOMs to match the insufficient calculation capacity, without affecting the nonperturbation characteristic of HEOM. This truncationLis measured by the quantitative convergence atA(ω=0)when the Kondo effect is considered,usuallyL=4 for most physical cases. However, lower temperatures demand a higher truncation tier and more computing resources to achieved numerical convergence. In recent years,HEOM has been widely used to investigate the Kondo effect and transport properties under equilibrium and non-equilibrium conditions in quantum dot systems.[33,45–48]

3. Results and discussion

When perpendicular magnetic field applied, magnetic flux threads the TTQD structure,thet–J–χmodel can be derived by treatingtinHdotsperturbatively[32,49]

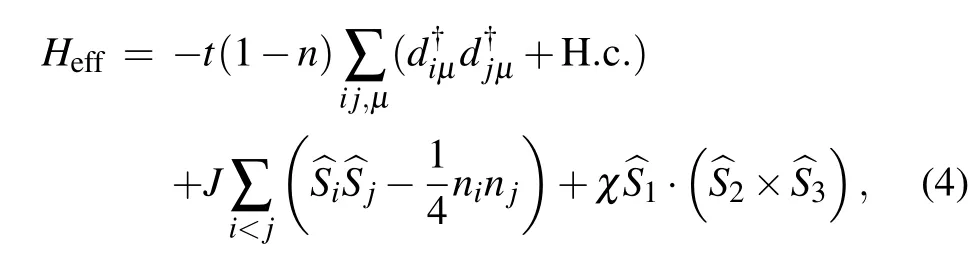
In equilibrium state, the Kondo effect in absence of perpendicular magnetic field is similar to the Kondo peak splitting in double quantum dots;[33]which is a process ofJinduced Kondo splitting. Figure 2(a) shows the schematic diagram of the splitting of Kondo peak, which depicts the electron spin flip through virtual state; this is aided by the electron bath, from singlet to triplet. The lateral peaks (denoted as blue dotted line arrow) appear with an increase in tunneling(t)-dependent antiferromagnetic strengthJbetween quantum dots. Theoretically,the difference in eigenvalues between|Q〉and|q〉is 3J/2,J～4t2/U. Electron hopping between four-fold ground states|q〉and excited states|Q〉contributes to lateral peaks in Fig.2(b).The distance between two splitting Kondo peaks are linear with respect toJ[shown in Fig. 2(c)]. And electron hopping between four-fold degenerate states|q〉contributes to the prime Kondo peak, which is shown in Fig.2(b).

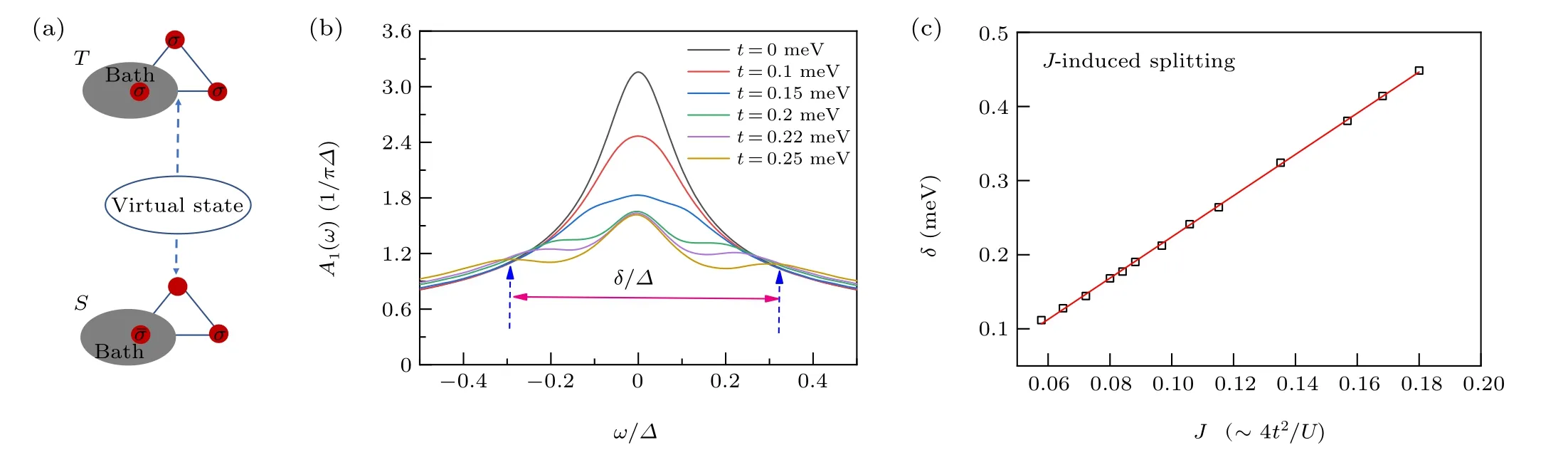
Fig. 2. (a) Schematic diagram of J-induced Kondo peak splitting; electrons in two arbitrary quantum dots participate in the process of Kondo resonance through virtual state;the shadow part is the electron bath and σ =↑or ↓;T denotes the triplet;S is the singlet. (b)Spectral density functions A(ω)of QD1 with an increasing tunneling strength t without any magnetic field. A1(ω)=2A1↑(ω)=2A1↓(ω). The blue dotted line arrow points to lateral peaks,and δ/Δ is the distance between two lateral peaks. (c)The scatter combined with the line shows that the space of the two splitting Kondo peaks is exactly linear with respect to J,which is induced by the antiferromagnetic interaction J.

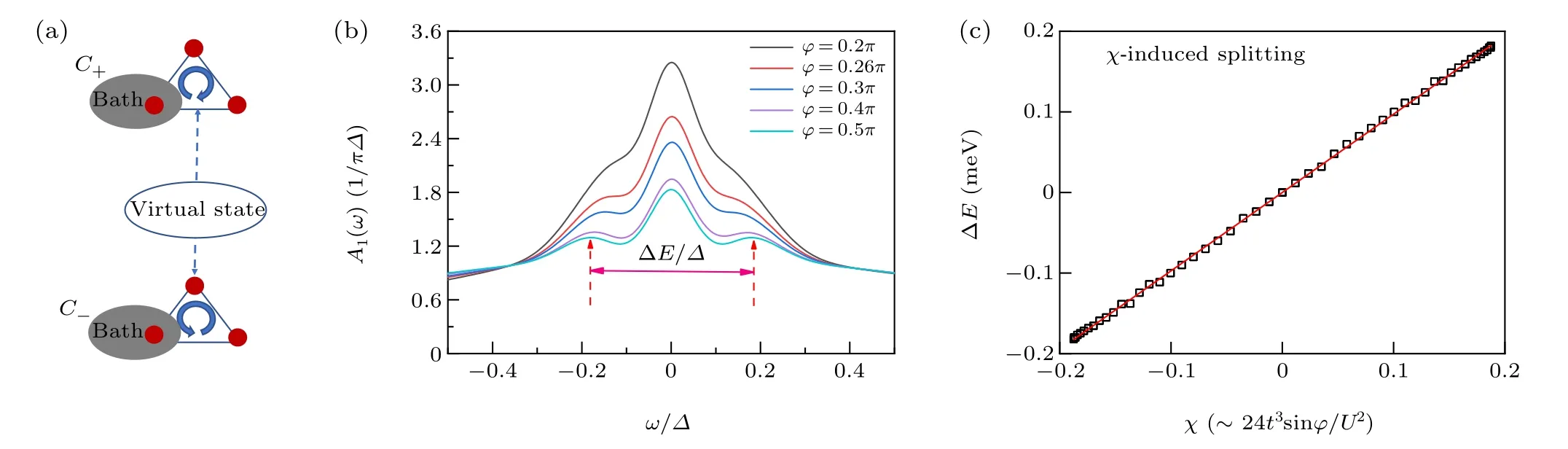
Fig.3. (a)Schematic diagram of chiral splitting of Kondo peak. C+ denotes right-hand chiral states|〉/|〉, and C- denotes left-hand chiral states〉/|〉. The sign of clockwise and anticlockwise arrows corresponds to spin circling directions. (b)Spectral density functions A(ω)of QD1 with an increasing phase φ under a perpendicular magnetic field. A1(ω)=2A1↑(ω)=2A1↓(ω). The red dotted line arrow points to two splitting chiral Kondo peaks,the distance between them is ΔE/Δ. (c)The scatter combined with the line shows that the space of chiral Kondo splitting is exactly linear with respect to χ,which is as function of φ. The TTQD parameter is t=0.25 meV.

When a perpendicular magnetic field is applied,a fluxφthreads the ring like TTQD structure; the correspond phaseφimpact on tunneling strengthtresults a chiral operator^S1·(^S2×^S3).The chiral operator splits the degeneracy of fourfold ground states into two pairs of chiral states,which are leftand right-hand chiral states. Figure 3(a) shows that the fourfold ground state|q〉splits into two chiral state pairs,which are denoted asC+(right-hand chiral states)andC-(left-hand chiral states); but remain the degeneracy of spin freedom. And the transition fromC-toC+through virtual state, attributes to splitting of chiral freedoms, i.e., chiral splitting of Kondo peak,which are denoted asC+(right-hand chiral states) andC-(left-hand chiral states);but remain the degeneracy of spin freedom. And the transition fromC-toC+through virtual state,attributes to splitting of chiral freedom,i.e.,chiral splitting of Kondo peak.

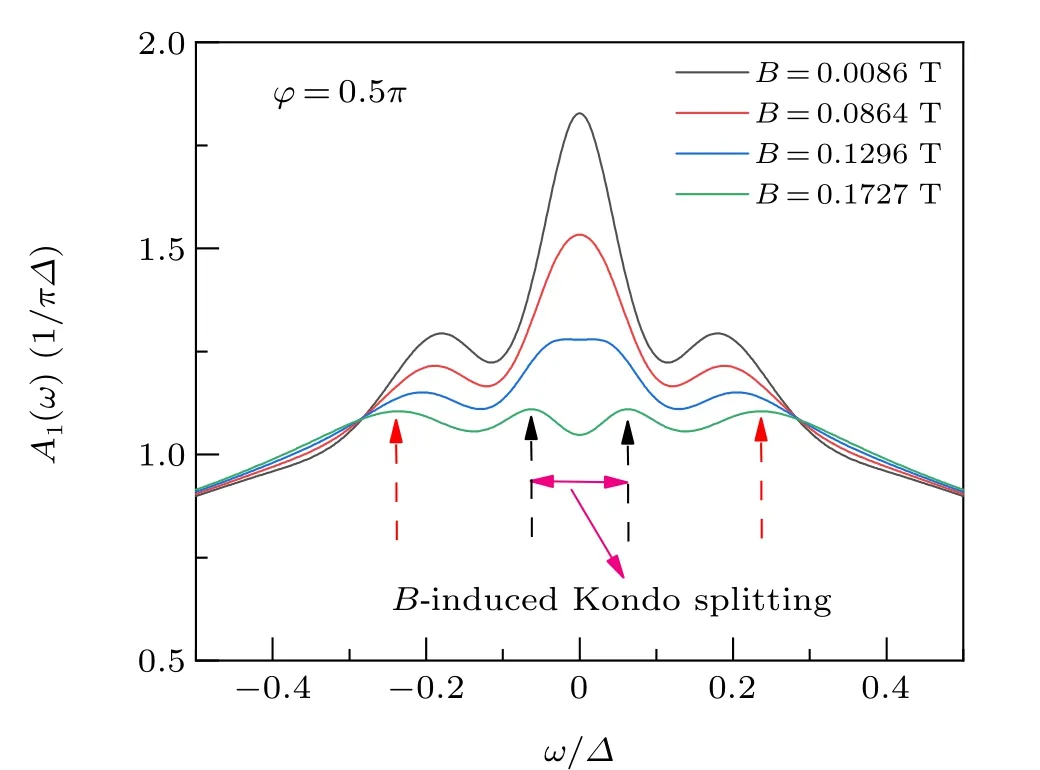
Fig. 4. Spectral density functions A(ω) of QD1 with increasing Zeeman magnetic field B;A1(ω)=A1↑(ω)+A1↓(ω). We calculated at φ =π/2 under applied perpendicular magnetic field at t =0.25 meV. The black dotted arrows denote the splitting of spin freedom of Kondo peak, which induced by the Zeeman magnetic field B;the red dotted arrows denote chiral splitting of Kondo peak.

Finally, when transverse magnetic fieldBapplied to the TTQD structure with phaseφ=π/2, the chiral Kondo peak still exists at small magnitudeB, as shown in Fig. 4; with an increase inB, the chiral Kondo peaks split into four peaks,which is shown inB=0.1727 T.Inter peak(denoted as black dotted line)splitting is induced byB,which means the splitting of spin freedoms of two degenerate chiral state pairs. Analogous situation is the SU(4) Kondo effect observed in carbon nanotubes;[37,38]but the magnetic moment of orbital in carbon nanotubes originate from the two equivalent ways in which electrons can circle around the graphene cylinder; while in TTQD structure, the orbitals stem from the chiral spin states caused by the many-body interactions; and the many-body spin states is closely related to superconductivity.[4]Additionally,the Kondo peak is broken into two peaks with an increase inBwithout a perpendicular field in Appendix B.

4. Conclusion

In summary, we investigate new characteristic of the Kondo effect caused by the spin chirality arising from the phase factor in the TTQD structure in the equilibrium state.Under a perpendicular magnetic field,a fluxφthreads TTQD,lifting the degeneracy of left-and right-hand chiral state pairs|q±〉. Moreover,the chiral splitting of Kondo peak(Fig.3(b))can be explained by electron hopping between two chiral state pairs. The particle–hole revive symmetry by adjusting magnitude of fluxφ=π/2. The numerical simulation results in agreement with analytical results(Fig.3(c)). Furthermore,the Zeeman magnetic fieldBlifts the spin freedom degeneracy of chiral state pairs, leading to splitting of four peaks(shown in Fig. 4) under perpendicular magnetic field conditions. This work indicates the phase factor plays a core role in introducing new features into Kondo effect in strong correlated systems and the numerical results provide a detailed understanding of physical characters for the implementation in experiment.

Acknowledgments

Computational resources have been provided by the Physical Laboratory of High Performance Computing at Renmin University of China. Project supported by the National Natural Science Foundation of China (Grant Nos. 11774418,11374363,and 21373191).

Appendix A:HEOM approach

The HEOM approach is established based on Feynman–Vernon influence functional path-integral theory[41]without any approximations, and implemented with Grassmann algebra for fermion dissipations.[42]Basically,the HEOM is a nonperturbative method for general quantum systems coupled to reservoir baths those satisfy Grassmann Gaussian statistics.The reduced density matrix and a set of auxiliary density matrices are the basic variables in HEOM. Basing on the linear response theory of quantum open systems,the HEOM can obtain dynamical observables of strongly correlated quantum impurity systems accurately and efficiently.[39]In recent years,the HEOM approach has been widely used to investigate the Kondo effect and transport properties under equilibrium and non-equilibrium conditions in quantum dots.[33,46,47,50–52,54]

Comments on the HEOM approach

The main advantages are as follows: (i) the HEOM approach adopts a general form of the system Hamiltonian. It is applicable to a wide range of system parameters without additional derivation and programming efforts. The different transport processes can be handled in a unified manner and the transient dynamics can be studied readily;(ii)the HEOM approach is nonperturbative. It treats quantum impurity systems from the perspective of open dissipative dynamics. In principle, the HEOM formalism is formally accurate for noninteracting electron reservoirs. It also resolves non-perturbatively the combined effects of electron–electron (e–e) interactions;(iii) in HEOM all the system-bath correlations are taken into consideration. It is capable of characterizing both static and transient electronic properties of strongly correlated systems;and(iv)the HEOM is a high-accuracy numerical approach. It has the ability to achieve the same level of accuracy as the the numerical renormalization group(NRG)and quantum Monte Carlo approaches.

The disadvantages for HEOM approach are mainly shown as follows: (i) it can only deal with the case of finite temperatures, while the zero temperature is inaccessible; (ii) a higher truncation level is necessary to ensure numerical convergence at an extreme low temperature,this leading to a rapid growth of the required computational resources;(iii)the computation cost increases dramatically as the degree of system increases. For example, we can not reach the problem that a quintuple-impurity Anderson model with strong e–e interactions at present.

As a successful application, the HEOM approach has been proved to be capable of quantitatively describing the essential signatures of Kondo physics[33,39,46,48]and achieving the accuracy of the NRG approach.Currently for a typical Anderson model,the HEOM approach reaches quantitatively accuracy for temperatureT ≥0.1TK(Kondo temperature). Here,we show the benchmark scaling character and spectral features of the Kondo effect in single-impurity Anderson model(SIAM). Figure A1 indicates the HEOM results exhibit the correct scaling behavior by Kondo temperatureTK. By referring to the calculated dI/dVversusT/TKas depicted in Fig.A1,the universal scaling is clearly manifested atT ＜TKandΔ ≪U ≪W(whereΔis the hybrid function andWis the band width of itinerant electrons). It is clear at low temperature(T ＜TK),no matter of our parameters,the results of differential conductance fall on one line,which characters the Kondo effect.For unscaledT,we draw it in the inset(for more details,please refer to Ref.[39]).

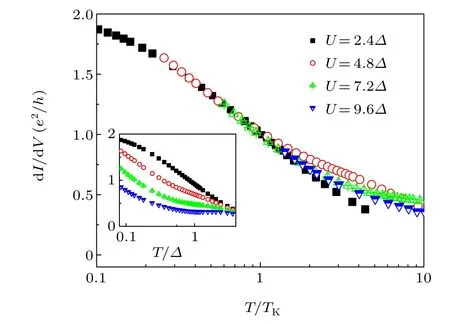
Fig.A1. The dI/dV calculated by HEOM vs. T/TK for symmetric SIAM.The inset depicts dI/dV vs. unscaled T.

Figure A2 depicts the calculatedA(ω) of a symmetric SIAM,from weak(U=0.5πΔ)to strong(U=6πΔ)e–e interactions. For comparison,we also show results obtained by using the full density matrix NRG method,where a self-energy scheme is employed, and the results are averaged over 8 different logarithmic discretization. Apparently, the two sets of curves agree quantitatively at all values ofUstudied. In the weak(U=0.5 and 1.0πΔ)and intermediate(U=3πΔ)interaction regimes, HEOM and NRG curves almost overlap with each other;while in the strong(U=6πΔ)interaction regime minor deviation is observed in the height of Hubbard peaks(for more details,please refer to Ref.[39]).

As aforementioned, the HEOM approach has been applied to investigate the Kondo effect in different QD structures. For example, Yeet al.applied it onto two-level QDs with Kondo correlations, providing an understanding of, and a viable mechanism for controlling,the thermoelectric properties of strongly correlated QD systems.[53]In coupled double QDs,Liet al.studied the Kondo-peak splitting and resonance enhancement caused by inter-dot tunneling;[33]Chenget al.investigated transport properties in the real-time domain;[54]and Panet al.studied the Kondo effect in the context of ferromagnetic RKKY interaction.[55]Recently, in open triple QDs,Chenget al.investigated the reappearance of the Kondo effect[45]and long-range overlapping of Kondo clouds.[48]

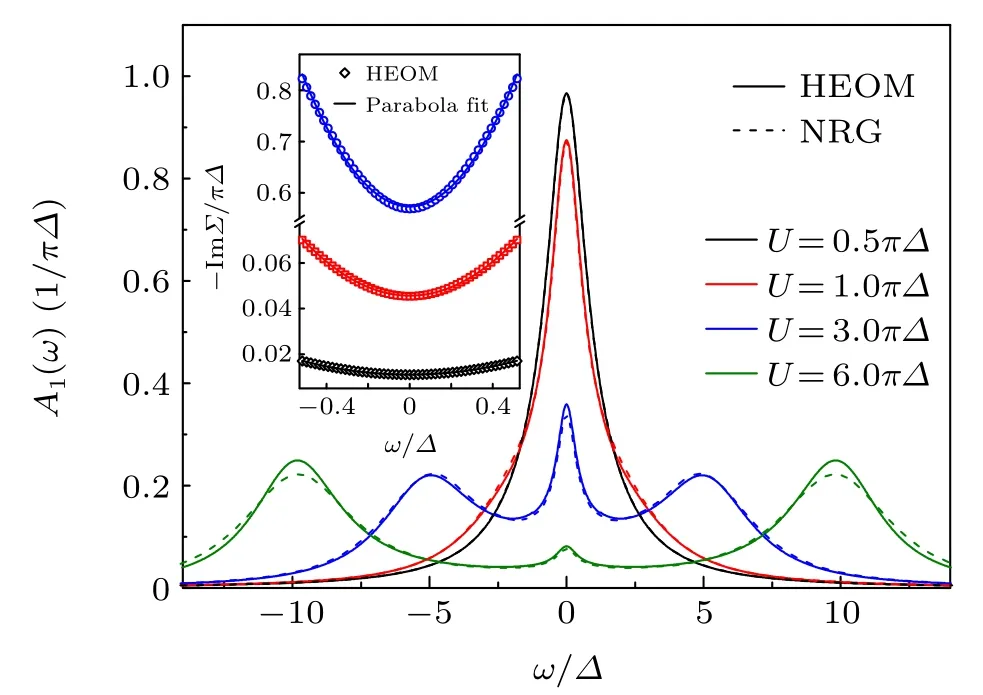
Fig. A2. Comparison between A(ω) of symmetric SIAM calculated by HEOM and NRG methods. The parameters adopted are T =0.2 and W =50(in units of Δ). The inset shows the imaginary part of interaction self-energy calculated from HEOM at energy close to ω =0.

Appendix B: Some supplementary information about the physical image

Figure B1 depicts the spectral density functionsA1↑(ω)in the absence of external magnetic field with the increase of tunneling strengtht. The spectral density functions is shifting left with the increasingt,which means the electron–hole is asymmetry. And we can recover the symmetry of electron–hole by applied a perpendicular magnetic field to the TTQD structure.We adjust the flux atφ=π/2 with the increasing tunneling strengthtin the right part of Fig. B1, and the electron–hole recover to symmetry.

Fig.B1. (a)The A1↑(ω)as function of ω with the increase of t; and A1(ω)=2A1↑(ω)=2A1↓(ω). (b)The A1↑(ω)calculated by HEOM versus ω/Δ with the flux φ =π/2.

Fig.B2.(a)Theχand ΔE asfunctionofφin twoperiods.The dottedline inreddenotesthetheoreticaldeduceχ andthelineinblack isthenumerical computationΔE[we set2/ΔE forsimplifciation]. (b)TheA1↑(ω)asfunctionofω/Δwith the increaseofflux φ;A1(ω)=2A1↑(ω)=2A1↓(ω).We calculate at t=0.25 meV.

The left part of Fig. B2 depicts the comparison for the numerical computation and theoretical deduce about distance between two lateral peaks[in Fig.3(b)of the main text],which as function of the fluxφwith a perpendicular magnetic field.The periodic variation of the curve with the fluxφis adjustable; the difference between two curves derives from the non-perturbation computing method. And the right part of Fig.B2 depicts the spectral density functionsA1↑(ω)with the increase of fluxφin half period when applied perpendicular magnetic field to the TTQD structure. The lateral peaks is expanding with the increase of flux; and the distance between two lateral peaks is linear fitting well with the equationχ～24t3sin(φ)/U2.

Figure B3 depicts the spectral density functionsA(ω)of QD1 with the increasing Zeeman magnetic fieldBin the absence of perpendicular magnetic field.With the increase of the Zeeman magnetic fieldB,the spectral density functions splits into two peaks, from Kondo resonance peak [in the Fig. 2(b)of main text],which means the splitting of spin freedom.

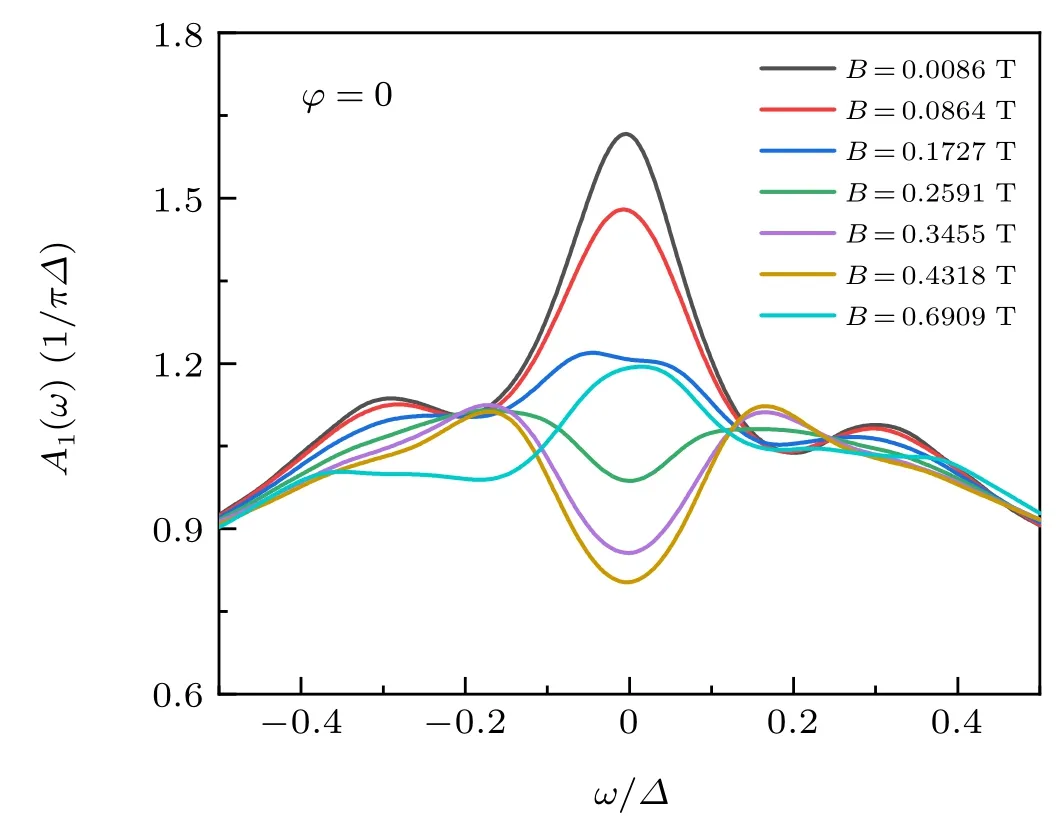
Fig.B3.The influence of Zeeman magnetic field without perpendicular field.A1(ω)as function of ω/Δ with the increase of Zeeman magnetic field B.