大型泵站水泵机组振动信号滤波方法

唐荣桂，邵知宇，樊锦川，张 炜，唐鸿儒

(1.江苏省农村水利科技发展中心，江苏 南京 210029；2.扬州大学电气与能源动力工程学院 江苏 扬州 225009；3.江苏泰州引江河管理处，江苏 泰州 225321)

水泵机组是水利枢纽工程的核心设备，其运行时的振动信号是反映设备健康状态的核心指标。引起水泵机组振动的因素主要包括转子、主电机输出轴和水泵轴不对中、叶轮碰磨泵壳、水流紊乱、电磁不平衡等[1]，这些原因引起的振动可以反映在振动信号的波形、频谱、轴心轨迹上。但是，泵站现场的主电动机(通常是10 kV左右的高压电源)、交流电动机、变频设备等可能形成电磁干扰，从而对测量振动的传感器微弱信号造成干扰[2]，因此采用滤波方法对泵站机组振动测量的信号进行抗干扰处理是关键步骤。在此基础上，振动信号的极值、均值、趋势等可用于设备状态评价和评估，为实现智能泵站建设中的水泵机组预测性检修奠定基础。

经典数字滤波器滤波是水泵机组振动信号处理中最常用、最基本的方法，包括无限脉冲响应数字滤波器(IIR)和有限脉冲响应数字滤波器(FIR)[3]。经典数字滤波器各有特点，如巴特沃斯滤波器在带通范围内具有非常平稳的幅值响应曲线，切比雪夫滤波器幅值响应具有较快的衰减速度。早期的水泵振动信号采集与监测系统大多采用经典数字滤波器处理水泵机组信息，如刘亚峰等[4-5]基于LabView的监测系统，骆寅等[6]的基于无线传感网络的监测系统等。然而随着泵站机组设备的智能化、复杂化，在实际工况中，经典数字滤波器滤波结果的相位时延、滤波不彻底等带来的问题在泵站机组状态监测中越来越突出。因此，随着滤波器的发展，其他研究领域的各种现代滤波器越来越多地被应用于水泵机组信号处理中，其中基于小波分析的方法应用最为广泛。张飞[7]较早对小波分析在水电机组状态监测与故障诊断中的应用进行了详细研究，并给出不同应用场景下的最佳小波基和阈值策略；潘天航等[8]研究小波分析应用于某机组机架振动去噪时的参数优选方法；胡道达等[9]针对机组振动的非线性和非平稳特征，引入小波包分型技术对机组常见故障类型进行了分析。近年来，基于谐波小波分析的方法也越来越多应用在旋转类机械故障诊断中，该方法以小波为基底进行线性转换[10]，结合了短时距傅立叶变换和连续小波转换两者的优点，具有严格的盒型特性[11-12]，解决了传统傅里叶变换不能用于非平稳信号、不能同时进行时频局部化分析等难题[13], 被大量应用在信号处理、模式识别等领域[14]。

综上，各种传统或者现代的滤波方法各有其优点和不足，如何根据具体的工况环境和应用场景下水泵机组的振动、摆度等信号的特点，选取合适的滤波方法尤为关键。为了进一步确定具体工况和应用场景下更为合适的滤波方法，本文以南水北调东线某站水泵机组运行时机泵联轴器处的振动信号为例，分别使用几种典型的滤波方法进行数据预处理并对结果进行对比分析。

1 典型滤波器原理与设计

1.1 工程场景概况

本文研究的泵站机组为立式全调节混流泵，10 kV同步电机功率为3 400 kW，转速为125 r/min，水泵叶轮直径为2.95 m，设计扬程为7.6 m，设计流量为33.4 m3/s。已知水泵机组转速为125 r/min，则机组振动信号的主频为2.08 Hz，考虑叶轮、导叶等因素，水泵机组的主要振动信号的频率在1～30 Hz之间。干扰振动信号主要为电机电源的50 Hz交流电及其相关的谐波信号。机组状态监测系统采集的联轴器处x、y方向原始的振动信号波形和轴心轨迹见图1，采样频率为1 024 Hz。

图1 联轴器处振动信号滤波前原始数据

1.2 滤波器原理与设计参数

分别采用巴特沃斯滤波器、基于汉宁窗的FIR滤波器、基于谐波小波滤波3种方法对同一组振动信号数据进行滤波处理，对比分析3种滤波方法的效果。

1.2.1基于巴特沃斯滤波器的信号滤波

IIR数字滤波器的N阶差分方程如下[3, 15]：

(1)

式中：x(n)为巴特沃斯滤波器待滤波的序列；y(n)为巴特沃斯滤波器最终的滤波结果；a、b为滤波器系数；M为非递归滤波器的阶数；n为序列长度。

差分方程中的各个参数通过设计巴特沃斯低通滤波器进行确定。为了克服泵站机组50 Hz交流电的干扰，选用巴特沃斯二阶低通滤波，截止频率选为40 Hz。利用matlab滤波器设计工具确定滤波器参数a1= -1.826 8、a2=0.840 7、b0=0.003 5、b1=0.006 9、b2=0.003 5。

1.2.2基于汉宁窗的FIR信号滤波

针对IIR数字滤波器存在不稳定和非线性相位的缺点，可以采用FIR滤波器。但是，为了克服FIR的采样序列是无限的特点，采用时域加窗的设计方法，通过有限长的窗函数序列截断理想滤波器的无限长序列，得到所期望的有限长FIR滤波器单位冲激响应，常用的窗口函数有矩形窗、三角窗、汉宁窗等。其中汉宁窗相当于三部分矩形窗频谱相加，可以使旁瓣互相抵消。采用汉宁窗函数滤波，可以使信号集中在主瓣，减小水泵机组振动中高频干扰和漏能。

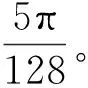
1.2.3基于谐波小波的振动信号滤波

除了巴特沃斯IIR滤波器具有非线性相位延迟和基于汉宁窗的FIR滤波器具有线性相位延迟外，2种滤波器的频域都有过渡带，且存在频谱泄露的可能。因此，Newland[16]提出了基于谐波小波的滤波方法，具有严格的盒型特性，使其能够无限细分截取任意频段的信号，其频域表示为

(2)

其时域表示为

(3)

式中：W(ω)为信号在频域内傅里叶变换的结果；ω为角频率；p为频段的起始频率；B为带宽。

实际应用过程中，其原理是将需要滤波的序列x(n)与谐波小波ω(n)在时域内的结果进行卷积，保留想要获得的频段：

(4)

式中：x(n)为谐波小波滤波待滤波的序列；y(n)为谐波小波滤波最终的滤波结果。

根据泵站工程场景特点，水泵机组主要振动信号的频率在1～30 Hz之间,且需要排除来源于电机电源50 Hz交流电及其相关的谐波信号的干扰。因此，谐波小波的目标是保留0～40 Hz的信号，据此滤波器设计中可取p=0 Hz,B=40 Hz。

2 滤波结果对比分析

由图2和图3可知，巴特沃斯滤波器对于机组振动信号具有较好的低通滤波效果，40 Hz以上的噪声基本被滤除。但从图2中不难看出，联轴器处x、y方向的滤波结果存在非线性相位延迟的问题，且轴心轨迹图中存在到中心区域的连线，影响后续对机组运行状态的评价。

图2 联轴器处振动信号巴特沃斯滤波结果

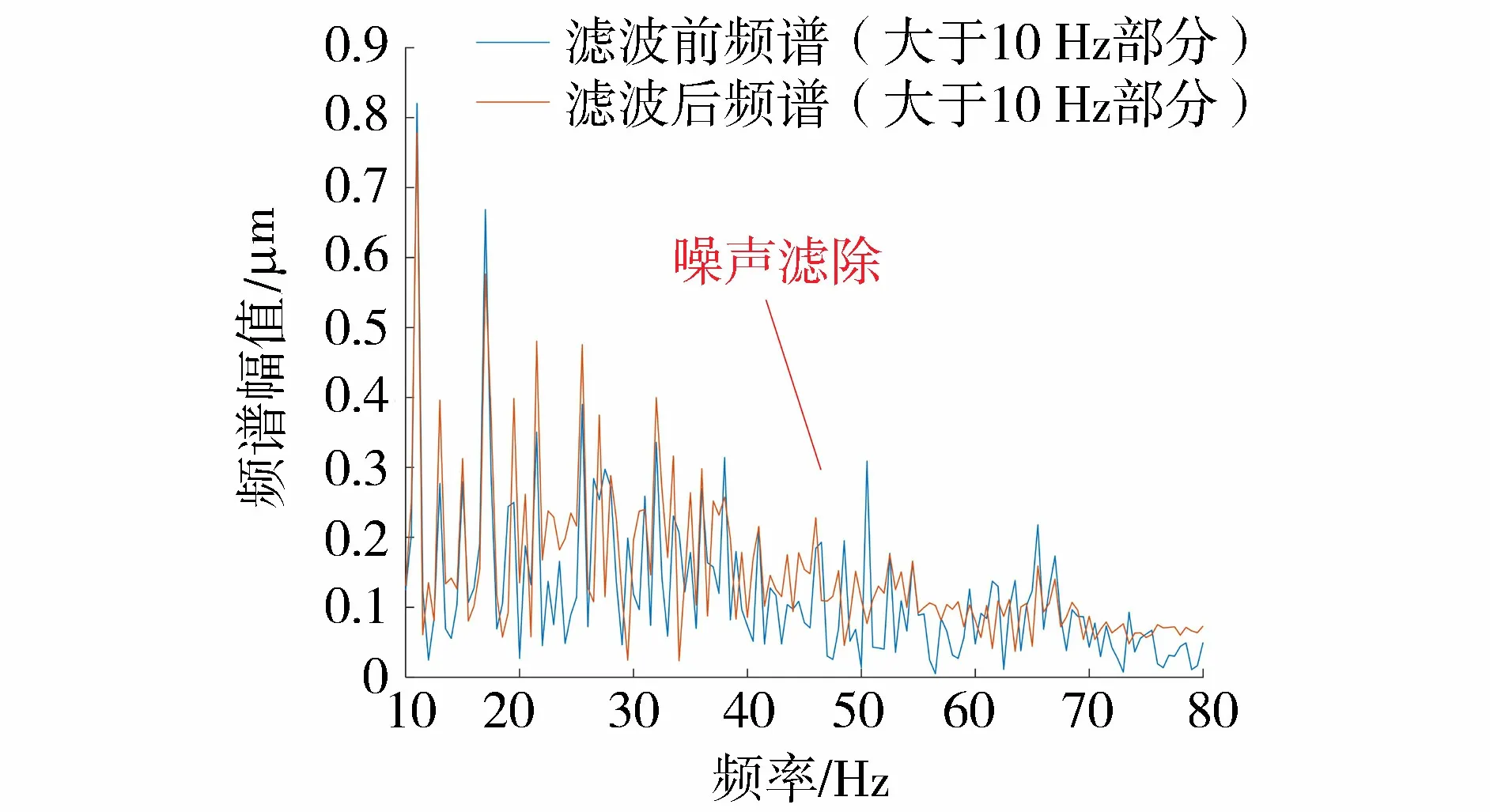
图3 巴特沃斯滤波前后联轴器y方向频谱分析

由图4和图5可知，基于汉宁窗的FIR滤波对40 Hz以上的噪声具有较好的滤除效果，但是和巴特沃斯滤波器类似，同样带来了相位时延。不同的是，基于汉宁窗的FIR滤波造成的延时是线性的，可以通过平移进行补偿。然而，该滤波器的阶数很高，计算量大，不适合实际工程应用。

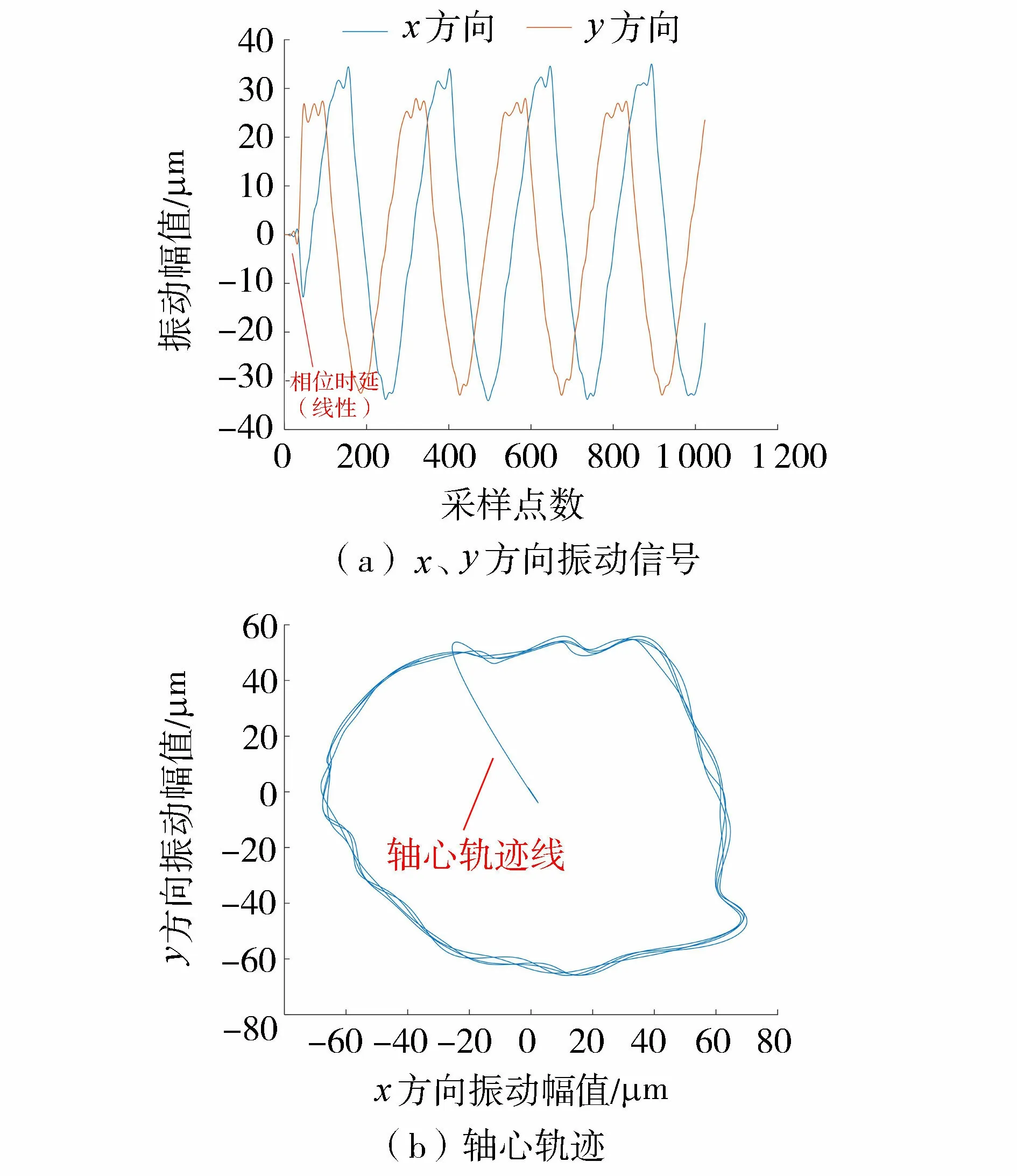
图4 联轴器处振动信号基于汉宁窗的FIR滤波结果

图5 基于汉宁窗的FIR滤波前后联轴器y方向频谱分析

由图6和图7可知，与前2种滤波方法相比，谐波小波频带的滤波效果更好，噪声滤除效果更加明显，x、y方向滤波结果几乎不存在相位延时，无须额外矫正，轴心轨迹也不存在到中心区域的连线。频谱分析可知，谐波小波滤波的过渡带非常窄，几乎能够完全滤除噪声，保留有用信息。因此，基于谐波小波分析的滤波更加适合用来做水泵机组振动信号的预处理。

图6 联轴器处振动信号基于谐波小波滤波结果

图7 基于谐波小波滤波前后联轴器y方向频谱分析

3 结 语

对巴特沃斯滤波器、基于汉宁窗的FIR滤波以及基于谐波小波3种滤波方法对水泵机组实际振动信号滤波结果进行分析，发现二阶巴特沃斯低通滤波以及基于汉宁窗的FIR低通滤波结果中存在滤波前后的时域波形的时延和轴心轨迹的连线。而谐波小波滤波由于过渡带非常窄，相比于另外2种滤波方法滤波效果提升显著，几乎能够完全滤除干扰，且滤波结果中几乎不存在相位延时和轴心轨迹到中心区域的连线。从滤波前后信号的频谱分析来看，对于特定频段的滤波尤其是选定滤波频段范围比较小的时候，谐波小波的滤波优势更加明显。采用基于谐波小波滤波的方法对水泵机组运行振动信号滤波效果更好，有助于准确提取振动信号的特征。