四阶中立型时滞微分方程解的振动性
2022-05-16贾对红
贾对红
(长治学院 数学系,山西 长治 046000)
微分方程的振动性理论在微分方程的定性理论中占有重要的地位,被许多研究学者重视.近年来,高阶微分方程的振动性研究取得了较好的进展,在文献[1-6]的基础上,笔者研究了一类四阶中立型时滞微分方程的振动性,并给出了几个振动准则.

(E)

文中假设下列条件成立:

(A2)c(t)∈C1([t0,∞),R+),b(t)∈C2([t0,∞),R+),h(t)∈C([t0,∞),R+),且
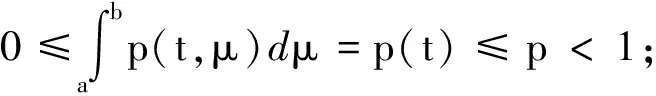
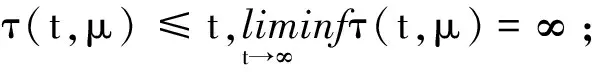
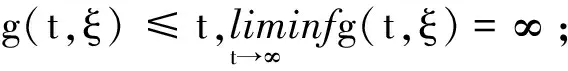
(A6)F(t,ξ,w)∈C([t0,∞)×[c,d]×(0,∞),R+),q(t,ξ)∈C([t0,∞)×[c,d],R+),
设x(t)为方程(E)的一个解,如果x(t)有任意大的零点,则称该解为振动的;否则称为方程(E)的非振动解.若方程(E)的所有解为振动的,称方程(E)是振动的[7].
1 预备知识
引理1 假设A1~A6成立,x(t)是方程(E)的一个正解,则存在充分大的t1>t0,当t>t1时,下面2种情况成立:
(a)z(t)>0,z′(t)<0,(a(t)z′(t))′<0,(b(t)(a(t)z′(t))′)′>0,
(b)z(t)>0,z′(t)>0,(a(t)z′(t))′<0,(b(t)(a(t)z′(t))′)′>0.
证明:设x(t)是方程(E)的一个正解,t∈[t0,∞),则存在充分大的t1>t0,当t>t1时,
x(τ(t,μ))>0,x(g(t,ξ))>0,且
(c(t)(b(t)(a(t)z′(t))′)′)′+h(t)(b(t)(a(t)z′(t))′)′=




当t→∞时,由假设A1知,a(t)z′(t)→-∞.又因(a(t)z′(t))′<0,故存在t4≥t3,当t≥t4≥t3≥t2≥t1时有
a(t)z′(t)≤a(t4)z′(t4)<0,


由假设A1知,当t→∞时,z(t)→-∞,这与z(t)>0矛盾,即证.
引理2若假设A1-A6成立,x(t)是方程(E)的一个正解,z(t)满足情况(a),且
(1)


l-p(t)z(τ(t,a))≥l-p(l+ε)=k(l+ε)>kz(t),

(2)

对上式从[t,∞)积分




2 主要结果
记D={(t,s):t0≤s≤t},D0={(t,s):t0≤s (i)H(t,t)=0,t≥t0;H(t,s)>0,(t,s)∈D0; 定理1假设A1~A6成立,且存在函数H∈X及φ∈C([t0,∞),R)使得 (3) (4) (5) 其中t≥T≥t0,k>1,θ>0, 则方程E的解x(t)或者振动或者当t趋于无穷时趋向于0. 证明:设x(t)是方程E的非振动解,则x(t)为最终正解或负解.设x(t)是最终正解,即设x(t)>0,t≥t1≥t0,则有x(τ(t,μ))>0,(t,μ)∈[t,∞)×[a,b],x(g(t,ξ))>0,(t,ξ)∈[t,∞)×[c,d]. 若z(t)满足情况(b),则 由假设A5,A6得 (c(t)(b(t)(a(t)z′(t))′)′)′+h(t)(b(t)(a(t)z′(t))′)′= (6) (7) 在(7)式两端同时乘以H(t,s)并从[t2,t]积分得 即 由(5)得,当t≥t2时, φ(t)≤w(t), (8) 定理2假设A1-A6及式(1)成立,存在函数H∈X以及R(t)∈C([t0,∞),R)满足 (9) 其中 D(t)=Q(t)-kρ(t)c(t)R2(t), 那么方程E的任何解或者振动或者当t趋于无穷时趋向于0. 上式两边乘以H(t,s),从[t1,t]积分得 这与(9)矛盾. 类似情况(b),可由引理2证得情形(a)的结论,证毕. 因此,此方程的解或者振动或者趋向于0.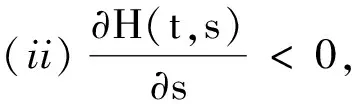

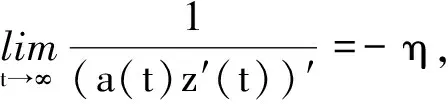










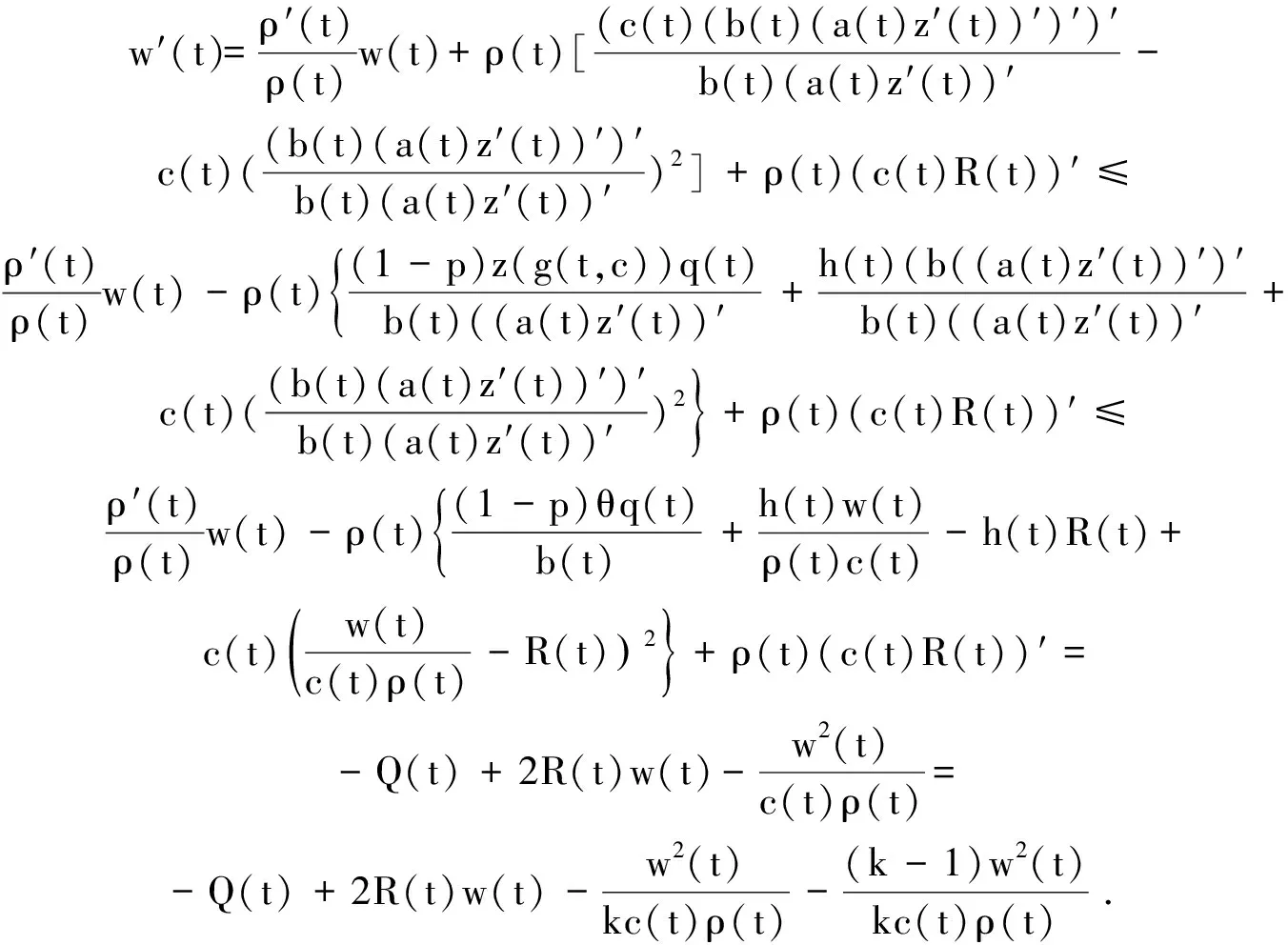


3 应用举例

