一类含参数分数阶q-差分方程边值问题解的存在性

郭彩霞，李华鹏，郭建敏，田海燕

(山西大同大学数学与统计学院，山西大同 037009)

分数阶q-差分理论产生于18 世纪，是研究任意阶次微分特性及应用的理论。作为一种特殊分数阶理论体系，具备了分数阶微积分和离散数学二者的优点。近年来，由于分数阶q-差分微分方程及边值问题在人口增长、量子物理、控制论、经济学、流行病防控等领域的广泛应用，分数阶q-差分方程边值问题解的存在性、唯一性、多解性引起了国内外许多数学工作者的关注。关于带有参数的分数阶q-差分系统也有研究[1-5]。例如李利用Guo-Krasnosel’skii不动点定理、Banach 压缩映像原理、Schauder 不动点定理、Leggett-Williams不动点定理和Scheafer不动点定理详细地讨论了三类含有参数的分数阶q-差分方程边值问题、三类分数阶q-差分方程局部边值问题和两类分数阶q-差分方程非局部边值问题解的存在性[3]。陈通过运用Schauder 不动点定理和Banach 不动点定理讨论了一类具有Caputo 导数的非线性分数阶微分方程边值问题[5]

mild 解存在的几个充分条件，其中Dα，Dβ表示Caputo分数阶导数，1 ＜β＜α≤2，非线性项f∶[0,1]×ℝ →ℝ是连续的，z0,z1∈ℝ。

受到文献[3]和文献[5]的启发，讨论一类带参数的分数阶q-差分边值问题

1 分数阶q-差分基本知识

令q∈(0,1)并做如下定义

定义1设α≥0，f是定义在区间上[ 0,1 ]的一个给定的函数。那么f的Riemann-Liouville 型分数阶q-积分定义为

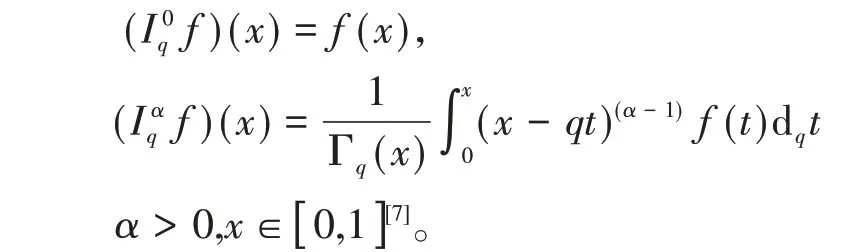
引理2设β∈P+,λ∈(-1,+∝),0≤a＜t≤b,等式成立,

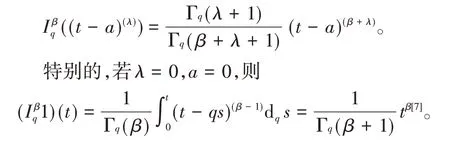
定义2设α≥0，那么函数f的Riemann-Liouville型分数阶q-导数定义为

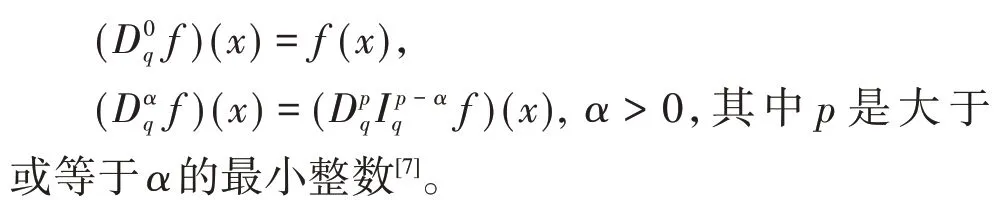
定义3设α≥0，那么函数f的Caputo 型分数阶q-导数定义为

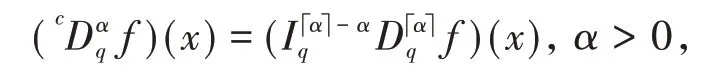
引理3设α∈ℝ+∖N,a＜x,等式成立：

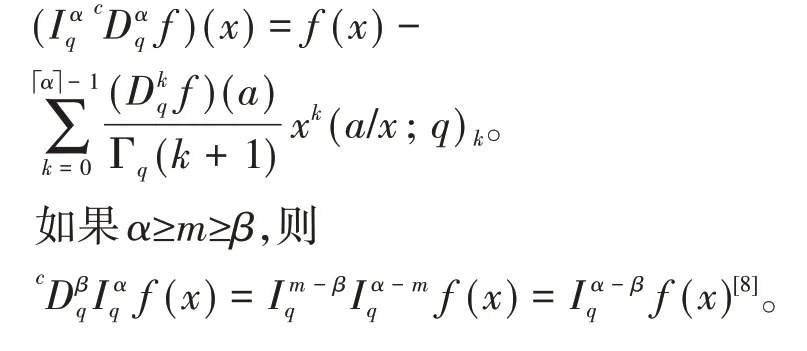
2 等价积分方程的推导

引理4设h∈C[ 0,1 ]是一个给定的函数，3 ＜α≤4，0 ＜μ＜1。那么边值问题

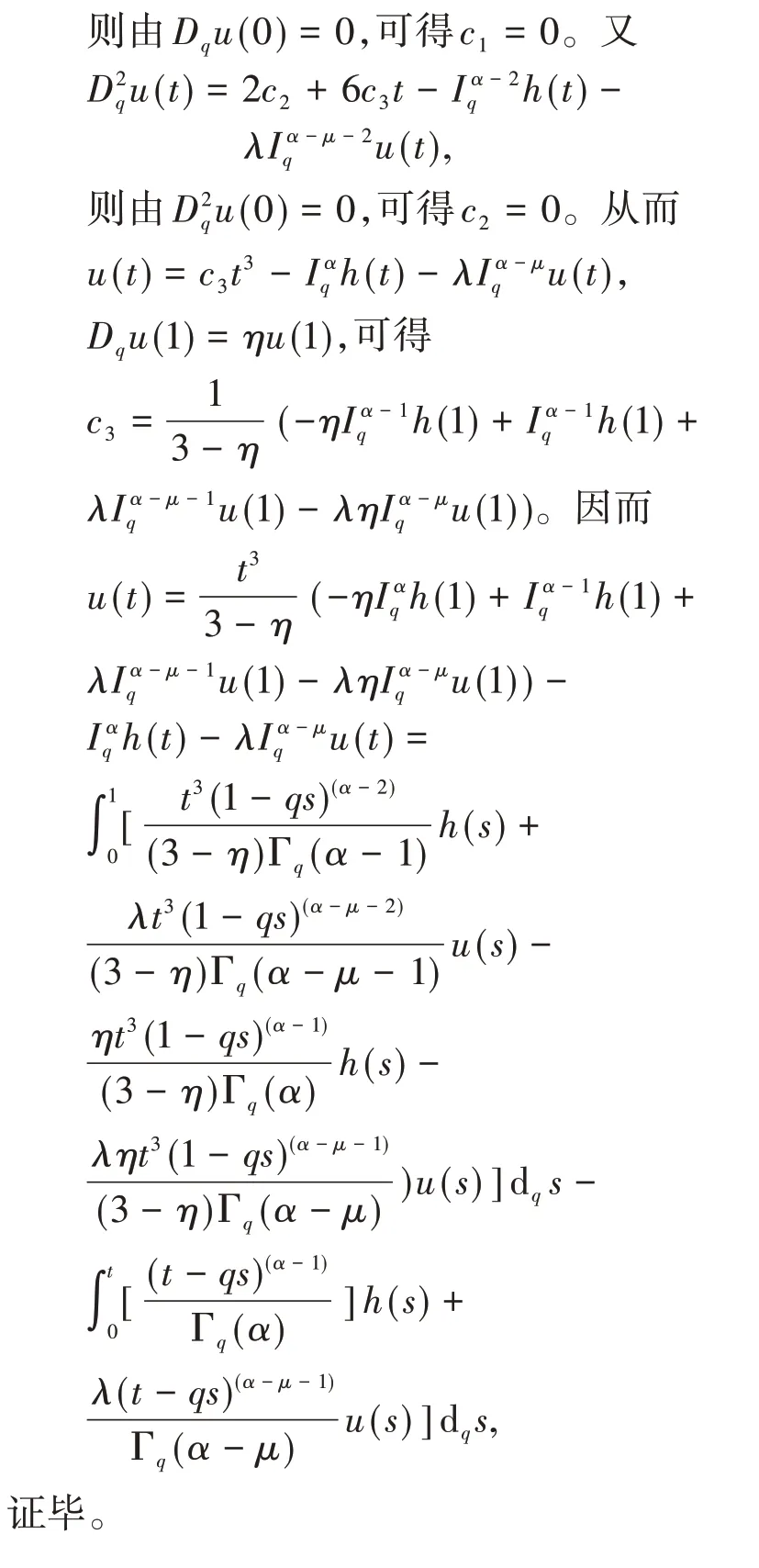
3 主要结论及证明

定义算子为T∶E→E为

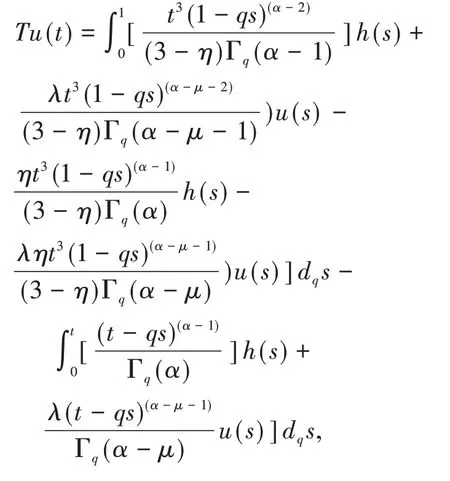
则算子T的不动点等价于边值问题(1)的解。

定义4设E为距离空间，T∶X→X是一个映射，若存在常数θ∶0≤θ＜1使得

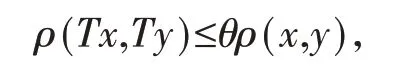
则称T是上x的压缩映射。

定理1(Banach 压缩映射原理) 完备距离空间上的压缩映射具有唯一的不动点。

令E=C([0,1],R)，定义范数为

定理2假设f∶[0,1]×R→R是连续的且存在一个q-可积函数g∶[0,1] →R使得下列条件成立：

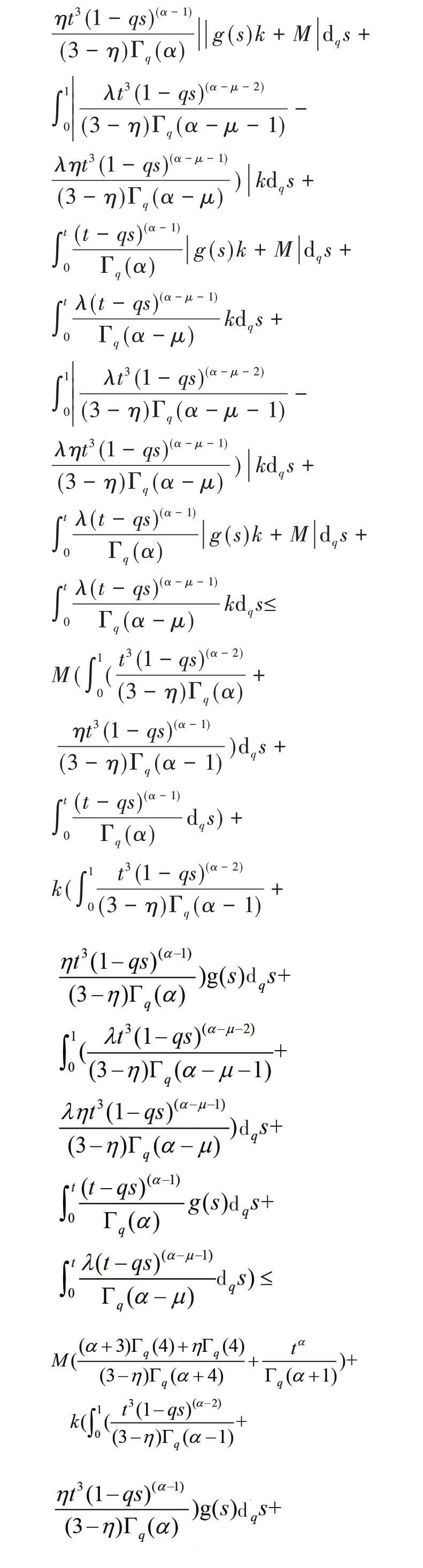
由于p∈(0,1)，故T是E上的压缩映射。故由Banach 压缩映射原理知，问题(1)在E上有唯一的不动点。

讨论了一类分数阶q-差分方程边值问题解的存在唯一性。其中在引理4 中，利用q-导数和q-积分的定义与性质推导了分数阶q-差分边值问题的等价积分方程。在第3 部分中，根据引理4 定义了积分算子，然后定理2通过运用Banach压缩映射原理验证了积分算子是压缩映射，从而得到一类含参数的分数阶q-差分边值问题解的存在唯一性结论。