不确定人口模型的性质

高采文，张志强，卢永红，赵深淼

(山西大同大学数学与统计学院，山西大同 037009)

在人口模型的研究中，微分方程常用来描述人口的动态变化，如1798 年提出的连续Malthus 人口模型[1]为：

其中Pt表示t时刻人口的数量，r表示人口的增长率。

这些模型大多是确定性的，为了解和控制人口的数量及分布，预测人口对外界环境变化的反映，需要建立体现噪声影响的人口动态系统。为此，一些随机人口模型被提出并应用于人口动态行为的研究。但大多数由随机微分方程描述的人口模型，噪声项实际上是一个均值为零，方差趋于无穷的正态随机变量，这意味着人口的瞬时增长率dPt/dt在每一时刻都有无穷大的方差。在实际中，这是不可能的。因此，用随机微分方程来模拟人口的动态变化也不尽合理。

不确定人口模型是由Liu 过程驱动的微分方程。不确定理论是刘宝碇[3]于2007年提出的，是数学的一个分支，用来模拟人类的不确定性。2008 年不确定过程被引入，被用来描述随时间变化的不确定现象，不确定微分方程就是由不确定过程驱动的微分方程。Liu 过程是具有Lipchitz 连续样本轨道的稳定独立增量过程，在不确定性分析中起着基础性的作用。近几年，不确定微分方程已经成为处理动态不确定系统的主要工具，已经广泛应用在金融、工程技术、物理、医学等领域[4-6]。

1 模型的解

设0 ＜α＜1，由Yao-Chen 公式[3]，不确定人口模型dPt=rPtdt+σ1PtdCt具有轨道：

由于T+和T-是不相交的集合，Ct是一个独立增量过程，所以有

由于T+和T-是不相交的集合，Ct是一个独立增量过程，所以有

定理2设Pt为不确定人口模型(2)的解，Pt有逆不确定分布：

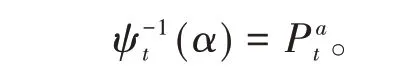
证明对于任意的S，由于

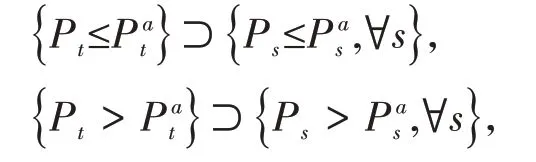
根据不确定测度的单调性,有

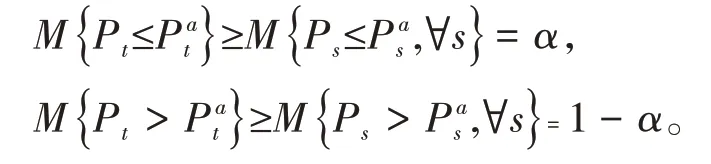
由不确定测度的对偶性，

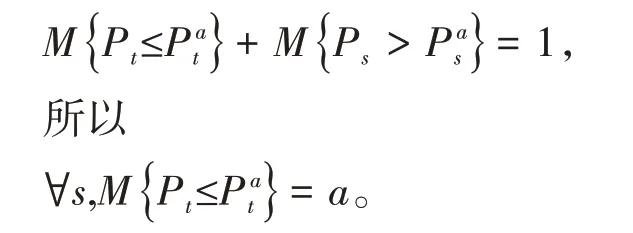
也就是说，Pt有逆不确定分布。

例1考虑不确定人口模型(2)，其中r=0.02，σ=1，P0=3.9 × 106。该模型的解为：

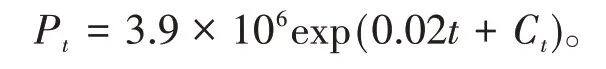
Pt的逆不确定分布在t=1/2，如图1所示。

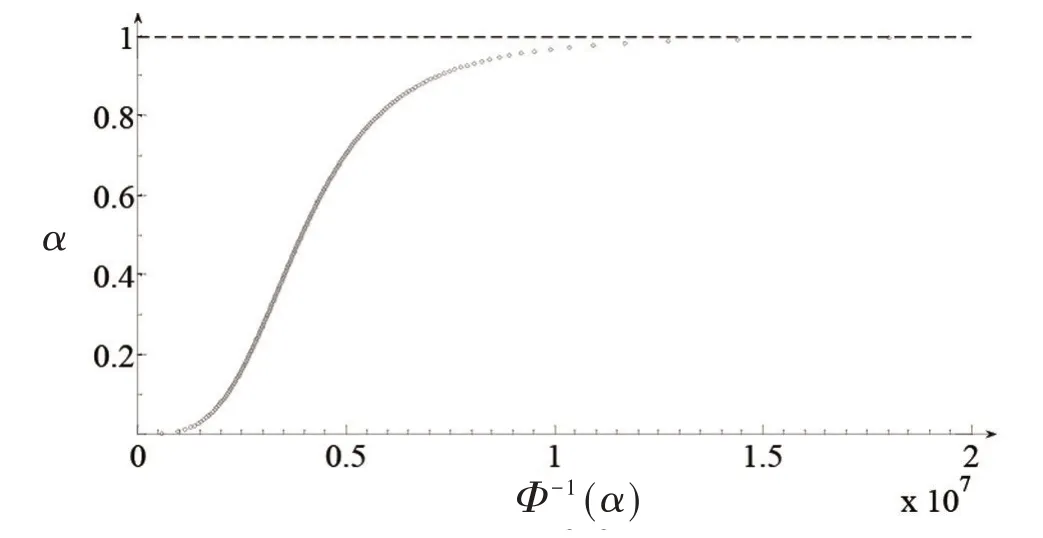
图1 解的逆不确定分布

例2考虑不确定人口模型(2),其中r=0.02,σ=1,对于给定初值P0=390,模型有α轨道：

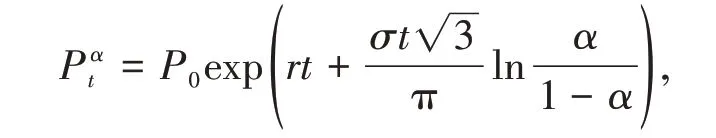
如图2所示。

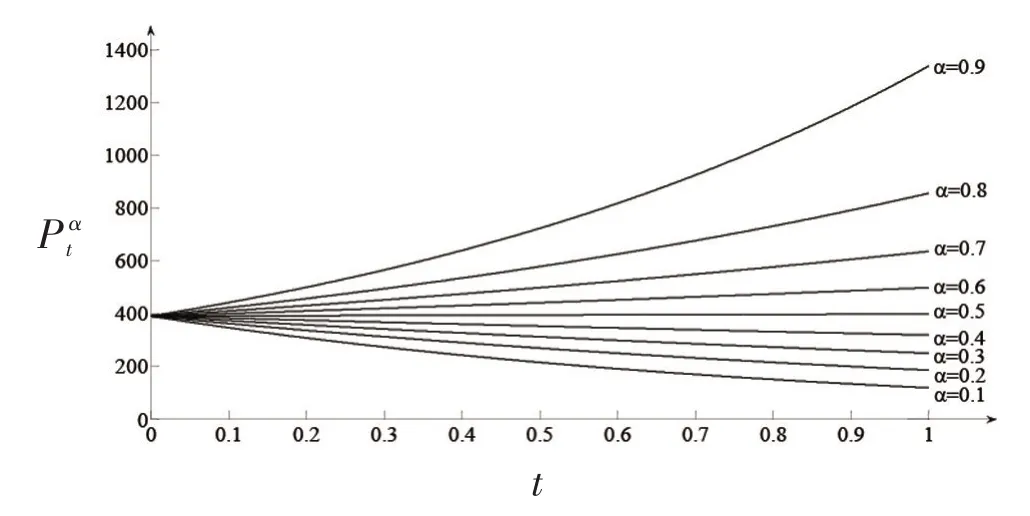
图2 不确定人口模型的α轨道

2 模型的稳定性

如果模型是稳定的，意味着初值的微小扰动不会导致解的性态产生有影响的偏移。目前，不确定微分方程的稳定性主要有6 种类型，即测度稳定、均值稳定、p阶矩稳定、逆分布稳定、指数稳定和几乎处处稳定。文献[7]给出了不确定微分方程在t≥0 时，依p阶矩稳定的定义。

根据定义，可以证明不确定人口模型(2)在t≥0 时依p阶矩不稳定。但是，实际中，模型经常应用在t为有限数时，所以给出t在有限区间上时，不确定微分方程p依阶矩稳定的定义。

定义1设T为有限正数，t∈[0,T]，Xt和Yt为不确定微分方程

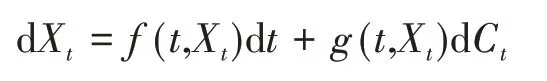
的任意两个解，X0和Y0为初值。如果满足

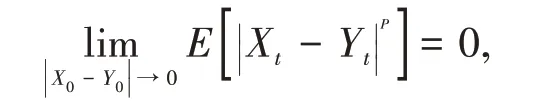
0 ＜p＜+∞则称这个不确定微分方程依p阶矩稳定。

定理3设T为有限正数，t∈[0,T]，不确定人口模型(2)在[0,T]上依p阶矩稳定。

证明对给定的初值X0和Y0，令

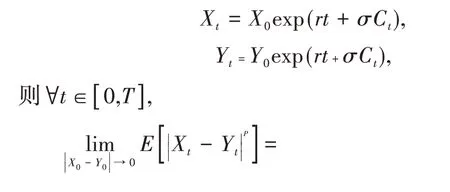
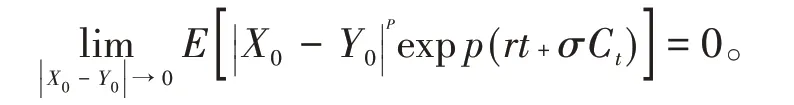
由定义1，模型(2)在[0,T]上依p阶矩稳定，定理证毕。

3 结论

在人口模型的研究中，微分方程作为一个有力的数学工具已经得到广泛应用，取得了丰硕成果。用微分方程描述的人口模型大多数是确定型或随机型，这些模型没有把不确定性因素考虑进去，但是在现实中，人口变化必然会受到各种不确定性因素的影响。如果用随机微分方程来描述，一方面变化并非是在稳定环境下的随机变化，另一方面随机微分方程的噪声项实质上是一个均值为零，方差为无穷大的正态随机变量，这两方面的原因表明用随机微分方程来描述人口变化也有不尽合理之处。基于此，考虑到自然界中，出生率和死亡率都具有不确定性，不受不确定噪声扰动的生物种群是不存在的，不确定人口模型更符合生物种群变化的趋势。

研究了由不确定微分方程刻画的不确定人口模型的性质，文中得出模型的α轨道和解的逆不确定分布，并讨论了有限区间上模型的P阶矩稳定性。在今后的研究中,可以建立环境容纳率被不确定因素扰动的人口模型，或者利用带跳的不确定微分方程建立带跳不确定人口模型，这些都是值得研究的方向。