近邻场优化算法研究与应用综述
2022-05-15张洪瑞张海军
伍 洲,张洪瑞,张海军,宋 晴
1.重庆大学 自动化学院,重庆400044
2.哈尔滨工业大学(深圳)计算机科学与技术学院,广东 深圳518055
3.北京邮电大学 人工智能学院,北京100876
随着信息科学技术的迅猛发展,人们发现传统方法已很难高效准确地处理一些实际高维、多峰值的复杂问题。研究者们受自然界中生物行为的启发并提出群体智能优化算法[1-2],为上述问题提供了一种高效的解决方案。群体智能优化算法通常具有较好的鲁棒性和跳出局部最优的能力,以粒子群优化算法(PSO)[3]、蚁群算法(ACO)[4]、人工蜂群算法(ABCA)[5]等为代表的群体智能优化算法以及相关的改进算法[6-8]已广泛应用于实际工程领域解决优化问题。
Wu等人受自然界中生物个体向邻居交流和学习行为的启发,于2012年提出近邻场优化算法(简称近邻场算法,NFO)[9-10]。NFO 算法提出了近邻场模型,模仿了自然界中生物个体向优质邻居靠近而疏远劣质邻居的局部协作特征,形成了一种独特的局部搜索机制。近年来,研究者们对智能优化算法研究呈爆炸式增长,每年都有众多的新型优化算法及其相关改进算法被提出,因此,对现有一些经典算法的综述工作是具有价值和意义的。目前,一些经典的群体智能优化算法如PSO、ACO、遗传算法(GA)等已有较详细的综述文献[11-13],而NFO算法自2012 年提出以来,以其参数较少、收敛速度快、鲁棒性高等优势受到国内外学者广泛关注和研究,但至今却并没有较为完整的综述性文献对算法的改进以及应用研究进行梳理和总结。本文将对NFO算法近10年来的改进和应用研究进行综述,以期对NFO 算法未来的扩展研究提供一定的参考价值。
1 近邻场算法
近邻场算法的搜索机制依靠个体受邻居影响移动,优质邻居会产生吸引力,劣质邻居产生排斥力,个体在两种作用力下会朝着靠近优质邻居而远离劣质邻居的方向移动。在最小值优化问题中,标准算法的寻优步骤如下:
(1)初始化NFO 参数,包括种群大小N、最大迭代次数G、学习率a、突变概率Cr;初始化种群,在给定的搜索范围中随机生成初始解。
(2)定位。找到每一位个体的优质邻居xci与劣质邻居xwi,其公式如下:
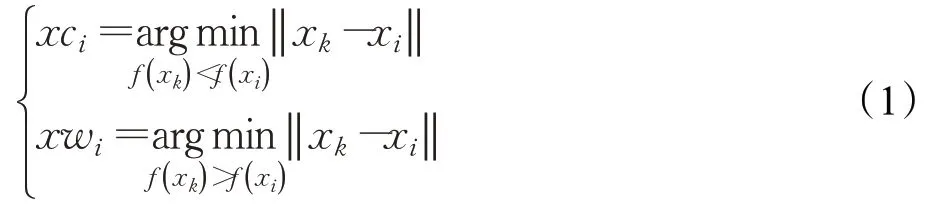
其中,xk表示满足适应度函数关系f(xk)<f(xi)或f(xk)>f(xi)的个体集合,‖xk-xi‖表示两个体间欧式距离。
(3)变异,得到变异个体vi,公式如下:
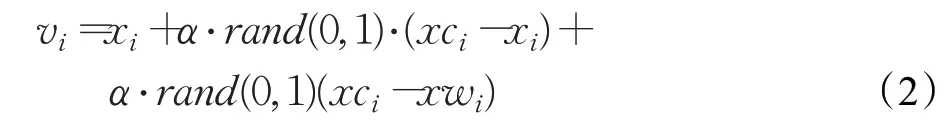
(4)交叉。变异个体与原个体交叉重组得到交叉个体ui,公式如下:
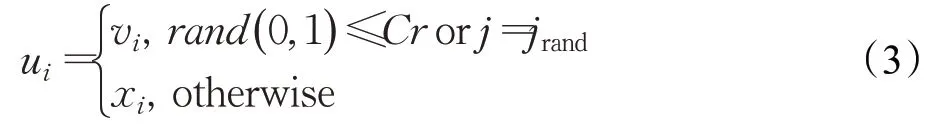
其中,参数j表示当前个体的维度,jrand表示区间[0,j]某随机维度。
(5)选择。在ui、xi中选择更优适应度值的个体,公式如下:
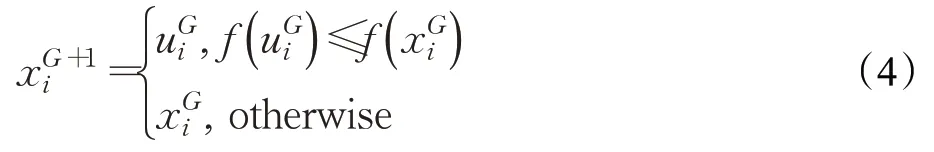
(6)检查是否满足算法停止标准。重复步骤(3)至(5),直至满足停止标准。
算法的近邻寻优机制依靠个体近邻,虽然具有参数少、计算量小等优势,但算法全局搜索能力较低,存在易陷入局部极值以及早熟收敛等问题,如图1。

图1 NFO算法流程图Fig.1 Algorithm flow chart of NFO
2 算法改进研究
虽然近邻场算法在许多领域的优化问题中都表现出了较好的优化性能,但算法仍然存在易陷入局部最优、鲁棒性不高以及早熟收敛等问题。为进一步提高算法优化性能,扩展算法应用领域,研究者们对标准NFO算法进行了相关研究改进,提出了许多拥有更强优化性能的改进算法,例如用于求解离散问题的二进制NFO算法、整数型NFO算法;改进算法搜索步长以及提升种群多样性的结构化NFO算法、树结构NFO算法,用于求解多目标问题的多目标NFO算法等。下面详细介绍相关NFO改进算法。
2.1 混合算法
Zhang 等人将AdaBoost 算法与NFO 结合提出自适应增强NFO 算法(ABNFO)[14]。ABNFO 算法借鉴了AdaBoost算法组合弱求解器构建强求解器的思想,通过组合三种弱求解器用来搜索全局最优。ABNFO算法的循环由三种搜索机制组成,分别为利用性搜索、普通搜索以及探测性搜索,其数学函数形式如下所示:
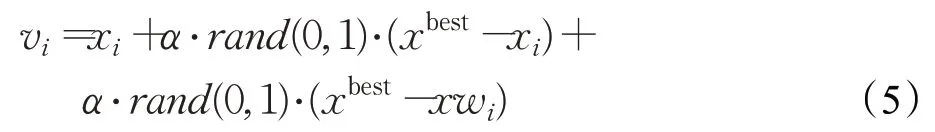
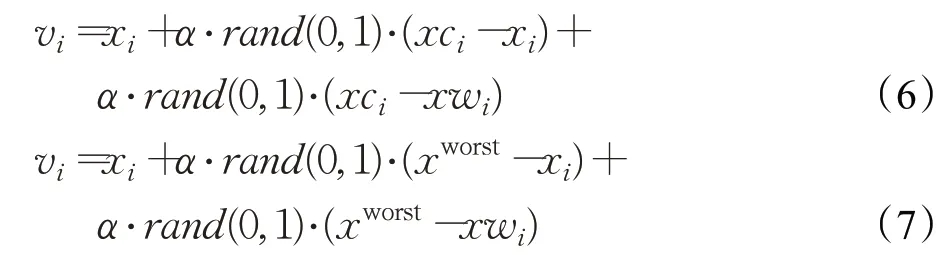
式中,xbest与xwrost分别表示当前全局最优和最劣个体。相较原算法而言,ABNFO算法的搜索方式更灵活、搜索范围更广,从而使算法具有更强的跳出局部最优的性能,算法引入了精英个体结合近邻搜索的方式扩大算法搜索步长,但复杂的组合搜索机制较大程度增加了算法计算的时间复杂度,并且算法更易受初始种群的结构和质量影响,导致鲁棒性不高。实验对比了ABNFO、NFO 算法以及二分法在非蜂窝物联网资源分配问题中的优化性能,结果表明在使用ABNFO 算法时系统具有更高的能源效率,并且ABNFO算法具有更高的收敛性。
为提高算法在复杂数值优化问题中的求解效率,Wang等将三角变异策略、NFO近邻场优化机制与DE算法结合提出改进算法(NFO-DE)[15]。作者结合NFO 邻域搜索机制与三角变异策略,定义了一种结合邻居搜索的组合变异策略,具体如下:
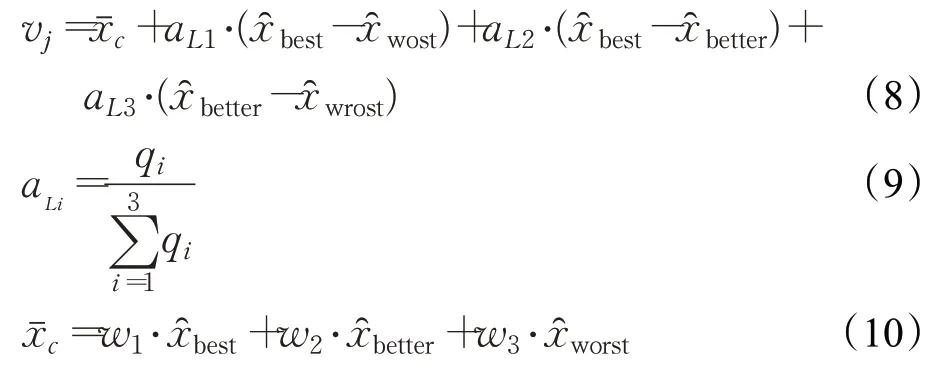
式中,a代表学习率,其中参数q1=1,q2=rand(0.75,1)以及q3=rand(0.5,q2),为凸组合向量,参数wi取值方式与计算方式均与a相同,为目标个体邻域内随机选择的3 个候选解。为提升算法的收敛速度,增加了选择机制如式(11)所示:

其中,G代表种群当前迭代次数,GEN代表最大迭代次数。当式(11)条件满足时,算法会以组合变异策略的搜索机制迭代,否则采用原算法的搜索机制。结合三角变异策略的近邻搜索机制从个体附近邻域随机选择近邻个体,在一定程度上增强了算法的搜索步长和搜索随机性,但复杂的搜索方式降低了算法的收敛速度,虽然通过引入概率选择机制提升算法计算速度,但会导致算法鲁棒性不高,可以在算法不同时期采用不同搜索策略,在算法后期使用随机性更高的搜索机制避免陷入局部极值,而在前期使用收敛速度较快的近邻搜索等策略。在解决自抗扰控制器的参数优化问题中,作者通过对比自抗扰控制器参数与系统鲁棒优化的性能,验证了NFO-DE算法处理复杂参数优化问题的有效性,但文献并没有对算法的对比实验以及基准函数的测试实验。
Wang等人将二进制NFO算法(BNFO)的离散优化思想与DE算法结合提出改进算法(BNFO-DE),用于解决建筑节能改造中的非线性整数优化问题[16],实验对比了BNFO-DE 算法与BNFO 算法在该问题上的优化性能,实验结果表明BNFO-DE算法具有更强的收敛精度,但缺少其他基准函数的测试实验。
针对高效全局优化算法(EGO)[17]处理黑箱函数极值问题时所存在的局部搜索能力较差的问题,Yu等人将NFO近邻搜索机制与EGO结合提出改进算法(NFSEGO)[18]。NFSEGO算法在原始EGO算法步骤中添加了NFO算法的近邻定位、选择以及变异操作,使用近邻搜索机制弥补了EGO 算法局部搜索能力不足的缺陷,使算法具有更强的优化性能,使用了5组基准函数以及天线优化设计应用实验测试算法性能,实验结果表明改进算法的收敛精度和效率都优于原算法。
以上改进通过结合其他算法搜索机制提升算法优化性能,包括引入三角变异替换近邻定位的局部搜索策略,引入精英个体并使用组合搜索的形式增加个体搜索的随机性,初代种群的全局预处理等改进方式。除此以外,也可以考虑结合其他更多优秀算法的寻优机制对算法进行改进。例如,可以借鉴人工蜂群算法(ABC)的蜂群结构对算法初代种群进行改进,但需要注意算法后续近邻定位计算的复杂度和计算量,引入粒子群算法、灰狼算法(GWO)等的精英策略改进近邻场搜索机制,提升算法全局搜索性能,结合蚁群算法(ACO)中蚂蚁状态的概率更新机制,或者借鉴遗传算法(GA)中交叉、变异算子的改进策略以提高算法的种群多样性。
2.2 搜索能力
NFO算法寻优过程中,个体仅依靠相邻最近的两个邻居个体,而非当前种群最优个体,这种局部搜索机制使得个体们具有不同的搜索方向,从而增加了算法的种群多样性。但当初始种群结构复杂或较大种群数量时,由于算法的全局搜索能力不强,算法的收敛性能不高,且更容易陷入局部极值。因此,为提高算法的全局搜索性能,需要对近邻场局部搜索机制进行改进,可以在定位中通过二次搜索近邻的策略,此外,也可以通过调整参数和搜索步长方式改进。具体改进策略如下。
Ao等人为提高NFO算法的全局搜索能力以及种群多样性,提出结构化NFO 算法(NFO-n)[19]。定义个体NFO-n,NFO-n在迭代搜索近邻时可以根据参数n调整搜索步长搜索距离第n近的邻居从而提高算法全局搜索能力。使用了7种测试函数对算法进行测试,实验表明NFO-n算法在与粒子群优化算法(PSO)、自适应差分进化算法(SADE)[20]等其他四种算法相比具有相当的优化性能,并且NFO-n更适合解决多模态优化问题。针对标准NFO 算法的简单连接网络结构容易陷入局部最优、早熟收敛等问题,Ao 等人提出树结构NFO 算法(DNFO)[21],算法引入树形连接结构以增强算法鲁棒性。DNFO 算法调整了算法搜索步长以增强算法全局搜索能力以及种群多样性。使用类似树状结构的近邻搜索方式增广了近邻搜索范围,提升了种群结构的多样性。使用了CEC2014测试集等30种基准函数对算法性能进行测试,实验结果表明算法具有比NFO 算法更好的优化性能。但当搜索步长增加到3以上时,算法的优化结果并无明显提升,仍存在继续研究和改进的空间。
以上改进方式实质都是通过改进算法的近邻定位机制来增加个体与最近邻的距离,从而提升算法的搜索步长。但当搜索步长较大时,算法的多次近邻搜索会增加算法计算的时间复杂度,降低算法优化性能。除此以外,可以考虑借鉴Adam(a method for stochastic optimization)优化算法[22]思想实现算法搜索步长的自适应调节,或者引入概率常数来反馈步长信息以及精英个体信息共享等机制改进算法搜索性能。
2.3 编码方式
标准NFO算法所采用的实数编码方式使得算法难以解决实际离散优化问题,针对此问题,研究者们通过改变个体的编码方式提出了二进制NFO与整数NFO算法,具体如下。
Wu等人提出二进制NFO算法(BNFO)[23]。BNFO中的个体由二进制编码位串组成,由于编码方式不同,算法在定位步骤中的欧式距离更改为汉明距离,BNFO将标准NFO算法中的实值个体重新编码为二进制位串个体,在离散优化问题中BNFO优化性能更好,且维持了原算法的收敛精度以及鲁棒性,但收敛速度较慢。Zhang等人提出整数NFO算法(INFO)在解决实际离散优化问题中表现良好[24]。INFO通过两个映射函数实现实值个体与整数个体的转换,种群在每次迭代之前把整数值个体转换为实数值个体,并在变异步骤之后再把实值个体转换为整数个体。算法通过迭代前后对个体值转换使得算法能够优化离散问题,并且收敛速度快于BNFO算法。
上述改进借鉴二进制粒子群算法中种群个体二进制编码串离散化表示的思想,但增加了算法整体计算量和复杂度。除此以外,可以考虑引入Sigmoid 函数以及其他概率模型等来生成二进制解,也可以将种群搜索空间进行改进,通过引入布尔点阵等特征选择策略来解决离散优化问题,但也需注意算法的计算时间复杂度问题。
2.4 多目标NFO算法
标准NFO 算法常用于解决连续单目标优化问题,为解决多目标优化问题,Wu 等人同年又提出了多目标NFO 算法(MONFO)[25],MONFO 算法的流程与NFO 类似,不同之处有以下几点:
(1)在定位步骤中,MONFO 融合了CGO 算法根据个体适应值分层的策略[26],在多目标优化中,MONFO会随机选择某一目标并根据种群个体的适应值大小对个体排序,均分成n个层级。并在此基础上重新定义算法的定位步骤如下:
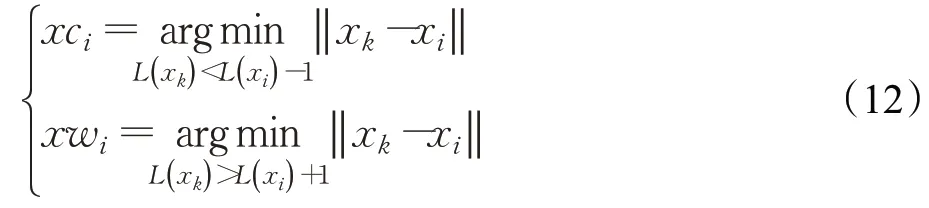
其中,L(x)表示个体x所在层级。
(2)在选择步骤中,作者定义了广泛支配概念代替传统多目标算法所使用的帕累托(Pareto)支配,MONFO的选择步骤如下所示:
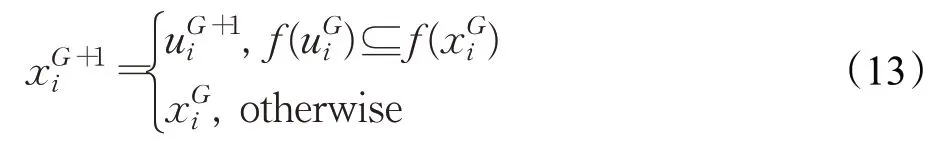
其中,⊆表示广泛支配关系,定义如下:
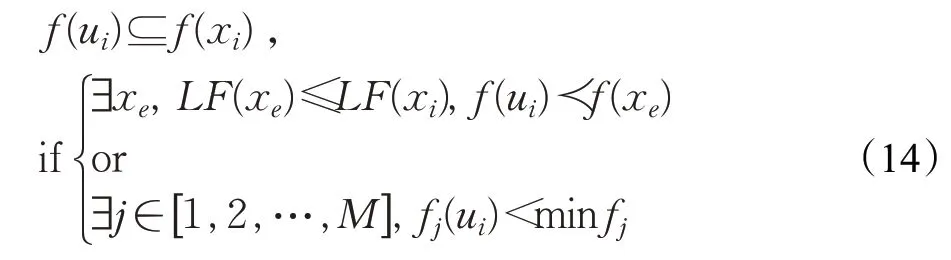
式(19)中,≺表示传统Pareto 支配,LF(xi)为个体所在层级。其中广泛支配定义为:个体ui若能广泛支配xi,当且仅当个体ui至少有一个目标函数值小于该目标函数的当前最小值或ui能够Pareto支配xi所在层级及其以下层级的任意个体xe。除此以外,在算法下一次迭代之前,会将当前种群的非支配解加入外部存档中,若存档中解的个数大于种群数量,根据密度估计进行修剪。前N个稀疏解继续到步骤2,直到满足停止准则。
MONFO 算法作为一种依靠邻域协作的局部搜索算法,在12 种测试函数中的优化效果能够与SPEA2、MOPSO以及GED3等全局多目标搜索算法[27-29]媲美,并且对于一些高维目标的多封函数,MONFO算法的准确性以及候选解的多样性更优。
Wang等人设计了由单目标引导的多目标优化框架(SOGMO)用于求解多目标优化问题,引入NFO向邻居学习的优化策略,提出结合SOGMO 框架的改进算法SOGMO-NFO[30-31]。该框架利用传统单目标优化方法解决多目标优化问题(MOPs),仿真实验采用了13种基准函数比较算法与传统多目标进化算法(MOEAs)[32]的优化性能,测试结果表明算法在收敛性和多样性上都优于MOEAs算法,但目前算法并没有应用于实际优化问题中。
2.5 参数控制
NFO 算法是根据学习率a这一重要参数同时控制个体朝优质或劣质邻居的搜索范围,学习率的不同取值会较大程度地影响算法的进化方向和优化性能。若a取值较大,导致算法的搜索步长过大而跳过种群最优导致早熟收敛;若a取值较小,则会增加算法搜索的次数导致收敛速度下降,此外,突变概率Cr也会影响算法的搜索速度。
Zhang等人将引入集成学习策略来控制算法参数[33]。创建了三组包含NFO 常用参数的串行组合,算法初始采用组合中的随机一种组合开始迭代,并根据迭代过程个体的适应度值进行参数更新,参数更新规则如下:
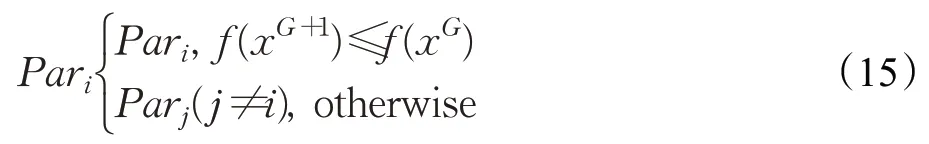
其中,参数Par表示数组中的参数组合,下标i,j表示参数在组合中的索引值。算法在迭代中通过适应度值比较选择出优化性能最好的参数组合,从而在一定程度上提升算法的参数自适应性。使用了两种基准函数对改进算法进行测试,实验结果表明改进算法的收敛速度明显快于固定参数值的NFO算法,并与GA等三种其他进化算法进行了比较,证明改进后算法在两种测试函数下的收敛速度均优于GA,与梯度下降法以及牛顿法相比,算法前期收敛速度慢但后期更快。
上述改进方法通过在算法迭代前预设参数组合的形式在一定程度上提高算法参数自适应性,但增加了算法的复杂度和计算量。除此以外,可以考虑采用不同学习率分别控制个体对优质和劣质邻居的搜索范围,通过迭代次数以及种群个体适应值的动态自适应性调整参数值的方式改进,还可以通过引入变形函数等动态控制参数,使算法在不同搜索时期拥有不同的搜索范围,从而提高算法收敛速度和精度。
2.6 算法改进小结
改进算法汇总如表1 所示,包含了混合算法、搜索能力以及编码方式的相关改进算法。相较于其他一些新型优化算法如天牛须搜索算法、花授粉算法等[34-35],NFO 算法现有的改进研究内容总体而言还比较欠缺。例如在混合算法改进中,现有改进算法如ABNFO、NFSEGO等算法都是通过结合NFO算法的局部搜索机制,从而提高算法的全局搜索能力以增强算法优化性能,除此以外还借鉴其他一些局部搜索算法来改进算法的搜索机制,或者引入混沌概念和随机策略等。NF0-n及DNFO算法通过调整近邻搜索步长,增强种群多样性的方式使算法跳出局部最优能力增强,但此类方法应注意在搜索步长较长时会增加算法的计算复杂度,影响算法的收敛效率。NFO算法的参数较少,但参数的敏感度较高,就目前来看,关于算法参数的改进算法较少,现有的NFOEnsemble 算法只是通过外部建立参数组合的方式来提升算法的参数自适应性,对算法本身的搜索机制并没有做出改进。
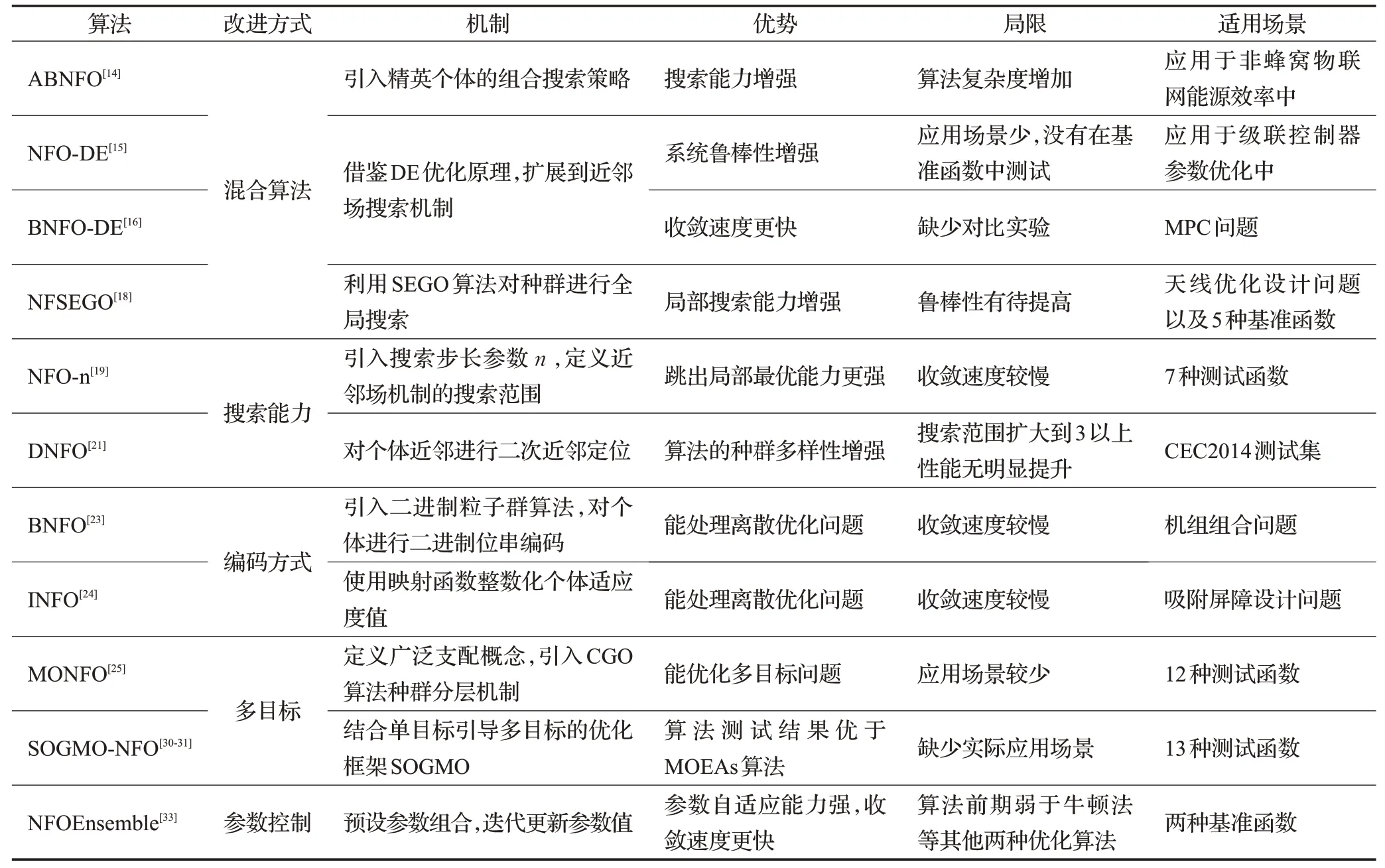
表1 算法改进研究汇总Table 1 Summary of improved algorithm research
3 算法应用
3.1 智能建造及能源效率
文献[14]中Zhang 等人为提高物联网传输能源效率,使用ABNFO 算法提高无蜂窝结构物联网模型的能源效率,建立基于功率控制的能源效率优化模型,优化无蜂窝物联网的资源分配以及数据传输问题,保证了数据传输质量。并通过传输功率、电路功率、设备数量等。仿真测试了算法性能,测试结果表明ABNFO 算法在小功率的优化效果优于NFO 算法,大功率时效果相当;并且ABNFO 算法在多台设备情况下对能源效率的优化效果更强。
文献[16]将维修计划优化问题(MPO)建模为最优控制问题并引入MPC控制器模型,建立基于BNFO-DE算法的数值求解器用以求解该动态规划问题中的非线性整数优化问题。实验以小型建筑节能改造工程为例,验证了该方法的有效性,并与传统BNFO、DE算法进行比较,结果表明BNFO-DE算法的收敛性和精度更高。
Wu等人使用MONFO算法以优化建筑节能改造问题。从改造成本、节能、净现值三方面将建筑节能改造问题建模为多目标优化问题,并使用MONFO 优化求解[36]。案例测试结果表明MONFO 算法能找到帕累托最优方案,且方案在可行区间具有分布多样化的优势。文献[33]中,Zhang 等人将改进算法用于优化无蜂窝结构MIMO 网络的功率控制、频谱效率,仿真实验证明了算法在具有多种传感器的MIMO网络中优化的有效性。
3.2 路径规划
Ao 等人将NFO 算法用于钢筋排布问题[37],对三种类型(T型、+型和L型)梁柱节点中的钢筋排布问题进行优化,实验结果表明在T 型以及+型梁柱节点的钢筋排布优化中,NFO算法具有比PSO、DE算法更短的收敛时间,并且三种算法的优化结果大致相当。
Xu等人将NFO算法应用于建筑领域中的砌体墙排布问题[38],文献针对现有仅依靠工人的先验知识或者使用人工建筑信息建模(BIM)模型技术具有的易出错,效率低等缺陷,提出了一个基于BIM的砌体墙自动化设计框架并对实际应用场景下的砖块布局问题建模为智能优化问题,采用NFO、PSO、DE 算法分别对该优化问题进行求解,验证了该框架的有效性,实验结果表明NFO算法具有比PSO、DE更短的计算时间,并且优化布局所需的砌体墙砖块更少。
3.3 组合优化与经济调度
为降低机组组合问题(UCP)的成本,文献[23]先使用BNFO算法处理UCP问题中的单元调度问题,再通过Lambda 迭代方法解决经济负荷调度问题,并循环步骤至满足停止条件。经实验测试,BNFO算法具有比遗传算法(GA)[39]、粒子群算法(PSO)等更低的优化成本和收敛时间,且更适合大规模的UCPs问题优化。
Zhu 等人为降低智能电网的总体成本并提升用电效率,提出一种半张量积求解控制网络演化博弈框架下智能电网需求侧管理的方案[40],并将方案建模为非线性二元优化问题,使用BNFO算法进行优化求解。仿真实验证明了方案可行性,实验结果表明BNFO算法能够优化控制网络演化博弈框架下系统的瞬态性能。
3.4 其他应用
为解决超声速飞行器飞行中受外部干扰以及参数不确定性问题,文献[15]提出NFO-DE 算法。通过设计级联式ADRC控制器模型,并使用算法对该控制器的参数进行随机鲁棒优化,实验表明参数优化之后的系统控制鲁棒性得到提高。文献[24]将NFO 算法及改进算法BNFO、INFO 用于优化非线性吸附屏障设计问题,并与GA 算法及其变种算法进行比较分析,仿真实验表明NFO 改进算法具有更快的收敛速度并且INFO 算法的优化效果显著。为解决机器人动态模式识别问题,Chen等人将NFO 算法应用于2-DOF 下肢外骨骼模式识别中[41],实验测试,NFO 相比PSO、GA 的适应度优化曲线具有更高的精度和优化性能。Zhang 等人针对移动无线传感器网络模型(MWSN)寿命较短等问题,提出一种可以延长MWSN 寿命的系统模型[42],并使用NFO、GA等5 种进化算法求解,通过对实验结果的讨论和分析,为EC 算法解决MWSN 寿命问题提供了一种可行建议。Zhang 等人基于对角加载技术提出一种自适应信号方向预测方法[43],为解决方向不准确信号时声波束形成鲁棒性较低的问题,同时增强期望信号、抑制干扰和噪声,利用NFO 算法实现对角加载方法中阈值的自适应控制。仿真结果表明优化后系统信噪比提高。
4 总结与展望
近邻场算法自2012 年提出以来,因其较好的优化性能以及参数少、收敛速度快等优点,引起了相关领域众多研究者们的关注与研究。但就目前来看,算法的改进和应用研究依然不够深入和广泛,仍然具有进一步研究和改进的空间,NFO算法未来的研究重点可以考虑放在以下几个方面:
(1)NFO 算法的理论研究。NFO 算法的寻优思想源于PSO和GA等经典进化算法,但相比之下算法的提出时间不长,现有的理论研究相对较少。NFO算法需要调节的参数仅有学习率a和变异率Cr,但参数敏感度较高,调节算法参数能够一定程度上提升算法的全局搜索能力从而避免陷入局部最优,但目前有关算法参数的理论分析还明显不足,其中学习率a的取值对算法性能影响较大,可以对算法参数在不同类型优化问题中的最优参数值以及取值范围进行分析,有利于参数的自适应改进和平衡算法的全局搜索和局部搜索,突变概率Cr对算法的收敛速度产生影响,未来可以研究不同学习率下参数Cr的取值影响以及参考GA等传统算法中对突变概率参数的相关理论研究。算法的近邻场局部搜索机制使算法保持了较好的种群多样性,在此基础上如何提升算法的全局搜索性能,以及探讨不同寻优机制对算法的影响仍然具有研究意义。此外,可以借鉴其他局部搜索算法如爬山法、模拟退火、禁忌搜索以及变邻域搜索等对NFO的近邻场寻优机制作进一步探索和研究,并分析算法的鲁棒性、复杂度以及收敛性等特性以及其中的影响因素,为算法未来的发展提供更坚实的理论基础。
(2)NFO算法改进研究。就目前来看,NFO算法现有的改进内容以及改进方式都较少,仍然存在进一步研究和探索的空间。近邻场搜索机制作为一种局部搜索,如何提升算法的全局搜索能力是目前算法改进的重点,现有改进策略如NFO-n、DNFO 以及NFO-DE 算法通过改进近邻场机制的搜索范围提升全局搜索性能,ABNFO算法引入了精英个体扩大搜索范围。算法学习率a控制个体的搜索范围,但目前相关的改进研究较少,因此未来也可以针对算法参数改进来提高算法搜索步长,除此以外,可以引入交流算子,在定位操作中增加随机搜索机制等方式提高搜索能力。初代种群结构和质量对近邻场算法性能也有一定影响,就目前来看,现有的相关改进研究较少,未来可以考虑引入混沌映射、反向学习以及莱维飞行等思想缩小初始解的随机性和不确定性,或者采用对初始种群分组优化以及多种群协同优化等方法。此外,在混合算法方面,可以考虑融合一些其他经典智能优化算法如狼群算法、模拟退火算法[44-45]等来平衡算法局部搜索和全局搜索能力,或者借鉴繁殖、克隆以及多邻域等机制来增强算法各方面性能。在个体迭代中可以考虑加入随机游走策略以及变异扰动策略等减少寻优误差。在参数控制方面可以考虑增强参数的自适应性从而增强算法的稳定性。目前算法的改进研究主要为单目标NFO 算法的相关改进研究,未来对于多目标NFO算法的改进研究也值得探索。
(3)NFO 算法应用研究。文中可以看到NFO 算法及其改进算法已经应用在多种领域中解决相关优化问题,但实际上其中较多都为参数优化问题或仅是对一些基准函数的测试问题。并且算法较多的应用场景集中在单目标优化问题,对一些实际复杂的多目标、离散或动态不确定问题的应用较少。此外,算法的应用领域也并不广阔,应用研究主要集中在能源效率或者建筑节能改造优化领域等相关领域,此外如调度问题、路径规划、图像信号处理以及神经网络等其他领域的应用研究,在未来的研究中是值得尝试的。
