Q690D和Q460D钢板对接焊缝的疲劳寿命计算

黄益洲, 王万祯*, 李草原

Q690D和Q460D钢板对接焊缝的疲劳寿命计算

黄益洲1, 王万祯1*, 李草原2

（1.宁波大学 土木与环境工程学院, 浙江 宁波 315211; 2.宁波大学 海运学院, 浙江 宁波 315832）

采用新近提出的统一计及疲劳裂纹形成寿命和稳定扩展寿命的结构钢疲劳寿命计算模型, 对Q690D和Q460D钢板对接焊缝疲劳试验进行疲劳寿命计算. 假设高强钢板对接焊缝的疲劳裂纹起裂于对接焊缝边缘, 沿板宽扩展且穿透板厚, 可将高强钢板对接焊缝疲劳断裂面积分为疲劳裂纹稳定扩展面积f和失稳扩展面积n(即名义最大应力作用下的净截面强度拉断面积). 以结构钢的椭球面断裂模型为判据, 由高强钢板对接焊缝疲劳裂纹的裂尖真实应力场解得高强钢板对接焊缝疲劳裂纹的失稳扩展面积n、稳定扩展面积f和稳定扩展长度f. 计算结果表明: 不同屈服强度下的高强钢板对接焊缝的疲劳寿命相差较大, 应采用各自量化的疲劳寿命计算式; 本文量化的结构钢疲劳寿命计算式对Q690D和Q460D钢板对接焊缝疲劳试验寿命的计算误差为-63.9%～-0.2%, 而现行规范建议的疲劳寿命计算式的计算误差为-70.7%～68.0%; 本文量化的结构钢疲劳寿命计算式的计算精度高于规范建议的疲劳寿命计算式, 前者计算结果对所有试件均偏于安全, 后者计算结果对部分试件偏于不安全, 且部分试件过于保守.

高强钢板; 对接焊缝; 疲劳寿命计算模型; 疲劳裂纹; 稳定扩展

随着钢材生产工艺的提高, 高强钢在建筑结构中得到应用, 我国《钢结构设计标准》规范新增了Q460高强钢[1]. 高强钢已成为钢结构领域的研究热点, 但对高强钢焊缝疲劳性能的研究非常有限[2-5]. 仇立宁等[6]分析了高碳钢滚动接触疲劳失效机理, 朱春莉等[7]研究了GCr15钢接触表面塑性形变强化与裂纹萌生机制, 郑荣跃[8]提出了疲劳裂纹扩展曲线的微分方程拟合法, 但以上研究均未涉及高强钢焊缝疲劳寿命计算.

由于对结构钢及焊缝疲劳裂纹形成、扩展至断裂全过程的极限状态及有关影响因素的研究还不足, 我国现行《钢结构设计标准》[1]采用式(1)建议的应力幅准则和允许应力法计算结构钢及焊缝的疲劳寿命, 而以前的《钢结构设计规范》[9]则采用最大应力准则来验算结构钢及焊缝的疲劳破坏.

结构钢及焊缝的疲劳破坏虽然积累了丰富的试验资料, 也能通过计算预估疲劳寿命, 但仍较多地依赖经验, 理论上并未真正解决[10].

结构钢疲劳破坏一般可分为疲劳裂纹形成、稳定扩展和失稳扩展三个阶段. 但结构钢焊缝不存在裂纹形成阶段[10-11], 因为焊缝在施焊时不可避免地存在气孔、夹渣、欠焊等缺陷, 这些缺陷即为初始裂纹(起裂源). 考虑到疲劳裂纹失稳扩展是瞬间断裂, 因此结构钢的疲劳寿命一般按疲劳裂纹形成寿命和扩展寿命之和计算, 前者如基于局部应力-应变法的Neuber模型[12], 后者如基于名义应力幅的Paris-Erdogan模型[13], 疲劳裂纹形成和扩展阶段分界线取裂纹长度0.02～0.05mm. 但应看到结构钢疲劳裂纹的形成和扩展是一个连续、渐变、完整、统一的自然演化(失效)过程, 有采用统一的疲劳寿命计算模型描述其总疲劳寿命的可能. 另外, 取疲劳裂纹长度0.02～0.05mm作为疲劳裂纹形成和扩展阶段的分界线, 很大程度上取决于裂纹观测仪器的灵敏度, 如采用更灵敏的裂纹观测仪器(如0.005、0.01mm), 应能观测到更小裂纹尺寸的疲劳裂纹形成和扩展阶段分界线.

众所周知, 疲劳裂纹随循环加载次数增加而加速扩展, 即同样的疲劳裂纹扩展长度在循环加载早期和后期, 或人为划分的疲劳裂纹形成和扩展阶段, 所需的循环加载次数会相差较大. 若疲劳裂纹形成和扩展阶段分界线裂纹长度取值不同, 如0.02、0.05mm等, 则因疲劳裂纹形成和扩展阶段采用不同的疲劳寿命计算模型, 也势必导致计算的总疲劳寿命相差较大.

基于上述考虑, 本文采用文献[14]提出的统一计及疲劳裂纹形成寿命和稳定扩展寿命的结构钢疲劳寿命计算模型对Q690D和Q460D钢板对接焊缝疲劳试验进行疲劳寿命计算, 验证其计算精度和普适性.

1 高强钢板对接焊缝的疲劳寿命计算模型

1.1 高强钢板对接焊缝的疲劳寿命计算式

疲劳裂纹扩展速率是决定高强钢板对接焊缝疲劳寿命的关键因素, 受到了广泛关注[4-5,12-13,15-23].

文献[14]基于结构钢疲劳裂纹随加载次数加速扩展的试验事实, 以结构钢疲劳裂纹的稳定扩展速率(一次循环加载下疲劳裂纹扩展长度)为循环加载次数的单调递增幂函数为假定, 即双对数坐标系下高强钢疲劳裂纹的稳定扩展速率是循环加载次数的单调递增线性函数, 积分导出统一计及疲劳裂纹形成寿命和稳定扩展寿命的结构钢疲劳寿命计算模型:

式(2)建议的结构钢疲劳寿命计算模型克服了《钢结构设计标准》[1]建议的疲劳寿命计算式, 即式(1)等式两端量纲不同的缺陷.

参数、取决于钢种、试件几何形状(应力集中程度)、载荷参数等, 由疲劳试验数据拟合标定.

1.2 高强钢板对接焊缝的疲劳裂纹稳定扩展长度

图1和图2是文献[3]进行的Q460D钢板对接焊缝疲劳的试验照片. 由图可见, 疲劳断裂面分为贝纹状的疲劳裂纹稳定扩展区和粗糙的疲劳裂纹失稳扩展区; 疲劳裂纹萌生于焊接热影响粗粒区或熔合区, 呈放射状向板侧边扩展且穿透板厚. 图2的对接焊缝疲劳断口电镜扫描照片显示, 疲劳断口分为疲劳裂纹源、疲劳裂纹稳定扩展和瞬断区, 疲劳裂纹稳定扩展区断面光滑, 有向外放射状疲劳条带, 撕裂棱将不同晶粒间的疲劳条带相连; 瞬断区有明显的韧窝和解理台阶.

图1 Q460D钢板对接焊缝的疲劳试验破坏照片

图2 对接焊缝疲劳断口电镜扫描照片

基于图1与图2所示的Q460D钢板对接焊缝的疲劳试验结果[3], 假设高强钢板对接焊缝的疲劳裂纹起源于对接焊缝一侧边的焊接熔合区, 向对接焊缝另一侧边扩展, 且穿透焊缝厚度. 则高强钢板对接焊缝的疲劳裂纹稳定扩展长度(f)为:

式中:为对接焊缝厚度;0为初始缺陷尺寸;f为疲劳裂纹稳定扩展面积.

1.3 高强钢板对接焊缝的疲劳裂纹稳定扩展面积

按前所述, 高强钢板对接焊缝的疲劳断裂面分为贝纹状的疲劳裂纹稳定扩展区和粗糙的疲劳裂纹失稳扩展区, 则包含初始裂纹或缺陷尺寸0效应的疲劳裂纹稳定扩展面积为(f):

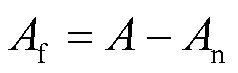
式中:为对接焊缝全截面断裂面积;n为疲劳裂纹失稳扩展面积.

1.4 高强钢板对接焊缝的疲劳裂纹失稳扩展面积

为计算高强钢板对接焊缝的疲劳裂纹失稳扩展面积n, 需求解高强钢板对接焊缝疲劳裂纹的裂尖真实应力场, 并选用能描述高强钢板对接焊缝疲劳裂纹裂尖在复杂应力状态下的断裂判据.

文献[24]以结构钢在三向等拉伸应力状态下断裂和屈服近似重合为保守假设, 提出的结构钢椭球面断裂模型及耦联的椭球面屈服模型分别为:

y、u、f和分别为疲劳裂纹裂尖的Mises等效应力、平均应力、对接焊缝的剪切屈服强度、剪切断裂强度、单向拉伸屈服强度、单向拉伸极限强度、单向拉伸断裂强度和泊松比.

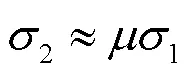
则高强钢板对接焊缝疲劳裂纹裂尖应力场为:

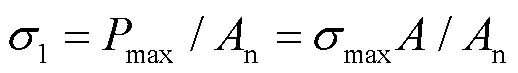
将式(7)计算的高强钢板对接焊缝疲劳裂纹裂尖应力场代入式(5)建议的结构钢椭球面断裂模型, 解得高强钢板对接焊缝的疲劳裂纹失稳扩展面积:

2 高强钢板对接焊缝的疲劳寿命计算

文献[2-3]对图3所示的厚度为8mm的Q690D和Q460D轧制钢板“V”形坡口全焊透对接焊缝进行了疲劳试验, Q690D和Q460D钢板采用的焊条分别为CHE857Cr和CHE557RH, 均采用手工电弧焊焊接, 焊后保留焊缝余高, 焊缝质量等级为一级. 疲劳试验前经查, 各试件对接焊缝无微裂纹等明显缺陷.

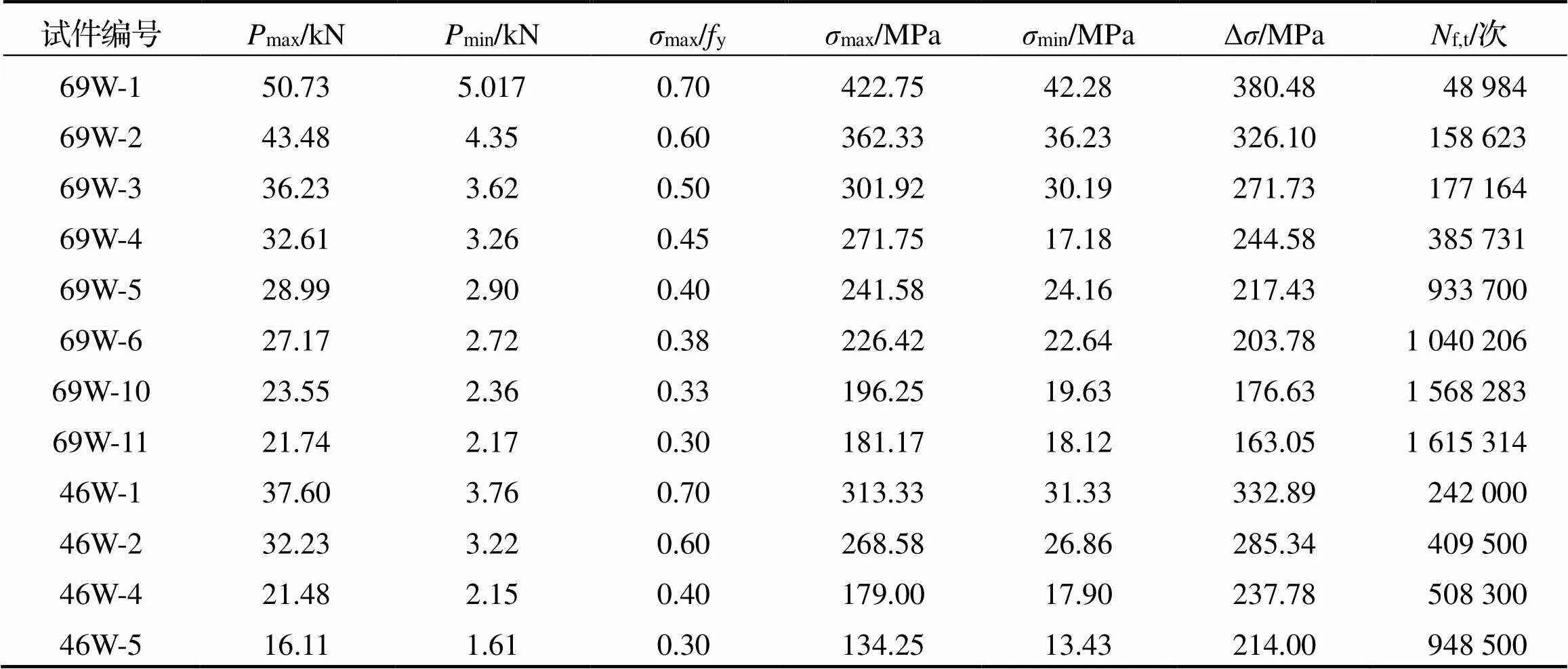
表1 Q690D和Q460D钢板对接焊缝疲劳试验加载参数和试验结果

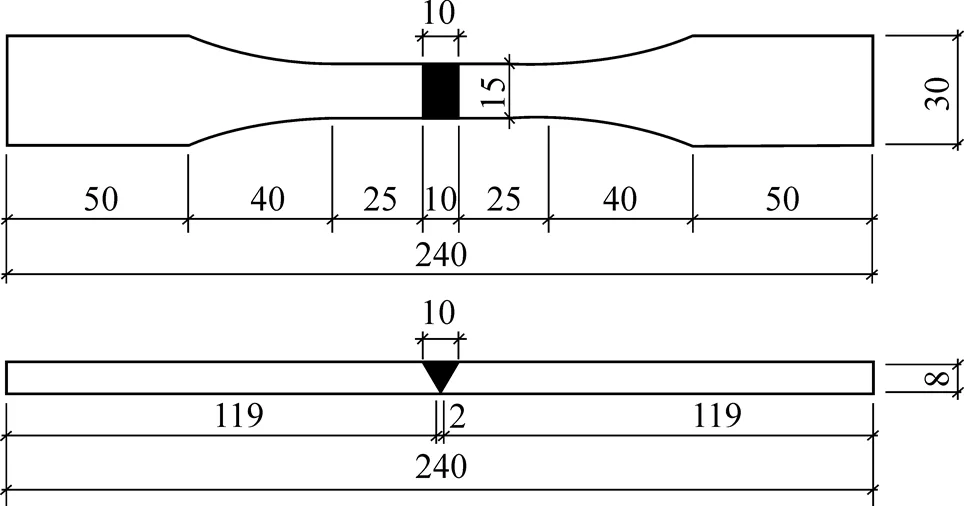
图3 Q690D和Q460D钢板对接接头试件尺寸(mm)

疲劳试验结果显示, Q690D和Q460D钢板对接焊缝的疲劳寿命具有较大离散型, 但仍表现出明显规律, 即疲劳寿命随应力幅的增加而降低.

筛选出符合疲劳寿命随应力幅的增加而降低规律的Q690D和Q460D钢板对接焊缝疲劳试验试件, 其试验结果列于表1, 其中,f,t为疲劳寿命试验值. 需要说明的是, 为区分Q690D和Q460D试件并尽量保持文献[2-3]中对接焊缝试件的原始编号, 表1对Q690D和Q460D试件进行重新编号, 如试件69W-1对应文献[2]中的Q690D钢板对接焊缝试件B-1, 其余相同.

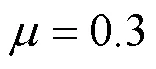
表2 Q690D和Q460D钢板对接焊缝材性数据

椭球面断裂模型参数.

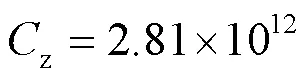
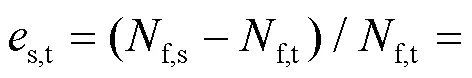
将式(2)建议的高强钢板对接焊缝的疲劳寿命计算模型改写为双对数坐标:

按式(9)对表3中各试件疲劳寿命试验值f,t和疲劳裂纹稳定扩展长度f进行拟合, 结果如图4所示, 并且Q690D和Q460D钢板对接焊缝的疲劳寿命计算模型参数、的标定结果列于表3. 由表可见, 参数、随对接焊缝强度变化较大, 不同屈服强度的高强钢板对接焊缝应采用不同的疲劳寿命计算模型参数.

图4 钢板对接焊缝af和Nf的拟合函数

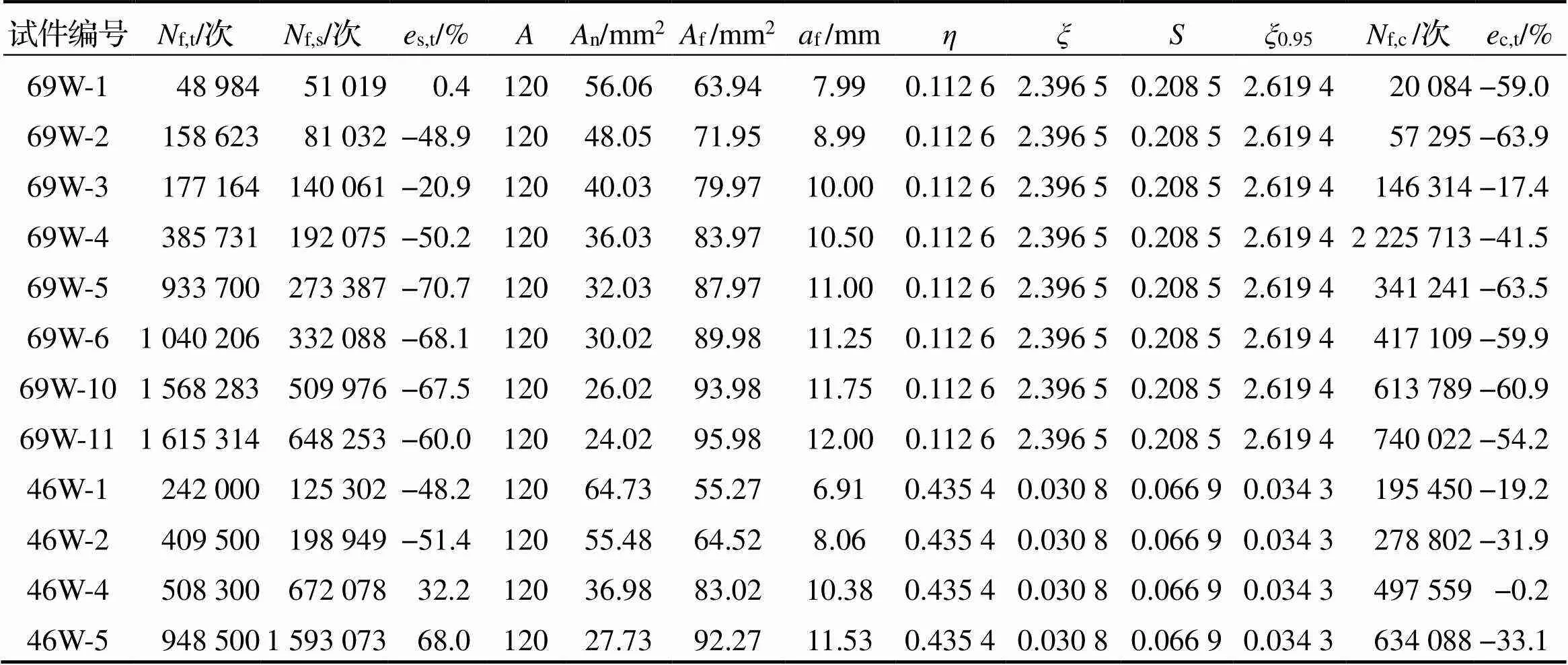
表3 Q690D和Q460D高强钢开孔板的疲劳寿命计算模型参数标定

在式(9)中引入各试件疲劳寿命计算值的1.645倍标准差,得式(10). 对表3中各试件的疲劳寿命试验值f, t和疲劳裂纹稳定扩展长度f按式(10)重新拟合(图5), 得95%保证率的高强钢板对接焊缝的疲劳寿命计算模型参数0.95(表3).

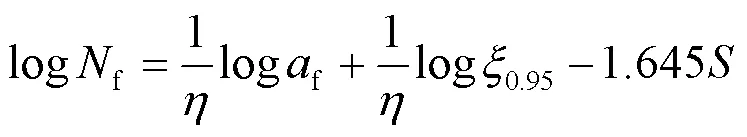
再按式(10)计算各试件疲劳寿命f,c及与试验值的相对误差c,t, 由表3可见, 式(10)建议的高强钢板对接焊缝的疲劳寿命算式对Q690D和Q460D钢板对接焊缝的疲劳寿命计算偏于安全, 与试验值的相对误差为-63.9%～-0.2%, 计算精度高于《钢结构设计标准》[1]的计算结果.

3 结论

采用统一计及疲劳裂纹形成寿命和稳定扩展寿命的结构钢疲劳寿命计算模型对Q690D和Q460D钢板对接焊缝进行疲劳寿命计算, 得到以下结论: (1)量化的高强钢板对接焊缝疲劳寿命算式对Q690D和Q460D钢板的计算误差为-63.9%～ -0.2%; (2)现行设计规范建议的疲劳寿命计算式对Q690D和Q460D钢板的计算误差为-70.7%～68.0%. (3)量化的结构钢疲劳寿命算式对Q690D和Q460D钢板的计算精度高于规范建议的疲劳寿命计算式, 前者计算结果对所有试件均偏于安全, 后者计算结果对部分试件偏于不安全, 部分试件过于保守.

[1] GB50017-2017. 钢结构设计标准[S].

[2] 郭宏超, 万金怀, 刘云贺, 等. Q690D高强钢焊缝连接疲劳性能试验研究[J]. 土木工程学报, 2018, 51(9):1-9.

[3] 郭宏超, 郝李鹏, 李炎隆, 等. Q460D高强钢及其焊缝连接疲劳性能试验研究[J]. 建筑结构学报, 2018, 39(8): 157-164.

[4] 宗亮, 施刚, 王元清, 等. WNQ570桥梁钢及其对接焊缝疲劳裂纹扩展性能试验研究[J]. 工程力学, 2016, 33 (8):45-51.

[5] 施刚, 张建兴. 高强度钢材Q460C及其焊缝的疲劳性能试验研究[J]. 建筑结构, 2014, 44(17):1-6.

[6] 仇立宁, 李淑欣, 蒋港辉, 等. 无碳化物贝氏体高碳钢滚动接触疲劳失效分析[J]. 宁波大学学报(理工版), 2021, 34(2):55-60.

[7] 朱春莉, 赵凤平, 苏云帅. GCr15钢接触表面塑性形变强化与裂纹萌生机制[J]. 宁波大学学报(理工版), 2019, 32(6):61-66.

[8] 郑荣跃. 疲劳裂纹扩展曲线的微分方程拟合法[J]. 宁波大学学报(理工版), 2004, 17(3):264-267.

[9] TJ17-74. 钢结构设计规范[S].

[10] 沈祖炎, 陈扬骥, 陈以一. 钢结构基本原理[M]. 2版. 北京: 中国建筑工业出版社, 2005:66-77.

[11] 陈绍蕃, 顾强. 钢结构(上册)—–钢结构基础[M]. 北京: 中国建筑工业出版社, 2003:301-315.

[12] Neuber H. Theory of stress concentration for shear- strained prismatical bodies with arbitrary nonlinear stress- strain law[J]. Journal of Applied Mechanics, 1961, 28(4): 544-550.

[13] Paris P C, Erdogan F. A critical analysis of crack growth laws[J]. Journal of Basic Engineering, 1963, 85:528-534.

[14] 王万祯. Q345圆钢杆的疲劳破坏模型[J]. 哈尔滨工业大学学报, 2019, 51(12):121-127.

[15] Foeman R G, Kearney V E, Eegle R M. Numerical analysis of crack propagation in cyclic-loaded structure [J]. Journal of Basic Engineering, 1967, 89(3):459-464.

[16] Elber W. The significance of fatigue crack closure[C]. Damage tolerate in aircraft structures, ASTM STP 46, Philadelphia: American Society for Testing and Material, 1971:230-242.

[17] 王春生, 段兰, 郑丽, 等. 桥梁高性能钢HPS 485W疲劳裂纹扩展速率试验研究[J]. 工程力学, 2013, 30(6): 212-216.

[18] 杨冰, 赵永翔, 梁红琴, 等. 基于Elber型方程的随机疲劳长裂纹扩展概率模型[J]. 工程力学, 2005, 22(5): 99-104; 125.

[19] 赵永翔, 杨冰, 张卫华. 一种疲劳长裂纹扩展率新模型[J]. 机械工程学报, 2006, 42(11):120-124.

[20] 关鹏涛, 闾川阳, 唐夏焘, 等. Q345R钢多个过载作用下疲劳裂纹扩展行为研究[J]. 工程力学, 2017, 34(7): 224-231; 240.

[21] 赵兴华, 蔡力勋, 包陈. CRO试样的疲劳裂纹扩展行为试验方法研究[J]. 工程力学, 2016, 33(11):20-28.

[22] 黄学伟, 蔡力勋, 包陈, 等. 基于低周疲劳损伤的裂纹扩展行为数值模拟新方法[J]. 工程力学, 2011, 28(10): 202-208.

[23] 刘艳萍, 陈传尧, 李建兵, 等. 14MnNbq焊接桥梁钢的疲劳裂纹扩展行为研究[J]. 工程力学, 2008, 25(4):209- 213.

[24] 王万祯. 结构钢开裂准则及断裂试验分析[J]. 工程力学, 2008, 25(5):27-31.

[25] 施刚, 林错错, 周文静, 等. 460MPa高强钢箱形截面轴压柱局部稳定有限元分析和设计方法研究[J]. 工程力学, 2014, 31(5):128-136.

Fatigue life calculation of butt weld of Q690D and Q460D steel plates

HUANG Yizhou1, WANG Wanzhen1*, LI Caoyuan2

( 1.School of Civil and Environmental Engineering, Ningbo University, Ningbo 315211, China; 2.Faculty of Maritime and Transportation, Ningbo University, Ningbo 315832, China )

The test fatigue life of butt weld of Q690D and Q460D steel plates was calculated by using a newly proposed fatigue life calculation model of structural steel, which takes into account the fatigue crack forming life and stable growth life. It is assumed that the fatigue crack of butt weld of high strength steel plates starts from the edge of butt weld and propagates along the width of plate and penetrates the thickness of plate. The fatigue fracture areaof butt weld of high strength steel plates was divided into two parts: the stable propagation areafof fatigue crack and the unstable propagation areanof fatigue crack (i.e. the tensile fracture area under the nominal maximum stress). The instability propagation arean, stable propagation areafand stable propagation lengthfof fatigue crack of butt weld of high strength steel plates were calculated according to the true stress field of fatigue crack tip by using an elliptical fracture model of constructional steel as fracture criterion. The calculation results show that the fatigue life of butt weld of high strength steel plates with different yield strength is quite different, and should be calculated by their own quantitative fatigue-life formula. The calculation error of the quantitative fatigue life calculation formula in this paper is -63.9% – -0.2% for the fatigue life of butt weld of Q690D and Q460D steel plates, while the calculation error of fatigue life formula recommended by current code is -70.7% – 68.0%. The calculation accuracy of the quantitative fatigue life calculation formula in this paper is higher than that recommended by current code. The former is safe for all specimens, while the latter is unsafe for some specimens and too conservative for others.

high strength steel plate; butt weld; fatigue life calculation model; fatigue crack; stable propagation

通信作者:王万祯（1974－）, 男, 河南周口人, 博士/教授, 主要研究方向: 钢结构断裂与疲劳. E-mail: wangwanzhen1975@sina.com

TU391

A

1001-5132（2022）03-0032-06

2021−03−04.

浙江省基础公益技术研究计划（LGF18E080007）.

黄益洲（1997－）, 男, 浙江台州人, 在读硕士研究生, 主要研究方向: 钢结构. E-mail: 936961204@qq.com

宁波大学学报（理工版）网址: http://journallg.nbu.edu.cn/

（责任编辑 章践立）