水位流量关系曲线延长方法的性能对比——以梅江水口(二)站为例

林博安

(广东省水利电力勘测设计研究院有限公司，广州 510635)

1 研究背景

水位流量关系作为水文资料整编的关键、河道水面线计算重要复核依据，其合理与否直接影响了水文资料整编的可靠性[1]。20世纪以来，受大规模人类活动及上游来水来沙条件改变的影响，梅江干流沿程河道断面变化剧烈[2-4]，以往水位流量关系曲线已不适用于现今河道断面，且近些年梅江流量较小，无法根据实测资料确定水位流量关系曲线，需进行断面水位流量关系的延长。

对断面水位流量关系曲线的延长，国内外研究者已经开展了大量工作，目前采用的方法大致可划分为依靠河道水力学规律的公式法，不考虑河道水力学规律仅依靠水位流量关系曲线数学模型的方法，两种方法应用均较为广泛。以往多数学者通过研究河道水力学规律，运用水力学公式推算水位流量关系曲线，较为常用的是通过曼宁公式法与斯蒂文斯法[5-7]定线推流；门玉丽等[8]采用运动波方程及扩散波方程来求解水位流量关系曲线，推出了水位流量关系双向转换的公式；袁帅等[9]为了解决欠缺实测水文控制断面资料而无法进行水位流量关系曲线经验拟合的问题，提出了一种以圣维南方程为理论基础的推导方法。

随着数学的发展，越来越多优化算法，使得水位流量关系曲线数学模型的参数优化求解变得可能，越来越多学者通过水位流量关系曲线数学模型法直接拟合水位流量关系。康玲等[10]使用小波分析、舒栋才等[11]使用免疫进化算法、李中志等[12]使用改进BP神经网络算法拟合水位流量关系，均得到了良好拟合效果。

目前以上两种方法均可应用于河道断面水位流量关系的拟合，但较少学者将两种方法进行性能比较。基于此，本文选取梅江流域水口(二)站进行分析，为其他水文站水位流量关系曲线延长时方法选取提供参考。

2 方法介绍

2.1 水力学公式法

水力学公式法可以减少水位流量关系曲线的高水延长中水位、流速顺势延长的人为任意因素，本质上是通过计算得出的流速值来辅助曲线延长。

2.1.1曼宁公式法(Manning Formula，MF)

1889年美国水利学者曼宁提出曼宁公式，曼宁公式一般表达式为：

(1)

式中：

v——河道流速；

n——河道糙率；

R——水力半径；

S——水面比降。

在对水位流量关系延长时，通过实测资料计算得到流速，进行水位面积关系曲线的延长，从而实现水位流量关系的延长。

因水力半径R可通过断面资料求得，故计算断面流速关键在于确定河道水面比降和糙率。如水面比降S与糙率n均无法确定时，将n-1S1/2看成一个未知数，依据实测资料通过下式计算出n-1S1/2，点绘Z～n-1S1/2曲线，因高水部分n-1S1/2近似于一个常数，故可沿平行于纵轴方向延长。

(2)

2.1.2斯蒂文斯法(Stevens，STE)

斯蒂文斯法利用谢才公式：

(3)

式中：

C——谢才系数(C=n-1R1/6)；

A——河道断面过水面积；其余符号同曼宁公式。

2.2 水位流量数学模型法

天然河道里稳定的水位流量关系可以抽象为一种非线性关系，概化后的数学模型形式可表示:

Q=a(H+b)c

(4)

式中:

Q——河道流量;

H——断面水位;

a、b、c——待拟定的模型参数。

为了正确得到待拟定的模型参数，避免目标函数陷入局部最优解问题，本文引入模拟退火算法、遗传算法及粒子群算法，综合计算待拟定的模型参数，各算法简介如下。

2.2.1模拟退火算法(Simulated Annealing，SA)

模拟退火算法是由N.Metropolis等人于1953年提出，基于固体物质的退火过程与一般组合优化问题之间的相似性[13]。主要原理主要是通过高温固体温度的不断下降，结合概率的突然跳跃特性，最终跳出问题的局部最优解，求得全局最优解。

2.2.2遗传算法(Genetic Algorithm，GA)

遗传算法是由Holland教授于1975年提出，起源于达尔文生物进化论的自然选择和遗传学机理的生物进化过程[14]。主要原理是通过解集的种群出发，不断进化，通过适者生存法则不断产生出更优解，每一代种群之间进行组合交叉与变异，逐步适应环境，进而得到问题的最优解。

2.2.3粒子群算法(Particle Swarm Optimization，PSO)

粒子群算法是在1995年由Eberhart和Kennedy博士提出，源于对鸟群捕食行为的研究[15]。主要原理是利用群体中的个体对信息的共享，使整个群体的运动在问题求解空间中产生从无序到有序的演化过程，从而获得问题的最优解。

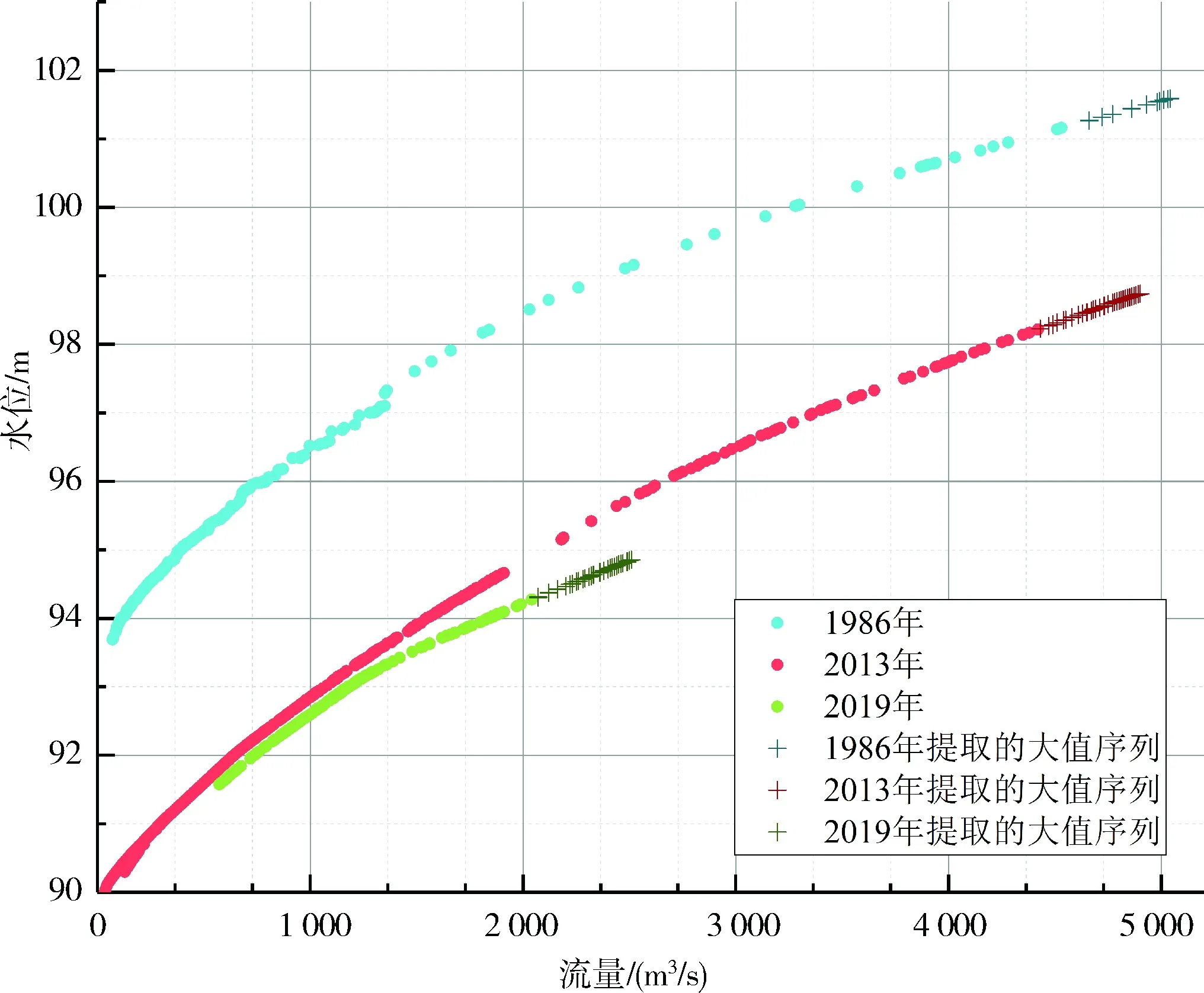
a 水口(二)水位流量关系散点

3 案例分析

3.1 研究区概况

梅江是韩江的主干流，发源于广东省河源市紫金县七星岽，上游称琴江，至五华县水寨镇与五华河汇合后称梅江，至梅州市大埔县与汀江汇合后称韩江。梅江河长为307 km，流域集雨面积为13 929 km2，自上而下建有近江、合江、龙上、三龙、西阳、丙村、单竹窝、蓬辣滩等8座梯级电站，水口(二)水文站位于合江及龙上电站之间。研究区域及水口(二)站位置见图1。

图1 研究区域及水口(二)位置示意

3.2 数据描述

本研究收集了梅江流域水口(二)站多年的实测洪水水文要素资料，资料可靠性强；由于本文研究结果考虑了人类活动对水文要素的影响，因此，资料一致性可不用考虑；选取了水口(二)站多年资料，涵盖了测站实测最大流量及最新资料，代表性强。

本次研究依据洪峰大小、年代远近等因素，分别选取了水口(二)站1986年、2013年以及2019年的河道大断面及洪水要素数据(见表1)，根据《韩江流域规划》中水口(二)站设计流量成果(见表2)可知，1986年洪水约为30年一遇，2013年洪水接近30年一遇，2019年洪水不到5年一遇。为了能够对延长的水位流量关系曲线进行验证，因此，本次研究将各个年份流量较大值的序列进行提取，作为未知数，对延长的流量进行实测数据对比，分析水位流量曲线延长的效果，不同年份提取序列信息见表1，水口(二)站实测数据示意见图2。

表1 水口(二)站不同年份数据主要信息 m3/s，m

表2 水口(二)站设计洪峰流量 m3/s

3.3 水力学公式法

表3 水口(二)站水位流量序列水力学公式法延长结果

3.3.1曼宁公式法(Manning Formula，MF)

从计算的Z～n-1S1/2曲线(见图3a)可知，在低水时n-1S1/2呈现波动上升的趋势，在高水时数值趋向平稳。通过提取的高水序列与延长后的序列的线性回归统计参数可知，1986年、2013年模拟的高水序列与提取的高水序列基本一致，且呈现高水部分逐渐贴合的正常现象，因此，可以认为计算参数可用于水位流量关系曲线的延长；2019年模拟的高水序列与提取的高水序列决定系数小于0，说明模拟的高水序列与提取的高水序列有很大不同。

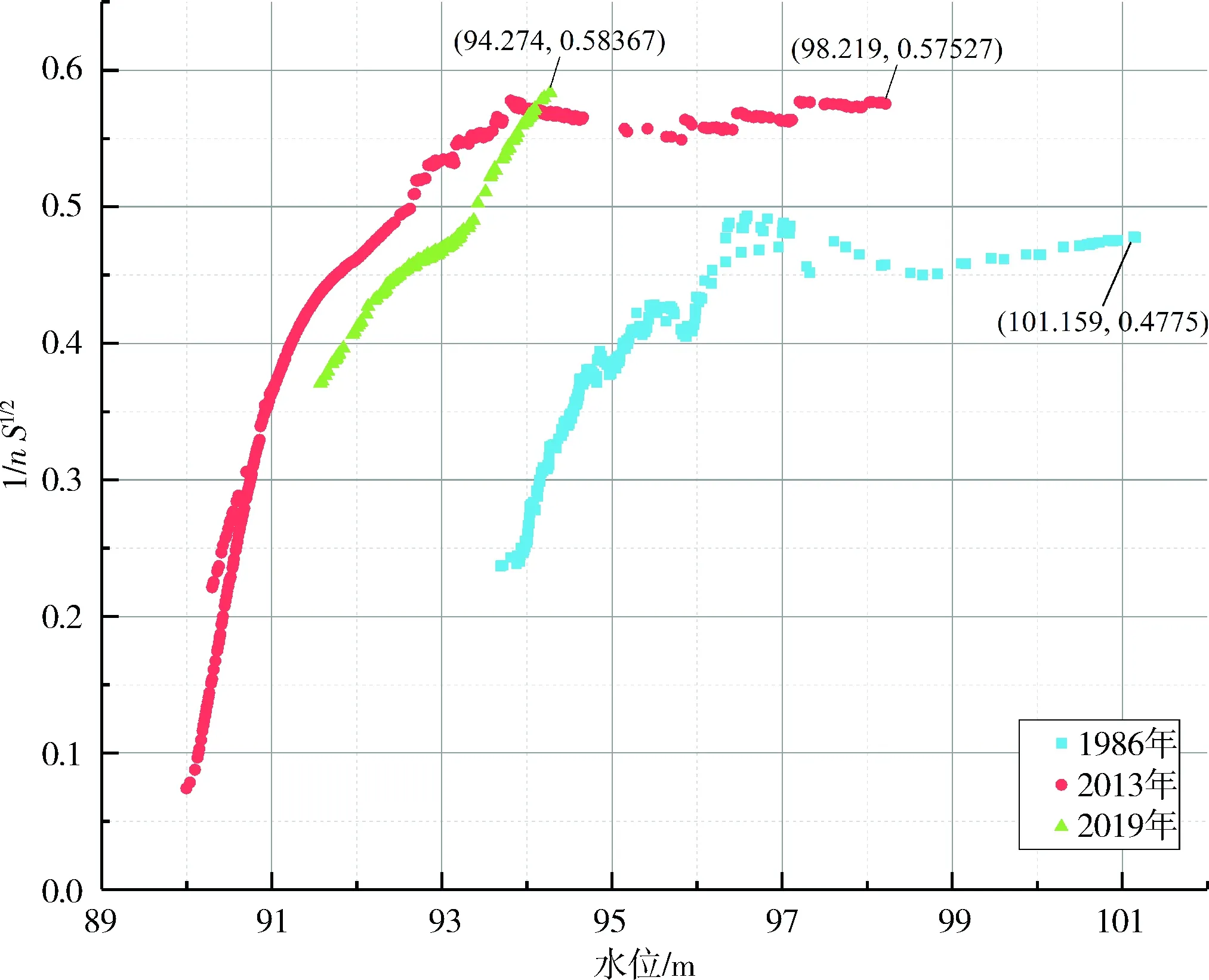
a Z～n-1S1/2曲线

以上说明，若年内观测流量足够大，使得计算得到的n-1S1/2位于平稳区间，其值作为高水延长的依据是可行的，并且能够较为有效的反映现实高水部分水位流量关系；而若年内观测流量小，计算得到的n-1S1/2依旧位于低水不稳定段，使用曼宁公式进行水位流量关系的延长，将会带来较大误差。

3.3.2斯蒂文斯法(Stevens，STE)

3.4 水位流量数学模型法

各方法拟合的水位流量关系曲线如图4所示，结果见表4所示。

表4 水口(二)站水位流量数学模型法结果

图4 水口(二)站水位流量数学模型法拟合效果示意

从模拟结果可知：

1)各方法拟合的数学公式结果说明，虽然各算法均能够跳出局部最优解去寻找全局最优解，但针对3参数的优化，每一个算法寻求的最优解均不相同，得到的目标函数值也均不同，而针对不同年份最优算法也不同，因此，在运用数学模型法进行水位流量关系延长时，需要综合不同的算法进行计算，定义合理的可能解取值域，对比分析最优算法及最优曲线。

2)1986年、2013年水位流量关系的延长结果表明，通过水位流量数学模型法可以较好的延长现有的水位流量关系，关联度、均方根误差及决定系数均表明模拟的高水序列与实测的高水序列基本一致，且相较于水力学公式，各年的最优算法的统计参数均较优，说明数学模型法在水位流量关系线性关系明显时，计算结果优于水力学公式法。

3)2019年结果表明，数学模型法用于拟合年内流量较小的水位流量关系时，类似于斯蒂文斯法，能够向上拟合一定区间内的水位流量关系，但延长较大的流量，就趋势而言，均会陷入错误的水位流量关系。

4)就模拟效果而言，不同的算法适用于不同年份的水位流量关系曲线，1986年最优算法是粒子群算法(PSO)，2013年最优算法是模拟退火算法(SA)，2019年最优算法是粒子群算法。换言之，各算法在不同年份均不可避免的陷入局部最优解的情况，以本文采用的计算代码及计算案例而言，最优算法应为粒子群算法，在1986年、2019年目标函数值最小，且虽然2013年目标函数值不是最小，但模拟的高水序列为最接近实测的高水序列。

残差绝对值和；Cov是数据关联度；RMSE是均方根误差；R2是决定系数。

3.5 综合分析

通过拟合的水位流量关系曲线，求对应设计频率流量下的测站水位(见表5所示)可知：有实测高流量年份(1986年、2013年)的各方法求解的结果差别不大，100年一遇情况下，各方法求解结果最大差值仅为0.27 m；缺失实测高流量年份的(2019年)，各方法求解结果差别较大，100年一遇情况下各方法求解结果最大差值为2.21 m。

表5 水口(二)站水位流量延长结果 m

将水力学公式法(曼宁公式法MF、斯蒂文斯法STE)拟合的曲线，水位流量数学模型法各优化算法中拟合最好的曲线进行比较(见图5)。结果可知，针对拥有高水流量的年份(1986年、2013年)水力学公式法、数学模型法拟合效果均较好，从对提取的实测高水流量拟合结果而言，数学模型法对高水延长效果更好；在水位流量关系曲线延长方面，水力学公式法计算得到的对应水位均高于数学模型法计算结果。当年内实测流量较小，如果仅通过小流量数据进行延长序列，将会陷入拟合较好但错误的曲线中，此时应通过曼宁公式法进行高水序列的延长，并结合往年水位流量曲线以及河道断面变化进行水位流量的矫正。

图5 水口(二)站水位流量拟合效果示意

水力学公式法中的斯蒂文斯法及数学模型法涉及目标函数的最值优化问题，其中斯蒂文斯法为单参数的函数优化求解，拟合过程较为简单；数学模型法涉及3参数的函数优化求解，为避免陷入局部最优解，可通过多种优化算法进行目标函数最值求解。而对于曲线方程而言，目标函数的确定则会很大程度的影响参数的优化求解，本文采用高水水位、流量与拟合结果的残差绝对值和最小作为目标函数，通过提取的高水资料对比模拟的高水资料结果证明该目标函数是可行的。但水位数学模型法涉及到的参数较多，虽然引入了优化算法极大的减小了函数陷入局部最优值的概率，但部分优化算法进行目标函数的优化求解时，依旧会陷入局部最优解无法跳出，应综合多种优化算法进行计算，并且结合测站多年的参数，规定合理的取值范围。

4 结语

本文选取了水力学公式法(曼宁公式法、斯蒂文斯法)及水位流量数学模型法，基于梅江水口(二)站3 a的实测水位流量数据，提取部分高水序列，对比分析了不同方法在测站水位流量关系曲线延长方面的性能差异，进一步探讨针对不同来水条件下各方法的适用性。实例分析结果表明：

1)针对有实测高流量年份(1986年、2013年)的水位流量关系延长，传统水力学公式及水位流量数学模型法拟合效果均较好。传统水力学公式方面，曼宁公式、斯蒂文斯法延长的流量与实测流量的R2均大于0.98，相较于曼宁公式，斯蒂文斯法结果更优；水位流量数学模型法方面，引入的SA、GA以及PSO优化算法均能够有效的优化求解目标函数，模拟的流量与实测流量R2最优算法均大于0.99，其中PSO算法表现更为优异。

2)针对有实测高流量年份的水位流量关系延长，水位流量数学模型法相较于传统水力学法而言，需要的数据量小且模拟效果更优，且由于优化算法的不断发展，能够较为有效的避免目标函数陷入局部最优值，针对3参数的目标函数优化求解变得容易，但研究结果证明：对3参数的优化求解，依然需要引入多个算法进行综合对比求解。

3)针对没有发生实测高流量年份的水位流量关系延长，通过传统水力学的斯蒂文斯法及水位流量数学模型法均容易陷入错误水位流量关系，为确保延长水位流量曲线，不出现明显因水库蓄水等人为因素影响低水水位流量关系而导致其余方法得到错误水位流量曲线，此时，可通过曼宁公式法进行水位流量曲线的延长。