基于爆破振速衰减规律的爆破振动控制技术

宋宏坤

(中铁十八局集团有限公司， 天津市 300222)

1 前言

爆破开挖技术在隧道掘进中广泛应用，其爆破作用效果对隧道掘进施工进度等起着至关重要的作用。但是爆破产生的振动效应会对周围环境以及建筑物构成危害。为了降低爆破振动造成的破坏和影响，需对爆破振动强度进行预测及控制。爆破振动质点峰值速度是描述爆破振动强度的代表性参数。因此，准确预测爆破引起的质点振动速度进而保证爆破工程安全顺利进行是控制爆破振动危害的主要方法[1-3]。

毕卫国等[4]提出解除萨氏公式的固定指数；梁书锋等[5]提出安全保证系数对于爆破振动衰减预测公式进行优化处理；万嗣鹏等[6-7]由量纲理论推导出考虑岩体抗拉强度的爆破振动速度衰减多元非线性数学模型以及基于准岩体强度推导爆破振动速度衰减改进公式；邵蔚等[8]考虑水深比的影响修正了传统的质点峰值振动速度公式，能够更好地反映水下爆破振动衰减规律；张勤彬等[9]建立了岩体累计损伤下爆破振动衰减规律的多元非线性数学模型；田乐等[10]结合实际工程案例，采用现场爆破试验与爆破振动测试相结合的方法，获得了层状岩体场地条件下爆破振动沿不同路径的传播与衰减特征；卢文波等[11]结合爆破振动频率衰减规律的量纲分析，推导出球形药包激发爆破振动主频的衰减公式；Marrara F, et al.[12]将高程差、地貌因素考虑在内，通过无量纲化处理，推导了改进的质点振动速度衰减公式；KAHRIMAN A[13]、AK H,et al.[14]、CHOI B H, et al.[15]、DEB D, et al.[16]通过爆破振动实测数据分析了边坡爆破振动速度衰减规律和高程放大效应等问题；孙鹏昌等[17]通过爆破振动实测数据分析和动力有限元数值模拟，分析了单薄山体岩质高边坡的爆破振动响应特征；王刚[18]提出了地下爆破振动作用下顺层陡高岩质边坡的动态时程稳定系数计算式，以评价隧道施工爆破振动对高边坡稳定性的影响；胡风明等[19]为防止爆破振动造成危岩带崩塌，提供了一种危岩带下锚碇基坑的施工技术方案，包括危岩处置和爆破方案设计，并对施工期爆破振动进行了监测。

上述研究从一些角度对爆破振速衰减公式进行了优化，建立了预测模型，取得了一定效果。但是关于自由面对爆破振动衰减的影响研究较少。而自由面的大小和数量影响着开挖爆破的效果，对于隧道爆破振速衰减有着重要影响。该文以萨道夫经验振速衰减公式为基础，将自由面面积参数引入到公式中，改进爆破峰值振动速度公式。以大前石岭隧道为例，进行现场爆破振速监测试验，验证爆破振速衰减规律，并提出爆破施工安全距离计算公式和相应爆破振动控制措施。

2 爆破振动速度衰减公式优化

2.1 爆破振动速度预测公式

通常以预测质点峰值振动速度控制爆破有害效应，但是预测精度问题始终困扰着爆破行业。国内外研究人员通过大量工程经验和研究，提出了不同的爆破振动速度经验公式。目前中国应用较为广泛的是苏联的萨道夫斯基所提出的爆破振动峰值振速经验公式：

(1)

式中：V为爆破峰值振速(cm/s)；Q为炸药量(kg)；R为爆源距(m)；K、q为场地系数。

2.2 自由面对爆破振动速度衰减的影响

被爆破的岩石与空气接触的表面称为自由面。自由面的面积越大，自由面数量越多，爆破效果越好。自由面是影响爆破效果的重要因素之一。为此，利用Ansys软件LS-DYNA模块仿真建模模拟隧道开挖面爆破过程，探讨自由面对爆破振速的影响，并依据影响规律将其引入预测公式中。

为研究自由面对爆破振动振速衰减的影响，通过Ansys/LS-DYNA建立隧道轮廓相同、截面积不同的3个模型进行对比试验，模拟隧道开挖至40 m处。模型共5个版块：围岩、初期支护、二次衬砌、空气和炸药。由于模型尺寸限制，为避免爆破振波因模型外边界反射影响，模型边界条件考虑为：除隧道内部表面为自由边界以外，其他边界设置为无反射边界。隧道模型图见图1。

图1 隧道模型

3个模型轮廓均为：长×宽×高=50 m×17 m×14 m。数值模型模拟隧道全断面爆破开挖，爆破自由面和隧道开挖截面可视为同一平面，取自由面面积等于隧道截面面积。模型Ⅰ、Ⅱ、Ⅲ截面面积分别为60.05、38.43、21.62 m2。3个隧道中轴线相同。模型网格尺寸为0.25 m×0.25 m，炸药置于隧道内中心位置，选用中心掏槽爆破荷载作为动力荷载，3次模拟炸药量保持一致。每个模型选取7个监测点，如图2所示，获得21组监测点数据。监测点位于隧道模型顶部围岩部分，3个模型除隧道截面面积不一致外其余参数保持一致，固定监测点与爆源点，保证3个模型爆源距相等，监测点设置呈一条直线，各点间隔距离为等差数列，公差为0.667 m，首项5 m。设定的围岩物理参数见表1，炸药设置参数见表2。

图2 监测点分布

表1 围岩物理参数

表2 炸药设置参数

LS-DYNA模块模拟高能炸药爆破压力-体积关系使用JWL状态方程。JWL状态方程如下：

(2)

式中:V为相对体积；E0为初始内能密度；参数ω、R1、R2、A、B为试验确定的常数。炸药相关参数取值见表3。

表3 JWL状态方程参数取值

分别运行3个数值模型，得到各监测点振动响应，提取峰值振速，汇总见表4。由模拟结果发现：随着监测点距离的不断增加，爆破振动峰值振速逐渐降低，符合爆破振速衰减规律；对比相同距离监测点的峰值振速发现，随着隧道截面面积减小，质点峰值振速逐渐增加。在隧道围岩参数相同和炸药量相同条件下，自由面面积越小则引起的质点峰值振速越强烈。因此，爆破过程中自由面面积对质点峰值振速的影响较大，且自由面面积与爆破引起的质点峰值振速呈负相关。

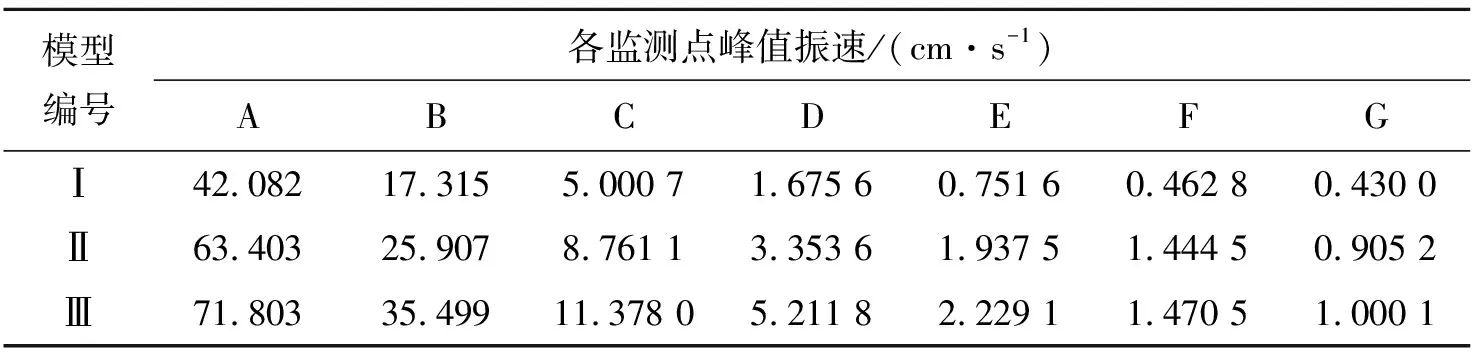
表4 模型监测点峰值振速

2.3 自由面面积参数引入

考虑将自由面面积因素引入到振动速度计算公式中，以萨道夫峰值振动衰减公式为依托，改进峰值振速公式。因为自由面面积越大引起周围爆破振动越小，因此添加自由面因子以及面积指数，且面积指数通常为负数。

在萨道夫公式(1)中添加自由面面积S及面积指数β，改进后得到式(3)：

(3)

3 隧道爆破振动现场监测

3.1 工程概况

大前石岭隧道位于辽宁省本溪市桓仁满族自治县境内，进口在八里甸子镇三道河村东南侧约900 m，出口在普乐堡镇姜家堡子村西侧约1.7 km，起讫里程为DK69+225 ～DK71+680，全长2 460 m。

隧道按新奥法原理组织施工，开挖采用光面爆破技术。炸药采用2号岩石乳化炸药，装药方式采用耦合装药，炸药钻孔直径40 mm，孔深3～4 m。炸药密度为1 200 kg/m3，炸药爆速为4 500 m/s，岩石压缩波传播速度为4 656.875 m/s，岩石密度为2 706 kg/m3。绝热指数取3。

3.2 隧道爆破振动监测

爆破振动监测选用由中国地震局地质研究所研发的新版数据采集系统，包括传感器、电缆、数据集线器、转换器、主机5部分。爆破试验信号采样频率为50 kHz。爆破振动监测设置6个监测点，共进行5次爆破试验，理论可获得30个爆破振动速度波形。爆破炸药量以及自由面面积有所变化。第3次爆破时增加爆破避车洞。5次爆破炸药用量及自由面面积见表5。监测点固定到隧道内部右侧。监测点的命名为两位数字，第一位数字代表爆破的序号，第二位数字代表监测点的位置。如3-2表示第3次爆破2号监测点。各监测点距爆破自由面距离以及统计5次爆破各监测点峰值振速见表5。

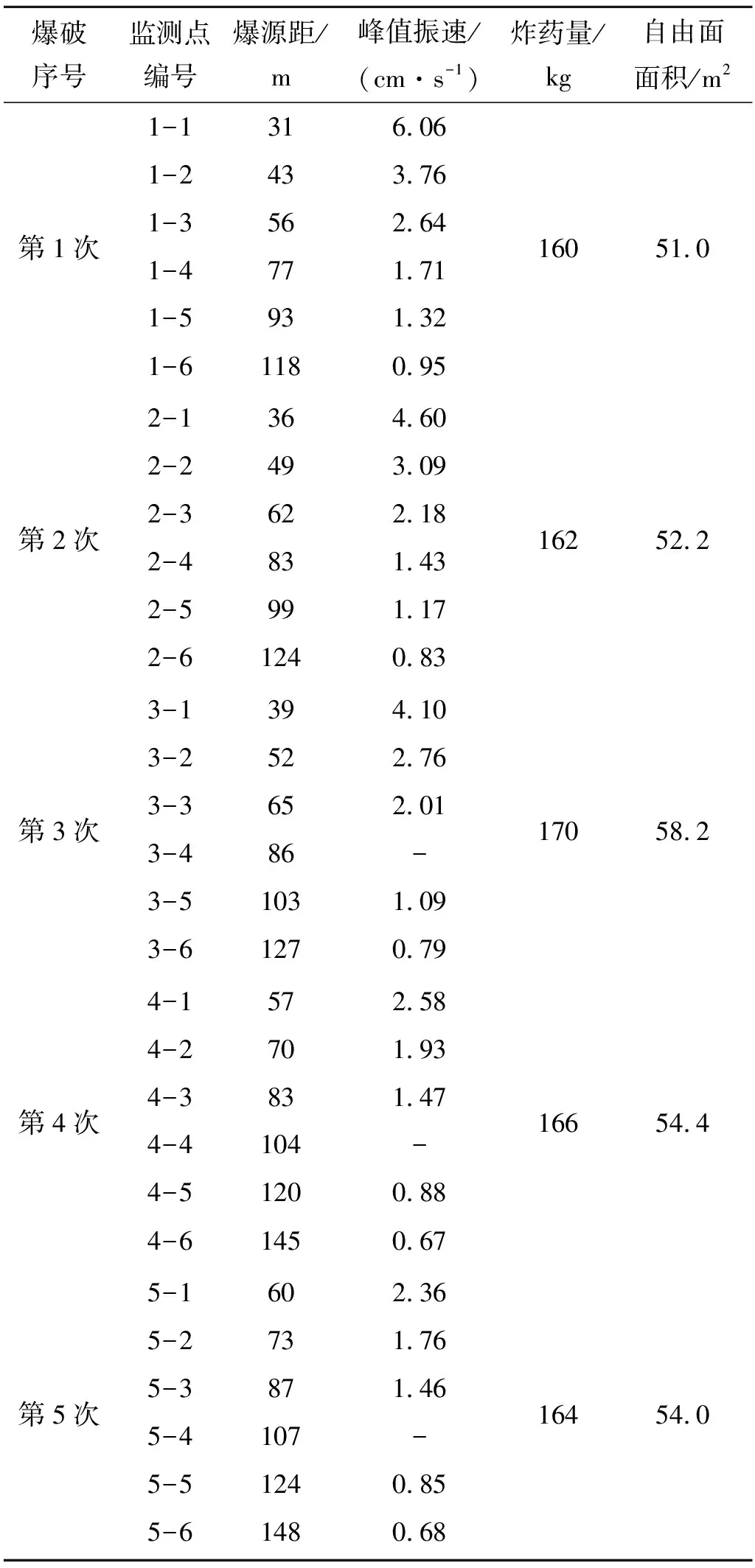
表5 监测点数据

3.3 爆破振动质点峰值速度预测分析

表4中的质点峰值振速数据按照萨道夫斯基公式(1)和改进公式(3)进行回归计算对公式进行拟合，寻求公式衰减系数，结果见表6。

表6 衰减公式系数计算

表6给出了表征拟合效果的4个拟合参数，分别是和方差(SSE)、标准差(RMSE)、确定系数(R2)和修正确定系数(AdjustedR2)，均由Matlab Curve Fitting Tool产生。其中SSE和RMSE越接近0，R2和AdjustedR2越接近1，表征拟合模型选择更优，数据预测更准确。由此可反映改进公式较原公式预测效果更佳。

为了避免计算样本和检验样本相同，故采用前4组试验数据为计算样本，第5组数据为检验样本。将参数分别代入各公式中，再预测第5次爆破质点峰值振速，将计算结果与第5次爆破振动监测数据相比较见表7。

表7 第5次爆破振速峰值及预测结果对比

由表7可知：预测结果与现场实际监测数据虽然有一定差异，但变化趋势相同。近距离监测点的预测结果偏小，远距离监测点的预测结果偏大。预测结果与监测结果接近。

表8为两个公式预测值与实际监测值的误差分析结果。预测结果的绝对误差均低于0.08 cm/s，相对误差不超过5%。对于严格预测隧道爆破质点峰值振速，质点峰值振速改进公式有一定的意义。

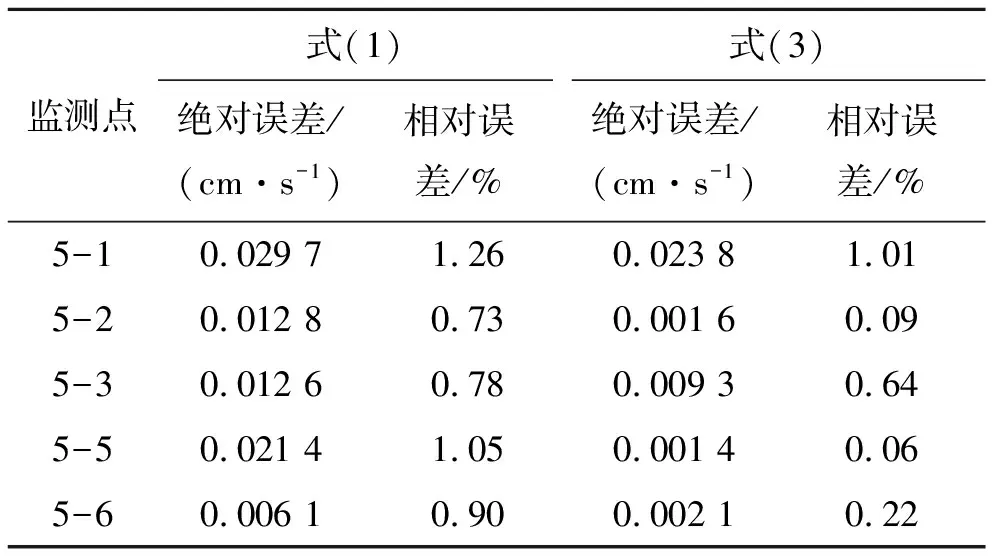
表8 预测值与实际监测值误差分析

4 爆破振动控制技术

4.1 爆破振动安全距离确定

爆破施工会对周围地段环境产生影响，因此，预先进行振动安全影响评估，既能保证自身的合法利益不受侵害，又能对周围环境起到保护作用。在爆破工程施工中，为确保保护对象的安全，需将爆破振动强度控制在一定临界值内。若强度超过此临界值，就可能引起保护对象的破坏。这个爆破振动强度的临界值称为爆破振动安全判据。

通过前文建立的改进爆破振速预测公式，推导安全距离计算公式见式(4)：

(4)

隧洞周边被保护建筑物多为砖混结构及部分土木结构，参照GB 6722—2014《爆破安全规程》中“土坯房”的爆破振动安全标准，且一般浅孔爆破振动频率为40～100 Hz，故选取爆破振动安全允许振速为0.7～1.5 cm/s[20]，考虑到民房的修建年限和修建质量，经科学分析，周边民房的爆破振动安全允许评估标准采取谨慎原则，降低一个等级，最终确定为0.5 cm/s。以安全允许振动速度0.5 cm/s为允许承受的振动强度指标，计算出不同条件下被保护地面建筑物不受爆破振动危害影响的安全距离临界值。

采用表2和第5次爆破参数按式(4)计算，爆破振动安全距离为191.76 m。

4.2 爆破振动控制措施

(1) 创造更多、更大的自由面

数值计算和大前石岭隧道现场爆破试验结果表明：自由面面积与振速呈负相关。自由面面积越大则引起周围的振动越小，靠近自由面的炮孔爆破产生的爆破振动具有良好的松动条件。施工中配合炮孔布置，选用小孔径炮孔爆破，在创建充足自由面和获得围岩最大松动的同时，充分降低爆破振动幅度。由于大前石岭隧道采用微差爆破的方式，应当先引爆中间炮孔，刷大自由面，从而减弱爆破振动。

(2) 控制自由面上一次爆破炸药量

由萨道夫斯基经验公式(1)可知：一次爆破炸药量越多则引起的爆破振动将会越强烈。施工过程中，应严格控制自由面炸药量，通过安全距离和安全允许振速等反算进行控制。若出现需要增加爆破强度的情况，应在满足施工要求的前提下，采用分段爆破进行，包括炮孔内间隔分段、炮孔间分段和排间分段，最终实现施工要求。

(3) 炸药类型的选择

参考卢文波等建立的反映炸药性质、炸药类型、装药方式、炮孔大小以及围岩参数等对爆破振速影响的质点爆破振动速度公式[21]，可知炸药爆轰速度越大则引起的爆破振动越强，爆炸威力小、爆速低的炸药类型引起的围岩爆破振动效应较小。因此，施工中在炸药的可选范围内，选用威力小、爆速低的炸药以控制爆破振动负面效应带来的危害。

(4) 设置合适的爆破自由面网孔参数

为了达到减小爆破振动危害效应，实现安全施工的目的，从爆破机理的差分原理可知，炸药需均匀布置在爆破岩体中，避免爆破能量集中，以控制最大振动幅度。具体措施有：特殊位置可以采用炮孔间隔装药；避免炮孔超深；爆破炮泥堵塞实现交错装药；炮孔布置小排距，大孔距；防止炮孔密集参数小于1。

(5) 切断传播路径，控制传播过程

通过切断振动传播路径，可以达到降低振动幅度的效果。为尽量减少大前石岭隧道爆破施工过程振动效应对周围环境的危害，采取设置减振沟及减振孔作为爆破振动传播过程的减弱措施。在需要保护的建筑物与大前石岭隧道之间开挖一条深度大于建筑物地基深度的沟槽，形成一道屏障以阻止振动向建筑物传播。

5 结论

鉴于以往研究，很少考虑到自由面对爆破振速衰减的影响，而自由面面积大小影响着爆破效果。该文采用Ansys/LS-DYNA软件建模分析自由面面积对爆破振速衰减的影响，引入自由面面积参数改进爆破振速预测公式，总结爆破振速衰减规律，以大前石岭隧道为例，通过现场爆破振动监测试验数据验证预测公式的合理性，提出爆破振动安全距离计算公式和控制措施。得到以下结论：

(1) 隧道爆破振速衰减规律满足改进的萨道夫斯基公式。其中引入自由面面积参数，表明自由面面积越小造成质点峰值振速越大，振动越强烈。

(2) 通过爆破振速衰减规律可推导安全距离计算公式。以隧道爆破自由面面积平均值计算，该隧道爆破振动安全距离为191.76 m。

(3) 由经验公式可知，从增大爆破自由面面积、控制爆破炸药量、选择低爆速炸药、合理布置网孔和压制爆破振动波传播等方面可有效降低爆破振动负面危害。提出的相应的爆破振动控制措施，对隧道爆破安全施工具有指导意义。