支架现浇系杆拱桥吊杆张拉方案优化

周小勇， 吕志敏， 王加辉， 李庆刚

(1.中国地质大学(武汉)工程学院， 湖北 武汉 430074； 2.中交第二公路勘察设计研究院有限公司， 湖北 武汉 430056)

钢管混凝土系杆拱桥运用广泛，系梁(主纵梁)可承受拱脚水平推力，适用于各种地质条件，这种拱桥为外部静定、内部超静定体系[1]。施工中，吊杆的张拉顺序及索力会对结构内力分布及大小造成不同程度的影响[2]。此外有研究表明：实际工程中结构受力的最不利状态不一定出现在运营阶段，起控制作用的力学状态往往出现在施工过程中[3]。吊杆的安装与张拉是系杆拱桥施工过程中的关键环节，不合理的吊杆张拉方案造成的局部应力过大会给施工带来安全隐患，进而影响成桥后结构的安全[4]。

基于此，该文结合工程实例，提出7种不同的支架现浇系杆拱桥的吊杆张拉方案，并引入“峰态系数”评价指标定量评估方案优劣，通过对比分析结构在施工过程中及成桥后的内力状态，以期得到一个相对最优的吊杆张拉方案和施工索力。

1 工程实例

1.1 工程概况

江西安福县泸水河大桥位于城北西片区，上部采用中承式系杆拱结构，主桥全长156 m，跨径组合为(28+100+28) m，桥型总体布置如图1所示。

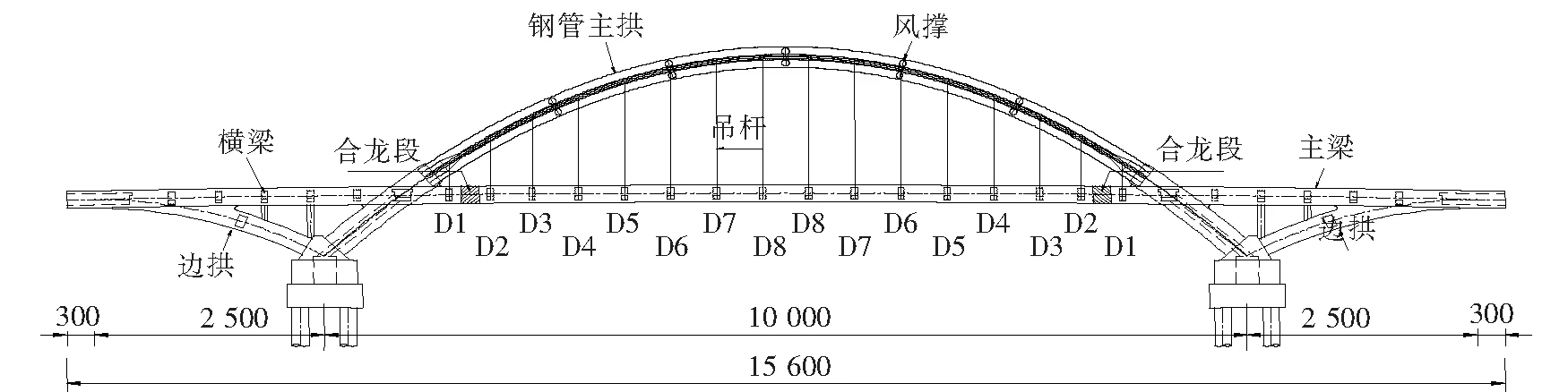
图1 泸水河大桥主桥桥型布置图(单位：cm)

上拱肋采用钢管混凝土，下拱肋采用钢筋混凝土，主拱采用Q345qD钢，管内C50补偿收缩混凝土，桥面以上为哑铃形断面，桥面以下为矩形实心断面，边拱肋高2.2 m，主拱肋高3.0 m，宽度均为1.8 m。系梁为矩形断面，采用C55预应力混凝土结构，高为2.2 m，宽为2.0 m。吊杆均采用37φ15.2 mm钢绞线整束挤压吊杆，间距为4.5～5.0 m，共32根(16对)。

主梁、下拱圈、边拱圈采用支架法施工[5]，钢管拱圈采用预制拼装法施工，施工流程如下：① 基础、桥墩、承台施工；② 支架现浇边拱肋；③ 中跨支架现浇主梁及横系梁；④ 支架对称安装拱肋、风撑；⑤ 安装吊杆，对称灌注管内混凝土；⑥ 拆除主拱肋支架，按要求顺序及索力张拉吊杆；⑦ 吊装桥面板梁，拆除所有支架；⑧ 施工桥面系，二次张拉吊杆。

1.2 全桥有限元模型

采用Midas/Civil建立全桥有限元模型(图2)，按施工流程进行施工阶段仿真模拟。模型如图2所示，全桥共计2 522个单元，2 514个节点。

图2 泸水河大桥主桥有限元模型

钢管拱肋采用施工联合截面模拟，吊杆采用仅受拉的桁架单元模拟，系梁、混凝土拱肋、横梁及下部结构均采用梁单元模拟，支架体系采用仅受压的弹性连接模拟，桩土截面采用土弹簧模拟。

泸水河大桥的边界条件及体系转化流程如图3所示。

图3 边界条件及体系转化流程图

由图3可知：大桥除了在合龙阶段存在体系转变外，其余施工阶段均保证结构为静定体系。

2 吊杆张拉方案

2.1 吊杆张拉顺序

钢管拱桥当采用悬臂法施工时，吊索一般由拱脚向跨中依次顺序张拉施工，但该桥采用支架法现浇施工主梁，吊索张拉顺序则可依据主拱和主梁的内力、变形情况、施工便利性等综合选取。吊杆张拉方案主要由两大因素组成，即张拉顺序和张拉控制力[6]。为确定该类型桥梁的合理吊杆张拉方案，该文提出7种吊杆张拉施工方案，吊杆编号见图1，约定横桥向相同编号的吊杆同时施工，具体张拉顺序如表1所示。

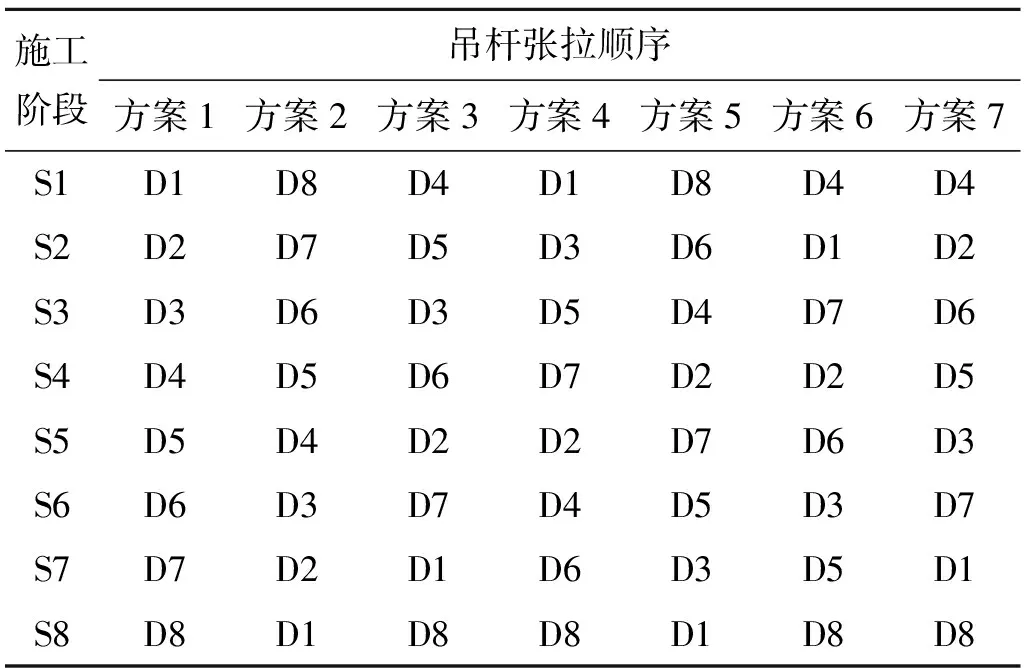
表1 不同方案下的吊杆张拉顺序

2.2 吊杆张拉控制力计算

成桥索力是一个目标索力，是确定吊杆张拉控制力的前提，当吊杆施工顺序确定，应计算对应的各吊杆张拉控制力，以确保在成桥阶段，吊杆索力均能达到目标索力。

合理成桥状态的确定方法通常有以下几种：无约束的索力优化、有约束的索力优化和影响矩阵法[7-8]。其中，影响矩阵法多用于二次调索，无约束索力优化法具代表性的有最小弯曲能量法和弯矩最小法，该文采用最小弯曲能量法确定成桥索力。最小弯曲能量法是通过对吊杆索力的调整，使结构的弯曲应变能最小，这时吊杆索力即合理成桥状态下的目标索力。Midas/Civil实现方式如下：将系梁、主拱、吊杆的轴向刚度放大(通常放大104倍)，进行一次成桥计算，此时的吊杆索力值即所求的目标索力。

目标索力值确定后，求解施工索力时可采用倒拆法和正装迭代法。倒拆法思路简单，无法考虑时间参数，不能计算材料的时间效应如收缩徐变等，但只需一次计算即可完成；正装法需要迭代，计算代价大，结果相对可靠，该文采用正装迭代法确定各方案的施工索力，其基本思路为：先假定一组施工索力，通常采用目标索力作为初值进行正装计算，得到第一组成桥索力，将该成桥索力与目标索力进行比较求差，再将差值补偿给上一次的迭代初值，补偿后的吊杆索力作为下一次正装计算的施工索力，重复迭代多次，直至前后两次索力差满足预定收敛条件。

3 结果与分析

3.1 吊杆张拉控制力

根据最小弯曲能量法和正装迭代法求得的目标吊杆索力和吊杆张拉控制力见表2。

表2 不同张拉方案下的吊杆张拉控制力

由表2可知：

(1) 即使目标索力相同，不同的吊杆张拉方案，吊杆施工索力存在较大差异。如方案1和方案3中的吊杆D1，在目标索力均为970 kN的情况下，吊杆张拉控制力分别为1 105、870 kN。

(2) 方案1(从拱脚至跨中对称依次张拉吊杆)的吊杆施工索力变化较大(最大1 105 kN，最小560 kN，平均790 kN)，而方案2(从拱顶至拱脚对称依次张拉吊杆)的吊杆张拉控制力相对均匀(最大915 kN，最小735 kN，平均860 kN)，可使吊杆张拉设备的规格和吊索型号相对统一。对称间隔张拉和对称交替张拉方案的规律与对称依次张拉方案一致，即从拱顶至拱脚张拉吊杆方案的吊杆张拉控制力更为均匀。

(3) 对比依次张拉吊杆(方案1～3)和间隔张拉吊杆(方案4～7)可以看出：间隔张拉吊杆方案中的吊杆张拉控制力更为离散，结合吊杆张拉顺序，间隔张拉吊杆方案的施工便利性不如依次张拉吊杆方案。

3.2 施工过程结构内力

桥梁采用支架法施工，系梁支架在吊杆张拉完毕后拆除，在吊杆张拉过程中，系梁的内力及位移变化并不明显，而对主拱内力影响较大，因此该文仅针对钢管拱肋在施工过程中的内力进行对比分析。

3.2.1 钢管拱肋内力包络

各施工方案中，钢管拱肋纵桥向出现的最大、最小弯矩包络如图4、5所示。

图4 钢管拱肋最大弯矩包络图

图5 钢管拱肋最小弯矩包络图

由图4、5可得：

(1) 对称依次张拉吊杆容易造成局部内力偏大，从拱脚至拱顶依次张拉(方案1)易造成拱脚上缘拉应力偏大(方案1拱脚位置处最小弯矩为-10 365.96 kN·m);从拱顶至拱脚依次张拉(方案2)易造成拱顶下缘拉应力偏大(方案3拱顶位置处最大弯矩为5 635.99 kN·m)；从1/4拱肋处至拱脚、拱顶对称依次张拉(方案3)易造成1/4拱肋处下缘拉应力偏大(方案2中1/4拱肋处最大弯矩为4 771.06 kN·m)。

(2) 对称间隔张拉吊杆方案与依次张拉方案对比，间隔张拉吊杆造成的局部位置内力要小于依次张拉吊杆方案。例如从拱脚至拱顶间隔张拉(方案4)与依次张拉(方案1)在拱脚位置处产生的最大弯矩分别为-8 313.95 kN·m和-10 365.96 kN·m。这表明间隔张拉吊杆要优于依次张拉吊杆。

(3) 对比7种不同吊杆张拉方案下的拱肋最大弯矩包络图，从1/4拱肋处开始张拉吊杆要优于其余两种方式(从拱脚开始张拉和从拱顶开始张拉)，尤其是在方案7的吊杆张拉顺序下，钢管拱肋产生的最大、最小弯矩更为平稳和均匀。

3.2.2 钢管拱肋关键截面位置内力变化

取拱脚、1/4拱肋和拱顶3个关键截面处的结构内力变化进行分析，7种不同方案下关键截面处的内力变化情况如图6～8所示。引入峰态系数K，定量评价不同吊杆张拉方案施工过程中结构内力的均匀程度(峰态系数越大，代表结构内力分布越不均匀，反之亦然)。峰态系数K的定义如下：

(1)

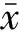
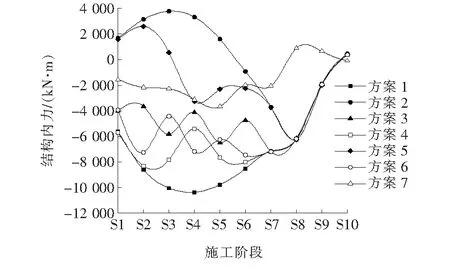
图6 拱脚处结构内力变化图

图7 拱顶处结构内力变化图

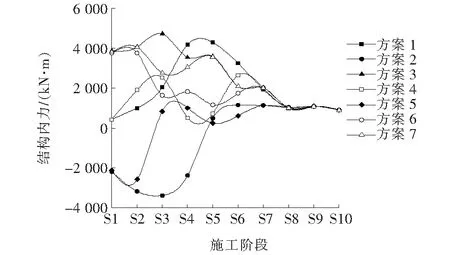
图8 1/4拱肋处结构内力变化图

不同方案下的峰态系数变化如图9所示。

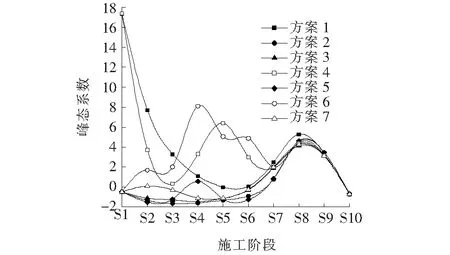
图9 各方案峰态系数变化图

图6～9中施工阶段S1～S8分别为张拉吊杆的各个阶段，S9和S10分别为拆除系梁支架阶段和考虑收缩徐变的成桥阶段。由图6～9可知：

(1) 吊杆张拉方案存在“收敛性”，成桥状态确定后，张拉顺序不会影响成桥内力，各方案最后一根吊杆张拉后，全桥的内力状态会趋于一致。但不同张拉方案下的吊杆张拉力相差达23%，如方案4和方案7的D1吊杆张拉力。

(2) 依次张拉吊杆方案(方案1～3)下的结构内力变化呈现“持续性”的特点，间隔张拉方案则呈现“往返性”的特点。如方案1(从拱脚至拱顶依次张拉吊杆)拱脚位置处的弯矩，从S1阶段的-5 597.18 kN·m持续增大到S4阶段的-10 365.96 kN·m，再持续减小至目标状态，这样的变化方式显然对结构不利。

(3) 间隔张拉吊杆方案较依次张拉吊杆，在施工过程中的结构内力更为均匀。特别是方案7，在拱脚截面和1/4拱肋截面、拱顶截面处的内力变化幅度小，没有突变，且钢管拱肋的内力分布也较均匀。方案7的钢管拱肋内力峰态系数在S1～S6阶段的变化为-1.13～0.10。

3.2.3 钢管拱肋关键截面位置应力变化

同结构内力分析一样，取拱脚、1/4拱肋和拱顶3个关键截面处的钢管应力变化作分析，不同方案下的截面应力变化如图10～12所示。此外，各方案下峰态系数变化如图13所示。

图10 拱脚处结构应力变化图

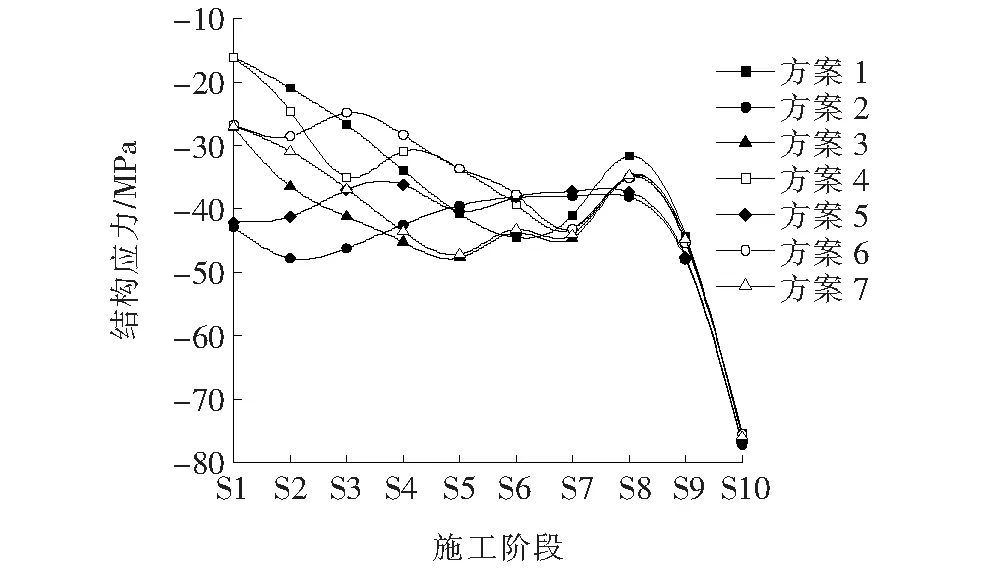
图11 拱顶处结构应力变化图

由图10～13的结果可知：

(1) 同结构弯矩变化类似，拱肋应力变化也呈现出“收敛性”，即当成桥状态确定后，吊杆的张拉顺序并不影响成桥的结构应力，在张拉完最后一根吊杆时，拱肋结构应力趋于一致。

(2) 拱肋应力区别较大出现在张拉前几根吊杆，从拱顶至拱脚张拉吊杆造成的拱顶应力大于其他方案(方案2 S1阶段在拱顶处的应力为-42.85 MPa)，从1/4拱肋处至拱脚、拱顶对称依次张拉吊杆易造成1/4拱肋处及拱脚处应力大于其他方案(方案3 S1阶段在1/4拱肋及拱脚处的应力分别为-35.7 MPa和-38.5 MPa)。

图12 1/4拱肋处结构应力变化图

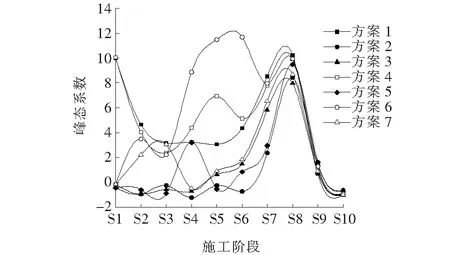
图13 各方案峰态系数变化图

(3) 结合结构应力变化图及峰态系数变化图可以发现，从拱顶至拱脚张拉吊杆与从1/4拱肋处张拉吊杆造成的结构应力分布更为均匀(方案2的钢管拱肋内力峰态系数在S1～S6阶段为-1.20～0.41，方案3钢管拱肋内力峰态系数在S1～S6阶段为1.48～-0.13)。同时，就方案7而言，关键截面位置处结构应力差别不大，分布也较为均匀且没有较大突变(方案7钢管拱肋内力峰态系数在S1～S6阶段为3.06～-0.48)。

4 结论

以钢管混凝土系杆拱桥为研究对象，结合具体工程实例，提出7种不同吊杆张拉方案，对比分析每种张拉方案下的吊杆张拉控制力及施工阶段结构内力，得到以下结论：

(1) 不同吊杆张拉方案存在“收敛性”，即当目标成桥状态确定，用对应的施工索力进行张拉，张拉顺序不影响成桥内力，但不同方案的吊杆张拉力相差较大。

(2) 从施工便利性分析，对称依次张拉吊杆方案要优于对称间隔张拉，其中，拱顶至拱脚依次张拉吊杆，不需要来回挪动张拉设备，吊杆张拉控制力也相对均匀。

(3) 从结构受力分析，对称依次张拉吊杆易造成局部位置处(拱脚、拱顶、1/4拱肋)内力偏大，从拱脚至拱顶依次张拉吊杆易造成拱脚处内力偏大，对称间隔张拉吊杆会使结构受力稍有改善，但整体趋势不变。

(4) 从内力分布来分析，间隔张拉吊杆方案较依次张拉吊杆产生的结构内力更均匀，特别是对称交替张拉吊杆方案下，施工过程中结构内力分布均匀，没有产生较大突变，有利于结构受力和施工状态下的桥梁安全性。