地基路基路面协同沉降变形一体化设计方法研究

2022-05-13裘友强宫玉明刘军勇

中外公路 2022年2期

裘友强，宫玉明，刘军勇

(中交第一公路勘察设计研究院有限公司，陕西西安 710075)

1 引言

作为道路结构层的3个主要组成部分，地基、路基和路面是密不可分的一个共同受力体，作用在路面上的车辆荷载会依次通过路面、路基向下传递到地基上，同样地基的沉降变形也会通过路堤、路面向上传递而影响到车辆的正常行驶。大量的工程实践和监测资料也表明，修建在地基上的路基路面，会由于地基的不均匀沉降在路面结构内部产生附加应力，不均匀沉降值越大，其产生的附加应力也会越大，当不均匀沉降产生的附加应力与路面荷载应力叠加超过路面结构容许应力时，路面结构将发生破坏，从而影响道路的正常使用[1-2]。

关于公路地基路基路面协同作用方面的研究，目前国内外许多学者主要集中在地基变形对路基变形的影响，或者研究路基变形对路面结构应力的影响。卢正等[3]结合现有规范关于路面弯沉控制的思想，考虑路面路基的相互作用及协调变形，提出了路基顶面的动变形控制标准和确定方法；姬杨蓓蓓等[4]通过建立路基发生融沉变形时沥青路面结构的轴对称计算模型，分析了融沉变形对最大拉应力点位的影响，探讨了融沉盆形状、半径、融沉深度等因素对沥青路面结构面层和基层最大拉应力的影响；周虎鑫等[5]从公路路面功能性指标、结构性指标两个方面，提出了在软土地基上修筑高等级公路路面容许不均匀沉降指标。

从研究现状来看，在分析地基沉降变形对路面结构影响时，忽略了路基作为中间结构的影响，即未将地基、路基与路面作为一个整体考虑。此外，现行的路基路面设计方法中并没有将地基所引起的工后沉降这一因素考虑进去，地基、路基与路面设计上相互独立，路面的设计仅仅从路面本身考虑，路面的破坏往往归咎于路面荷载或路基上部，这在地基-路基-路面一体化设计方面是一个重大的缺陷。

鉴于此，该文依托青海省察格高速公路察尔汗盐湖湖心区域盐渍土地基处治试验段，基于数值模拟与现场不均匀沉降监测结果，采用两种路面结构层不均匀沉降的施加方法，将地基、路堤、路面三者有机结合起来，分析地基、路基协同沉降变形下路面结构层的应力响应，提出满足路面结构性、功能性要求的路基、地基沉降控制标准和计算方法。

2 地基路基路面协同变形数值模型

2.1 计算模型设计

为避免模型边界效应，地基计算宽度取路基基底宽度的5倍，地基计算深度≥20.5 m，地基土渗透系数取1 m/d。其中，路面厚度设置为0.7 m，边坡坡率为1∶1.5。此外，计算模型中风积沙隔断层厚度取0.8 m，砾石隔断层厚度取0.4 m。除将路面视为线弹性体外，地基、路基及风积沙、砾石隔断层均视为弹塑性体，采用Mohr-Coulomb屈服准则计算，计算模型如图1所示。

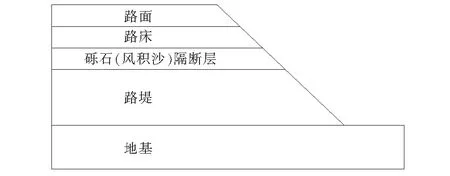
图1 地基、路基和路面协同变形计算模型

2.2 计算模型参数

根据依托工程地勘土工试验数据，并结合现场试验结果，确定地基、路基(含隔断层)、路面等结构层计算参数，如表1所示。

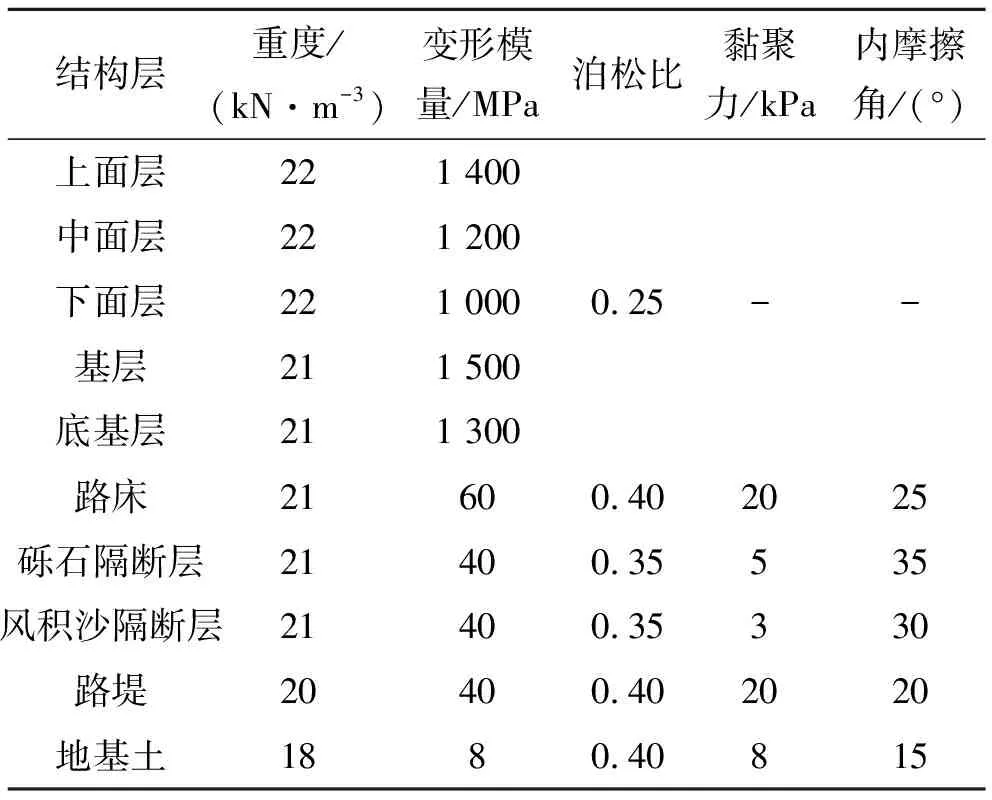
表1 各结构层计算参数

2.3 计算模型基本假定与边界条件

(1) 材料的本构模型：路面各结构层为连续均质、各向同性的线弹性材料，力学特性采用弹性模量和泊松比表征；地基、路堤、隔断层与路床视为弹塑性体，假定服从Mohr-Coulomb屈服准则。

(2) 同层材料视为各向同性且连续，各结构层之间为完全连续，沉降变形过程中，层间不发生脱空。

(3) 路面各结构层在垂直方向完全连续，路面各结构层在行车荷载与不均匀沉降作用下产生竖向变形，层间不出现脱空现象。

(4) 路面结构层与路床之间的接触面，考虑路床对路面结构变形的水平向约束，水平位移连续，水平变形过程中不发生脱离。

(5) 底基层与路床(路基)之间为完全接触条件；底基层与路床(路基)顶面的竖向应力和竖向位移连续，即当路堤发生沉降后，路面结构层会随之下沉，相互间变形协调。

(6) 路堤为分层填筑，分层厚度为0.3～0.4 m。为使地基充分排水固结，每填筑3层路基，设置停工期：在路基高度h≤3.0 m时，填筑施工和停工固结时间均为30 d；填筑高度h>3 m时，为保证地基充分固结和路基稳定，填筑施工和停工固结时间均为60 d。公路设计服役期为15年。

(7) 地下水位为零水位，地表为自由排水边界。考虑路基、路面填筑施工期和运营期地基固结沉降过程。

(8) 约束模型左、右两边水平位移，约束模型底边的水平和竖向位移。

3 地基路基协同变形下路面应力计算

路基的不均匀沉降主要是在路基自重作用下，地基渗流固结引起。路基中心处的沉降量将大于路基外缘的沉降量，不均匀沉降呈盆状。目前，研究路面结构层层底应力通常采用的方法是给定路面结构层层底(路床顶面)拟定的不均匀沉降曲线或在路面施加车辆荷载从而计算路面各结构层沉降变形和层底应力，但施加拟定的路面或路基不均匀沉降与实际沉降不符。

针对此现状，为了分析地基、路基协同变形对路面结构层应力的影响，从公路地基、路基与路面协同变形实际情况出发，对于路面结构层层底沉降将采用两种方法进行施加：① 考虑地基、路基与路面协同沉降变形，由地基固结沉降计算出路床顶部的沉降，并将沉降曲线施加于路面结构层层底，这种方法与地基、路基、路面协同沉降实际情况一致；② 根据依托工程路面结构层实测沉降曲线，将实测沉降曲线代入路面结构模型进行应力计算分析。

3.1 凹曲线不均匀沉降的施加

针对第一种不均匀沉降施加方法，为与现场实测的整个路基横断面不均匀沉降曲线相对应，建立路面结构计算模型时采用路面全宽度模型，计算简图见图2。

路床顶面沉降曲线拟合方程为：

s=A|x|2+B|x|+C

(1)

图2 地基、路基协同变形下路面结构层应力计算简图

式中：s为路基横断面方向上地基沉降(或路基沉降)；x为路基横断面上点距路基中心距离；A、B、C分别为方程的拟合参数。

考虑不同路基高度和不同路基宽度两种工况下路基沉降曲线的施加，采用式(1)对路基横断面沉降曲线进行拟合，拟合参数结果见表2。

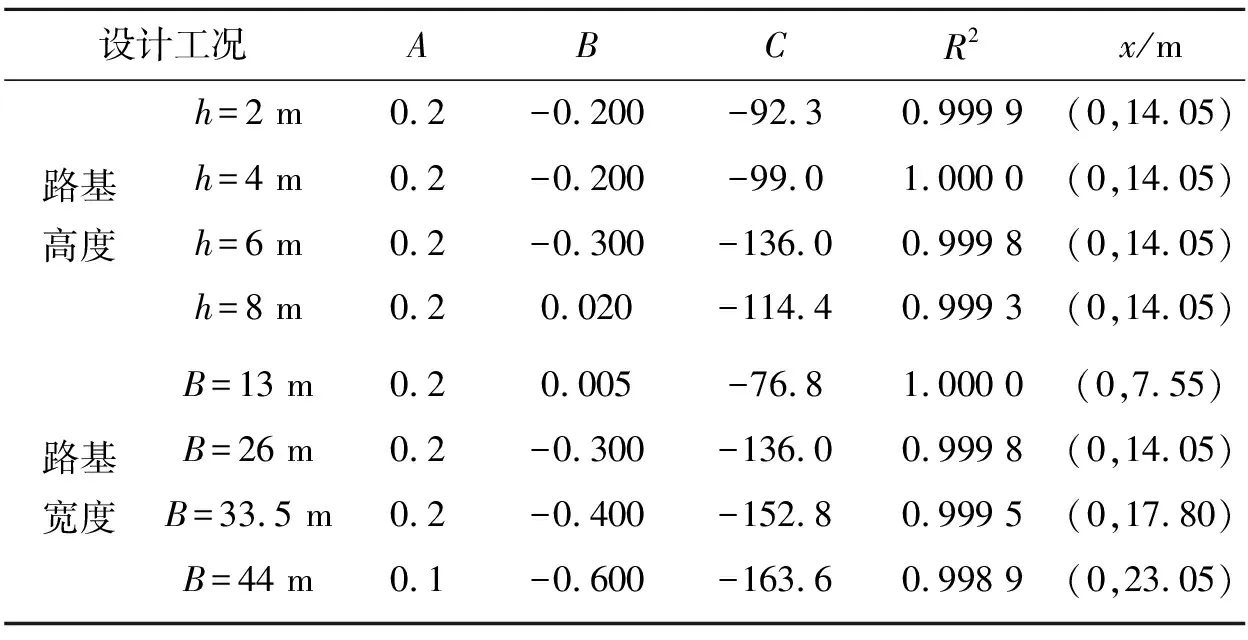
表2 不均匀沉降凹曲线参数

3.2 凸曲线不均匀沉降的施加

针对第二种不均匀沉降施加方法，对依托工程10余处路基横断面进行沉降监测，监测点分别位于左、右路肩和路中心，监测周期为3～42个月不等；同样采用拟合方程s=A|x|2+B|x|+C，对路基横断面沉降曲线进行拟合，拟合参数结果见表3。

表3 不均匀沉降凸曲线参数

3.3 地基路基协同沉降变形下路面应力响应

基于上述两种不均匀沉降施加方法，结合凹曲线和凸曲线拟合参数计算结果，对地基、路基协同沉降变形下路面结构层应力进行计算，计算结果见表4、5。

从表4、5可以看出：不同形式的沉降曲线对路面结构层应力分布及大小有着重要的影响：凹曲线沉降在路面结构层面层中产生压应力，压应力位于面层底部；基层和底基层底部产生拉应力，路面应力控制层为基层和底基层。而对于凸曲线沉降而言，其在路面结构层面层中产生拉应力，最大拉应力位于上面层和中面层顶面，路面应力控制层为上面层和中面层；基层和底基层产生压应力，压应力位于基层和底基层底部，在部分基层和底基层顶面也存在较小的拉应力。

4 协同沉降控制限值计算方法

4.1 满足路面结构性要求的差异沉降标准

对不同差异沉降和沉降变坡率的路面结构层层底应力进行验算，确定满足路面结构性要求的路基顶面沉降控制指标。路基差异沉降与沉降变坡率满足：

max|δij|=|si-sj|≤|δ|av

(2)

Δi=|δij|/Lij=|si-sj|/Lij≤Δiav

(3)

式中：δij为路中心与路肩的最大差异沉降量；si为路基顶面横断面路中心沉降量；sj为路肩沉降量；|δ|av为路基差异沉降容许值；Lij为路基(路床顶面)宽度的一半；Δiav为路基横坡沉降变坡率容许值。

不同沉降曲线情况下，拟合关系式分别为：

凹曲线：Δiav=0.011B+0.098 7

(4)

凸曲线：Δiav=0.020 5B+0.008 3

(5)

不同路面宽度、不同差异沉降曲线情况下，路基横向差异沉降容许值和沉降变坡率容许值见表6。

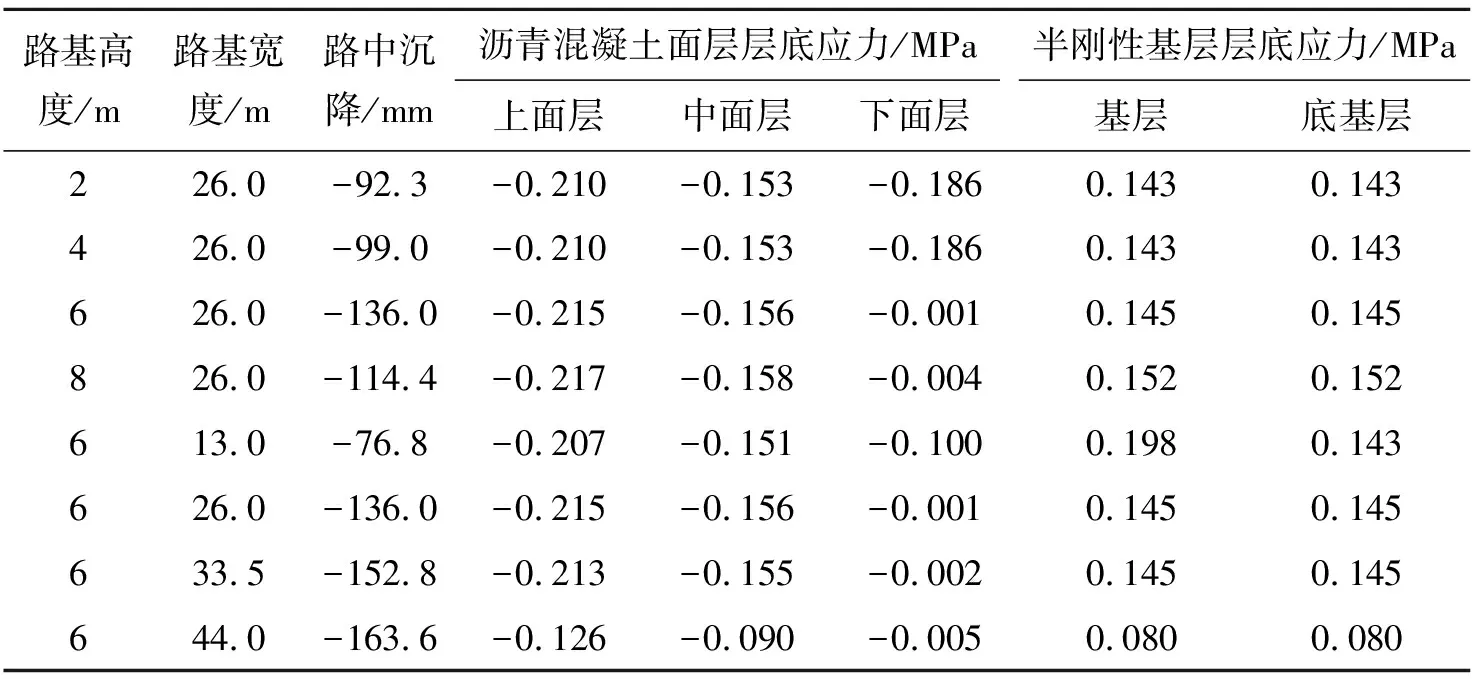
表4 路面结构层层底应力计算结果(计算沉降曲线)

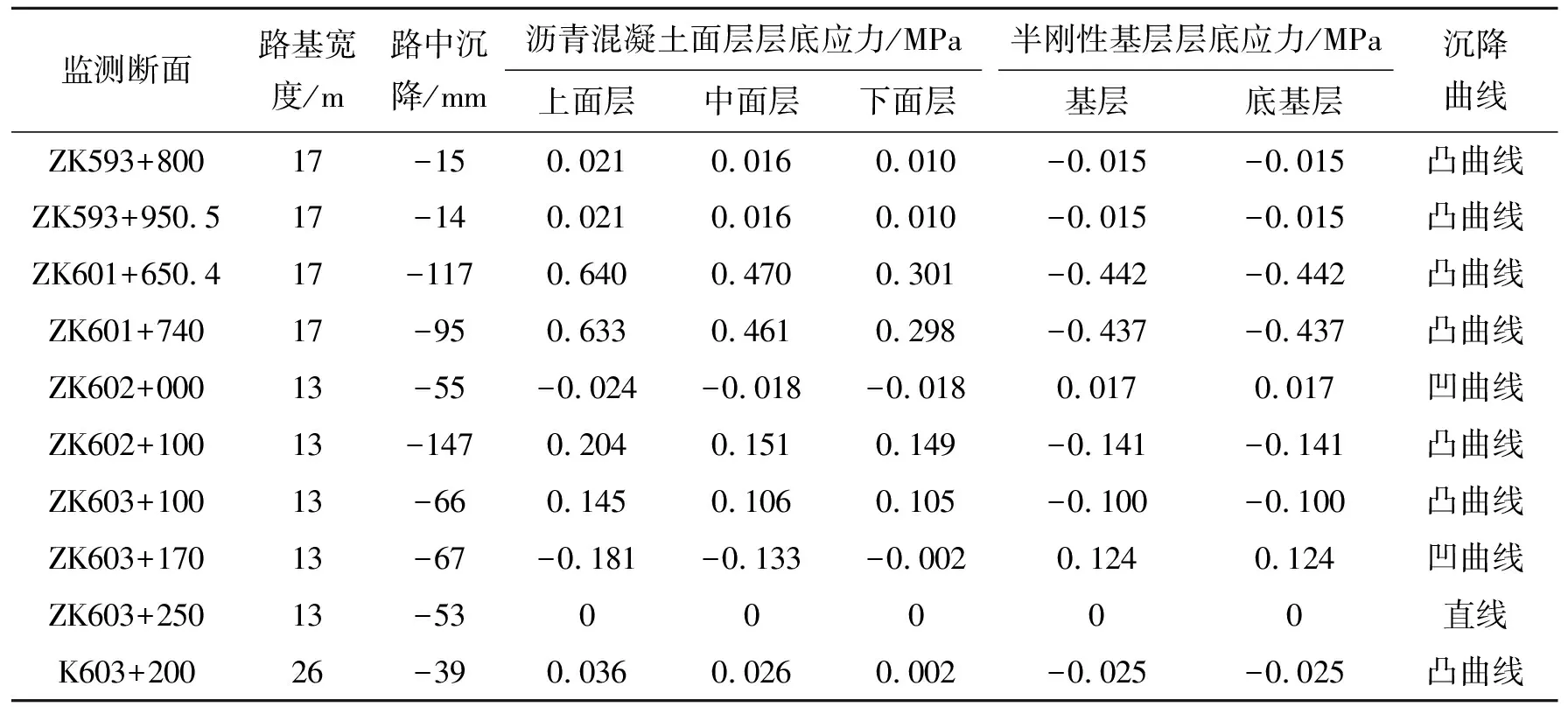
表5 路面结构层层底应力计算结果(实测沉降曲线)

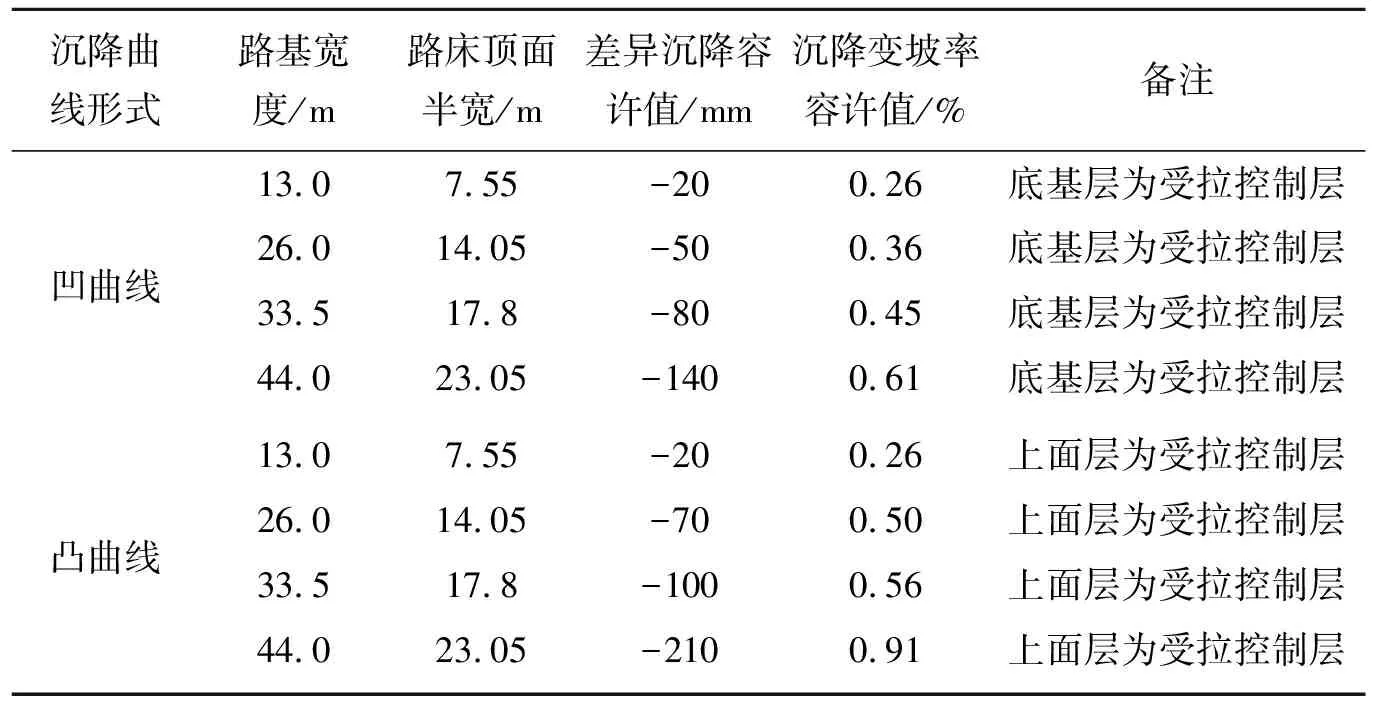
表6 路基横向差异沉降和沉降变坡率容许值

4.2 满足路面功能要求的差异沉降指标

设计路面横坡的目的是及时将降雨排出路面，并给车辆提供足够的行车向心力，以保证行车安全。路基的不均匀沉降主要是由路基自重以及左右幅地基的工程地质局部差异、地基处理、施工因素等所引起，路基中心处的沉降量将大于或小于路基边缘的沉降量，不均匀沉降基本上呈下凹盆状或上凸抛物线形。因此，工程实际中路基路拱坡度应尽可能地采用较大值，目前的工程实践中一般采用路拱横坡的高限2%，待路基沉降稳定后，又不得低于下限1%，否则会引起排水不畅、不利于行车安全[6-8]。

综上所述，路基横向差异沉降应同时满足路面结构性要求和功能性要求，由表6可以看出：计算结果可作为路基差异沉降控制标准。

4.3 路基与地基沉降控制限制计算方法

(1) 一般路段路基与地基沉降标准

为综合考虑各因素对路面结构层附加应力的影响，采用差异沉降量|δij|和横坡变坡率Δi作为沉降主要控制因素。根据上述分析得到的地基、路基协同沉降变形条件下满足路面结构性、功能性要求的路基横向差异沉降容许值和沉降变坡率容许值，进一步推导路基、地基容许沉降量，表达式如下：

Δi=|δij|/Lij=|si-sj|/Lij≤Δiav

(6)

式中：si为路面填筑完成后路基顶面路中心总沉降量；sj为路面填筑完成后路基顶面路肩处总沉降量，路基顶面路中心和路肩处总沉降量可由计算或实测值预测得出。

对于相同的路基高度或路基宽度，同一横断面上各点路基沉降与地基沉降的比值基本相同，即路基与地基沉降比a可视为一定值。设r为路肩处地基沉降量与路中心地基沉降量的比值，即：

sj地/si地=r

(7)

si=si地·a

(8)

sj=sj地·a=si地·r·a

(9)

si-sj=si地·a·(1-r)≤Lij·Δiav

(10)

由于si地·a=si，则可推出：

(11)

(12)

式中：si地为路中心地基沉降量；sj地为路肩处地基沉降量；siav为路基顶面中心处容许沉降量；si地av为路中心处地基容许沉降量，其他参数意义同前。

(2) 公路纵向路基与地基沉降标准

无论是路基横向还是纵向，沥青路面结构层容许拉应力技术指标要求是相同的。因此，公路纵向路基与地基容许沉降计算方法同上，区别仅为根据计算或实测资料，分析公路纵向路基、地基沉降曲线，找出相邻最大沉降量断面(点)A处沉降si、si地和最小沉降量断面(点)B处沉降sj、sj地，A、B两点沿公路纵向连线(路基顶面)即为Lij，同法可计算出公路纵向路基与地基沉降容许值。公路纵向路基和地基不均匀沉降将改变公路纵坡，其改变后的纵坡值应同时满足相应公路等级(设计时速)的最大纵坡要求。路基沉降容许值siav和地基沉降容许值si地av取横向和纵向计算结果两者中较小值。