基于ARIMA和SVM模型的沥青路面使用性能预测比较
2022-05-13张丽娟杨源梅诚许薛军
张丽娟, 杨源, 梅诚, 许薛军
(1.华南理工大学 土木与交通学院, 广东 广州 510640; 2.广东省交通运输规划研究中心, 广东 广州 510101)
随着行车荷载急速增长和使用年限不断增加,沥青路面的损坏愈来愈严重,准确预测和评价沥青路面使用性能衰变趋势,是判断养护时机、制定养护规划的前提[1]。目前中国公路管理部门构建了多个公路养护信息管理平台,进一步完善了中国公路基础数据库,应利用大数据理论及技术对这些数据进行挖掘分析,建立有效的沥青路面使用性能预测模型,可为科学制定路面养护管理决策提供理论支撑。
路面使用性能数据是定期检测所获取的按时间先后顺序排列所形成的时间序列,通过曲线拟合和参数估计建立时间序列模型,可以定量分析和预测路面使用性能发展趋势。武建民等[2]、法鲁克·铁来克[3]分别采用基于时间序列分析法的ARIMA模型对路面行驶使用性能指数RQI、沥青路面损坏状况指数PCI进行预测,发现ARIMA模型预测精度在5%以内,预测精度较高。
沥青路面使用性能受自然环境、交通荷载、结构、材料、维修养护等多种非线性因素综合影响。支持向量机(SVM)是在处理小样本非线性问题方面具有特有优势的一种机器学习算法,SVM算法所采用的核函数及其参数直接影响到回归预测精度[4]。黄冰等[5]采用多项式核函数建立了路面破损状况PCI的SVM预测模型;刘黔会等[6]利用径向基核函数建立沥青路面使用性能的SVM预测模型;董锴等[7]建立采取径向基核函数的SVM路面评价模型进行路面性能综合评价。
针对沥青路面使用性能具有样本小、维数高与非线性等特点,有学者将SVM和其他方法相结合以提高SVM预测精度。李巧茹等[8]结合主成分分析法和支持向量机理论,建立了PCA-SVM沥青路面使用性能评价模型;李海莲等[9]构建了改进萤火虫算法和支持向量机相结合的IFA-SVM预测模型;赵静等[10]提出了基于灰色关联度分析和支持向量机回归(GRA-SVR)的沥青路面使用性能预测模型。
时间序列模型和支持向量机模型预测技术各有其特点,应根据路面性能变化规律采用适宜的沥青路面性能预测模型。杨彦海等[11]分别利用BP神经网络时间序列模型和支持向量机模型对就地热再生沥青路面中沥青老化指标衰变进行预测,发现在有限数据量情况下支持向量机模型较BP神经网络时间序列模型的预测精度高。
该文分别构建时间序列ARIMA和支持向量机(SVM)模型,且SVM模型分别采用线性核、多项式核、径向基核和Sigmoid核4种核函数对沥青路面的PCI值进行预测,对比分析ARIMA和SVM模型及SVM模型所采用不同核函数的预测结果,并将所选择的预测模型应用于广东省普通国省道沥青路面使用性能预测中。
1 ARIMA和SVM模型预测原理
1.1 ARIMA模型预测原理
差分自回归移动平均模型(ARIMA模型)是最常用的一种时间序列分析法模型。ARIMA(p,d,q)模型中,AR、MA分别为自回归模型、移动平均模型,p、q为相应的自回归模型阶数、移动平均模型阶数,d为将非平稳时间序列进行平稳化处理的差分阶数。ARIMA模型是差分运算和ARMA模型的结合,其用一定的数学模型来近似描述预测对象随时间变化又相互关联的数据序列,模型检验合理后,就可以通过时间序列的过去值和现在值来预测未来某时段的值。
设{xt,t∈T}为时间序列,B为后移算子,即Bxt=xt-1,则ARIMA(p,d,q)模型可表示为[2,12]:
Φp(B)(1-B)dxt=θq(B)at
(1)
其中:
Φp(B)=1-Φ1B-Φ2B2-…-ΦpBp
(2)
θq(B)=1-θ1B-θ2B2-…-θqBq
(3)
式中:Φ和θ分别为自回归系数和移动平均系数;Φp(B)为自回归算子;θq(B)为移动平均算子;at为白噪声时间序列。
ARIMA模型的建模步骤一般为[13]:
(1) 时间序列平稳性检验。观察初始时间序列的线性趋势、周期性、方差齐性等特点,采用ADF检验方法,对初始时间序列进行单位根检验。将非平稳时间序列进行d阶差分处理为平稳时间序列。
(2) 对平稳时间序列进行模式识别,确定模型的阶数。采用自相关系数和偏自相关系数初步确定阶数p、q可能值,根据BIC准则(即BIC值越小越好)得到相对较优的阶数p和阶数q。
(3) 模型的检验。通过Q统计量检验残差是否为白噪声,判断预测模型的合理性。
(4) 模型预测。根据检验合理的ARIMA模型进行预测分析。
1.2 SVM模型预测原理
支持向量机(SVM)是一种通过有限的样本信息进行数据挖掘、建立逼近真实问题模型的机器学习算法,其在小样本、非线性、高维数的回归预测领域优势明显,有效地避免了过学习、欠学习等现象。
SVM将样本空间中的非线性数据通过内积核函数映射到高维特征空间,并在新的高维特征空间中构造回归函数f(x),从而实现样本空间中的非线性回归分析。
设样本集:(x1,y1),(x2,y2),…,(xl,yl),xi∈Rn为输入变量,yi∈R为输出值,R为实数集。寻求的支持向量机回归函数为[5,9]:
f(x)=ω·φ(x)+b
(4)
式中:ω为权重向量;b为偏置量;φ(x)为映射函数。
(5)
(6)

采用拉格朗日乘子法将式(5)的最优化问题转换成对偶问题进行求解,即:
(7)
(8)

引入核函数,得到变形后的回归函数方程为:
(9)
式中:K(xi,x)为核函数。
常用的满足Mercer条件的核函数有[4-5]:
(1) 线性(Linear)核函数:K(xi,x)=(xi·x)
(2) 多项式(Polynomial)核函数:
K(xi,x)=[γ(xi·x)+r]d
(3) 径向基(RBF)核函数:
K(xi,x)=exp(-γ‖xi-x‖2)
(4) Sigmoid核函数:
K(xi,x)=tanh[γ(xi·x)+r]
式中:γ、r、d为待定参数。
在支持向量机预测过程中,核函数和惩罚参数C的取值直接影响预测精度。支持向量机学习算法本质上是基于核函数的学习算法。
2 ARIMA模型和SVM模型预测PCI值对比
2.1 ARIMA模型预测PCI值
广东佛山一环北延线路段采用沥青路面结构,表1为该路段在2011—2015年的PCI、RQI、RDI(路面车辙深度指数)、SRI等沥青路面使用性能评价指标数据。
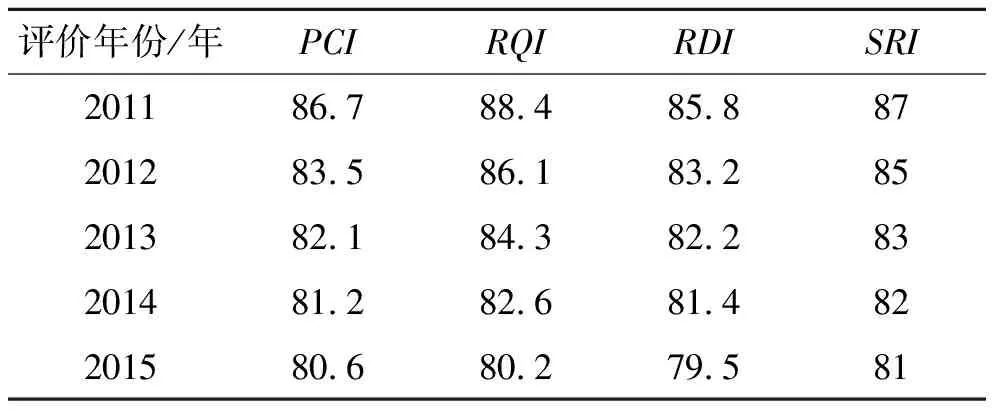
表1 佛山一环北延线路段路面使用性能评价数据
以表1中的PCI值预测对比分析ARIMA模型和SVM模型在沥青路面使用性能预测中的应用。
建立ARIMA模型进行数据分析时,需要通过调整模型参数以满足精度要求。针对表1的PCI指标数据,采用SPSS软件建立了ARIMA(1,0,1)模型,表2、3为模型拟合参数。
从表2、3可见:ARIMA(1,0,1)模型平稳的R2、R2分别为0.913和0.914,说明ARIMA(1,0,1)模型适用于拟合PCI数据序列,但均方根误差RMSE较大,说明ARIMA(1,0,1)模型的拟合精度不够高,且t统计(Sig.列)的显著性不明显。因此,需调整ARIMA(1,0,1)模型的移动平均数,将模型调整为ARIMA(1,0,0),表4、5为改进后的ARIMA(1,0,0)模型参数。

表2 ARIMA(1,0,1)模型拟合参数

表3 ARIMA(1,0,1)模型输出参数
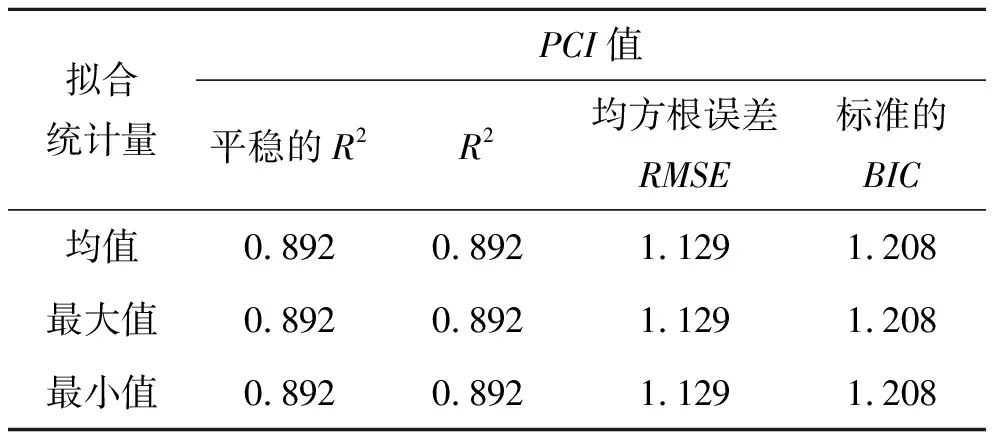
表4 ARIMA(1,0,0)模型拟合参数

表5 ARIMA(1,0,0)模型输出参数
从表4、5可以看出:ARIMA(1,0,0)模型保持了较大、较平稳的R2,均方根误差RMSE减小,模型拟合度高,且t统计(Sig.列)的显著性明显。ARIMA(1,0,0)模型的BIC值也较ARIMA(1,0,1)模型的BIC值小,一般而言,选取BIC值小的模型为最佳模型。因此,选用ARIMA(1,0,0)模型作为预测模型,佛山一环北延线沥青路面的PCI值预测结果如表6所示。
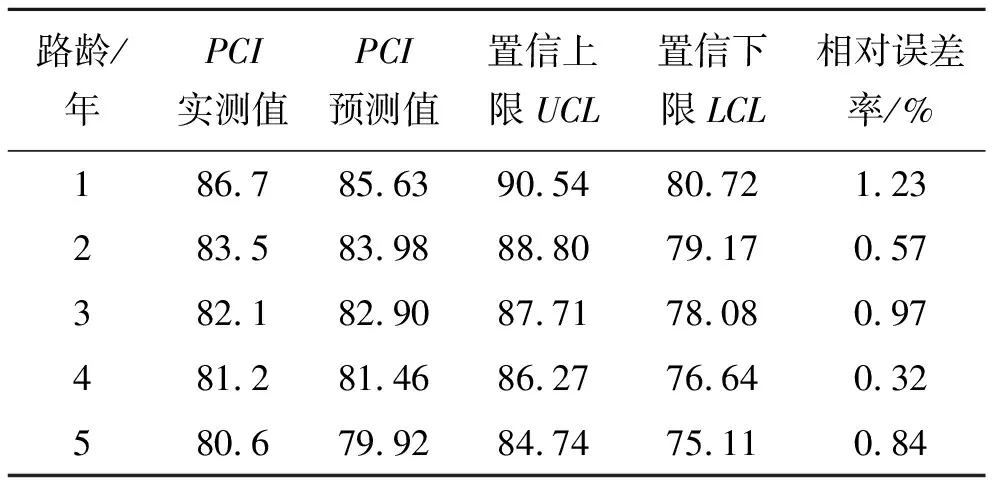
表6 ARIMA(1,0,0)模型PCI预测值及置信区间
从表6可见:ARIMA模型预测PCI值的精度比较高,相对误差率在1.23%以下。
2.2 SVM模型预测PCI值
以佛山一环北延线路段沥青路面结构的PCI指标数据(表1)为例,利用Matlab系统和libSVM软件包进行SVM回归预测仿真分析。核函数的选择是构造具有良好性能SVM模型的关键[4],通常可以利用专家的经验预先选定核函数;或从试用的不同核函数中选取误差最小的核函数作为最佳核函数,即Cross-Validation方法。
采用均方误差MSE和相关系数平方SCC指标来评价预测精度,从线性核函数、多项式核函数、径向基核函数和Sigmoid核函数中,通过Cross-Validation方法选取最优的核函数构建SVM预测模型。
表7、8为4种核函数的SVM模型PCI值预测结果及其精度评价。

表7 SVM模型PCI值预测结果

表8 SVM模型PCI值预测精度评价
从表7、8可以看出:选择不同核函数会产生不同的预测结果,核函数对预测结果影响显著。沥青路面使用性能是总体平稳、局部波动的序列,4种核函数中,多项式核函数预测的PCI值变化趋势与实测值最接近,预测效果最佳;径向基核函数预测结果与多项式核函数预测结果相近,预测结果较理想;线性核函数预测效果基本满足预测精度要求;Sigmoid 核函数预测精度最差,表明Sigmoid 核函数在沥青路面使用性能小样本的识别效果比较差。
2.3 ARIMA模型和SVM模型预测结果对比
选择平均绝对误差(MAE)、均方根误差(RMSE)和平均绝对百分误差(MAPE)作为对比ARIMA模型和SVM模型预测精度指标。根据表6、7的PCI值预测结果,计算出预测误差指标值见表9,图1为ARIMA模型PCI预测结果与线性核函数、多项式核函数的SVM预测结果对比。

表9 ARIMA和SVM模型预测结果评价
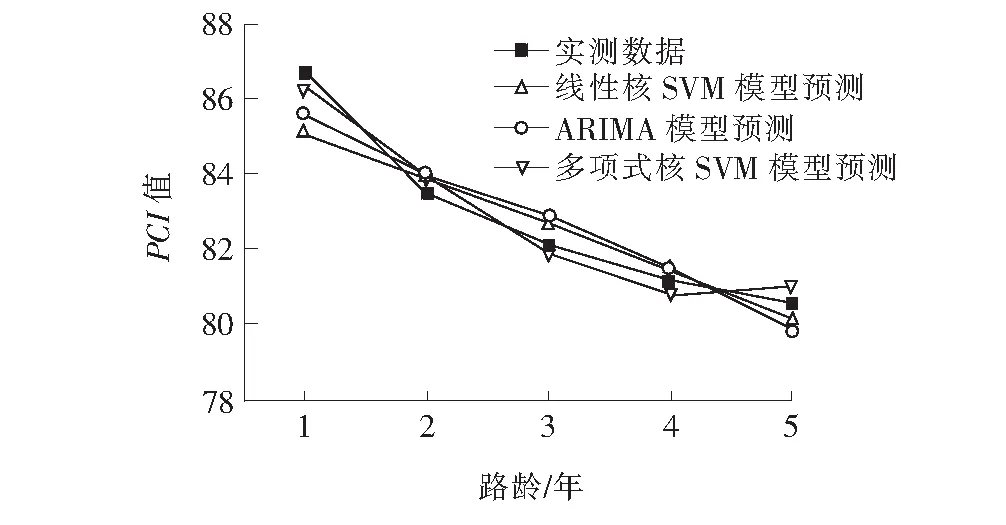
图1 ARIMA和线性核函数、多项式核函数SVM模型PCI预测结果对比
从表9和图1可以看出:ARIMA模型与线性核函数SVM模型预测的PCI变化趋势几乎一致,预测精度非常接近。ARIMA模型本质上是基于线性的模型[13],路面使用性能PCI值的时间序列数据往往包含非线性关系,因此ARIMA模型与线性核函数SVM模型预测的PCI值预测精度相对不高;多项式核函数、径向基核函数预测的PCI值比ARIMA模型预测结果精度高,多项式核函数预测的PCI值变化趋势更接近于实测值变化趋势,故可采用多项式核函数SVM模型进行路面使用性能预测。
2.4 SVM算法在沥青路面使用性能预测中的应用
针对广东省多条不同自然气候条件、交通量、结构层厚度及材料的普通国省道干线,从中统计出具有代表性的典型沥青路面结构路段在2011—2015年间的130组PCI、RQI、RDI、SRI等路面使用性能评价分项指标检测数据,利用多项式核函数SVM模型分别预测对应的PCI、RQI、RDI、SRI值。
表10为各评价指标值预测结果评价表。
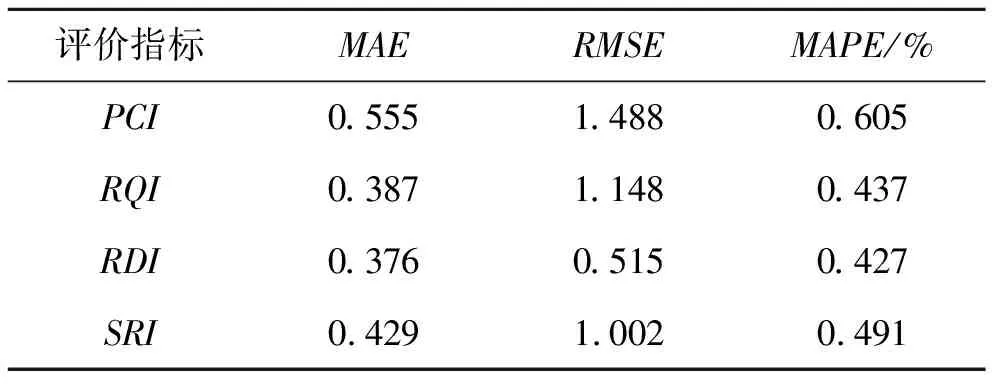
表10 ARIMA和SVM模型预测结果评价
从表10可见:PCI、RQI、RDI、SRI值预测结果平均绝对误差(MAE)、均方根误差(RMSE)和平均绝对百分误差(MAPE)最大值分别为0.555、1.488和0.605%,满足预测精度要求,体现了多项式核函数SVM模型在处理小样本非线性预测中的优越性。
3 结论
分别对比分析了基于时间序列ARIMA和支持向量机(SVM)模型的沥青路面使用性能预测结果,得出以下结论:
(1) 沥青路面使用性能数据是定期检测所获取的时间序列,采用时间序列ARIMA模型预测PCI值的精度比较高,相对误差率在1.23%以下。采用线性核函数的SVM算法预测结果与ARIMA模型预测结果很接近。
(2) 沥青路面使用性能数据少、影响路面性能衰减趋势的因素具有不确定和非线性[14],在有限数据量情况下,采用多项式核、径向基核函数SVM算法的PCI值预测结果较ARIMA模型预测结果精度高,体现出SVM模型在处理小样本非线性问题方面具有特有的优势。
(3) SVM算法中核函数对预测结果影响显著。4种核函数SVM预测模型中,基于多项式核函数模型预测精度最高,其次为径向基核函数,而Sigmoid核函数预测精度最低。采用多项式核函数SVM算法预测广东省普通国省道沥青路面使用性能的平均绝对百分误差在1%以下,满足工程实际需求。
(4) 影响沥青路面使用性能的因素非常复杂,应结合其他算法,建立考虑多因素、长周期的SVM预测综合模型,为准确预测沥青路面使用性能、制定科学的沥青路面养护决策提供参考。
