大型邮轮结构崩溃试验模型设计研究

2022-05-13裴志勇谢嗣同刘维勤吴卫国

武汉理工大学学报（交通科学与工程版） 2022年2期

裴志勇谢嗣同杨斌敖雷刘维勤吴卫国

(武汉理工大学绿色智能江海直达船舶与邮轮游艇研究中心1) 武汉 430063)(武汉理工大学船海与能源动力工程学院2) 武汉 430063)

0 引言

大型邮轮拥有多层庞大丰满的上层建筑，而且空间布置的需要，有着诸多异型或大型空间结构，这些使得上层建筑与主船体间的相互作用与普通船舶有着较大不同，进而在极端载荷下的崩溃特性也不同，对精确评价邮轮结构极限强度构成障碍.

船体结构极限强度的计算方法通常有直接计算法、Smith法、理想结构单元法、非线性有限元法和模型试验法等[1].直接计算法是假定船体梁受力状态，在现有船舶数据基础上得到的，对于新船型或新结构形式的适用性尚需系统研究.Smith法基于平断面假定，总纵弯曲作用下的船体结构极限强度计算简单易行，对弯扭联合载荷的情况需进一步验证.理想结构单元法将材料和几何非线性理想化并包含在单元中，可将较大结构单位视为一个理想结构单元，从而大幅减少自由度，降低计算时间.非线性有限元法在计算过程中为保证精度需要划分较细的网格，往往会因计算时间过长而难以实施.鉴于当前对邮轮结构功能特性及相互作用的认知不全面，系统研究尚显不足，能准确揭示邮轮结构崩溃特性和极限强度的有效方法仍是模型试验法.

根据以上分析，提出以下应对方案，即取消公共区及轨行区防护区细水雾设置。在设备区选取3个防护区采用全淹没开式系统，其他防护区采用预作用闭式系统。开式系统及闭式系统合用1套泵组，共用管网，末端在阀组箱处分开。调整后的防护区设计参数如表3所示。

模型试验法已广泛应用于传统船舶的结构极限强度研究中.Endo等[2-3]针对散货船、矿砂船分别进行了相似模型设计并进行了崩溃试验，结果表明中垂状态下的主要破坏形式是甲板和舷顶列板受压屈曲失效.杨平[4]对一条内河大重件运输船进行了相似理论分析、相似结构模型设计以及相应的崩溃试验，并将试验结果与非线性有限元计算结果进行了比较分析.

针对大型邮轮的极限强度研究，裴志勇等[5]采用理想结构单元法对断面应力线性分布和非线性分布分别进行了结构崩溃分析，结果表明：计及上层建筑和主船体相互作用的断面应力非线性分布能较好反映邮轮结构崩溃特性.陆春晖等[6]基于中国船级社《邮轮规范》(2017)整船直接计算方法，分析总纵弯曲应力和剪应力的分布规律，提出受总纵强度影响的结构设计关注点，归纳出上层建筑有效度的变化特性，并提出评估邮轮结构总纵强度的有效方法.吴剑国等[7]基于整船有限元分析，提出了一种适用于邮轮结构极限强度计算的增量迭代方法，认为主船体与上层建筑分别绕各自的中和轴弯曲，有效提高了计算精度.朱波[8]通过理论分析和数值仿真相结合的方式对上层建筑有效度及其影响因素进行了研究，可为邮轮结构优化设计和安全性评估提供参考依据.

一直以来，用结构模型崩溃试验结果预报实船极限强度是一大难题，传统的相似理论可使模型与实船结构在屈曲特性上基本一致，在屈服等非线性特性上往往差异较大.文中将理论分析与数值计算相结合，以一大型邮轮为研究对象，结合畸变相似理论和非线性相似方法来进行崩溃试验模型设计.分别进行了试验模型和邮轮实际结构的非线性有限元计算分析，并用试验模型极限强度结果预报实船，与实船计算结果进行对比分析.

1 大型邮轮结构特征

大型邮轮为满足功能性和舒适性需求，往往设计有多层丰满上层建筑，结构设计新颖且复杂多样，

（3）桁架平台正式提升前，要在一个层高的范围内上下进行提升实验，提升实验完成后，必须检查桁架主梁与电动平台三角梁连接处有无变形情况，检查主梁次梁有无变形情况，检查电动平台三角梁与立柱导向是否正常，检查电机是否过热（判断是否超负荷运转）。如果以上检查均正常视为提升实验合格。

重量重心控制使得上层建筑多采用薄板加筋结构.相较于传统船舶，文中研究的大型邮轮结构具有如下典型特征.

1) 多层丰满上层建筑邮轮主甲板以上有多层上层建筑，长度方向贯穿全船，宽度方向与船宽近似相同.

加筋板是邮轮结构的基本单位，加筋板的崩溃特性决定着船体梁的崩溃行为和极限强度[10].通常情况下，采用线性相似准则指导试验模型设计，这样模型试验可有效模拟线性屈曲行为，对于屈服等非线性行为就无从考证了.

扬中市是全国首批“国家级生态示范区”，也是苏南现代化建设示范区的重要建设城市，推进智慧城市建设是扬中经济社会发展的内在选择。

3) 舷侧开口观景需要在上层建筑舷侧设有长、大开口，影响载荷的传递，进而影响上层建筑参与总强度有效性.

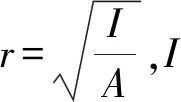
2 相似理论

2.1 相似理论基础

相似理论[9]广泛应用于探究物理现象中个性和共性、内部矛盾和外部条件之间的联系，其基础是相似三定理.

1) 相似第一定理(正定理) 对于相似的现象其相似指标皆为1，即相似准则的数值相等.

2) 相似第二定理(π定理) 若某系统有n个物理量，其中相互独立的物理量共有k个，则可用相似准则π1、π2、π3、…、πn-k之间的函数关系表示这n个物理量.

f1(π1, π2, π3,…,πn-k)=0

(1)

通常将上式称为准则关系式(π关系式)，式中的相似准则称为π项.

3)相似第三定理(逆定理) 在同一类物理现象中，如果单值量相似，并且组成这些单值量的相似准则相等，则可认为此类现象相似.

2.2 线性相似准则

随着薄壁结构在工程中的广泛应用，传统的相似理论进一步发展，将薄壁结构的厚度参数独立于其他线尺度参数成为一个独立的基本量纲，形成了畸变相似理论.

综上所述，术前伴有膝前痛及髌股关节退变并不影响Oxford内侧单髁置换术短中期疗效。作者认为髌股关节退变不应作为UKA的绝对禁忌证，但应做好单髁置换转全膝关节置换的准备，如术中发现有大面积的严重髌股关节软骨全层破坏并不适合行单髁置换术，可转为全膝关节置换术治疗。但本研究的病例数量较少，随访时间短，今后尚需要进行大宗病例的长期随访研究。

邮轮是典型的薄壁结构，可使用畸变相似理论进行模型设计，根据弹性力学相关知识，船体梁弯曲相似准则为

(2)

采用ABAQUS软件，应用动态显示算法，计算得到试验模型的逐次崩溃行为.首先在中拱弯曲载荷作用下船底板格发生屈曲，随着载荷的进一步增加，船底板架、内底板架相继屈曲，结构达到极限状态，随后结构丧失承载能力，曲率增加的同时弯矩进一步降低.逐次崩溃过程见图4，弯矩-曲率关系见图5.

文中研究基于畸变相似理论和非线性相似方法进行试验模型设计，在满足试验要求前提下尽可能简化加工工艺，考虑试验场地与加载能力等客观条件.综合考虑各因素，确定邮轮实际结构与模型的几何相似比为CL=8∶1.

(3)

2.3 弯曲非线性相似方法

合约规划是目标成本实现的第一步。在建设工程项目确定目标成本后，就需要按照分解的目标成本进行合约规划。合约规划不能简单地理解为只服务于成本管理，其还应服务于整个项目管理，即服务于招标、采购、施工、销售及运维等。合约的规划要综合考虑以下因素。

雌飞鱼会小心翼翼地将鱼卵产在棕榈叶的叶柄上，它们的卵又轻又小，卵的表面有许多丝状突起物，这些呈丝状且有一定黏性的突起物可以把飞鱼卵牢牢地缠在棕榈叶上。

通过加筋板在压缩载荷作用下的崩溃特性研究表明，加筋板的非线性行为与板细长比β和加强筋柔度系数λ密切相关.板细长比β可用来表征板格的崩溃特性，柔度系数λ可用来表征加强筋的崩溃特性，即

（5）星日天步星君，司服舉，立秋日紏葛紏治。（《太上說玄天大聖真武本傳神呪妙經註》卷一，《中华道藏》30/533）

(4)

4) 上层建筑与主船体连接救生艇布置的需要使得主船体与上层建筑的舷侧壁不是直接相连，是通过支柱连接.

将上述弯曲非线性相似方法用以指导模型设计，使得试验模型的β和λ与邮轮结构相同，因此它们在弯曲载荷作用下的崩溃特性也会相同，这样就可以用模型崩溃试验得到的极限强度预报实际邮轮结构的极限承载能力.

3 试验模型设计

3.1 线性相似比确定

但需要注意的是，等离子手术对病例筛选严格，术前需通过相关检查全力分期病变，对侵犯较广的和分化较低的病理类型仍应选择开喉手术，以降低复发率；且低温等离子微创手术热效率低，其止血效果有限，遇到动脉性出血时必须谨慎处理。

邮轮结构是典型的薄壁结构，若厚度相似比取与几何相似比相同，会导致板厚非常小而实际上无法实施.基于畸变相似理论，将厚度视为一个独立的参数，综合考虑试验成本、试验室条件、加工条件和工艺等问题，确定厚度相似比为Ct=3∶1.邮轮与试验模型主尺度表见表1.

表1 邮轮与试验模型主尺度单位：mm

3.2 弯曲相似模型设计

为了使模型崩溃试验结果能预测实际邮轮结构的极限强度，试验模型在设计时既要考虑屈曲等线性相似行为，还要考虑屈服等非线性相似行为，使得典型加筋板结构除了线尺度相似，同时板格细长比和加强筋柔度系数也基本相同，这样试验模型的屈曲、屈服行为以及崩溃特性就会与实际结构保持一致.试验模型结构设计流程见图1.

图1 崩溃试验模型设计流程

为使试验模型能较好模拟邮轮结构崩溃特性，二者的板细长比β和加强筋柔度系数λ应相同.典型试验模型和邮轮结构的板格及加强筋尺寸，细长比和柔度系数比较见表2，中和轴位置、剖面积和剖面惯性矩等剖面特性比较见表3，二者较好吻合表示试验模型能反映实际邮轮结构的基本特性.

表2 典型加筋板结构参数

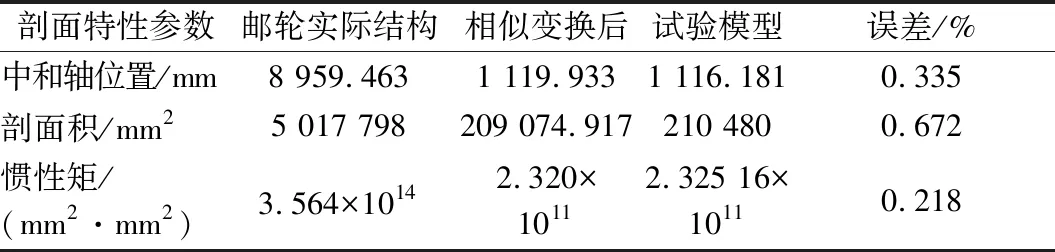
表3 剖面特性比较

3.3 试验模型结构设计

试验模型包含三个舱段，中间舱段为试验段，向船艏、船艉各延伸一个舱段，在首尾舱段施加载荷和边界条件.为探究上层建筑层数等对邮轮结构崩溃行为的影响，试验模型共设有八层上层建筑，主甲板记为D0甲板，依次往上分别记为D1甲板、D2甲板直至D8甲板.

4 试验模型有限元分析

4.1 计算模型

极限强度计算分析是一个非线性过程，需要划分精细网格才能达到要求的精度.参照Paik对计算模型范围的研究成果[11]，为节省计算时间，本节中采用双跨(double-span section)结构模型进行极限强度计算.取半宽模型，以强横框架为中心向首向尾各半个强横框架间距，纵骨采用板单元模拟，纵骨间划分8个单元，纵向划分12个单元，共有135 385个单元，见图2.

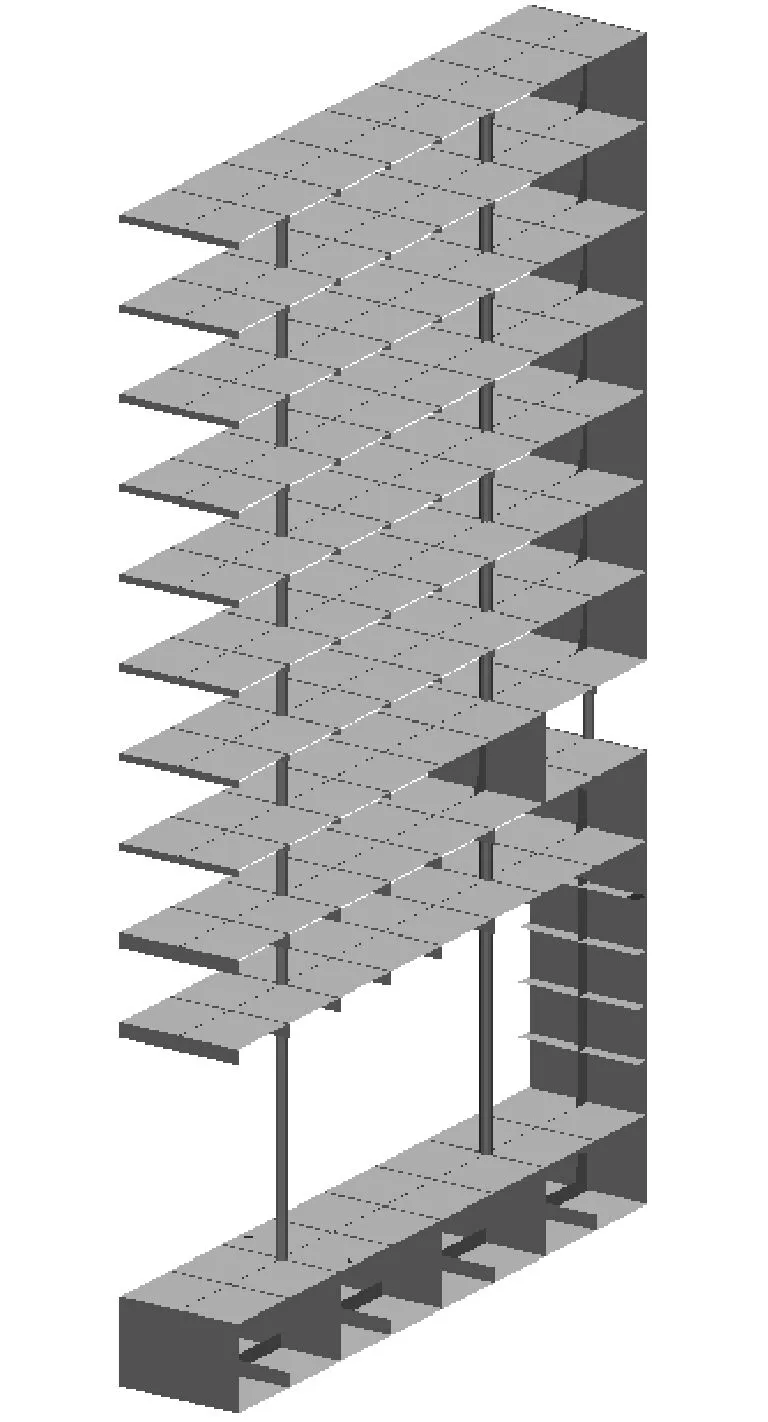
图2 双跨计算模型

模型的首尾端面假设为平断面，在首尾端面施加强制转角，计算得到端面弯矩和相应的曲率，逐渐增大直至结构发生崩溃为止，得到弯矩-曲率关系曲线，最大弯矩即为结构的极限强度.边界条件示意图见图3.

一是强化果农技术培训。推广水果生态栽培新技术，扩大示范，认真组织实施科技培训计划，完善培训手段，注重果农实用技术素质的提高，每年培训果农100人次，尽快使全县果树种植户都有1名技术明白人；二是进一步优化果树品种结构。以市场为导向，立足当前，着眼长远，加快新优品种的引进、繁育、示范、推广，从品种上抢占果业发展的制高点。

图3 加载及边界条件示意图

4.2 计算结果及分析

试验模型与实船满足的弯曲设计准则为惯性矩相似，即

2) 支柱结构辉煌空间布置需要大跨度空间结构，广泛使用布置在纵桁和横梁相交处的支柱做支撑.

图4 中拱状态下试验模型逐次崩溃模态

图5 双跨模型弯矩-曲率关系曲线图

由图5可知:在中拱弯曲载荷作用下，试验模型中拱极限弯矩为4.351×107N·m，在中拱弯矩达到2.285×107N·m时，最上层甲板(D 8甲板)首先达到屈服应力，随后D 7甲板、D 6甲板、D 5甲板和D 4甲板相继达到屈服应力，同时船底板发生板格屈曲；随着中拱弯矩增加达到3.923×107N·m时，船底板板架发生总体屈曲；随着载荷的进一步增加至4.351×107N·m时，船底板、内底板及舷侧板架发生总体屈曲，结构达到极限状态，丧失承载能力；随后，中拱弯矩减小，曲率持续变大，最后塑性变形集中在D 8甲板、D 7甲板和船底板靠近端面局部区域.

5 邮轮实船有限元计算

5.1 实船计算及分析

与试验模型计算一致，建立双跨结构模型，为有效减少计算工作量，采用半宽模型，纵骨间划分8个单元，纵向划分8个单元，共有112 222个单元.采用非线性有限元软件ABAQUS，计算得到邮轮实船结构的逐次崩溃行为见图6，弯矩-曲率关系曲线见图7.

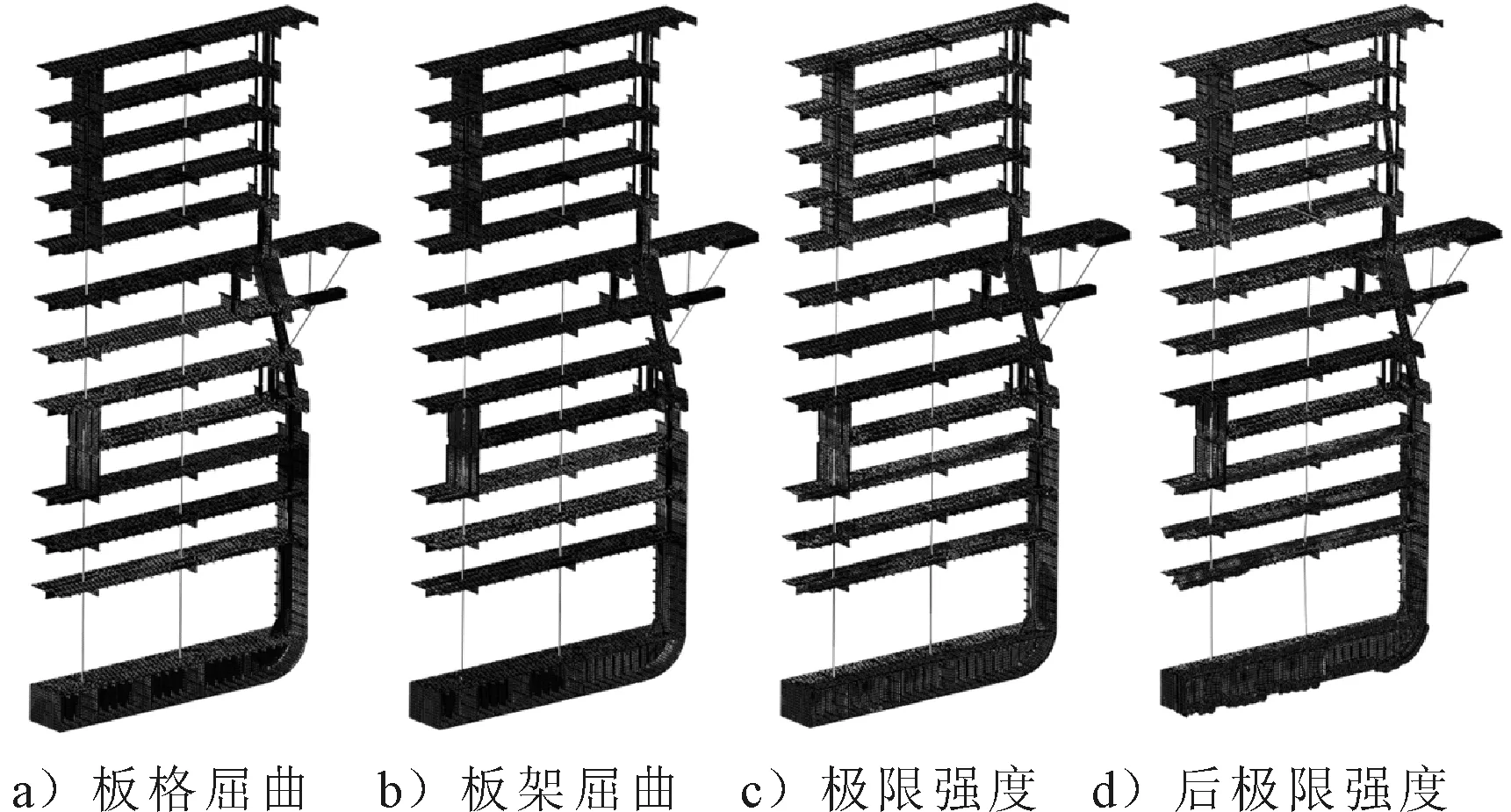
图6 中拱状态下邮轮实船结构逐次崩溃模态

图7 邮轮弯矩-曲率曲线图

根据数值计算结果可知，当中拱弯矩达到5.173×109N·m，最上层甲板首先达到屈服应力，随着弯矩逐渐增大，上层建筑最上四层甲板依次达到屈服应力，同时船底板发生板格屈曲.中拱弯矩达到7.719×109N·m时，船底板、内底板和主船体舷侧板发生总体板架屈曲.载荷进一步增大，中拱弯矩为8.721×109N·m的，结构达到极限强度，丧失承载能力；随后，中拱弯矩减小，曲率持续变大，最后塑性变形集中在上层建筑上四层甲板和船底板、内底板及舷侧板靠近端面处.

模糊控制器的输入分别为滤波后船舶的功率需求Pr、电池模块的荷电状态SOCb、超级电容模块的荷电状态SOCc，输出为超级电容模块的功率分配因子Kc。定义Kc为超级电容模块所提供的功率占功率需求的比例。

5.2 实船极限强度预报

(5)

式中：Mm为试验模型极限强度；Ms为邮轮实船极限强度.

分别对模型和实船进行了非线性有限元计算分析，将模型计算结果按相似方法预报至实船，并与实船计算结果比较见表4，二者的直接误差为4.208%.传统基于线性相似分析设计的模型可对实船屈曲等线性行为较好模拟，预报实船极限强度往往有着较大的差异.文中采用畸变相似理论和非线性相似方法相结合进行试验模型设计，在屈曲和屈服阶段都能较好地模拟实船结构的行为，因此可根据模型崩溃试验结果预报实船的极限强度.

推荐理由:《水土保持设计手册》是我国首次出版的水土保持设计方面的工具书，获得了国家出版基金的资助并被列为“十三五”国家重点图书出版规划项目。手册概括了我国水土保持规划设计的发展水平及发展趋势，是一部合理收集新中国成立以来水土保持规划设计经验，符合新时期水土保持工作需要的综合性手册。手册共分三卷，包括专业基础卷、规划与综合治理卷和生产建设项目卷，内容丰富、资料翔实，编入了大量数据、图表和新资料、标准，并附上了典型案例，具有科学性、实用性、综合性、协调性的突出特点。