高能级强夯地基振动传播规律研究
2022-05-12李晓雷唐龙龙
李晓雷,唐龙龙
(1.沧州市黄骅港务局,河北沧州 061100;2.中交第一航务工程勘察设计院有限公司,天津 300220)
引言
强夯法是加固地基的常用方法之一,具有加固效果显著、适用性广、施工便捷和费用低等优点[1]。强夯时产生的剧烈振动,对周围环境及建(构)筑物有着不可忽视的影响[2]。实践表明强夯时的地面振动会产生衰减。如果能得到强夯地面振动随距离衰减的一般规律,并对强夯施工振动最小安全距离进行量化,将为今后的强夯设计、施工以及安全评价提供依据,具有重要的理论和实践意义[3-5]。国内外大量学者为此进了不懈努力,并取得了很多成果。笔者结合某强夯试验将这些成果中的各个方法优劣进行了比较分析,在此基础上提出了新的衰减公式,最后探讨了强夯振动衰减的影响因素。
1 工程概况
拟建工程主要包括52 座储油罐、4 座消防水罐区及配套的管线管廊、道路、消防站、事故处理设施及相应的建(构)筑物。拟建场地地貌单元原属于海岸带地貌,为原有海域或养殖池经人工回填整平而成。
为判断置换强夯法在本场地进行地基处理的适宜性;确定处理后的有效加固深度范围内的地基承载力和变形指标;确定夯点间距、夯击遍数、最后两击沉降量平均值和间隔时间等相关参数;确定强夯施工振动、侧向挤压等对周边环境和工程的影响;确定与周边工程的最小安全距离;确定二期工程内的强夯范围进行强夯试验。
2 振动测量方案
本次试验测定两种锤形三种夯击能共计4 个工况的振动参数。
工况2:锤型为平锤,落锤质量40 t,落距15 m,夯击能为6 000 kN·m,锤径2.8 m;
工况3:锤型为柱锤,落锤质量30 t,落距34 m,夯击能为10 000 kN·m,锤直径1.5 m;
工况4:锤型为平锤,落锤质量40 t,落距30 m,夯击能为12 000 kN·m,,锤直径2.8 m。
各工况分别夯击8 次,强夯区距最近建筑物为80 m,以上4 种工况分别距离夯点10 m、20 m、30 m、40 m、50 m、60 m、70 m、80 m 处布置径向、切向及垂向布置测点,共计24 个测点。[6]
3 振动测量结果及分析
3.1 测试结果
强夯施工引起的地面振源的振动强度可用夯击能量来衡量,本次测试夯击能量分别为 6 000 kN·m、10 000 kN·m、12 000 kN·m。距离夯点每10 m 进行震动测试,分别记录不同工况下各个测点的振动速度峰值和主频,统计结果见表1。

表1 各工况各测点振动测试统计结果(夯击1 次数据)
从结果可以看出随着夯击能增大峰值振动速度变化不显著,相反,锤型的改变对于峰值振动速度变化影响较明显;柱锤的径向振动峰值振动速度最大,竖向次之,切向最小;平锤的径向峰值振动速度与竖向振动峰值速度较大,切向较小;表明地表振动以径向向前传播为主。
3.2 指数函数拟合
在众多对振动衰减公式的研究中,尤以幂函数最广,其通用函数如下:
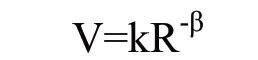
式中:
冯飞常务副省长赴省国土资源厅调研(省厅新闻宣传中心 ) ...........................................................................2-4
k 为当量系数;
β 为振动衰减系数;
R 为测点距夯点距离;
V 为振动峰值速度。
试验拟合结果见表2。

表2 各个工况下拟合结果
从拟合结果可以看出,利用幂函数拟合得到的结果中参数β 相对稳定,均在1.32 至2.71 之间,而参数k 离散型较大。各个工况各个方向的拟合结果较好,相关系数大于等于0.9684。
3.3 指数函数拟合
有关研究表明强夯地表振动衰减更符合指数函数的规律,其通用函数如下:

式中:
k 为振动系数,α 为振动衰减系数;
R 为测点距夯点距离;
V 为振动峰值速度。
试验拟合结果见表3。

表3 各个工况下拟合结果
由拟合结果可以看出,利用指数函数拟合得到的结果中参数α 均在0.07 至0.26 之间,有一定的离散型,参数k 离散型较大,这与锤型、振动方向及夯击能有关。而各个工况各个方向的拟合结果与幂函数拟合比较稍差,相关系数大于等于0.8605。
3.4 幂指数函数拟合
然而无论是幂函数还是指数函数,用于描述振动的衰减规律都是不够准确的。因此本文将幂函数与指数函数相结合,得到幂指数函数,其通式如下:

式中:
k、α、β 均为振动衰减系数;
R 为测点距夯点距离;
V 为振动峰值速度。
本次试验拟合结果见表4。
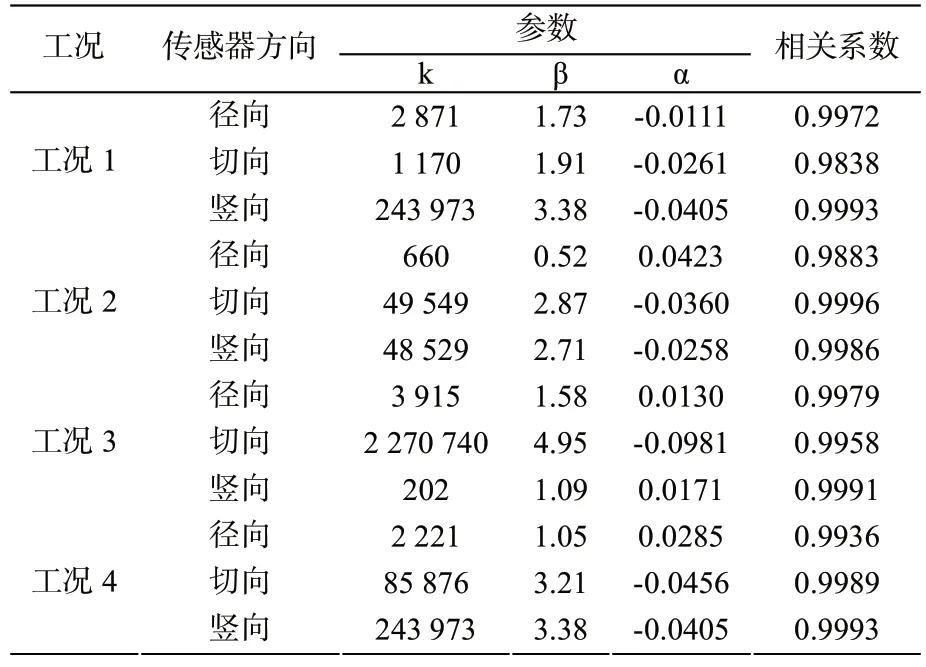
表4 各个工况下拟合结果
由拟合结果可以看出利用指数函数拟合得到的结果中参数α、β 均有一定离散型,参数k 离散型较大,但与其他拟合结果相比拟合效果最好,其相关系数大于等于0.9838。
4 结语
本次试验可以得到以下几点结论,从拟合结果整体来说幂指数函数拟合最好,幂函数拟合其次,指数函数拟合最次,这说明强夯振动在地表衰减过程中是以幂指数函数的形式衰减,其中幂函数衰减为主要衰减形式,指数衰减为次要衰减形式;衰减函数中参数α 作为幂函数衰减的过程中的影响因子,主要与振动的传播介质有关,夯击能、振动方向以及锤型影响稍小,其影响程度中振动方向最强,锤型次之,夯击能影响最弱;参数β 作为指数衰减过程中的影响因子,其主要与传播介质有关,与夯击能、振动方向以及锤型无关;参数k 作为衰减规律的综合影响因子,与各个方面因素均有关,但主要影响因素为传播介质及振动的方向。
