赋权类非线性学术评价方法伪权重及权重失灵研究——以TOPSIS评价方法为例

俞立平 何庆光 韩 钰

(1.浙江工商大学 统计与数学学院 杭州 310018；2. 广西财经学院 信息与统计学院 南宁 530007；3.沧州师范学院 经济管理学院 沧州 061001)

0 引 言

在学术评价中多属性评价方法得到广泛应用。多属性评价方法采用指标体系进行评价，可以从多个视角如影响力、创新性、贡献、绩效等角度对学科、团队、大学、期刊等进行评价，从而全面反映学术评价对象现状与发展水平[1-4]。目前较有影响力的学术评价均采用多属性评价方法，如教育部学科评价、北大核心期刊评价、各类大学排名等。

学术评价工作越来越得到各界的关注。目前研究的焦点包括破“五唯”背景下的学术评价，基于创新能力/质量/实效/贡献的学术评价、代表作评价等等，更多集中在评价导向、评价对象与评价内容上，但是对学术评价方法却极少关注，如果学术评价方法中的一些基本问题不加以解决，同样对学术评价成果会产生较大的影响，并且这种影响是隐藏的，必须加以重视。

多属性评价方法大致可以分为线性评价方法与非线性评价方法两类(见图1)。所有的线性评价方法均涉及权重，而非线性评价方法中，仅有一部分评价方法涉及权重，如TOPSIS、VIKOR、灰色关联等，称为赋权类非线性评价方法；还有一些非线性评价方法不涉及权重，如主成分分析、因子分析等，称为非赋权类非线性评价方法，当然还有一种分析视角是将其视为等权重。至于权重确定方法，包括主观权重、客观权重、主客观权重三大类。主观赋权方法包括层次分析、专家会议法、德尔菲法等，客观赋权方法包括熵权法、变异系数法、概率权法等，主客观赋权法则是前两者方法的综合。目前多属性评价方法已经有几十种，以非线性评价方法为主。

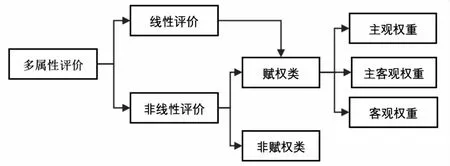
图1 多属性评价与权重关系

鉴于多属性评价方法分类比较复杂，本文重点研究赋权类非线性评价方法的伪权重与权重失灵问题，其他相关问题另外进行研究。TOPSIS评价方法是一种典型的赋权类非线性多属性评价方法，因此本文以TOPSIS为例开展相关研究，其研究范式可推广到其他赋权类非线性多属性评价方法。

TOPSIS是一种影响力较广的评价方法。TOPSIS又称为理想解法，最早由Huang[5]提出，它在考虑专家权重的基础上，兼顾评价对象到理想解与负理想解的相对距离来进行评价，是非线性评价方法的重要代表。2021年2月17日，在中国知网查询篇名、关键词、摘要中包含“TOPSIS”的核心期刊论文就有4 458篇，全部期刊论文高达15 927篇，可见TOPSIS评价方法应用的广泛性与影响力。

TOPSIS在学术评价中也得到了广泛的应用，目前已经有数百篇学术评价论文涉及TOPSIS评价。王萝娜、李端明[6]采用加权TOPSIS评价了学术图书的影响力。奉国和、周榕鑫等[7]采用熵权法和因子分析计算权重，然后通过加权TOPSIS对学术期刊进行评价。张发明、庾凡等[8]在学术期刊评价中分别采用GRA和TOPSIS法进行评价，然后采用组合评价法得到最终评价结果。熊国经、熊玲玲等[9]首先采用因子分析法提取公共因子，然后采用熵权法修正公共因子的权重，最后采用TOPSIS法对学术期刊评价。俞立平、潘云涛等[10]则比较了TOPSIS中距离函数幂次对学术期刊评价的影响。王颖、蓝云飞等[11]运用TOPSIS分析法对中部6省科技服务业发展水平进行评价。杨秀玉[12]运用熵权TOPSIS对我国30个省市农业科技创新能力进行评价。

在以TOPSIS为典型代表的非线性学术评价中，伪权重问题是其中一个重要的系统误差。所谓伪权重，就是指TOPSIS评价中评价赋权与实际权重并不一致，这里评价赋权包括主观赋权、客观赋权和主客观赋权。实际权重概念由俞立平、潘云涛等[13]提出，其基本原理是将非线性评价方法的评价值与评价指标进行回归，然后将各指标的回归系数进行归一化处理，就得到各指标在评价中的重要性大小即实际权重，很明显评价赋权与实际权重并不一致，这就是伪权重问题，该问题是非线性评价中的隐含问题，无疑对评价会产生较大的影响。

权重失灵是非线性评价中另一重要系统误差，在TOPSIS中当然也同样存在。所谓权重失灵，就是指当不同评价指标数据出现“同增同减”现象时，此时无论评价赋权组合如何变化，评价值的排序基本不变，相当于权重在评价中没有发挥作用。权重失灵现象同样是个隐含问题，对非线性评价的影响尚处于探索之中。

伪权重与权重失灵问题的研究尚处于起步阶段。其形成的原因，产生的影响，以及两者关系有待进一步研究。

研究伪权重与权重失灵对TOPSIS评价的影响机制具有重要意义。两者均与权重相关，而权重在整个学术评价中具有非常重要的地位。两者均属于隐含问题，而且其影响是系统性的，其产生与影响机制有待进一步探索。对于两者之间的关系也有待探讨，比如说伪权重的存在会增加误差，但权重失灵一定程度上似乎会减小误差，这是个十分有趣的问题。相关问题的研究不仅对于情报学与科学学方法论具有重要意义，也推进了多元统计理论的研究，在实践中，对于保障学术评价方法的科学性，加强学术评价质量，提高学术评价的公平与公正。

1 理论分析与研究方法

1.1TOPSIS评价方法的原理TOPSIS计算公式为

Cij=

(1)

公式(1)中，Cij表示TOPSIS的评价值，Xij为标准化后的评价指标，ωj表示评价指标权重，Xj+为标准化后的指标极大值(称为理想解)，Xj-为标准化后的指标极小值(称为负理想解)，i、j分别为评价对象和评价指标序号；n为评价指标数量。分子表示评价对象到负理想解的距离，分母为评价对象到正负理想解的距离之和。

TOPSIS是赋权类非线性评价方法的一个代表，尽管各种赋权类非线性评价方法原理不同，但总体上存在以下共同特征：

第一，评价指标与评价结果之间存在非线性关系，这种非线性关系的在不同评价方法中表现不同。

第二，评价中会用到权重，但权重与评价结果之间的关系一般也是非线性的。

第三，很难评价权重在评价中的作用，因为不同非线性评价方法对权重的利用原理不同。

1.2TOPSIS评价方法的线性转换线性评价是传统学术评价中应用最多的方法之一，通常情况下，线性学术评价的计算公式如下：

Cij=ω1Xi1+ω2Xi2+...+ωnXin

(2)

线性评价原理简单，权重作用清晰，分析容易，克服了非线性评价深度分析的一些困难。如果能将非线性评价方法转化为线性评价方法，这将非常有利于后续的进一步分析。俞立平、潘云涛等[9]提出可以将非线性评价值作为因变量，评价指标作为自变量进行回归，回归系数大小就反映了各评价指标对评价值的相对重要性，将其进行归一化处理就是非线性评价指标的模拟权重，也称为实际权重。

通过实际权重的计算，不仅将复杂的非线性评价方法转化为相对简单的线性评价方法，有利于后续深度分析，而且也暴露了非线性评价的伪权重问题。

1.3TOPSIS的伪权重问题及其产生机制伪权重问题是指评价赋权与实际权重不一致的现象。在TOPSIS评价中，其实有两种权重，第一种权重是评价赋权，一般采用专家赋权法，当然也可以采用其他方法赋权。另一种权重是隐含的，即将TOPSIS转化为线性评价时的实际权重，很明显这两种权重不一致，这对评价赋权是一种扭曲，真正重要的指标可能变得不重要，而不重要的指标变得重要。所以伪权重是TOPSIS方法存在的一个重要问题，必须引起足够的重视。

赋权类非线性评价方法伪权重问题产生的原因主要包括以下几个方面：

第一，评价方法算法。不同非线性评价方法的算法和原理各不相同，对评价赋权的利用大小也各不相同，其特征一般难以掌握。

第二，评价指标数据分布。在学术评价中，评价指标数据分布往往相差较大，有的服从正态分布，有的服从幂律分布，有的服从其他分布，而这一切对实际权重计算会产生较大影响。

第三，模拟权重拟合算法。对于非线性评价方法而言，实际权重是通过回归拟合计算得到的，是一种模拟权重，拟合方法可采用岭回归或偏最小二乘法等，当然拟合方法不同，对实际权重也会产生一定的影响。

综上所述，对于TOPSIS评价方法而言，伪权重问题是客观存在的，可以分析计算其大小，但要消除几乎是不可能的。

伪权重的测度可以根据实际权重与专家权重的平均偏离度来进行测度，即每个指标权重偏离程度的平均值表示。计算公式如下：

(3)

式(3)中，Wj为实际权重，ωj为专家权重，B为伪权重水平，该值越大，说明伪权重问题越严重。

1.4TOPSIS的权重失灵及产生机制前文已经将TOPSIS转换为线性评价，因此暂且将TOPSIS评价视为线性评价，来讨论其权重失灵问题。

对于k个评价指标，P和Q两个评价对象的指标值分别为P1、P2…Pk和Q1、Q2…Qk，评价指标的权重为ω1、ω2…ωk。考虑一种极端情况，当评P和Q“同增同减”时，比如对每个评价指标，均有Pi>Qi，CP和CQ分别为P和Q评价值。

(4)

下面比较P和Q评价值之差：

CP-CQ=ω1(P1-Q1)+ω2(P2-Q2)+…

+ωn(Pn-Qn)>0

(5)

也就是说，权重组合ω1、ω2…ωk无论如何变化，CP永远大于CQ，这就是权重失灵。

评价指标“同增同减”的本质就是评价指标之间高度相关，鉴于TOPSIS评价方法已经转化为线性评价方法，所以当评价指标高度相关时，TOPSIS也会出现权重失灵。

关于权重失灵的测度，可以比较不同权重组合评价结果之间的平均排序变化，假设权重组合A的评价值排序为RA，权重组合B的评价值排序为RB，m为评价对象数量，则AB之间的权重失灵度VR为

(6)

VR越小，说明权重失灵度越高。当权重组合为k个时，权重组合的两两失灵度共有Ck2个，取其平均值，就可以得到总体权重失灵度：

(7)

1.5伪权重与权重失灵的关系对于TOPSIS评价而言，通过将其转化为线性评价方法，这样就可以进一步研究伪权重与权重失灵的关系了(见图2)。

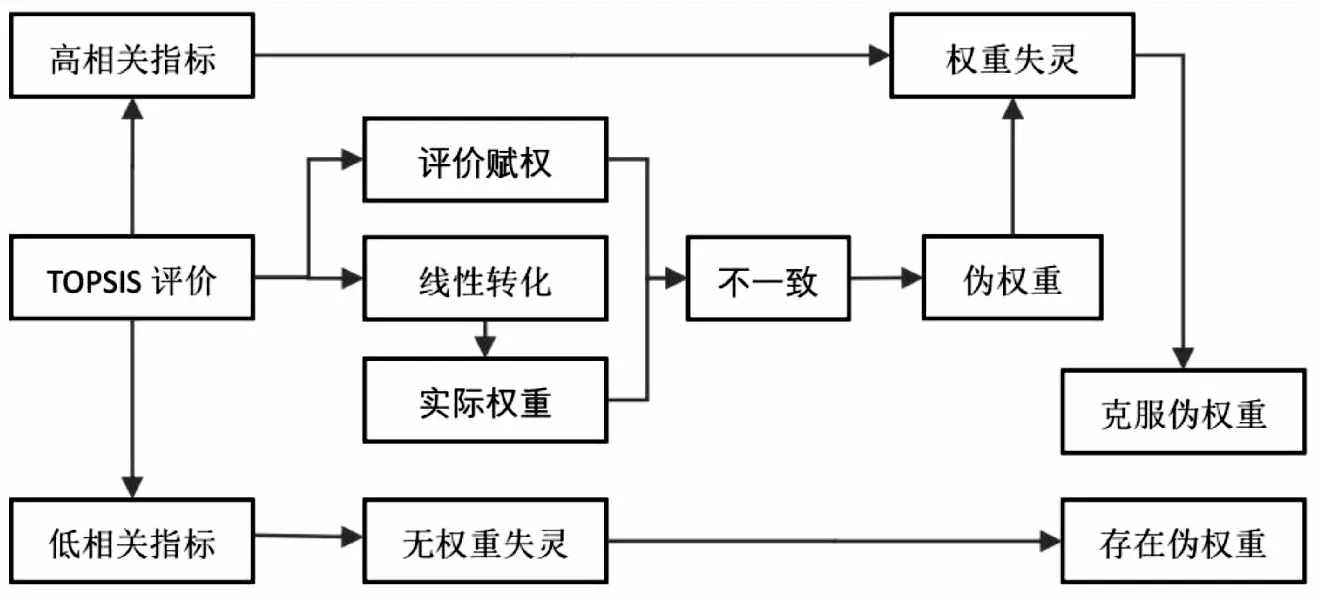
图2 TOPSIS伪权重与权重失灵的关系

TOPSIS评价存在两种权重，一种是评价赋权(专家权重)，另一种是实际权重，两者并不一致，也就是说存在伪权重问题。对于高相关指标而言，由于存在权重失灵，不管权重组合如何变化，评价结果的排序大致不变。也就是说，尽管专家权重与实际权重并不一致，但对评价结果排序影响甚微，结论就是由于权重失灵的存在，使得高相关指标TOPSIS评价的伪权重负作用大大降低，或者说，权重失灵一定程度上解决了高相关指标TOPSIS评价的伪权重问题。

对于低相关指标而言，由于并不存在权重失灵问题，因此也不能有效解决伪权重问题。

2 研究框架与研究数据

2.1研究框架本文以JCR管理学期刊为例来研究相关问题。根据上文分析，将评价指标分为三组分别计算权重失灵程度并进行比较，三组分别是高相关系数指标、低相关系数指标、全部评价指标。每组均采用专家赋权线性评价以及TOPSIS评价，并比较两者的权重失灵度，本质上TOPSIS评价相当于采用实际权重线性评价，与专家赋权线性评价相当于是两种权重组合进行评价。

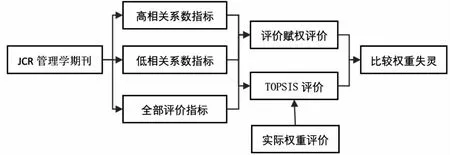
图3 研究框架

根据前文分析，可以大致估计实证结果，即高相关系数指标评价会出现权重失灵，低相关系数指标不会出现权重失灵，而全部指标评价由于相关系数介于两者之间，因此权重失灵水平处于中等水平。

2.2研究数据本文研究数据为JCR2019管理学期刊的文献计量指标，作为一个算例，以管理学期刊影响力评价为例，选取7个评价指标，分别是：影响因子IF、5年影响因子IF5、他引影响因子IFW、即年指标II、总被引频次TC、特征因子ES、论文与影响分值AIS。至于评价赋权，采用专家赋权，充分征求学术期刊评价领域的6位专家，最终权重如表1所示。

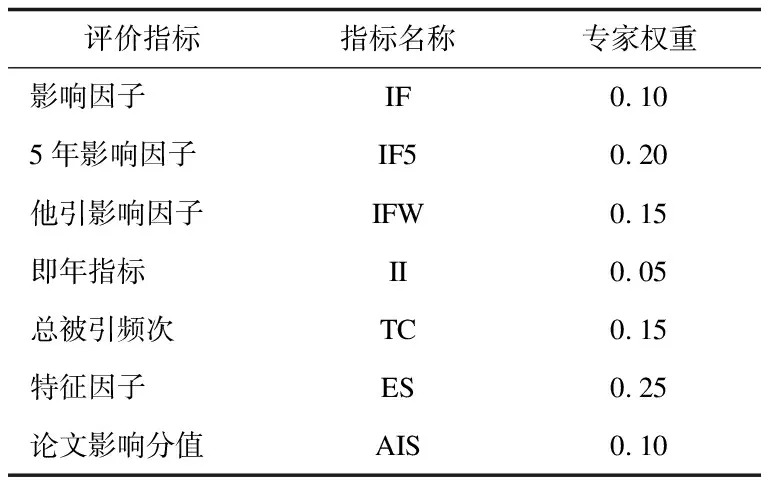
表1 评价指标及权重

管理学JCR2019共有期刊225种，部分指标存在数据缺失，必须进行必要的清洗，经整理后还有193种期刊。原始数据的描述统计如表2所示。从Jarque-Bera检验值和对应的p值看，所有评价指标均不服从正态分布。

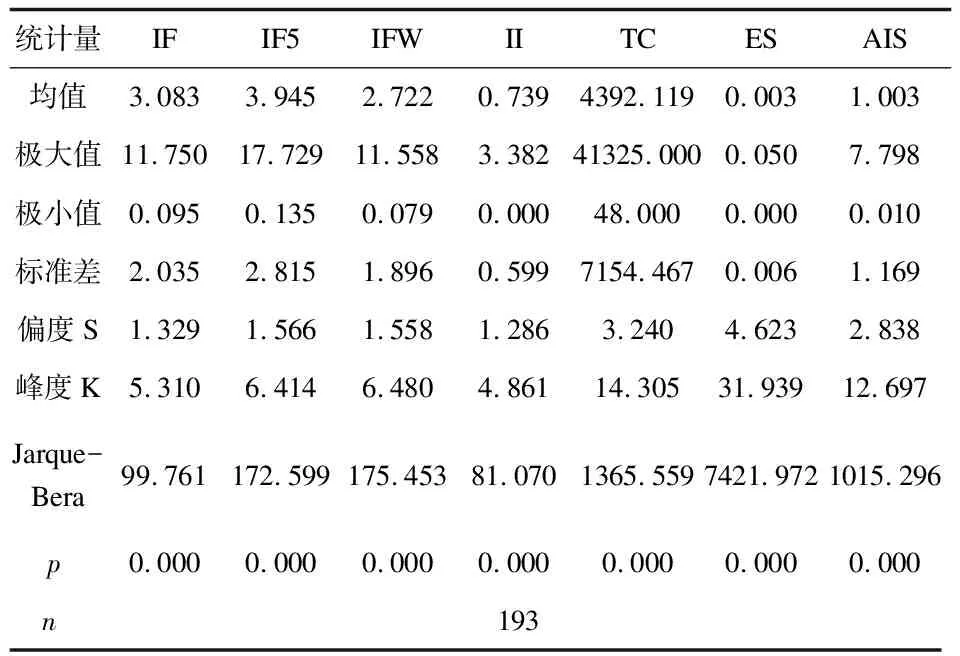
表2 评价指标描述统计

3 实证结果

3.1评价指标相关系数首先要计算评价指标相关系数，以筛选出高相关指标、低相关指标供进一步研究。相关系数如表3所示，经分析发现影响因子、5年

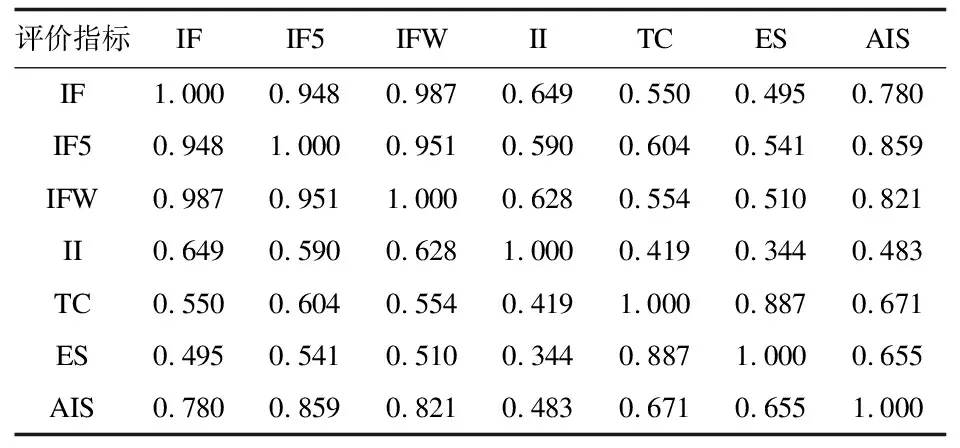
表3 相关系数表

影响因子、他引影响因子之间的相关指数较高，平均相关系数0.962，因此将这三个指标作为高相关指标用于TOPSIS评价比较。剩下的4个指标包括即年指标、总被引频次、特征因子、论文影响分值，其平均相关系数为0.577。全部7个指标的平均相关系数为0.663，介于高相关指标与低相关指标之间。

3.2高相关指标TOPSIS评价分析影响因子、5年影响因子、他引影响因子三个高相关指标评价赋权分别为0.10、0.20、0.15，将其等比例转化为标准权重，使其总和为1 ，权重分别为0.22、0.44、0.34，采用TOPSIS进行评价，同时采用专家权重进行线性评价，结果如表4所示，由于篇幅所限，本文仅公布评价赋权线性评价前30的期刊。

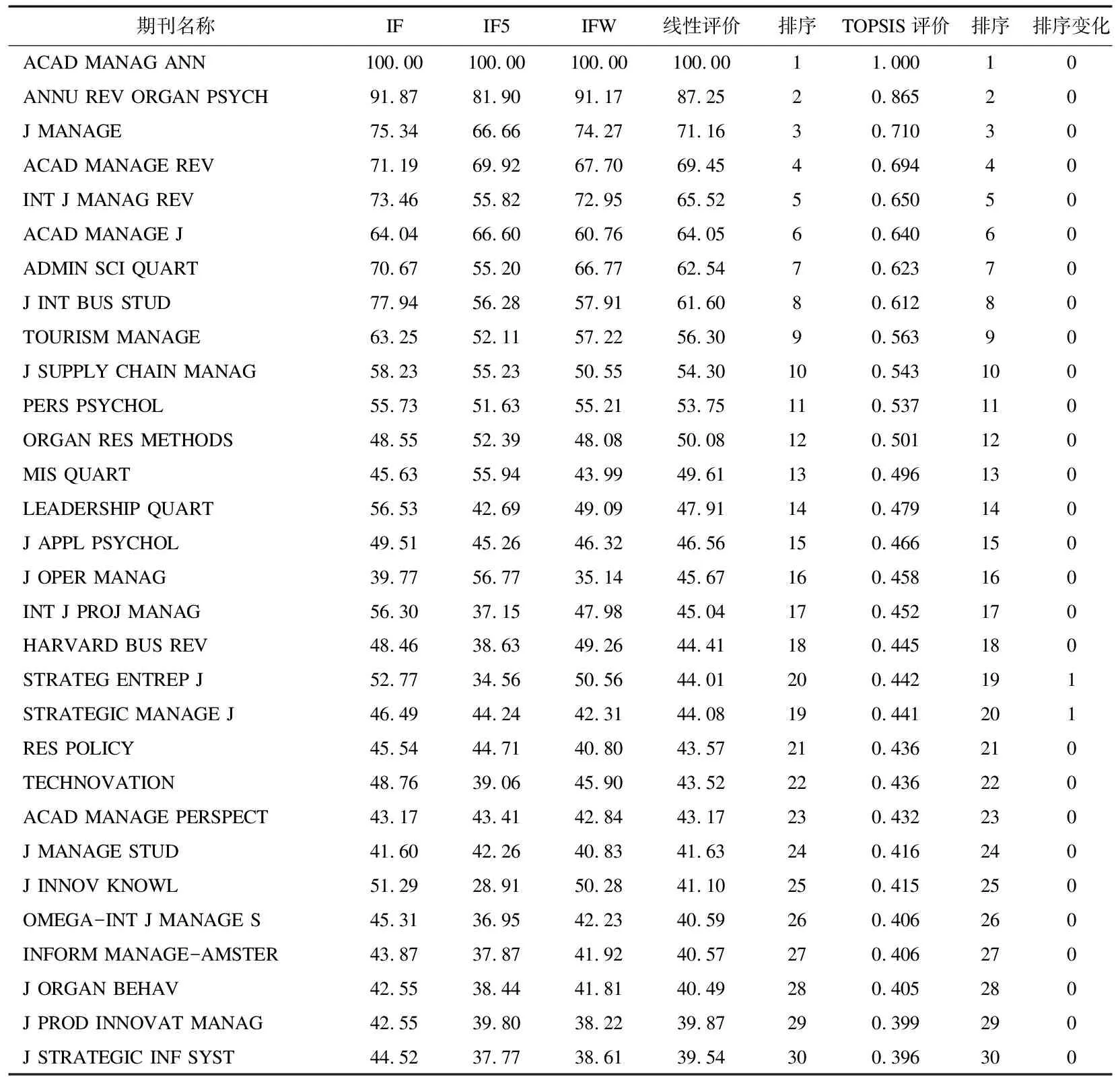
表4 高相关指标评价排序比较

下面计算实际权重，为了降低评价指标多重共线性的影响，采用岭回归对高相关指标评价值与评价指标进行回归，当标准系数之和为0.7时，模型趋于稳定，拟合优度为0.942，具有很好的拟合效果，因此取此时的回归系数作为最终结果。

进一步将回归系数进行归一化处理，得到评价指标的实际权重，如表5和图4所示。TOPSIS的实际权重最大的为5年影响因子0.440，其次是影响因子0.329，最后是他引影响因子0.327，而专家权重最大的为5年影响因子0.440，其次是他引影响因子0.340，最后是影响因子0.220，专家权重与实际权重存在较大差异。三个指标的权重差异分别为49.55%、21.82%、3.82%，平均差异为25.06%。

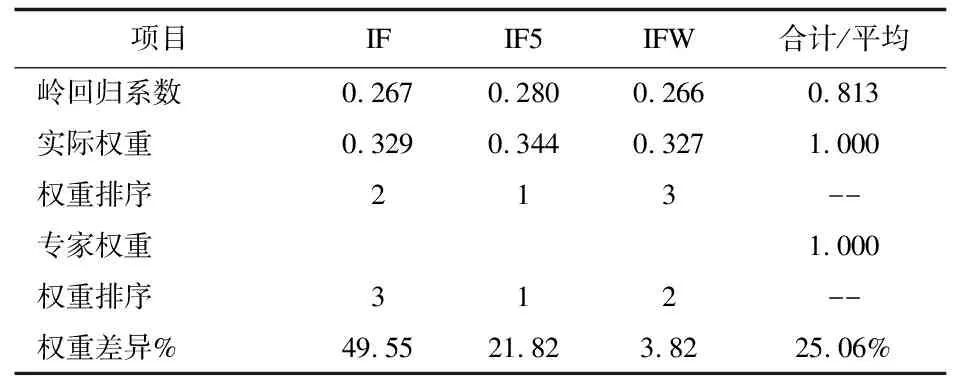
表5 高相关指标TOPSIS评价实际权重

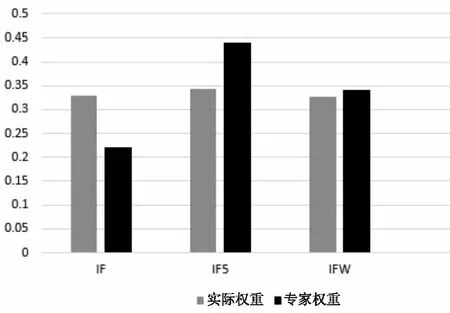
图4 高相关指标TOPSIS评价实际权重

进一步计算权重失灵度，发现专家赋权线性评价与TOPSIS评价的排序绝对总误差为86，权重失灵度为0.45，即对于高相关指标而言，由于权重失灵的存在，导致专家赋权线性评价与TOPSIS评价的排序差异仅为0.45位次，说明每个评价对象的排序误差只有不到1个位次，不同评价方法的评价结果排序具有较好的稳定性，应该说处于较高的权重失灵水平。

3.3低相关指标TOPSIS评价分析即年指标、总被引频次、特征因子、论文影响分值4个指标属于低相关指标，为了检验这4个指标单独评价对权重失灵的影响，采用这4个指标进行TOPSIS评价，并比较其与专家权重线性评价排序差异。即年指标、总被引频次、特征因子、论文影响分值4个指标的专家权重分别为0.05、0.15、0.25、0.10，转化为标准权重分别是0.09、0.27、0.45、0.18。采用专家权重线性评价与TOPSIS评价的结果如表6所示，由于篇幅所限，这里仅公布专家赋权线性评价前30的期刊。

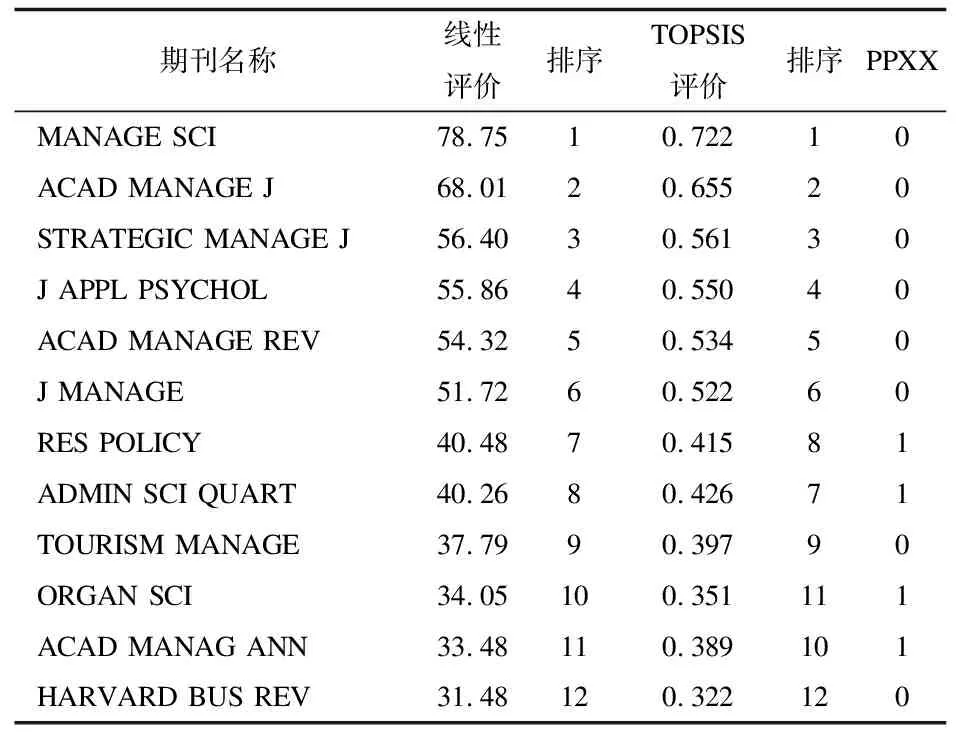
表6 低相关指标评价排序比较

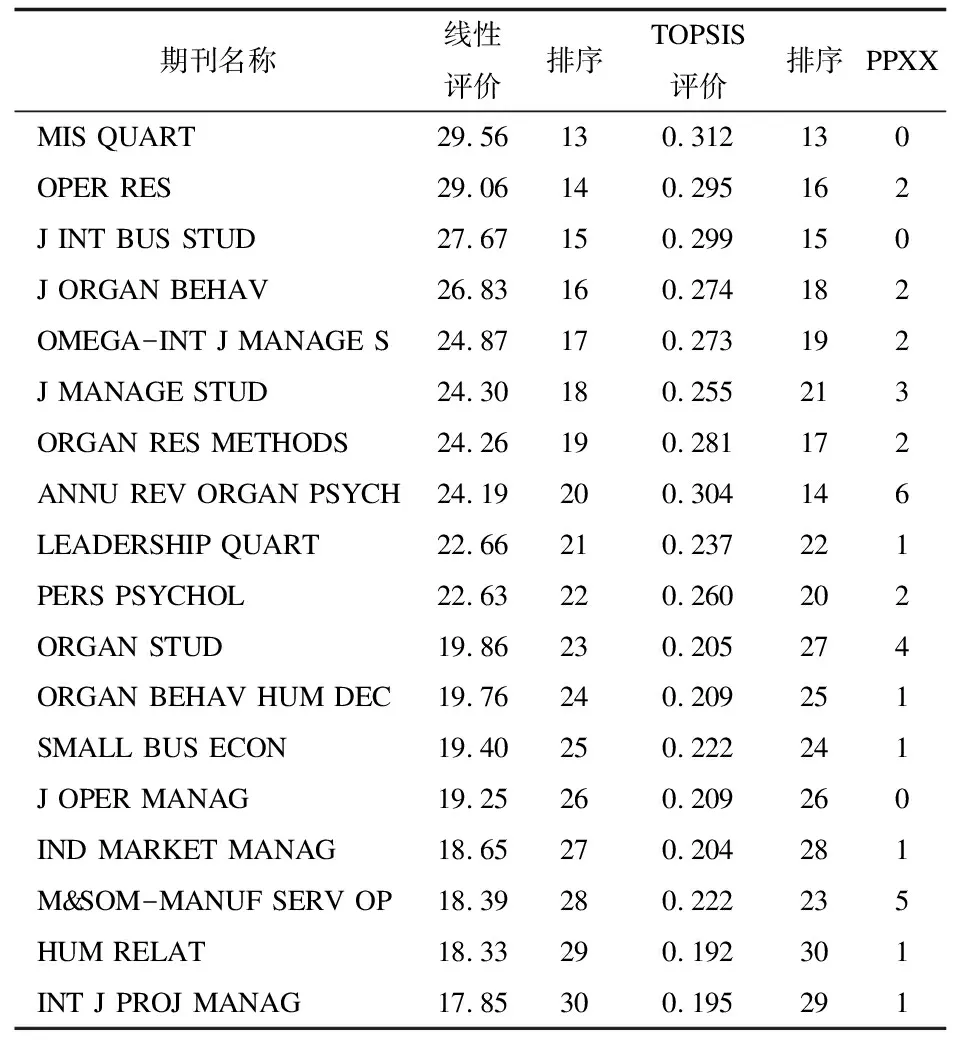
续表6 低相关指标评价排序比较

下面计算实际权重，为了降低评价指标多重共线性的影响，采用岭回归对低相关指标评价值与评价指标进行回归，当标准系数之和为0.7时，模型趋于稳定，拟合优度为0.921，具有很好的拟合效果，因此取此时的回归系数作为最终结果。

进一步将回归系数进行归一化处理，得到评价指标的实际权重，如表7所示。TOPSIS低相关指标的实际权重最大的为特征因子0.284，其次是总被引频次0.282，再次是论文影响分值0.263，最后是即年指标0.171。这个排序与专家权重大小排序基本相同，应该说这是一种偶然。此外，尽管权重排序相同，但权重依然有较大的差距，4个指标权重的平均差异为90.00%、4.44%、36.89%、46.11%，平均差异为44.36%。

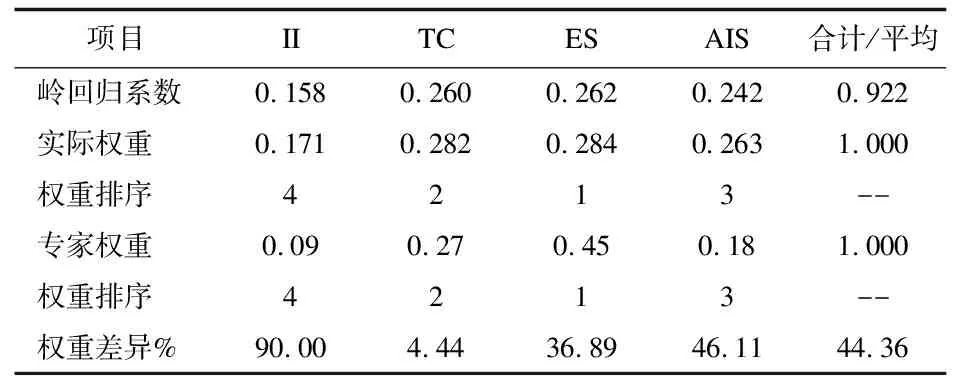
表7 低相关指标TOPSIS评价实际权重

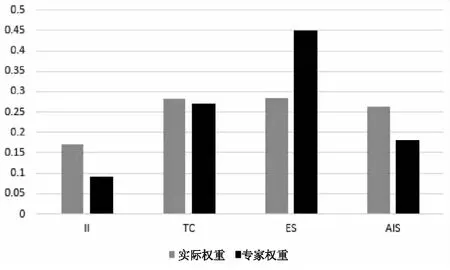
图5 低相关指标TOPSIS评价实际权重

进一步计算权重失灵度，发现低相关指标专家赋权线性评价与TOPSIS评价的排序绝对总误差为1896，权重失灵度为9.82，即对于低相关指标而言，专家赋权线性评价与TOPSIS评价的排序差异为9.82位次，应该说排序相差非常大，说明基本不存在权重失灵。

3.4全部指标TOPSIS评价分析根据表1中的专家权重，采用全部指标进行评价，专家赋权线性评价与TOPSIS评价结果如表8所示。同样为了节省篇幅，仅公布按线性评价排序前30位的结果。

下面计算实际权重，为了降低评价指标多重共线性的影响，采用岭回归对全部指标评价值与评价指标进行回归，当标准系数之和为0.74时，模型趋于稳定，拟合优度为0.942，具有很好的拟合效果，因此取此时的回归系数作为最终结果。

进一步将回归系数进行归一化处理，得到评价指标的实际权重，如表9所示。TOPSIS全部指标评价的实际权重最大的是5年影响因子0.177，其次为影响因子0.172，最小的是即年指标0.101。专家权重最大的为特征因子0.25，其次是5年影响因子0.20。权重排序相差较大，平均权重相差为45.70%，也处于较高水平。

进一步计算权重失灵度，发现全部指标专家赋权线性评价与TOPSIS评价的排序绝对总误差为738，权重失灵度为3.82，即对于全部指标而言，专家赋权线性评价与TOPSIS评价的排序差异为3.82位次，相对于高相关指标和低相关指标，权重失灵水平处于中等，说明存在轻度的权重失灵。

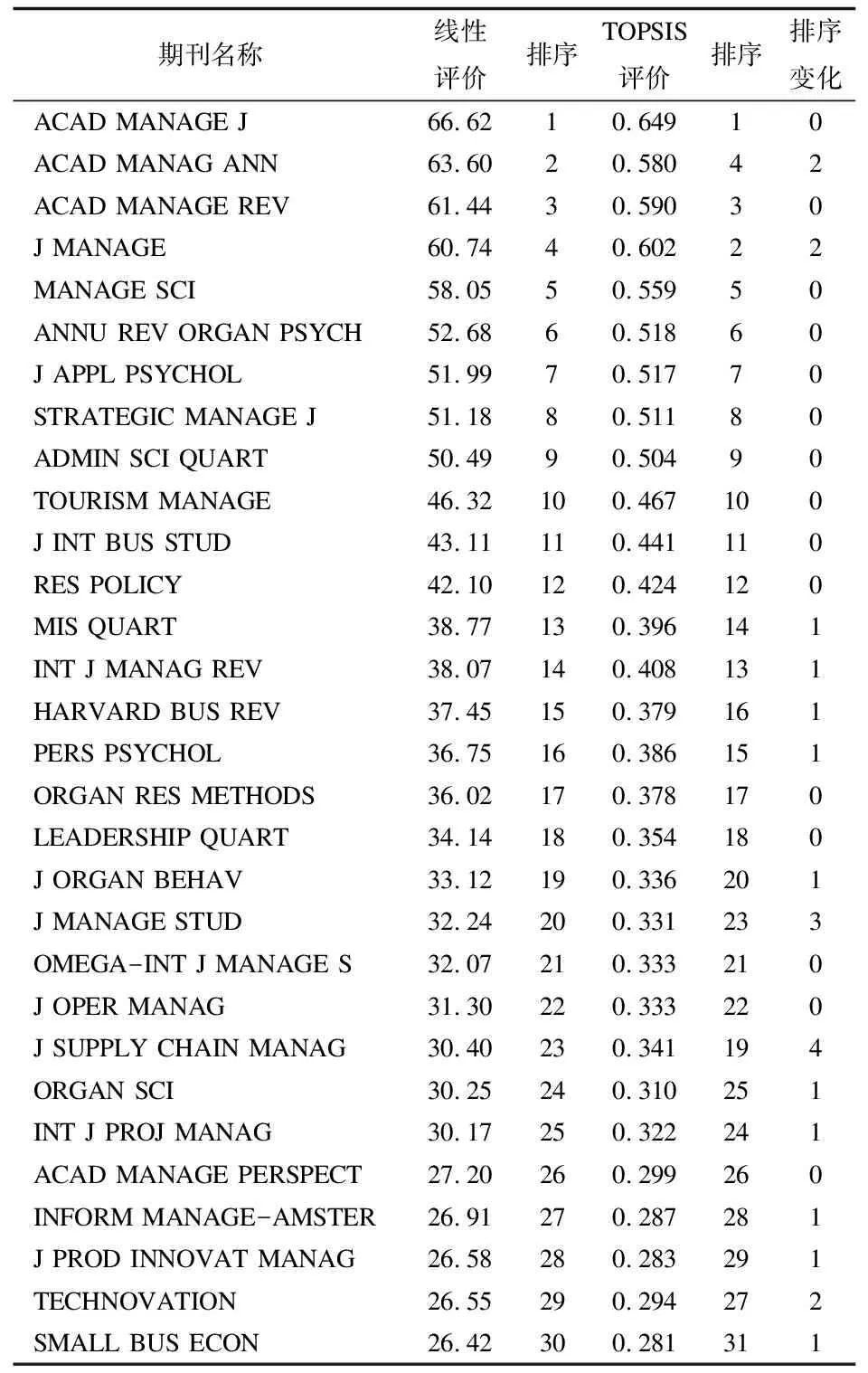
表8 全部指标评价排序结果比较

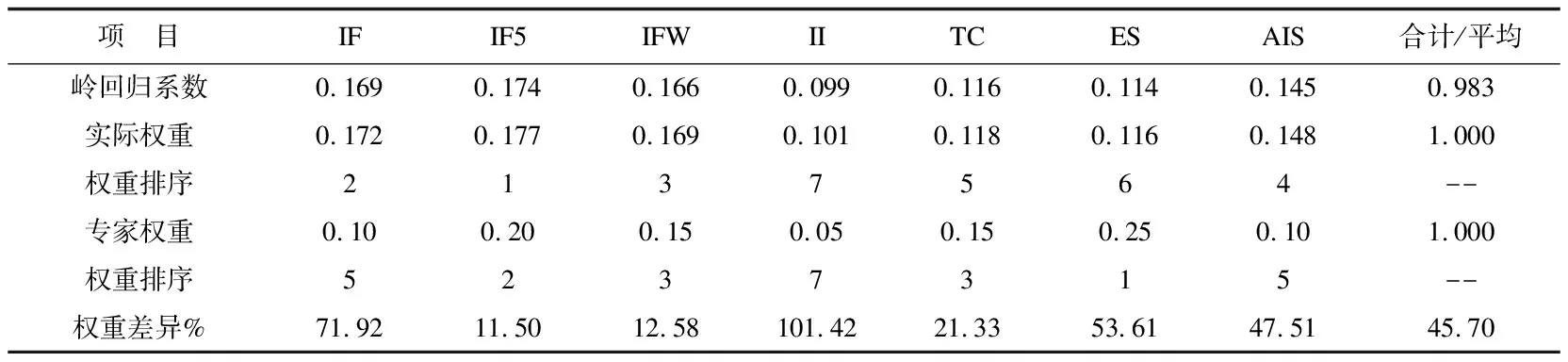
表9 低相关指标TOPSIS评价实际权重

4 结论与讨论

a.赋权类非线性评价存在伪权重与权重失灵现象。本文提出赋权类非线性评价存在伪权重与权重失灵现象，其研究方法是通过岭回归等方法计算出赋权类非线性评价中各评价指标的实际权重，将其转化为线性评价，并与专家赋权评价进行进一步比较。伪权重削弱了评价赋权(专家权重)的作用，使得评价产生较大的系统误差。伪权重受评价方法算法、评价指标数据分布、模拟权重计算算法的影响。

权重失灵是由高相关指标引起的，它的存在使得不管权重组合如何变化，评价结果排序维持大致不变。权重失灵的存在使得评价在一定条件下存在某种“惰性”，使得评价结果稳定性增强。

b.权重失灵有利于降低高相关指标的伪权重问题。对于赋权类非线性评价而言，通过实际权重的计算将其转化为线性评价，这为权重失灵和伪权重研究提供了一种新的分析框架。实证研究结果表明，对于高相关指标而言，由于权重失灵的存在，使得尽管存在伪权重问题，但评价结果的排序和专家赋权线性评价高度一致，从而有效降低了伪权重的危害。

c.对低相关指标的伪权重问题必须引起足够的重视。对于低相关指标而言，由于并不存在权重失灵问题，这样伪权重的负面作用更大，表现为实际权重与评价赋权相差较大，使得评价结果难以体现评价赋权，从而偏离了评价目的。在学术评价中，评价目的的实现非常重要，涉及科研成果评价、科技资源分配、调动广大科技人员积极性等诸多问题，因此这是要重点解决的问题。

d.权重失灵弱化了高相关指标非线性评价方法的选择。对于高相关指标而言，由于权重失灵的存在，使得在非线性评价方法选择的时候，不同的评价方法相当于其实际权重组合不同，但这些实际权重组合尽管不同，但评价结果的排序是大致不变的，换句话说，由于权重失灵的存在，使得对不同非线性评价方法的选取有较好的耐受性，这对评价总体是有利的。

e.在学术评价中应充分采取多种方法进行评价。学术评价往往是多视角的，一级指标之间往往相关性不高，此时采用赋权类非线性评价方法评价是不合适的，因为伪权重问题无法消除，因此对于不同属性指标的评价建议采用线性评价方法。而对于一级指标内部，或者二级指标内部，由于这些指标之间往往高度相关，会存在权重失灵问题，对评价方法选择不敏感，此时可以选取一些经典的赋权类非线性评价方法或其他方法进行评价。

需要说明的是，由于非线性评价方法较多，大多数非线性评价方法可以用本文的研究框架来进行分析，但也有少数非线性评价方法，如支持向量机、随机森林等，由于其评价原理比较特殊，对伪权重与权重失灵问题的研究还有待进一步探索。