基于分布式剪刀构型控制力矩陀螺的大尺寸空间结构振动抑制
2022-05-12郭川东方丽萍张景瑞李公军
郭川东,胡 权,方丽萍,张景瑞,张 军,李公军
(1. 北京理工大学宇航学院,北京 100081;2. 北京控制工程研究所,北京 100094)
0 引 言
随着对高功率通信和高分辨率观测等航天任务需求的提升,航天器的太阳翼、天线、桁架机构等柔性部件的尺寸已经由十米量级向几十米、甚至上百米量级发展。柔性部件在受外部扰动或进行姿态机动时容易产生振动,进而可能对高精度航天任务产生影响,因此需要对此类柔性部件进行主动振动抑制。传统的集中式控制策略采取在中心刚体上安装执行机构、利用中心刚体与柔性部件的刚柔耦合作用实现柔性结构振动抑制;或在柔性部件根部安装阻尼器,降低结构振动对本体姿态运动的影响。但随着航天器尺寸增大,柔性结构甚至成为系统主体,传统的集中式控制策略已经很难实现对此类大尺度柔性航天器的姿态控制和振动抑制,则必须采用分布式控制策略,在航天器上分布式安装执行机构和传感器。
角动量交换装置由于输出力矩精确、连续且不消耗推进剂,被广泛用于柔性航天器结构振动抑制。D’Eleuterio和Hughes首先提出在柔性结构上连续分布角动量交换装置来实现振动抑制和形状控制,即得到陀螺柔性体。Damaren和D’Eleute-rio最早研究了陀螺柔性体的最优控制问题及能控性和能观性问题。Shi和Damaren研究了在固支边界条件的柔性板末端安装单个CMG,基于Lyapunov方法设计了框架角的控制律,主动增加结构阻尼以快速衰减振动。Hu等假设在柔性结构上分布安装CMG,在考虑CMG动力学特性的前提下,建立了陀螺柔性体的动力学模型,并进行了陀螺柔性体的姿态控制和振动抑制。Guo等在柔性航天器上分布安装CMG,提出了一种新的基于模态力补偿器的姿态机动控制策略,抑制了挠性航天器姿态机动时的振动。贾世元等基于最优控制理论,使用遗传算法求解了CMG在约束边界柔性结构上的优化配置问题。但是,上述研究均基于较为理想的假设,并未考虑在工程中使用CMG的一些约束,例如,目前得到的CMG操纵律大都为鲁棒伪逆操纵律,在应用中会引入误差,且求解时计算量较大,会造成控制闭环中的延迟,降低振动抑制效果。
剪刀构型CMG广泛应用于航天器姿态控制及柔性结构振动抑制,由一对同步进动的CMG组成,其输出力矩方向恒定。Yang和Chang在空间桁架上安装一对剪刀构型CMG,桁架一端可绕固定转轴机动,另一端载有货物或航天员,通过设计双陀螺系统运动同步的自适应控制策略实现了桁架大范围机动。Zhou等针对上述系统,基于Lyapunov方法设计了一种自适应非线性反馈控制器,通过实现剪刀构型CMG同步驱动完成桁架机动。为了提高高超声速滑翔飞行器的突防能力,Zhao等提出了一种采用剪式控制力矩陀螺的机动控制方法,并设计了基于反馈线性化和线性二次型最优算法的解耦控制器。Jin将剪刀构型CMG安装在柔性桁架端部,设计一种改进的PD控制器实现桁架机动,同时利用自适应反馈非线性控制策略实现桁架主动振动抑制。目前在公开文献中,尚未见到使用微型剪刀构型CMG实现大型结构振动抑制方面的工作。注意到其构型简单、操纵律易设计,本文深入研究基于该构型CMG的大尺寸空间结构振动抑制,重点分析剪刀构型CMG出现的一种“死区”现象,并设计易于工程应用的操纵律。
本文章节安排如下:第1节将建立分布式安装有剪刀构型CMG的约束边界柔性结构的动力学模型;第2节将基于Lyapunov方法设计剪刀构型CMG的操纵律,以期实现柔性结构振动抑制;第3节对所设计操纵律进行分析和改进;第4节通过数值算例验证改进的剪刀构型CMG操纵律;最后,第5节将对全文作总结。
1 系统模型
具体研究对象为分布式安装有多组剪刀构型CMG的约束边界柔性结构,同组两个CMG安装在同一个平面内,其转子转速和框架转向正方向如图1所示。系统的连体坐标系为,分布安装的第组剪刀构型CMG安装平面坐标系定义为p;每组两个CMG完全相同,分别编号为,a和,b,CMG框架坐标系g,a,g,b和转子坐标系r,a,r,b原点均位于节点g。
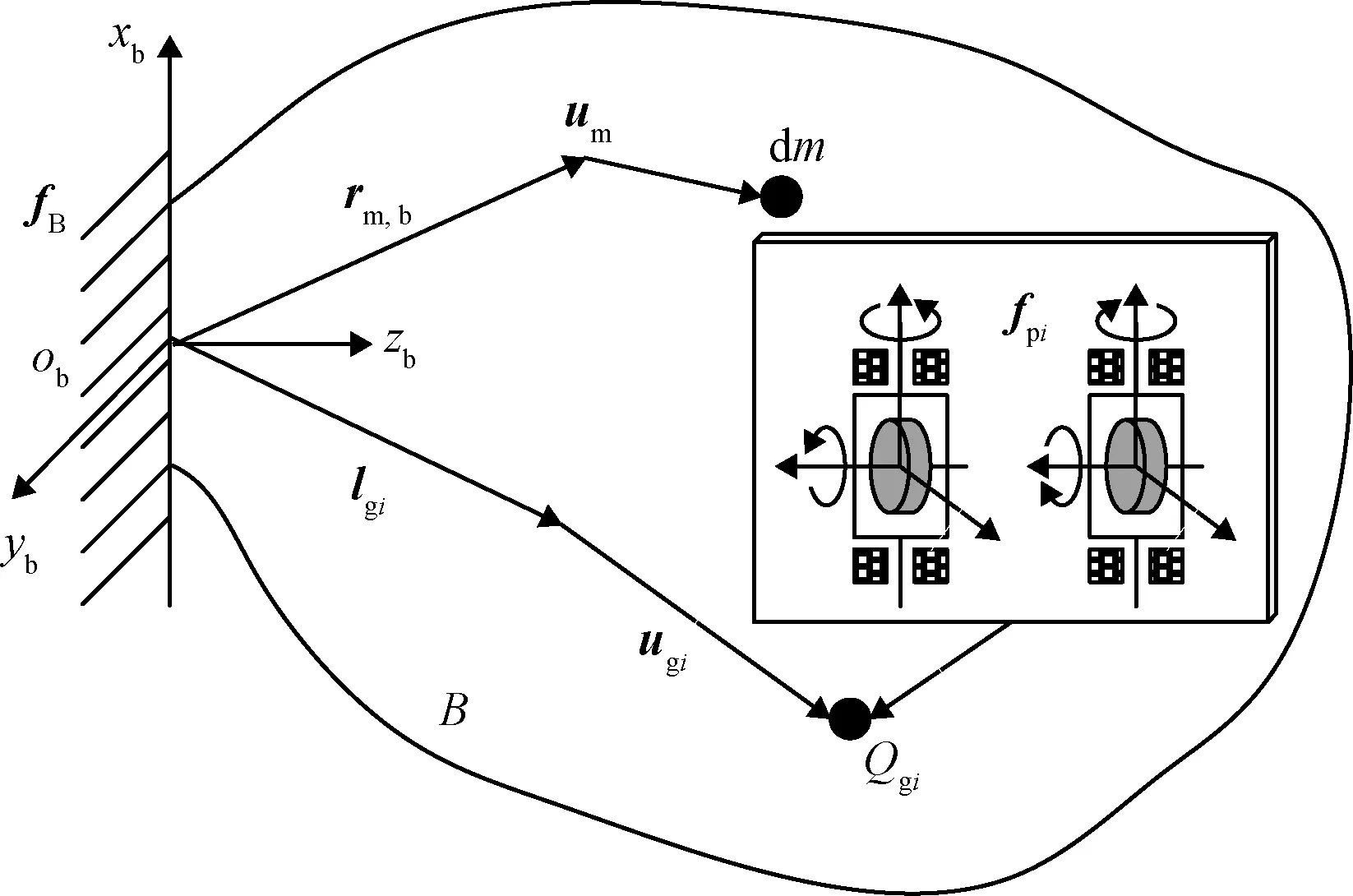
图1 安装有剪刀构型CMG的柔性结构示意图Fig.1 Flexible structure with distributed V-gimbaled CMGs
1.1 剪刀构型CMG
如图2所示,当剪刀构型CMG输出力矩时,每个CMG的框架和转子均转向相反、转速相等,则两个CMG的力矩值分别为

(1)

(2)


图2 剪刀构型CMG示意图Fig.2 Sketch of V-gimbaled CMGs
容易看出,合力矩的方向垂直图2所示安装平面,其值有

(3)
式中:为变系数,其值有
=2cos,a
(4)
式中:,a为第组剪刀构型CMG中第个CMG转过的框架角,,a∈[-180°,180°)。在框架角小角度运动假设下,可近似认为=2或=-2。由式(4)易得

(5)
1.2 动力学模型
在文献[11]和[21]中,Hu等在考虑CMG动力学特性以及CMG与柔性结构之间的相互作用情形下,推导了该系统的动力学方程。在假设柔性结构发生小范围弹性变形的假设条件下,其上质量微元d相对于的弹性变形和弹性转角采用模态展开法描述,
=
(6)
=
(7)
式中:∈3×,∈3×分别是d的平动模态向量和转动模态向量;∈×1为柔性结构的模态坐标,为用于描述柔性结构弹性变形的模态阶数。
由于研究对象为约束边界柔性结构,因此只需要考虑柔性结构的振动方程。基于文献[11]中式(7),消去方程组的高阶非线性项,并保留了CMG与柔性结构之间的相互作用,得到结构振动方程为
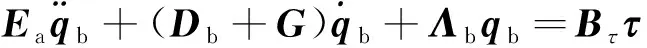
(8)
式中:∈×是一个对称矩阵,表示受CMG影响的柔性结构模态质量矩阵;∈×和∈×为对角矩阵,分别表示柔性结构本身的阻尼矩阵和刚度矩阵;∈×是一个反对称矩阵,表示CMG与柔性结构的耦合系数矩阵;是由CMG的框架转动所产生的作用于柔性结构的广义模态力,是CMG的力矩系数矩阵;=[,…,],其中是第组剪刀构型CMG的输出力矩。
这里变量,和由以下公式给出,

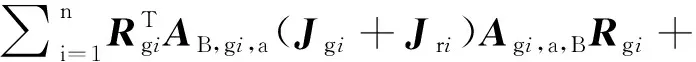

(9)
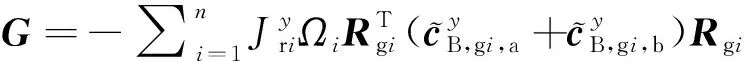
(10)
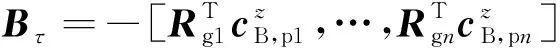
(11)

假设在柔性结构上共位安装组剪刀构型CMG和角速度计,选取为第组剪刀构型CMG力矩输出方向上的分量,由微机电系统(MEMS)角速度计测得,即有

(12)


(13)
对比式(1)与式(13)可以看出,

(14)
从式(8)可以直观看出,当需要抑制柔性结构的阶振动时,需要使用的剪刀构型CMG的数量应满足≥。当需要抑制的模态阶数较多时,所需要的CMG的数量也随之增加。利用剪刀构型CMG开展柔性结构振动抑制,适合于长杆、帆板、桁架等较为简单的柔性结构。
2 剪刀构型CMG操纵律设计
基于上一节的系统动力学模型,选取Lyapunov函数,

(15)
对其求导有,
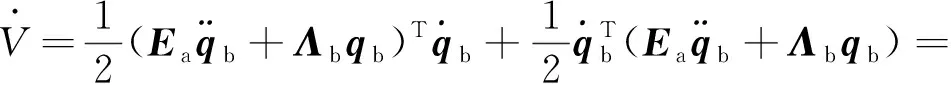

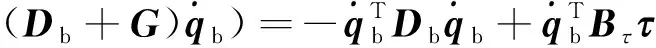
(16)
在第二步利用了的反对称性。设计角速度反馈控制律为

(17)
式中:=diag(,…,d),d>0,则有

(18)

由式(17)即有,对第组剪刀构型CMG有
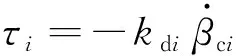
(19)
将式(3)代入式(19)可得
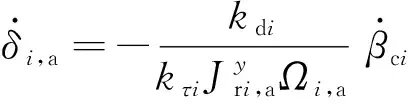
(20)


(21)
即有>0,结合式(5),则CMG操纵律修正为

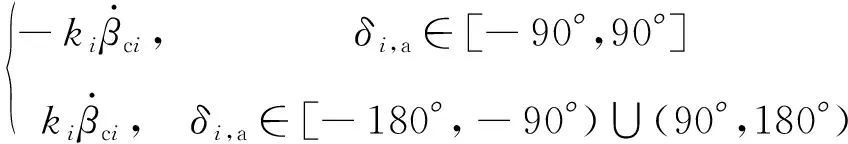
(22)
由于两个CMG的框架转向相反、转速相等,则有
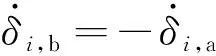
(23)
至此已经得到了在约束边界柔性结构上分布安装组剪刀构型CMG时,实现柔性结构振动抑制的剪刀构型CMG的操纵律。只需选取适当的反馈增益>0,即可保证系统的渐近稳定性。
3 操纵律分析及其改进
3.1 操纵律分析
以10 m长的柔性桁架为仿真对象,桁架质量为11.49 kg,基频为1.8238 Hz。在桁架端部安装两组剪刀构型CMG,如图3所示,两组剪刀构型CMG输出力矩均在桁架本体系的方向上。第一组剪刀构型CMG安装在桁架端部,用于演示式(22)和(23)所示操纵律,抑制桁架在方向上的振动;第二组剪刀构型CMG安装在距离桁架端部0.5 m处,用于激励方向上的振动,单个CMG的质量约1.25 kg、转子角动量为0.3 N·m·s,框架角速度最大幅值为90(°)·s。不考虑CMG内部的摩擦和力矩“死区”等问题。挂载CMG后桁架基频降低至1.1459 Hz。

图3 CMG安装示意图Fig.3 Sketch of V-gimbaled CMGs locations
第二组剪刀构型CMG驱动采用正弦激励规律,即
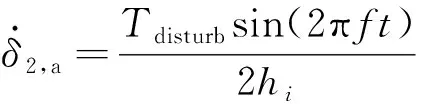
(24)
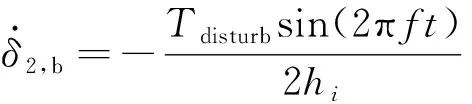
(25)
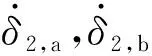
在仿真中,前10 s对桁架施加激励,不施加主动控制,此时参数选择为=01 N·m,=116 Hz;10 s后激励结束,采用式(22)和(23)的操纵律开始施加主动振动抑制,设置控制增益=800。为了避免框架轴电机长期高速驱动,设定框架轴的最高转速为57.3(°)·s。在工程试验过程中,CMG按设定的操纵律工作,发现在试验最开始的一小段时间内,CMG存在启动延迟。为了考察CMG在较为极端情况下的工作能力,并重现工程试验中的启动延迟现象,在操纵律分析过程中,假设初始时第一组剪刀构型CMG工作在“零力矩”状态,即=90°,=-90°。
桁架端部中心点位置如图3所示,以桁架端部中心点在桁架本体坐标系下的变形作为考察桁架变形量的依据。经过20 s仿真,得到桁架端部中心点的变形情况,如图4所示。可以看出,自第10 s振动抑制开始后,端部中心点变形并没有按期望变小,而是出现了异常的增大;桁架振动抑制的效果并不明显。
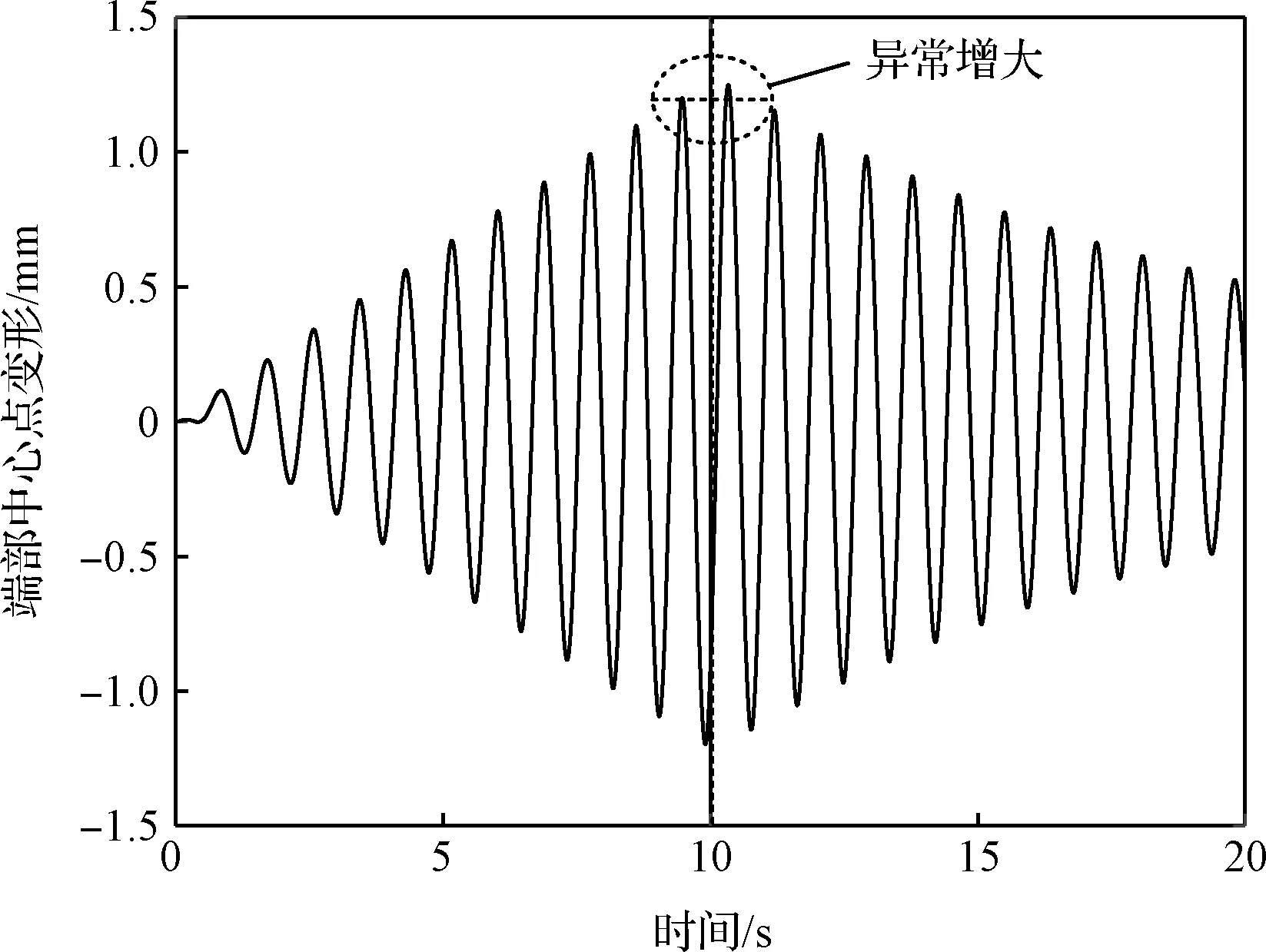
图4 桁架端部中心点变形(振动抑制效果不明显)Fig.4 The deformation of the center point on the end of the truss (poor vibration suppression effectiveness)
第一组剪刀构型CMG框架轴运动规律如图5所示,可以看出,在10 s~10.3 s,短短0.3 s时间内,框架轴运动方向进行了数十次切换,进入一种类似“死区”的状态。这种短时间内的密集切换,在工程上难以实现,也是在工程试验过程中出现CMG启动延迟的原因。在工程试验过程中,这种情况持续的时间会更长,严重影响振动抑制的效果。

图5 第一组CMG框架角速度(振动抑制效果不明显)Fig.5 The gimbal angular velocity of the first pair of CMGs used for vibration suppression (poor vibration suppression effectiveness)
为深入分析“死区”产生的原因,绘制10 s后第一组剪刀构型CMG安装位置处MEMS角速度计测量值、第一组剪刀构型CMG中号CMG的框架角速度以及号CMG的框架角度的三维曲线,如图6所示。图中深色曲线(黑色虚线框圈出)为“死区”状态下的曲线,浅色曲线(右上)为CMG正常工作时的曲线。可以明显看出,“死区”状态出现在角速度计测量值为负值的时候,此时框架角在90°附近摆动;在“死区”状态下,当框架角大于90°时,框架角速度为负值,此时框架角减小;当框架角减小至90°以下时,框架角速度切换为正值,此时框架角增大。框架的运动陷入“死区”循环。当角速度计测得的值转为正值时,框架轴运动才脱离“死区”,但框架轴脱离“死区”后并未取得较好的振动抑制效果。结合式(22)可知,式(22)给出的CMG操纵律为分段函数形式,存在-90°和90°两个分段点,“死区”出现在分段点附近。

图6 第一组CMG框架轴运动分析Fig.6 Analysis of gimbal motion of the first pair of CMGs for vibration suppression
该仿真工况较好还原了工程试验中出现的启动延迟现象,也能解释启动延迟出现的原因,有助于开展操纵律的更新设计。
3.2 避“死区”操纵律设计
为了使框架轴运动能快速转出“死区”,对剪刀构型CMG操纵律作出调整,设计一种避“死区”操纵律,如图7所示。
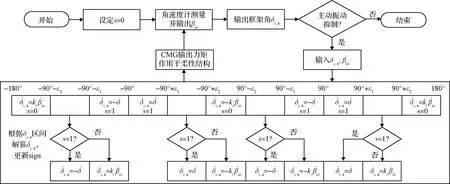
图7 应用避“死区”操纵律实现柔性结构振动抑制流程图Fig.7 Flow chart of vibration suppression for flexible structures by applying “dead zone avoidance” steering law
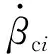
4 仿真校验
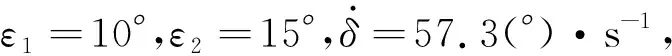
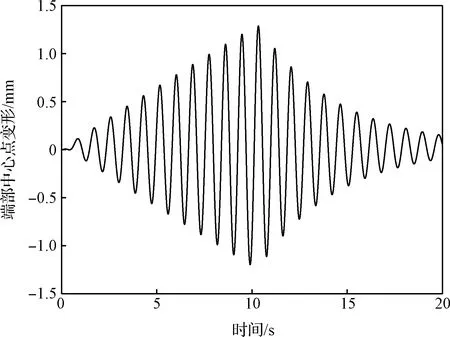
图8 桁架端部中心点变形Fig.8 The deformation of the center point on the end of the truss
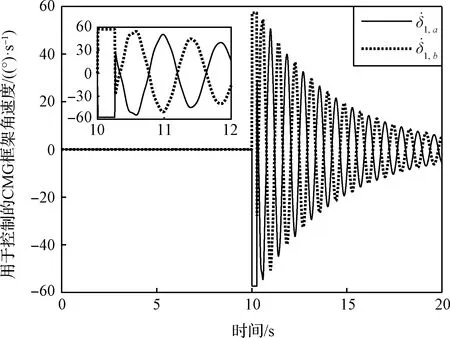
图9 第一组CMG框架角速度Fig.9 The gimbal angular velocity of the first pair of CMGs used for vibration suppression
框架角的运动曲线如图10所示,可以看出,振动抑制开始之后,CMG框架角快速运动到(-75°,75°)区间内,即图7中的(-90°+,90°-)区间,实现了持续地输出振动抑制力矩。
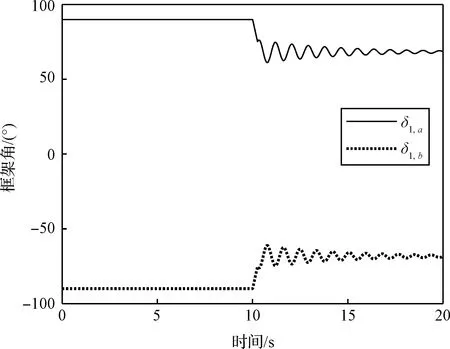
图10 第一组CMG框架角运动曲线Fig.10 The gimbal angular of the first pair of CMGs used for vibration suppression
同时模拟了10 s激励结束后不施加主动振动抑制的情形,得到不施加主动振动抑制时端部中心点变形情况如图11所示,对比图8施加主动振动抑制时的结果,可以看出利用剪刀构型CMG很好地实现了柔性结构的主动振动抑制。

图11 无控时桁架端部中心点变形Fig.11 The deformation of the center point on the end of the truss without active vibration suppression
5 结 论
本文以约束边界空间柔性结构为研究对象,在结构上分布安装剪刀构型CMG,通过建立系统动力学模型,基于Lyapunov方法设计了剪刀构型CMG的框架轴操纵律。以单部10 m长的柔性桁架为仿真对象,在桁架上安装两组剪刀构型CMG,一组用于激励桁架产生振动,另一组应用所设计控制方法进行振动抑制仿真。在仿真中发现所设计的操纵律存在“死区”问题,进而改进了所设计框架轴操纵律,设计了一种可避“死区”的操纵律。仿真结果表明,所设计避“死区”操纵律可以较好实现桁架振动抑制,且改善了振动抑制的性能。
值得注意的是,在柔性结构上安装CMG,会增加结构质量、降低结构频率。针对这一问题,可以在两方面开展进一步研究:一方面,研发集成化、小型化的CMG;另一方面,赋予CMG更多功能,如利用CMG内部的高速转子进行能量存储,同时通过CMG框架转动输出分布式控制力矩用于柔性结构振动抑制,从而减轻系统中能量存储系统的质量,可进一步弥补在柔性结构上安装CMG带来的质量增加,同时降低对CMG微型化的要求,获得更大的可靠性。
