面向不同雷达任务的认知波形优化综述
2022-05-11余若峰杨威付耀文张文鹏
余若峰,杨威,付耀文,张文鹏
1 引言
现代雷达系统通常具备执行不同雷达任务的能力,包括检测、跟踪、识别和成像等. 对于不同的任务,系统所需要的环境和目标信息是不同的. 体制上,主要采用接收端与发射端各自独立工作的开环模式,即发射端发射的电磁信号采用预先设计的波形,接收端接收回波数据并经由一系列算法提取感兴趣的信息,以此对目标和环境进行感知. 这种开环工作模式导致目标及环境信息只能从外界单向流入接收端,使得系统性能十分依赖接收端的自适应处理算法. 即使面对固定的探测场景,精心设计的波形和自适应算法(如恒虚警检测、空时自适应算法和贝叶斯滤波等)也难以保证总是能有效应对非均匀、非平稳的复杂动态环境.Gini 等[1]指出目标和环境先验知识(如目标的运动特性、环境的统计特性)的不充分利用或缺失都会极大约束雷达的探测性能. 近年来,数字任意波形发生器、信息超材料、高速信号处理芯片等先进硬件技术以及人工智能、博弈论、最优化理论等先进算法和信号处理相关基础理论的发展,有效促进了智能化雷达概念构想的提出和发展.
在自然界中,蝙蝠天生具有“回声定位”系统,能够在复杂环境中完成对猎物的搜索定位、选择跟踪、攻击捕获. 研究发现[2],蝙蝠通过主动调整定位信号的强度、方向、频率和持续时间等参数,以适应不同生活环境和不同传感任务,满足对环境的感知需求. 借鉴蝙蝠的认知过程,2006 年Simon Haykin[3]提出了认知雷达(Cognitive Radar,CR)的基本概念和结构,他认为认知雷达是一种知识辅助的全自适应系统,在接收端自适应处理的基础上,引入发射端到接收端的物理闭环反馈机制,利用雷达的回波数据完成对目标和环境的智能化交互和分析,并将系统所需的知识动态反馈到发射端,实时优化发射波形,实现对目标和环境的最佳探测性能. 这种闭环迭代的方式有效提升了雷达系统对动态环境的适应能力和对信息探测的自组织能力,因此认知雷达被认为是智能化雷达的初步探索.
2017年,Chris Baker和Hugh Griffiths率先将认知雷达的正式定义纳入IEEE 标准雷达定义中,他们认为认知雷达应当能够根据环境和目标场景的变化完成自适应操作和处理,在一定程度上体现雷达系统的智能化特征. 与自适应雷达相比,认知雷达能够在较长一段时间内对发射和接收端参数的自适应配置策略进行学习. Gurbuz 等[4]结合Fuster 对认知心理学的阐述和定义,提出认知雷达应当具有至少以下3 种机制:感知-执行循环(Perception-Action Cycle,PAC)机制、注意力机制和语言机制. 其中,PAC 机制是认知雷达收发闭环反馈的框架;注意力机制则为认知多功能雷达提供资源调度的关键信息基础;语言机制为认知雷达的数据编码提供有效框架,包括存储、通信以及不同传感器间的交互. Horne 等[5]基于规划复杂度、决策机制复杂度和记忆复杂度这3个维度,提出一种针对认知雷达的认知层次复杂度分级方案,并以此作为认知雷达设计的指导,如图1 所示. 黎湘[6]则将认知雷达的关键技术归纳为4个方面:场景感知与描述、波形最优化技术、自适应机制以及自治操作与管理机制.
认知雷达在发展过程中至少存在3 个方面的问题[7]:(1)如何建立复杂环境的数学模型以满足认知雷达系统设计的要求;(2)如何实现基于目标和环境信息的雷达认知发射;(3)如何实现基于目标和环境信息的雷达认知接收. 其中,认知发射是认知雷达显著区别于传统自适应雷达的最大特征.Gini和De Maio[8]指出,发射波形决定雷达系统的许多性能,良好的波形将使系统获得良好的探测性能,包括但不限于良好的距离和多普勒分辨率、在低峰值功率条件下获得高信号能量、能够有效利用频谱、具有较高自由度、有助于应对电子对抗干扰等. 通过认知发射,认知雷达可以针对不同环境下的不同探测任务,充分利用接收端和动态知识库中获取的先验知识和推理结果,对发射波形进行自适应优化,从而提升接收回波质量和雷达整体探测性能.
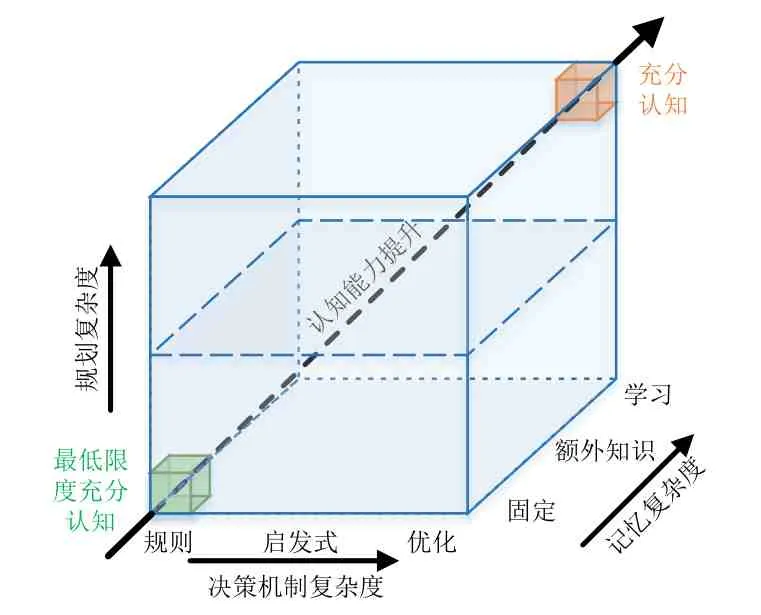
图1 Horne提出的认知雷达的认知层次分级方案
认知发射一般通过波形分集(Waveform Diversity,WD)技术实现. 波形分集也称为波形多样性,其概念由美国空军研究实验室传感器理事会的Michael 在2002年首次提出. 作为一种遥感范式,波形分集的基本要素大致上可以分为测量分集、知识辅助处理与设计和发射自适应[9].2017 年IEEE 雷达标准同样给出了波形分集的最新定义:根据特定场景和任务,动态自适应地对雷达波形进行优化,以最大限度地提高雷达系统的探测性能. 这种自适应的特性可以体现在不同的优化域中,包括天线辐射方向图(发送和接收)、时域、频域、编码域和极化域等,具体表现为波形的空间分集、时间分集、频率分集、极化分集等.
自认知雷达概念产生以来,涌现出了大量的优秀研究成果,Gurbuz[4]全面总结了2003 年至2019 年间以“认知雷达”为主题的工作中不同研究方向的分布情况. 他指出尽管认知雷达系统架构、阵列天线资源调度和控制、自适应射频元件的设计和实验测试等方面也有相关的探索,但目前绝大部分工作的研究重点仍集中于认知波形优化. Blunt[10]则从波形分集的角度,对近年来在波形优化设计方面取得的成就和主要研究思路进行了阐述. 国内方面,崔国龙[11]综述了不同干扰环境、目标模型和天线配置等因素对认知波形优化的影响. 王璐璐[12]则针对雷达检测任务的认知波形优化进行了深入的探讨.
聚焦于面向检测、跟踪、成像、分类任务以及抗干扰的认知波形优化方法,本文对相关技术的发展脉络进行了梳理,以期为未来的研究提供参考,主要贡献有以下2个方面:
(1)分别从检测、跟踪、成像、分类以及抗干扰的角度,总结了面向单一任务的波形优化准则和方法,梳理了相应的研究进展,为面向单一雷达任务的波形优化研究提供了纵向的对比视角;
(2)从雷达任务间的耦合性出发,简要分析了面向联合多任务波形优化的必要性和可行性,梳理了相应的研究进展,为面向联合多任务的认知波形优化研究提供了横向的对比视角.
2 认知波形优化基本框架
不失一般性地,雷达波形可以由一个有限维参数向量θk描述,θk每一维元素对应一个参数变量(自由度)且各维参数之间通常满足正交性,θk的可能取值构成有限维欧几里得空间的一个子集,称为θk的参数空间. 基于波形分集范式的认知波形优化基本框架,通过构建满足系统性能指标的目标函数,在参数空间中搜索寻优,在线选择符合特定任务需求的波形参数θ̂k. 根据参数空间的离散与否,认知波形优化可以进一步细分为最优波形选择和最优波形设计[13]. 尽管在理论上最优波形设计具有更高的灵活性,但是受当前阶段发射端硬件设备和接收端信号处理单元的限制,现实系统中往往难以实现.
上述框架中,认知波形优化可以等价表示为一个多维多约束的目标函数求解问题,如式(1)所示:
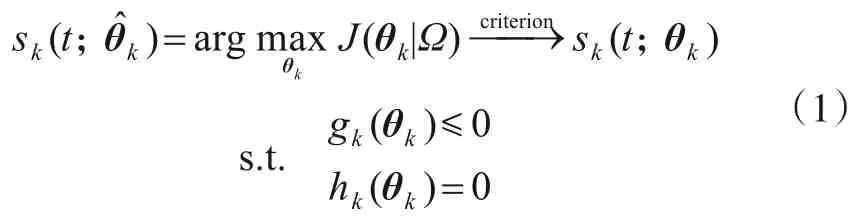
其中,J(θk|Ω)是目标函数,其形式通常与选取的优化准则和雷达系统实际应用任务、工作模式相关;sk(t;θ̂k)在指定优化准则(criterion)下最优波形sk(t;θk)的近似或估计;Ω是先验知识的集合,包括目标和环境特性等与雷达波形相关的先验知识;gk(θk)与hk(θk)分别为波形参数的不等式约束和等式约束.
2.1 优化准则与约束条件
不同雷达任务对目标和环境信息的需求不同,根据系统的主要任务和工作模式,使用的优化准则及相应的目标函数也不尽相同. 面向特定任务时,优化准则和目标函数通常与任务的性能指标是直接或者间接相关的[11]. 例如,从统计信号处理的角度看,检测和分类任务主要是利用目标和噪声、杂波或者目标和目标之间的统计特性差异进行区分的. 因此,各类距离测度指标均能够用于评价任务性能. 而从估计理论的角度看,跟踪和成像任务可以利用各类估计误差指标对任务性能进行评价.
此外,需要注意不同雷达任务之间存在的耦合性[14],如图2 所示. 例如,对于目标分类和目标跟踪任务,目标分类结果可以辅助目标跟踪算法的建模以及提升目标跟踪的性能,而目标跟踪结果反过来可以作为目标的行为特征辅助目标分类算法;对于目标检测与目标分类任务,目标分类属性可以用于检测算法的建模,而目标检测结果反过来会影响分类算法的性能;对于目标检测与目标跟踪任务,检测算法的精度限制了跟踪算法的性能,而跟踪结果反过来可以辅助目标检测算法. 因此,在选取优化准则或者评价指标时应当结合雷达任务的具体应用背景,在某些条件下,不同优化准则之间可能是等价或者包含的关系.
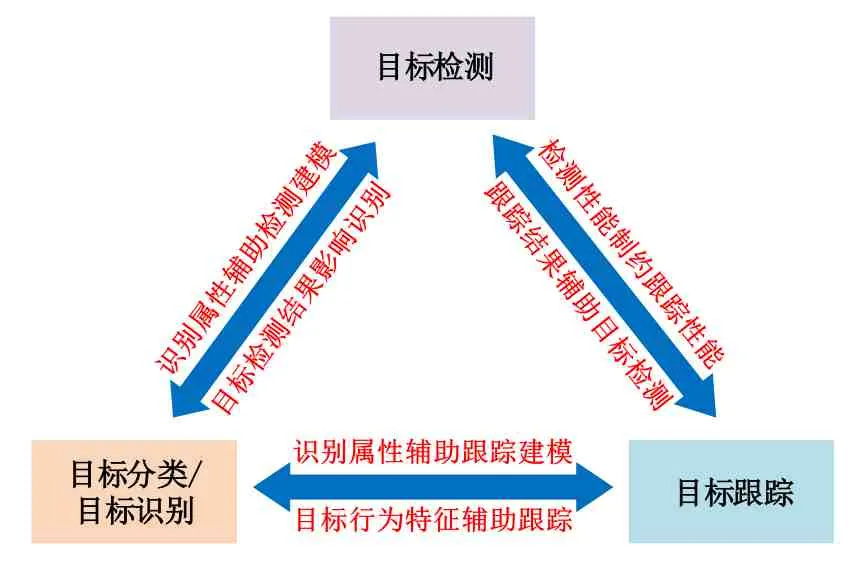
图2 雷达任务耦合性示意图
为了避免出现优化波形在物理上不可实现或者缺乏明确物理内涵的问题,通常需要在一定的系统限制条件下完成[13]. 约束条件的选取同样影响最终波形的性能、优化过程的难易程度以及优化执行效率. 常用的约束条件主要有发射信号总能量约束、发射信号时间长度约束、发射信号有限带宽约束(近似约束,有限带宽会导致时域信号无限长)、发射信号幅度约束、雷达的分辨率和压缩旁瓣水平约束、模糊函数性能约束、频谱兼容性约束等. 其中,频谱兼容性约束,也被称为“频谱塑形”,实用系统在复杂的电磁环境中要避免被干扰或者干扰其他设备,需要将发射频谱约束在允许的频带内,频带外具有高的衰减或高的衰减速率. 在极端情况下,允许频带内甚至可能仅存稀疏的可用频点.
通常不必要的约束条件会导致优化问题求解过程十分复杂,甚至无法求解,优化效率低下. 系统一般要求实时求解最优波形,使波形优化过程能够在较短的时间(例如一个脉冲周期)内完成[15],这对波形优化算法的效率提出了很高的要求. 而且,在满足系统需求的前提下,对严格的约束条件进行松弛或者等价转换,有时也能够得到令人满意的结果. 例如,在恒模约束下进行波形优化时,可以直接对波形的相位进行编码设计,尽管减少了设计自由度,但提高了计算效率,而且可以得到具有较大发射功率的信号和接近最佳的优化增益.
作为波形的一种通用评价工具,模糊函数一方面可以用作优化准则,一方面也可以在其他准则下对波形进行约束. 其最显著的功能是用于衡量距离分辨率和距离旁瓣水平,因为距离分辨率反映了发射波形能够区分2个具有相同多普勒目标的最小间距,而距离旁瓣水平则表征了一个散射点对其他具有相同多普勒散射点的影响,评价波形旁瓣水平的约束条件有峰值旁瓣比(衡量最坏条件下旁瓣响应的度量)、积分旁瓣比(旁瓣水平的聚合度量)等. 表1 总结了在主流应用中不同雷达任务波形优化的优化准则和约束条件.
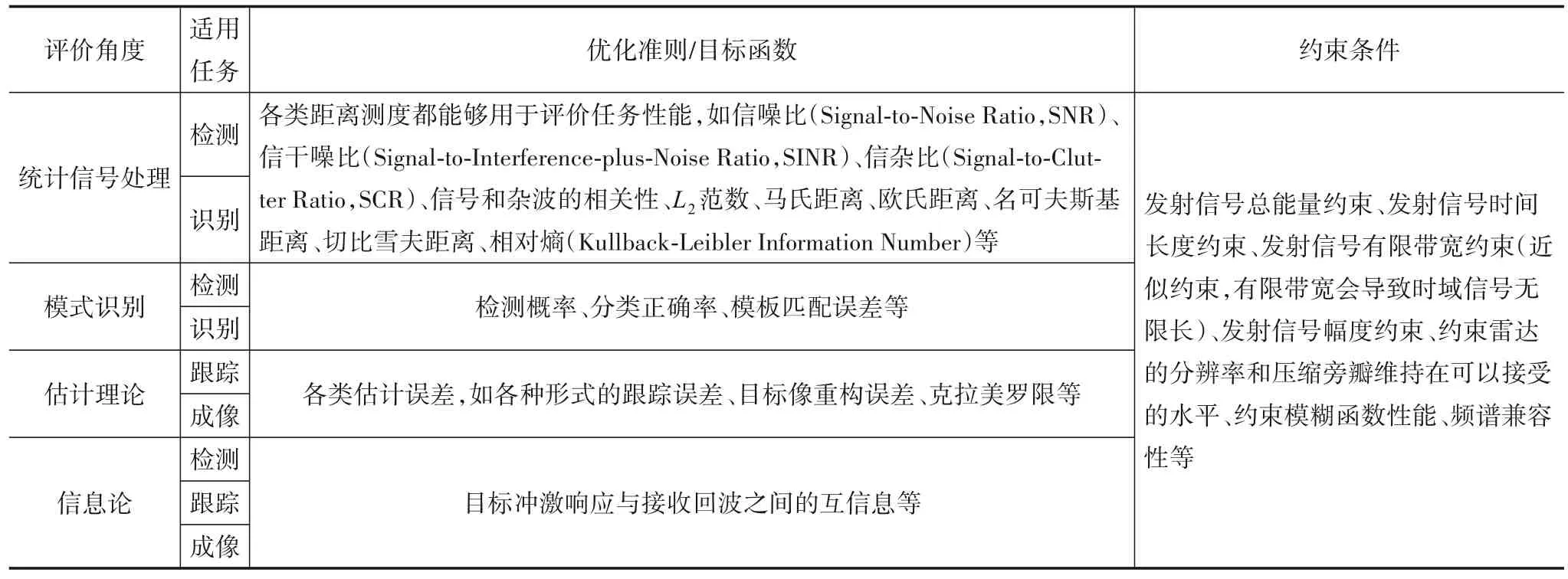
表1 不同雷达任务波形优化的优化准则和约束条件
2.2 求解方法
在上述波形优化框架中,可以利用优化理论求解由目标函数表示的优化问题,得到相应的最优波形. 根据波形定义域的不同,主流方法的求解对象大致上可以分为最优波形的频域表示和时域表示两大类.
除范梅梅[6]提到适用“特征值法”和“注水法”的场景外,多数应用的目标函数和约束条件具有比较复杂的形式,可能会引入多目标优化(需要同时满足多个目标函数,Multi-objective Optimization Problem,MOP)、多峰优化(目标函数的非凸性)及组合优化等问题,使得认知波形优化变得难以求解[16]. 并且在求解过程中,除了需要避免陷入局部极值,还要兼顾计算效率. 当前研究工作中,采用具有全局搜索能力的随机进化算法,如遗传算法(Genetic Algorithm,GA)[17]、粒子群算法[18],但一般不能满足对计算效率的要求. 而以投影梯度法[19]、拟牛顿法为代表的梯度寻优算法有着更高的计算效率,但是不能够保证结果的全局最优性. Majorization-Minimization(MM)算法为一些无法直接求解的复杂优化问题提供了一种类似于动态规划的解决方案,其基本思想是将问题分解为一系列结构简单的近似目标函数,再依次进行解决[20]. 受到生物种群启发的智能优化算法也是一类求解优化问题的有效工具,主要包括以差分进化算法和免疫算法为代表的进化类算法,以蚁群算法、鸟群算法为代表的群智能算法,模拟退火算法,禁忌搜索算法,以及包括经典后向传播算法的神经网络算法等. 另外,在系统允许范围内,通过某种方式实现条件松弛,将非凸优化转化为凸优化,通过相对简单的优化算法亦可获得最优解.
目前的主流工作中,多数算法仅给出了最优波形频域表示,但最优波形的频域表示不能直接由雷达发射端进行传输,需要首先合成(synthesis)相应的时域波形. 然而,最优波形的频域表示缺失了相位信息,直接使用逆傅立叶变换综合时域波形,需要首先构造随机的相位谱,由此得到的时域波形还存在至少两方面的问题:一方面是有限带宽约束导致的无限时长,另一方面是有限能量不足以约束波形包络. 因此,必须考虑对信号的相位进行恢复,尽管Patton[21]对相位恢复算法的计算效率和求解结果的质量进行了深入研究,但仍没有在本质上解决幅度调制的问题.Kay[22]提出可以通过Durbin 法合成具有最小相位的时域信号,然而该方法会使信号能量主要集中在低时延区间,而信号后端幅度较小,整体呈现较大的起伏.
考虑恒模约束时,经典的时域波形综合方法主要有驻点相位法(Stationary Phase Technique,SP)和迭代传输法(Iterative Transform Method,ITM)[23]等. 驻点相位法的基本假设是复信号的大部分能量都集中在某个驻点附近. 因而可以通过调整信号不同频点分量的持续时间来控制该分量在整个信号中的幅度. 换句话说,使信号频率分量的持续时间与该分量的频谱幅度成正比. 基于驻点相位法得到的综合波形在阻带内与最优谱是不一致的,因而该方法仅适用于具有平坦谱的波形相位恢复. 迭代传输法是一类迭代寻优方法,其有效性被认为是由交替投影(Alternating Projections,AP)性质[21]带来的.Gerchberg-Saxton[24]最早提出基于迭代传输思想的相位恢复算法,具有无需设置先验参数的优点,且在计算复杂度更低的前提下,具有与梯度下降法相近的性能.ITM 可以通过多次迭代逼近最优谱,近似程度与迭代次数成正比,但是由于优化问题本身的非凸性,不能保证总是收敛到最优解.
3 面向雷达任务的认知波形优化
对于雷达系统,根据对目标认知层次的不同,通常可以将感知任务进一步细分为检测、跟踪、成像、识别等,本节针对上述雷达任务以及抗干扰五个方面,从不同优化准则的角度对波形优化方法和近年来的研究进展进行梳理.
3.1 面向检测任务的波形优化
目标检测是指通过判断给定的雷达测量值来源于目标或者干扰/噪声,对目标的存在性进行判决的过程,是雷达信号处理最基本的功能之一. 利用统计信号模型描述干扰和目标时,目标检测任务可以等效为一个二元统计假设检验问题,其中最普遍的检测逻辑是阈值判别原理,即检测器通过将雷达回波测量数据与检测门限进行比较:

其中,H0是零假设,表示测量值仅为干扰;H1是备选假设,表示测量值为干扰与目标回波叠加,Γ(zk)表示k时刻关于zk的统计量;p(zk|∙)为测量数据的似然函数. 由于发射波形、目标模型、杂波干扰特性、信道噪声性质包含了相互关联的时变参数,使得zk与k时刻雷达发射波形参数θk相关. 当目标与噪声的统计特性差异越大时,越容易正确判断测量是否来源于目标. 由于目标的统计特性通常是时变的,如果雷达发射端可以在一定优化准则下根据目标和环境的变化在线设计并发射相应的波形,系统的杂波抑制效果和目标检测性能都将得到提升. 通过发射波形优化抑制噪声、杂波、干扰,以提高目标检测性能的思想最早可以追溯到1965 年Van Trees[25]提出的方法.2016 年,王璐璐[12]依据不同的目标和环境建模方式,对面向雷达目标检测任务的波形优化方法进行了详细的综述.
面向检测任务的雷达波形优化作为研究热点,受到了许多学者的关注和研究,是相关领域中成果最为丰富的研究方向之一,本节主要从SNR 准则与信息论准则的角度介绍当前的研究进展,并简要讨论近年发展起来的机器学习波形优化方法.
3.1.1 基于SNR准则的检测波形优化
检测概率是目标检测性能最常用的评价指标之一,而检测概率与回波信号的SNR 密切相关. 因此,SNR 准则也是雷达检测任务中常用的波形优化准则.通过建模杂波和干扰对回波信号的影响,上述准则可以进一步扩展到更为一般的SINR、SCR、SCNR 等(本节后续内容在不致混淆的情况下,对以上概念不再进行区分).
Delong[26]和Ares[27]在早期工作中提出杂波背景下联合设计发射波形和接收滤波器可以提升目标检测性能的思想. 尽管Sibul[28]认为,同时对信号和滤波器进行设计是没有必要的,因为在Neymen-Pearson(NP)准则下,最优接收滤波器仅依赖通道功率谱密度(Power Spectral Density,PSD)、环境杂波/噪声功率谱密度、目标运动引入的多普勒频移和发射信号的功率谱,其中唯一可控的只有发射信号的功率谱[29].
(1)联合发射波形与接收滤波优化
当前,联合发射波形与接收滤波优化是检测波形优化的一个重要研究方向. 这种方案通常利用有限信号能量和有限信号时宽约束. 在连续时间信号表示时,其最优解可以通过使用特征迭代法,求解Fredholm 积分方程的特征函数获得;在离散信号表示的情况下,最优波形为目标自相关矩阵最大特征值对应的特征向量. 结合实际应用背景,在此基础上,先前研究工作以引入幅相调制方式[30]、包络恒模[31]等约束条件或考虑最优波形的实现误差[32]、量化误差[33]等情形的误差分析为主.
Pillai[34]研究了存在信号相关干扰条件下的联合发射波形与接收滤波优化问题,给出该问题的经典信号模型,如图3 所示. 他通过形式化建模的方法推导了基于SNR 准则的发射波形和接收滤波器闭合表达式,并提出一种迭代方法以求解具有有限持续时间的发射波形和接收滤波器对. 但该算法并不能总是收敛到全局最优解[22]. Romero[35]分别对确知目标(Known Determi‑native Target)和随机目标(Stochastic Target)冲激响应条件下的信号模型进行了描述,并推导了相应的基于SNR 准则的波形优化方法. 本质上,图3 所示模型均适用于确知目标和随机目标. 本节根据Romero 的工作,首先对该信号模型进行简要介绍.
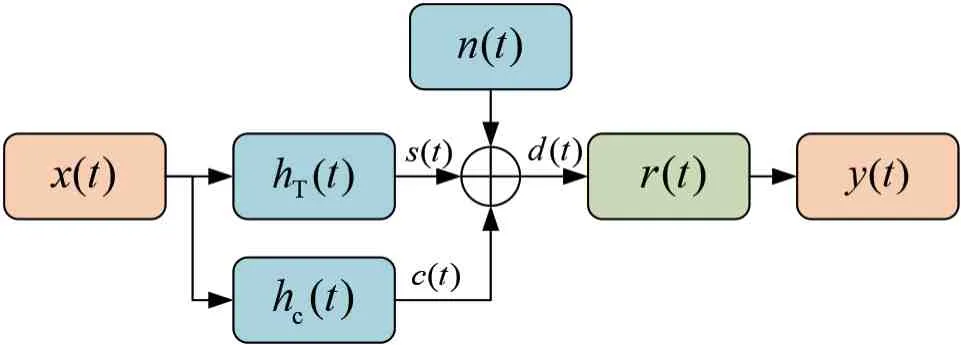
图3 基于SNR准则波形优化的信号模型
图3 中,hT(t)是持续时间有限的目标冲激响应(Target Impulse Response,TIR),在已知目标模型的假设下,其频域能量分布可看作瞬时频率响应幅值的平方,即|H(f)|2;而在随机目标模型的假设下,通常使用能量谱密度(Energy Spectral Density,ESD)来描述能量信号的频域能量分布,即σ2H(f).x(t)表示持续时间有限、信号能量有限的基带发射波形,对应的频域响应为X(f);r(t)为接收滤波器的冲激响应,对应的频域响应为R(f);n(t)是零均值的测量噪声,其PSD 用Snn(f)表示;hc(t)是与信号相关的干扰的冲激响应,其PSD 用Scc(f)表示. 应用柯西-施瓦兹不等式(Cauchy-Schwarz Inequality)得到上述模型导出的信(杂)噪比上界,可以表示为

其中,γSCNR(f)可以看作SCNR 的频域分布,ΞH(f)为目标冲激响应的频域能量分布,

纠博[36]对确知目标联合发射与接收波形的离散形式进行了详细的推导,提出了一种在恒模约束下的相位调制宽带波形优化方法,并利用GA 进行搜索求解.对于确知目标的接收滤波器最优频域响应,可以通过取上述不等式的边界条件获得,即
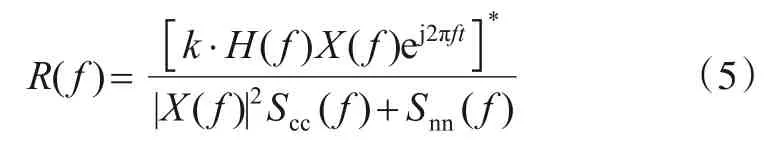
其中,[∙]*表示共轭操作,k表示不为零的常数项.
但是,对于随机目标,Romero[35]并没有给出接收滤波器的严格数学推导过程,SCNR 表达式也仅从直观上将确知目标的频域能量分布替换为随机目标的频域能量分布. 并且,上述算法十分依赖目标、杂波和噪声分布精确已知的假设,不准确的分布信息会导致系统检测性能的恶化.Chen[37]推导了随机目标发射波形和接收滤波器的联合设计算法,首次给出了随机目标接收滤波器的封闭求解方式,并通过引入先验知识辅助,提出单调递增SINR 的迭代联合发射波形与接收滤波优化方法,提高了TIR未知情况下的算法稳健性.
对于运动目标检测(Moving Target Detection,MTD)问题,即目标与雷达之间存在相对运动时,需要进一步考虑匹配滤波多普勒失配的影响,Naghsh[38]和Aubry[39]提出了联合设计发射波形和多普勒滤波器组的方案,增强了动目标检测的性能和稳健性.Karbasi[40]在相似性约束条件下引入了空域信息,提出空时发射编码和空时接收滤波联合优化方法,提高了杂波知识不确定情况下的动目标检测能力.Aubry[41]还考虑了存在距离模糊的运动目标检测,将Stoica[42]建立的回波模型从快时间扩展至慢时间,推导了相应的慢时间波形模糊函数,得到局部模糊函数波形优化方案,但是该方法对包含强杂波的场景信噪比增益有限.
发射波形的恒模约束会带来至少两方面好处:一是使发射功率最大化,二是避免引入对系统性能可能产生负增益的幅度调制. 除频率调制信号外,相位编码信号也是一类常用的具有恒模特性的脉冲压缩序列.Wei[43]在不考虑干扰的确知目标场景下,推导了码片相位矢量关于SNR 的梯度和Hessian 矩阵以及相应的接收滤波器,并逐个优化码片相位. 针对初值敏感的问题,在SNR 有界的情况下,Wei[43]利用目标自相关矩阵最大特征值对应的特征向量作为搜索起点,以尽可能避免算法收敛到局部最优解. 基于SNR 准则的最优波形ESD 与相位编码波形通常没有直接的映射关系,因此必须通过对波形的码片相位进行搜索寻优,使得相位编码波形的ESD 逼近最优波形ESD,Gong[44]在有杂波干扰的条件下,将最小化相位编码波形ESD 与最优波形ESD 的均方误差作为目标函数,根据误差梯度迭代求解发射波形的码片相位序列,得到逼近最优波形ESD 的非量化相位编码波形. 在进一步给定可接受的接收滤波SNR 损失范围条件下,Xu[45]将相位编码波形和失配滤波器进行联合设计,有效减弱了波形-滤波器的互模糊函数(Cross Ambiguity Function,CAF)距离旁瓣对弱目标的遮挡影响.
时域、频域、相位编码域之外,还有一类基于时频变换的波形优化方法. 考虑图4 中的情形,目标与杂波的分布仅从时域或频域上看,均存在不可分离的重叠部分,经典的波形优化方法往往为了抑制杂波,将波形能量集中在目标和杂波分布不重叠或者SCNR 较大的部分,使得目标和杂波重叠部分的信息也被抑制. 但是,从时频域角度分析,在旋转角度α=pπ/2,即阶数为p的分数域u上,目标和杂波的分布则是可分离的.Zhang[46]引入了分数阶傅里叶变换,通过搜索具有特定旋转角的分数域实现目标和杂波的分离. 在Romero[35]的基础上,Zhang 进一步推导了确知扩展目标和随机扩展目标在SCNR 准则下的分数阶傅里叶域波形优化算法. 在图3 信号模型的条件下,仅需将式(3)中对信号求解的传统傅里叶变换替换为具有特定旋转角α的分数阶傅里叶变换,即

其中,Kα(t,u)为旋转角α对应的核函数.
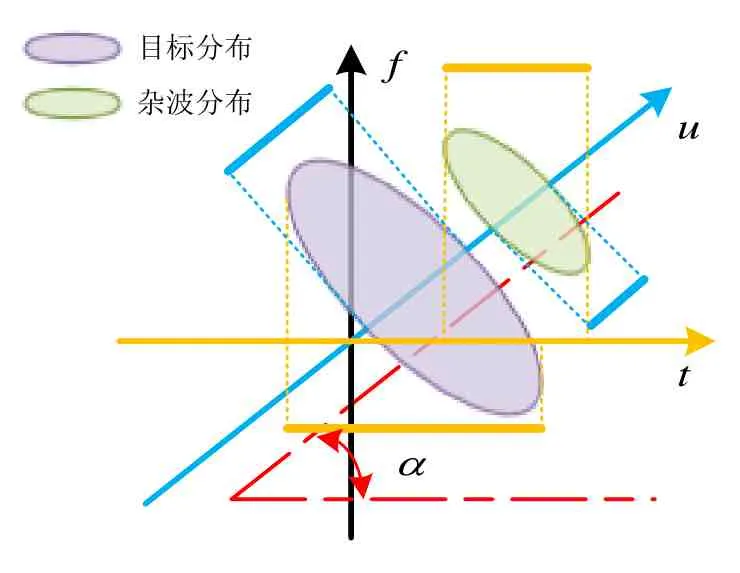
图4 目标与杂波在分数阶傅里叶域内的分布示例
对于其他雷达体制,Zhu[47]针对合成孔径雷达(Synthetic Aperture Radar,SAR)图像目标检测问题以最大化SINR 为目标,对雷达发射波形和距离-方位匹配滤波器进行了联合设计. 在多基地雷达目标检测场景中,Rossetti[48]以正交编码波形为设计对象,在考虑杂波环境的条件下联合发射波形与接收滤波优化,并在后续研究[49]中将该方案应用到认知组网雷达中. Zhu[50]设计了面向MIMO 雷达的鲁棒联合发射波形与接收滤波优化问题. 此外,极化雷达的稳健联合发射波形与接收滤波优化[51]也能够提升雷达在强杂波下的目标检测能力.
(2)基于NP检测器的发射波形优化
在Neymen-Pearson 准则下,最优接收滤波器可以通过发射信号的功率谱推导获得. 因此,检测波形优化的另一个重要研究方向是基于Neymen-Pearson 检测器的发射波形优化,其基本思想可概述为:在给定虚警概率的条件下,目标检测概率可以通过雷达波形的调整得到改善. 作为该方向的奠基工作,Kay[29]引入变分分析法,以有限信号能量和有限信号带宽为约束,在杂波与噪声的PSD 已知的假设下,推导了发射波形的最优PSD. 并在能量约束下提出了高斯杂波中高斯点目标的最优检测波形优化方法[22],首次将通信理论中的“注水法”应用到基于SNR 准则的检测波形优化问题中. 然而,获取目标、杂波、甚至噪声精确的PSD 描述是十分困难的,这也是该类算法在实际应用中受到限制的原因之一.
在宽带雷达应用中,目标会在距离方向上发生扩展,占据多个距离单元,形成距离扩展目标(Range Ex‑tended Target,RET)或者距离分布式目标(Range Dis‑tributed Target,RDT),常用忽略多次散射的一阶Born散射点模型对目标散射特性进行近似建模.Romero[35]将Kay[22]的工作应用到扩展目标检测中,然而使用有限信号带宽约束会导致合成的时域波形具有无限时长而无法实用. Garren[52]首次将匹配照射理论引入目标检测波形优化问题.Deng[53]推导了波形参数与扩展目标检测概率的函数关系,指出一般扩展目标的最优波形是难以求解的,但目标满足刚体或秩1 假设时,其最优波形是存在解析解的,且最大化检测概率与最大化SINR在扩展目标检测波形优化问题中的等价性也得到证明. 在目标和杂波先验未知或者先验不精确的情况下,算法的性能会出现不同程度的恶化.Tang[54]进一步考虑了在目标冲激响应和杂波协方差矩阵先验不确定时,使最差情况下信号SINR 最大化的波形优化问题,实验结果证明了对杂波协方差的对角加载操作能够有效提高算法的稳健性.Sen[55]利用离散傅里叶变换的向量形式wk,将γSCNR(f)中的波形频域表示替换为时域表示,并结合检测概率的表达式推导了偏转系数d2(x)与发射波形x的函数关系:式(7)中各符号含义与式(3)相同. 这种表示方法可以直接对波形的时域形式进行求解,由于Sen 仅考虑了恒模约束,没有对波形相位作出进一步限制,因此上述方案也可以认为是对恒模波形的通用解. 此外,为了使恒模波形保持良好的自相关特性,他将信噪比与自相关函数性能同时作为目标函数,但这2 个准则在本质上是存在矛盾的,只能通过加权的方式在二者之间进行折衷,以获得具有良好自相关特性的次优检测波形. 随后,Sen[56]将上述方法应用于多载频相位编码(Multi-Carrier Phase-Coded,MCPC)波形优化问题中,并与Yin[57]提出的基于离散长椭球序列(Discrete Prolate Spheroidal Sequences,DPSS)的波形优化方法进行对比. 仿真结果表明,在检测性能相当的情况下,基于MCPC 的方法具有更低的计算复杂度. Yao[58]提出了一种以扩展二进制相移键控(Extended Binary Phase-Shift Keying,EBPSK)波形为设计对象的稳健波形优化方法,可以缓解未知目标多普勒频移引起的检测性能下降.
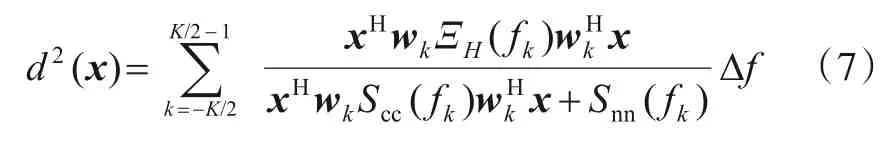
除上述对单脉冲码片相位进行设计的脉内调制外,还有一类考虑脉间调制的相参脉冲串编码波形优化方法,该方法的奠基工作和信号模型主要由De Maio[59~63]建立,该模型可以表述为
r=αc⊙p+w(8)
其中,α是接收滤波器输出的复幅度参数,综合考虑了发射波形的幅度、相位、载波频率以及目标时延、反射率和信道传播效应等;c是各脉冲的相位编码序列;p是时间导向矢量;w是系统测量噪声;⊙表示矩阵的Had‑amard 乘积. 在上述模型的基础上,分别推导了起伏模型和非起伏模型的检测概率[59]:

其中,Q(∙,∙)为一阶Marcum Q 函数;γSNR为回波的SNR,相应的表达式为
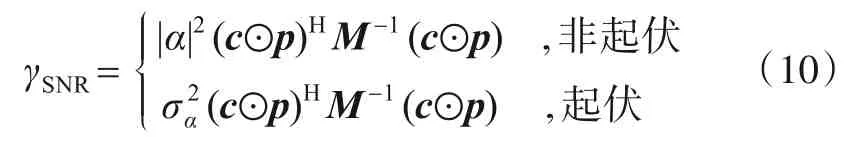
其中,M=E[wwH]为噪声协方差,E[∙]是统计期望计算符号.De Maio 同时考虑了运动目标多普勒测量的精度与波形之间的关系,通过给定多普勒估计精度下界δα,可以得到
(c⊙p⊙u)HM-1(c⊙p⊙u)≥δα(11)
可以看出,最大化SNR 和多普勒估计精度是存在冲突的,为了得到优化解,De Maio 将上述优化问题构造为一个非凸齐次二次约束二次规划问题[59],并对最差情况下的SNR 进行优化,给出了稳健的非量化相位编码波形[60]、量化相位编码波形[61]以及峰均功率比(Peak to Average Power Ratio,PAPR)约束下[62]的设计方案;此外,他还通过引入标量化方法,将上述优化问题构造为一个帕累托优化问题[63],推导了帕累托权重对目标检测性能的影响. 针对上述方案中可能存在非确定性多项式时间难题(Non-deterministic Polynomialtime hard,NP-hard),Soltanalian[64]利用半定松弛(Semi-Definite Relaxation,SDR)和二次优化的方法推导了相应的次优解.
3.1.2 基于信息论的检测波形优化
仅对于检测任务而言,最大化SNR 的确能够有效提高目标的检测概率,但Woodward[65]也指出,目前仍没有理论表明最大化SNR 能够保证获取最多目标信息. 1993 年,Bell[66]将信息论应用在雷达波形优化中,首次在检测任务中引入了雷达通道模型并提出了基于互信息(Mutual Information,MI)准则的波形优化思想,将得到的最优波形称为“信息提取波形”或“估计波形”. 目前,以信息论为基础的波形优化研究工作大致上可以分为2 类:一类是基于互信息准则研究雷达体制、约束条件、目标和环境模型的波形优化方法;另一类是通过信息论建立起不同评价指标之间的关系.
(1)基于互信息准则的检测波形优化
贝叶斯观点认为,概率密度函数封装了关于随机变量的全部知识,即可以通过某种算子在概率密度上得到所需的目标信息. 随机向量x和z的互信息通常可以由下式定义:
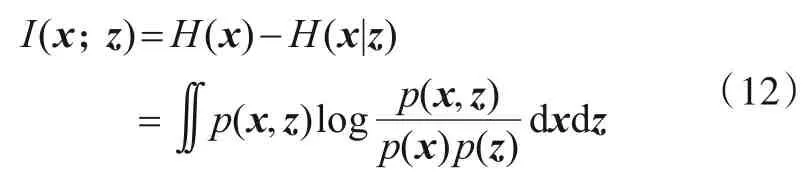
其中,H(∙)为香农熵,其大小表示随机变量的不确定性;p(,)表示随机向量的概率密度函数;x表示感兴趣的目标状态;而z是对x的某种测量,则互信息表示获得测量数据z后,目标状态x不确定性的减小量. 利用Kull‑back-Liebler 散度(Kullback-Liebler Divergence,KLD),互信息可重写为
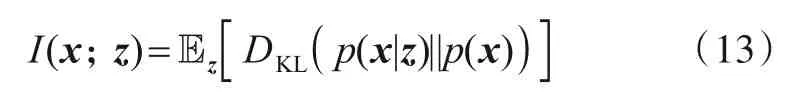
其中,DKL(pB(∙)||pA(∙))表示概率密度pA(∙)与概率密度pB(∙)的KL 散度. 目标状态x与测量数据z的互信息等于目标状态x的后验概率密度p(x|z)与先验概率密度p(x)之间KL散度的期望,即后验概率密度p(x|z)与先验概率密度p(x)的平均差异越大,则测量数据z包含的目标信息越多. 王建涛[13]指出,基于SNR 准则和基于信息论准则得到的最优波形具有明显的差异,如图5 所示,使用最大化互信息准则得到的波形回波中携带了目标的更多信息.
以Bell的工作为基础,基于信息论的研究通常利用目标冲激响应(Target Impulse Response,TIR)与雷达接收回波之间的互信息作为代价函数进行波形优化. 利用图3模型,可以推导信号的互信息:
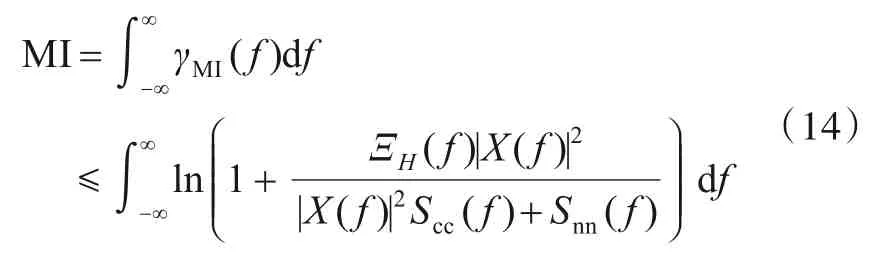
对比式(3),则SCNR 频域表示与MI 频域表示的关系为
γMI(f)=ln(1+γSCNR(f)) (15)
在能量约束条件下以互信息为目标函数的波形优化问题,通常可使用拉格朗日乘数法,将问题转为求解最优波形能量谱密度的凸优化问题,相应的方法同样被称为注水法. 纠[67]进一步考虑杂波的影响,提出了通用注水法. 如图5 所示,与基于SNR 准则的最优波形将能量集中于SNR 最大的窄带频点处不同,基于MI 准则的最优波形倾向于使能量分布在目标频谱对应的频段上,这是由于式(15)中的对数运算降低了各个频率成分的系数差异.

图5 基于信噪比与互信息准则的最优波形示意图
PAPR 约束会导致优化问题的非凸性.Hao[68]利用MM 算法和Toeplitz 矩阵性质,将非凸问题转化为关于求解向量变量的凸优化.Wang[69]把多目标分类问题建模为多假设检验过程,利用KL 散度描述不同假设概率密度函数间的距离,并引入SDR和半定规划(Semi-Defi‑nite Programming,SDP)技术来解决非凸的波形优化问题,但算法的计算量随目标数的增加而增大,并且没有考虑杂波对信号的影响.
针对MIMO 雷达,De Maio[70]对比了下切诺夫界作准则和MI 准则优化得到的波形性能,指出由这2 种设计指标推导出的最优波形具有相同空时编码矩阵,并且与目标几何结构和干扰子空间之间具有简洁的函数关系.Tang[71]利用相对熵作为优化准则,在恒模和相似性约束下,使用MM 算法将MIMO 检测波形优化转化为二次优化问题,并且引入了平方迭代法(squared itera‑tive method)提高算法收敛效率.Sun[72]通过上界松弛和MM 算法将波形设计分解为两阶段优化问题,利用交替方向乘子法(Alternation Direction Method of Multipliers,ADMM)推导了发射波形的最优解,有效增强了MIMO雷达的空时自适应处理(Space-Time Adaptive Process‑ing,STAP)检测能力.Chen[73]在设计分布式MIMO 雷达波形时,同样提出了一种两阶段的优化方案,在第一步中最大化目标冲激响应与接收回波之间的MI,然后在第二步中最小化目标冲激响应之间的互信息来提高多目标检测和特征提取的性能.
此外,优化OFDM 波形用于提升扩展目标认知检测性能[74]和给定目标功率谱上下确界的先验知识以提高波形优化算法稳健性[75]也在相关工作中得到了验证.
(2)基于信息论的评价指标关联
基于信息论波形优化的另一个重要研究方向是通过信息论建立起不同设计准则之间的关系.Romero[35]推导了波形优化中SNR 和MI 准则之间的关系,针对不同环境模型给出了相应确知目标和随机目标的波形优化方法. 在描述随机目标冲激响应模型时,他指出[76]使用功率谱密度(Power Spectral Density,PSD)表征持续时间有限的随机目标是不合理的,需要引入能量谱方差(Energy Spectral Variance,ESV)或功率谱方差(Power Spectral Variance,PSV)来描述随机目标的统计特性.Zhu[77]提出一种色噪声环境下基于KLD 的扩展目标检测波形优化方法,推导了在该问题中的3 个设计指标(SNR,MI,KLD)之间的关系. Xiao[78]将SNR 作为优化约束,对比了基于MI 和基于KLD 准则波形的差异,进一步推导了KLD 与J 散度(Jenson-Shannon divergence)的关系. Li[79]利用拉格朗日乘数法验证了MIMO 体制中将J散度作为波形优化准则的可行性.
3.1.3 基于机器学习的检测波形优化
Haykin[3]在提出认知雷达概念时,将认知发射建模为马尔科夫决策过程. 他认为认知雷达是一种“部分可观测”的随机控制系统,求解这类系统控制决策问题的最优解通常是NP 难问题. 因此他指出利用强化学习(Reinforcement Learning,RL)、Q 学习(Q-Learning,QL)等次优方法在系统可接受范围内可以提出一些解决方案. 近年来,随着计算机算力的增加和训练数据获取难度的降低,机器学习算法在许多领域都展现了惊人的性能,一些研究工作也将相关的算法应用于雷达探测领域.
MIMO 雷达可通过设计发射波形来实现显著的相参增益从而提高检测性能,同时发射信号的波束形状也可以抑制某些方向上的干扰使得期望方向上的增益最大化[80]. 针对上述特点,Ahmed[81]和Wang[82]利用强化学习,在目标数已知及没有干扰的条件下,仅根据当前时刻所获得的信息对波束进行合成,从波形空间分集的角度改善了未知环境中雷达目标的检测性能,避免传统方法中需要先计算波形协方差矩阵,再根据矩阵进行波束形成的步骤.Jiang[83]将一个利用监督学习训练的检测器和一个利用强化学习训练的发射器进行串联,设计了一种端对端的联合发射波形和接收滤波优化方案. 但是奖励(reward)的设置不合理可能导致算法不能正常工作甚至完全失效,并且即使给定合理的奖励函数,模型学习得到的策略并不总是稳健的.Thornton[84]在频谱拥挤环境下,基于深度Q 网络(Deep Q Network,DQN)制定了认知雷达最优探测与频谱共享策略,其基本思想是通过调整线性调频(Linear Fre‑quency Modulation,LFM)波形的带宽和中心频率,降低其他系统的干扰,并且还引入了双网络结构以克服DQN 训练过程中的过估计问题,提高目标检测性能的同时充分利用可用频带来实现良好的距离分辨率. 循环神经网络(Recurrent Neural Network,RNN)是另一类能够描述系统动态行为的机器学习算法,能够比较好地解决时间数据序列长期依赖的问题.Baptiste[85]提出一种能够在有限解空间中,利用长短期记忆网络(Long Short-Term Memory,LSTM)快速实现自编码和干扰陷波的波形优化方法.
3.2 面向跟踪任务的波形优化
在雷达应用中,基于贝叶斯框架的目标跟踪可以等效为一个利用先验知识和观测数据对目标参数进行动态估计的问题. 贝叶斯跟踪滤波是一类模型驱动的迭代算法,每个迭代过程一般包含预测和更新2 个步骤,分别由目标动态模型和传感器观测模型描述. 对于不同类型、不同体制的雷达传感器,观测模型的具体形式也不尽相同. 在一定条件下,过程噪声和观测噪声对跟踪性能的影响是相互独立的[86],雷达跟踪性能与测量数据特性紧密联系,而测量数据特性与波形有关. 因此,大多数面向跟踪任务的波形优化是以提高目标和环境的观测质量为目的. 这其中必然涉及波形与量测之间的关系如何定量表示的问题. 早在20 世纪70 年代,Fitzgerald[87]就针对测距雷达LFM 波形与跟踪精度的关系进行了详细研究,并指出由于距离多普勒耦合系数符号不同,雷达发射正调频率的LFM 信号会得到较高的跟踪精度,但并没有进一步指出如何选择优化波形.
Haykin 教授在2009 年正式提出认知跟踪雷达(Cognitive Tracking Radar,CTR)概念[88],他指出CTR 的认知特性不仅体现在发射机和接收机的闭环反馈结构,也体现在系统与目标环境之间的全局“感知-动作循环”(Perception-Action Cycle,PAC). 同时,他提出了一种基于波形选择的认知跟踪实现框架[89],在该框架下,接收端采用容积卡尔曼滤波器(Cubature Kalman Filter,CKF)对目标状态进行预测估计,以改善忽略高阶项的贝叶斯滤波低阶近似引入的误差;而发射端则将最优发射波形选择问题转化为随机动态规划问题,采用QLearning 算法克服目标状态转移概率先验未知,并建立目标状态与相应最大检测概率波形的关系,得到仅次于动态规划的次优解.Haykin[90]和Smith[91]分别通过计算机仿真和实验验证了CTR 的可行性,证明了CTR 相比于传统开环结构的雷达,能够显著提高目标跟踪性能. Bell[92]在Haykin 的基础上提出了一种可用于资源调度的认知雷达跟踪框架.
目前,目标跟踪性能与波形参数之间主要通过2种方式建立联系:观测数据质量和信息论.
3.2.1 基于观测数据质量的跟踪波形优化
模糊函数(Ambiguity Function,AF)是雷达波形分析与优化的常用工具,刻画了无噪声干扰条件下,波形与对应的匹配滤波器的特征和性能,可以用于分析给定波形的分辨率、旁瓣特性、距离多普勒测量性能.1994 年,David[93]利用卡尔曼滤波对最优跟踪波形优化问题进行研究,提出了跟踪波形的2个常用优化目标函数:最小化均方跟踪误差和最小化相关波门体积.他将雷达波形模糊函数在原点处的Fisher 信息矩阵建模为雷达测量数据误差协方差的克拉美罗下界(Cram‑er-Rao Lower Bound,CRLB),以表征测量与波形参数之间的关系. 随后将存在信号相关的杂波情况纳入到算法中,给出了基于概率数据关联(Probabilistic Data As‑sociation,PDA)的单目标跟踪最优波形优化方案[94]. 然而对于矩形脉冲波形,对应的时延、多普勒估计的Fish‑er 信息矩阵没有解析表达式,其模糊函数在原点处不可导. 为此,Sira[95]利用梯形包络替代矩形包络,以更好地满足方法在实际应用中的可行性. 尽管Grishin[96]在其研究中指出,面向跟踪任务的最优波形优化对系统的SNR 并不敏感,但CRLB 和Fisher 信息矩阵通常只用于SNR 较高的情形,在低SNR 时,一般优先考虑使用先验界.
此外,上述算法的问题还包括[13]:(1)仅考虑波形模糊函数在原点处的形状而忽略了旁瓣的影响;(2)实际雷达测量精度与参数估计CRLB 之间是不等价的,并不能准确反映雷达测量数据的统计特性;(3)雷达测量误差协方差只能部分描述雷达测量数据与波形之间的关系,雷达发射波形还可能影响雷达回波中包含的目标信息量、SNR和检测概率等.
对于第一个问题,加窗函数操作是最直观的降低旁瓣的操作之一,不同的窗函数具有不同的性质,但是总体而言,加窗函数操作减小旁瓣都是以降低主瓣分辨率作为代价的. 通过波形的调制也是一种降低旁瓣的手段,如非线性调频信号和相位编码信号都具有图钉状的理想模糊函数,这类模糊函数能够提供优秀的参数估计性能,但通常具有差的多普勒容忍性,当目标的多普勒频移较大时,会产生系统性能损失.Benedet‑to[97]详细分析了一类具有恒模零自相关(Constant Am‑plitude Zero Auto Correlation,CAZAC)特性的编码序列用作发射波形时雷达的探测性能.
对于第二个问题,由于跟踪算法的观测数据来源于检测和估计过程,Rago[98]提出一种面向跟踪任务的条件平均混合恒频和扫频联合波形的系统,引入了距离和多普勒分辨单元的概念,对检测概率、虚警概率等检测任务使用的评价标准和观测数据的质量之间的关系进行了深入的研究.Niu[99]对分辨单元理论进一步完善,并研究了不同波形对跟踪性能和精度的影响.Sav‑age[100]在机动目标应用背景下,证明了距离、距离率测量的负相关系数能够提高跟踪精度. 但是,上述工作是对雷达发射不同波形的稳态跟踪精度进行分析,并没有研究动态波形自适应. 王璐璐[101]指出由波形模糊函数给出的名义分辨率(Nominal Resolution,NR)仅代表了波形固有的分辨能力,并引入了统计流形,提出一种基于KLD 的实际分辨率度量方法,通过最大化实际分辨率对波形进行综合设计,解决了雷达实际测量数据的统计特性的表征问题.
对于第三个问题,Gelfand[102]最早考虑了检测门限对跟踪系统性能和发射波形的影响. 在SNR足够大时,Hong[103]给出了平均检测概率的近似表达式,并推导出在高SNR 条件下高斯包络LFM 脉冲的误差协方差阵近似表达式. Wang[104]将修正的Riccati 方程用于预测包含波形参数和检测概率的量测误差协方差,并作为准则函数对发射波形和检测概率进行联合优化. 杨[105]则引入了压缩感知(Compressed Sensing,CS)理论,通过构建观测模型的稀疏表示,推导后验克拉美罗界(Posteri‑or Cramer-Rao Bound,PCRB)与发射波形参数的函数.上述算法没有全面考虑观测数据可能同时存在漏检、野值等问题,在特殊情形下对算法的稳健性具有较大的挑战性.
针对扩展目标跟踪问题,Dai[106]利用宽带目标冲激响应在慢时间上存在相关性的特点,建立目标响应的统计递推模型,以其为状态参数建立对应的状态方程和测量方程,通过线性卡尔曼滤波器在最小均方误差(Minimum Mean Square Error,MMSE)的准则下[107],使得目标冲激响应的估计误差最小,从而利用得到的TIR估计调整发射波形的参数. 在恒模约束下,该问题为一个非凸的二次规划问题,同时由于目标冲激响应在慢时间上是广义平稳,而在快时间(距离维)上是不平稳的,因此相应的频域功率谱也是不存在的.Dai[108]通过将问题转化为利用波形减小观测误差求解次优频谱,通过相位驻点法和迭代最小二乘法得到时域的相位编码波形.
可以看出,上述基于观测数据质量的跟踪波形优化方法,是推导波形参数与量测数据之间的关系,通过提高观测质量从而间接提高跟踪结果的精度,并没有真正与跟踪的滤波过程相结合.
3.2.2 基于信息论准则的跟踪波形优化
Sira[109]将认知跟踪波形优化分为两大类方法,一类是基于控制理论的跟踪波形优化方法,另一类是基于信息论的跟踪波形优化方法. 其中,基于信息论的跟踪波形优化方法通常使用的是最大化目标观测和目标状态之间的互信息:

其中,I(xk;z1:k)是观测数据z1:k和目标状态xk的互信息,θk是波形参数.
2007 年,Savage[100]讨论了LFM 信号的调频率与目标机动指数的关系,指出最优调频率可以使观测误差椭圆与预测误差椭圆相互正交,正式提出了误差椭圆正交的概念. 误差椭圆是利用图形化的方法,描述随机变量概率密度分布的二阶矩,当一个服从高斯分布的随机变量,其无偏估计的精度由协方差决定,如图6 所示. 这种椭圆误差法也被认为是基于最大化互信息准则的波形优化所对应的物理意义解释,Sira[109]利用观测协方差的CRLB 与预测协方差从数学上定量地描述了发射波形参数与观测协方差CRLB的关系.

图6 误差椭圆概念图形化表示
在贝叶斯跟踪框架中,目标状态的估计误差由目标运动误差椭圆(球)和测量误差椭圆(球)相交的区域大小决定,当2 个误差椭圆(球)相互正交时,重叠区域的面积达到最小,这种误差椭圆(球)正交法下,最小均方误差准则和最大互信息准则是等价的[110].Rago[98]和Savage[100]分别基于多项式预测模型和标准交互多模型(Interacting Multiple Model,IMM),利用分数阶傅里叶变换(Fractional Fourier Transform,FrFT)来旋转模糊函数,从而完成观测误差椭圆的旋转,然而由FrFT分数域得到的频谱综合得到的时域波形会引入幅度调制.檀[111]给出了误差椭圆正交理论的相关数学推导,证明了在线性高斯噪声背景下,基于卡尔曼滤波的最大化目标预测状态与观测值之间的互信息与最小化感知信息熵(即最小化后验估计误差协方差矩阵的行列式)是等价的.Jin[112]给出了LFM波形和旋转波形参数在最大化互信息准则下的目标函数表达式. Suvorova[113]在Savage[100]工作的基础上,预先建立波形库以降低目标跟踪和波形优化过程的复杂性.Turlapaty[114]将最小化自由能(Free Energy,FE)原则引入跟踪波形优化中,使得参数估计与波形优化能够统一到一个框架下,证明了在单个未知参数的情况下,基于FE 的估计量与贝叶斯估计量是相同的,且得到的优化波形与基于MI 得到的注水波形相似.Leshem[115]将注水法推广到多目标场景,根据不同目标的优先级,利用线性加权多目标TIR和回波之间互信息的方法,给出了在联合功率约束条件下的波形优化方法.
跟踪波形优化问题通常还需要结合具体的应用场景或波形类型进行分析. 针对存在多径干扰的场景,Chavali[116]以后验CRLB 为优化准则,对OFDM 信号子载频系数进行优化以满足跟踪性能需求.Godrich[117]将最小化跟踪贝叶斯克拉美罗下界(Bayesian Cramer-Rao Lower Bound,BCRLB)作为目标函数,对分布式雷达目标跟踪问题的资源调度和波形空间分集进行规划,求解最优发射参数.Kyriakides[118]考虑了多目标跟踪的波形优化问题,但是仅等效为单目标跟踪的简单叠加或只考虑分辨率的影响,并没有对多目标跟踪中的数据关联问题进行研究. 对于先验知识不准确或者缺失时的算法稳健性下降风险,Zhong[119]提出了一种基于自适应无迹卡尔曼滤波器(Adaptive Unscented Kalman Fil‑ter,AUKF)的鲁棒认知雷达跟踪方法,额外引入了噪声协方差的估计模块以保证算法的稳健性.Feng[120]提出了一种结合矩阵加权多目标模型与观测融合的波形优化方法,提高认知雷达对机动目标的跟踪稳健性,克服了观测野值的问题.
机器学习算法在跟踪波形优化中的研究仍处于起步阶段,大体上只是将不同模型和算法应用在CTR 框架上,如深度RL[121],DQN 等. 总的来说,面向跟踪任务的波形优化的本质目的都是为了减少后验估计误差,从图6 可以看出,上述2 类方法的区别在于:基于观测数据质量侧重于减小测量误差椭圆的自身大小,即提升测量精度;而基于信息论则侧重于通过旋转测量椭圆,使预测误差椭圆和测量误差椭圆的交集最小,即提高测量中目标的信息量.
3.3 面向成像任务的波形优化
雷达成像技术是利用不同视角下目标散射点间存在的多普勒差异,经过一定算法的处理获得的目标散射特性图像,是雷达从简单的搜索跟踪测量阶段迈向目标特征测量阶段的重要技术. 通过一维距离成像、(逆)合成孔径雷达成像、微多普勒时频图像,可以获取目标的外形、体积、表面物理参数、微动参数等,为后续分类识别任务提供目标的特征. 不同的雷达波形会影响成像效果,例如具有图钉状模糊函数的波形通常会产生良好的成像结果,目标的主要散射点可以有效地被凸显出来,且不会遮挡其他弱散射点.
2009 年,Cheney[122]指出波形优化与反馈优化对SAR 成像系统性能的提升和改善产生显著影响. 基于散射中心理论,目标一般满足稀疏性要求,Yoon[123]与Zhang[124]在Haykin 提出的认知雷达框架上,结合压缩感知理论,进一步讨论了波形参数与逆合成孔径雷达(Inverse Synthetic Aperture Radar,ISAR)成像之间的关系. 上海交通大学雷达信号处理实验室在2012 年也提出了“认知成像”的相关概念[125,126].
除信号模糊函数外,常用的成像优化准则还包括重构的与真实目标散射函数间的最小距离、模糊函数最优和克拉美罗限等. 现有面向成像任务的波形优化工作大致上也可以分为脉间波形优化和脉内波形优化2个研究方向. 脉内波形优化与面向其他任务的波形优化方法类似,主要思想是在如能量、恒模等约束条件下,通过求解由系统性能指标表征的目标函数,得到满足需求的波形参数,这类方法通常以获得目标高分辨距离像(High Resolution Range Profile,HRRP)为目的进行设计的;而脉间波形优化则更多考虑目标的二维像,即SAR 成像和ISAR 成像,由于目标散射的时变特性,成像前需要对不同脉冲进行补偿处理,通过优化波形降低目标像重构难度,进而实现完整的认知成像流程.本节分别从HRRP,ISAR和SAR成像波形优化3个方面进行梳理.
3.3.1 HRRP成像波形优化
为了获得高的距离分辨率,雷达成像常用的波形以宽带信号为主. 陈[127]通过将波形优化转化为概率分布的互相关参数及其协方差矩阵条件数的寻优问题,联合设计步进频率信号脉冲重复时间间隔序列和子脉冲频率序列,不仅能够实现目标一维距离像的高概率重构,还能同时优化信号模糊函数.Gu[128]以具有高斯混合包络的扩展目标为对象,提出一种基于互信息的频域波形优化方法以得到更加准确的目标一维距离像,然而这种近似忽略了波形旁瓣的影响. 基于交替投影思想,Li[129]提出了一种可用于设计具有低自相关旁瓣离线波形库的迭代频谱近似法.
考虑目标距离像散射中心的稀疏特性,He[130]提出利用约束等距常数(Restricted Isometry Constant,RIC)作为优化问题的目标函数,通过对多相编码信号进行优化,在SNR 较低的条件下实现压缩感知雷达的稀疏重构成像. 而对于目标频率响应的稀疏性,龚[131,132]提出一种动态调整信号带宽的MIMO雷达波形优化方法,根据目标的一维距离像自适应设计能够分辨多个不同目标距离散射点所需的最小发射信号带宽,能够在完成多目标成像的同时节省雷达带宽资源.
3.3.2 ISAR成像波形优化
对于ISAR 成像,目前大部分认知发射技术的研究工作主要集中于通过波形优化提高目标运动补偿的精度或者降低运动补偿的复杂度. 另外,通过压缩感知等技术提高一维距离像的重构精度,从而间接提高ISAR图像成像质量的研究工作也被归入本节进行讨论.
Hu[133]将现有的循环算法(Cycle Algorithm,CA)通过稀疏恢复(Sparse Recovery,SR)进行改进,利用对目标结构的认知调整发射波形,改善MIMO雷达非正交波形成像结果质量不佳的问题. Zhang[134]提出一种基于稀疏步进频信号的ISAR 成像波形优化框架,通过精确的运动补偿和横向相参积分,提高重构距离像的稀疏度和SNR,从而提升了ISAR 成像的稳健性.Zhou[135]进一步考虑稀疏步进调频波形,通过回归算法实现目标径向运动残差的精确估计,得到高质量的HRRP,并以图像熵为目标函数,利用遗传算法迭代优化,以获得具有良好聚焦效果的ISAR 图像. Liao[136]针对随机步进频波形的距离-多普勒耦合,提出一种互补编码对消算法,能够完成目标速度的估计并实现精确的运动补偿. 对于高速机动目标,Kang[137]同时考虑了脉间和脉内平动补偿,提出一种基于压缩感知的间隙步进频波形(gapped stepped-frequency waveform)优化方法.Wei[138]推导了信号的步进频率和编码相位与波形模糊函数旁瓣的关系,并基于共轭梯度优化算法,提出了一种二维图像重建技术[139],通过使用频率和脉冲重复频率捷变的脉冲序列,降低了信号的多普勒旁瓣,消除了频率和距离的耦合.
3.3.3 SAR成像波形优化
尽管“认知成像”概念是近几年才正式提出的,但是T. Varslot 在2007 年的研究中就提到了面向成像的波形优化,他引入了变分法,通过最小化TIR 与重建图像之间的均方误差对认知SAR 的波形优化进行了探索[140].
Wang[141,142]提出一种利用杂波和目标特性离线设计波形库,进行成像处理时再对目标和场景与波形库进行匹配,初步实现了具有动态调整的认知功能.Zhu研究了基于认知SAR 的波形优化和闭环反馈的问题,针对杂波抑制问题和多目标问题,分别提出了具有杂波抑制能力的认知SAR 系统结构[143],以及多目标场景面向SAR 成像任务的波形优化方法[144].2017 年,Aber‑man[145]针对认知SAR 开展了自适应频率分集方法研究,提出了LFM 信号的几种下采样方案,并证明不限制动态变化的随机采样更适合SAR系统.
认知成像波形优化与不同成像体制的应用相结合,如对视频圆周合成孔径雷达(Circular Synthetic Ap‑erture Radar,CSAR),Mitchell[146]提出一种分辨率可变的认知成像框架;Idriss[147]提出一种面向探地雷达的基于匹配照射理论的发射波形优化方法,能够在抑制杂波的同时,提高目标二维成像质量,并利用粒子群优化和Taguchi 优化算法分别给出了快速实现过程,在稀疏分布的多基地雷达场景中[148]也得到应用;Wang[149]将LFM 分集波形应用到MIMO-SAR 系统中,提出了一种能够实现高距离分辨和良好的多普勒容限的发射波形优化方法,不仅能够满足恒模约束,还能满足信号正交性的要求. 此外,包括线性调频连续波[150]和非线性频率调制(Nonlinear Frequency Modulation,NLFM)[151]波形在内的各类宽带波形在认知SAR 的应用可行性也得到了验证.
3.4 面向分类任务的波形优化
目标分类问题,通常是指通过提取目标稳定且有标志性的特征,对不同目标进行划分的过程. 典型的分类方法是通过一维距离像、二维SAR/ISAR 图像或者时频图像提取目标特征实现的. 广义的目标识别(target recognition)可分为目标辨别(target discrimination)、目标分类(target classification)和目标辨识(target identifi‑cation)3 个层次,本节内容对上述概念不再详细区分,相关算法均归类为面向分类任务的波形优化.
对于分类任务,基于SNR 准则或互信息准则的目标函数无法建立与分类性能直接相关的映射关系,如基于互信息的波形可以提高单个目标信息的获取,却无法进一步与其他目标在特征空间上分得更开.Good‑man[152]指出并不存在单一发射波形谱密度能够完全覆盖所有潜在的目标,即使存在也无法分辨所有的目标,因此对于面向分类任务的波形优化技术,必须将波形匹配于特定目标的思想转换为利用波形增加不同目标之间的区别度,如对于2 类目标的分类问题,将2 类目标的冲激响应的差作为目标,通过构建能够使这种差异最大化的代价函数或距离测度,如欧氏距离、马氏距离[153]、最小匹配距离/相关距离[154]和KLIN(Kullback-Leibler Information Number)[155]等.
目前,面向分类任务的波形优化有2类经典的设计思想:一类针对单次观测的基于匹配照射理论的分类波形优化,将目标间特征响应的差异作为系统响应,通过发射与之相匹配的波形以增大该差异;另一类则是针对多次观测,基于序贯假设的分类波形优化,其将分类问题转化为多类别假设检测问题,通过序贯统计量判断目标符合的类别假设.
3.4.1 基于匹配照射理论的分类波形优化
Kennaugh[156]研究发现目标冲激响应中的自然谐振分量与发射波形频率及目标的姿态无关,是理想的识别特征,然而这种特征在实际应用中是难以获得的.因而主流研究都将目标冲激响应中的冲激分量作为研究对象(文中TIR 应均指目标冲激响应中的冲激分量). 1986 年,Gjessing[157]在其著作中讨论了匹配照射理论在目标检测中的应用,随后Pell[158]指出该理论可以用于解决目标识别问题,因为发射与目标匹配的波形能够更好地描述目标的特征,Garren[159]进一步认为匹配照射理论能够将面向目标检测和目标分类任务的波形优化有机地统一起来.Shirman[160]和Jin[161]对信号带宽、载频、SNR 等参数与目标分类性能的关系进行了细致的分析.
Bell[66]从信息论观点出发,认为当目标的先验知识不足时,可以利用一个随机过程来描述目标的冲激响应,如复宽平稳随机过程(Complex Wide-Sense Station‑ary,CWSS). 严格来说,基于最大化MI准则的波形优化方法需要同时满足目标、杂波、干扰、噪声均为高斯随机过程的要求. 但是对于确定性冲激响应的目标分类任务,Goodman[152]认为由于目标类别本身的不确定性使得在一定的约束条件下,仍然满足基于互信息的波形优化方法的假设. 如前所述,面向分类任务的波形优化不能直接以目标冲激响应与接收回波的互信息作为目标函数进行优化. 为了能与分类性能指标相结合,Guerci[162]将2 类目标冲激响应的差异构建为一个新的系统冲激响应,推导该冲激响应在不同条件下的距离测度,如在高斯白噪声条件下表现为欧氏距离,而在色噪声条件下表现为马氏距离,并结合联合发射与接收波形优化技术,使该距离最大化,该方法同样适用于全极化雷达[153]. 当场景目标大于两个时,上述方法需要通过对多个目标冲激响应加权进行推广. 纠[163]认为目标复数距离像存在姿态和平移敏感性,不能直接用于识别,提出了利用识别特征和目标特性间MI 的波形优化方法,并称之为特征互信息法.Kim[164]利用基于能量谱方差的互信息(Mutual Information based on Energy Spectral Variance,MIESV)准则,设计了一种适用于目标分类的波形,并通过Jensen 不等式从数学上严格推导了MIESV下界.
除信息论准则外,Xu[165]利用Pearson 相关系数构建目标函数,综合考虑了目标信息获取能力、分类正确率和空间分辨率,在能量约束下提出基于信息失真概念的波形优化方法.Rui[166]引入了概率加权能量(Prob‑ability Weighted Energy,PWE)波形的设计方法,以增加计算复杂度为代价,提高系统对非高斯目标分类的稳健性.Nieh[167]基于最大后验概率加权特征波形(Max‑imum A Posteriori Probability Weighted Eigenwaveform,MAP-PWE)和匹配滤波特征波形(Match-Filtered Prob‑ability Weighted Eigenwaveform,MF-PWE),提出了一种可以联合距离-多普勒定位与目标分类的波形优化方法.Tan[168]分别基于SNR 和MI 准则提出PWE 与概率加权谱方差(Probability-Weighted Spectral Variance,PWSV)的匹配照射分类波形优化方法,考虑理想散射点模型忽略目标特显点以外重要特征分量的问题,Tan利用电磁仿真目标数据,验证了不同方位角下目标的分类性能.Alshira[169]推导了能量约束下最小化分类错误概率分类波形的解析解,并在非自适应框架下考虑了费雪判别分析,通过使费雪可分性最大化,提高系统的目标分类性能,尽管性能优于包括基于平均马氏距离(Average Mahalanobis Distance,AMD)等的非自适应波形优化方法,但没有进一步指出算法对动态变化环境的适用性. 针对这一问题,Alshira[170]在随后的研究中提出了一种针对频域的自适应波形优化方案,证明了发射波形能量的高低并不能显著改善系统的目标分类性能.
3.4.2 基于序贯假设的分类波形优化
目标分类可以看作在目标检测的基础上,进一步对不同目标假设进行检验的过程. 除了基于匹配照射理论的分类波形优化,还有一类方法利用序贯假设检验的方法,在多次雷达观测后,综合考虑每一类假设情形及对应的分类风险进行最优波形优化,以提高目标分类的性能. Fan[171]将在高斯杂波条件下的目标分类问题转化为均值偏移的高斯-高斯概率分布函数假设检验过程,证明了使分布位移最大的发射波形能够得到更好的目标分类性能. 随后,以各个目标冲激响应与接收信号间的互信息线性加权和(Weighted Linear Sum,WLS)为目标函数,各目标分量的权重与上一时刻的分类概率成反比,通过简化模型实现波形最优化方程的降维,得到目标数目较少时最佳分类波形优化方法[172].
目标高分辨距离像的姿态敏感性会导致TIR 在快时间不存在确定的功率谱密度,然而从慢时间维度看,各次观测之间又存在一定的相关性. 在静止目标假设下,Romero[173]认为可把多次雷达观测数据中的目标冲激响应认为是同一随机过程的多次采样,并提出一种多假设检验(Multiple Hypotheses Testing,MHT)波形优化框架,提高了PWSV 波形优化[168]算法计算效率.Alshirah[174]针对非自适应体制的分类波形优化问题,指出目标在整个角度空间上具有相同统计平均特性的假设会导致目标的粗糙表示和系统性能的退化. 为了克服目标特征的姿态敏感性和时间相关性,Wu[175]引入了静态多模型和指数衰减模型来描述目标特征的动态变化,利用互信息对所有目标假设的平均估计能力和假设之间的平均散度进行建模.Wei[176]将SDR 和随机化逼近非凸优化的方法应用到面向分类的相位编码波形优化问题.Goodman[177]提出了一种在分类错误概率约束下,基于最大化SNR 或MI 的波形优化和序贯假设检验法,适用于2 类及以上的目标分类问题,该方案随后被扩展到MIMO 雷达[178]中.Bea[179]利用电磁仿真数据验证了Goodman[177]提出的算法在未知目标姿态条件下的性能,证明了基于目标距离像模板先验信息的分类波形,其分类准确率优于具有相同带宽的脉冲波形. 针对方位和初相均不确定的问题,纠[67]利用SDR 得到了高斯杂波环境下多类别目标分类波形的凸优化算法.
随着机器学习,特别是深度学习在目标分类方面的广泛应用且取得了显著的成效,相关技术也被应用于雷达目标分类的波形优化上[180]. 值得指出的是,大部分关于多类别目标分类波形优化问题的文献都假设目标是角度上可分的,即不同目标位于不同的波束内,使得多目标问题可以简单地转化为单目标问题的叠加,进而分别对各个目标进行单独处理,对不可分离的目标分类波形研究较少.
3.5 面向抗干扰的波形优化
从非自适应到自适应体制,雷达波形优化的本质目的都是为了抑制非感兴趣目标干扰(杂波、干扰、电子对抗等)和更好地提取目标信息[181]. 不同抗干扰措施可以针对不同干扰类型产生不同的抗干扰效果.Martone[182]结合认知雷达的PAC 机制,将现有的抗射频干扰(Radio Frequency Interference,RFI)波形自适应策略分为2 类,分别是规避(Avoid)和陷波(Notch)策略.规避策略通常是指当前信号频谱受到干扰时,将波形功率谱自适应调整到可用频谱范围内的其他不存在RFI 频带,如正交或者相关性小的频点处;陷波策略则通过调整波形功率谱,在存在窄带干扰的频点形成零陷或凹口,在保证高分辨特性的同时,抑制干扰的能量.
3.5.1 基于规避策略的抗干扰波形优化
基于规避策略的设计思想一般包含两方面含义:在设计波形时,需要考虑提高波形抗截获性能;在被截获后,能够及时调整波形.
噪声雷达信号是一类常用的抗干扰波形,一般采用随机或伪随机信号对载频进行调频调相,能提供具有图钉状模糊函数的高电磁兼容性和低截获概率性波形,相对地,其多普勒容忍性也较差. 结合线性调频波形具有刀刃型模糊函数和较好的多普勒容忍性的特点,Govoni[183]提出线性调频噪声雷达波形(Linear-FM Noise Radar Waveform),通过相位比例因子调节LFM 波形的相位和噪声的相位,并利用不同旁瓣加权函数抑制距离旁瓣,同时获得了与传统LFM 信号相当的距离-多普勒分辨率和与随机噪声波形相当的低截获概率.Li[184]将波形的模糊函数和期望模糊函数的差作为优化目标函数,通过对角加载法和循环算法,获得具有恒模特性的期望波形,随后还提出一种修正循环算法迭代求解复合波形的确定性二次相位和随机相位的组合关系,然而该算法具有初值敏感问题,并不能保证收敛到全局最优.Kulpa[185]针对频谱拥挤环境,提出一种伪随机噪声波形优化方法,可以通过调节“显著因子”权衡PSD 的形状与波形模糊函数的距离-多普勒旁瓣高度.Xu[186]提出了混沌载频捷变脉冲合成孔径雷达(Chaotic Carrier Frequency Agility Pulses,CCFAP-SAR)的概念,增强SAR 成像过程中对噪声干扰和欺骗式重复干扰的抑制能力,且成像质量优于LFM-SAR.Dai[187]利用基于雷达身份标签的混沌二进制序列对发射脉冲波形进行加密,信号在保留高分辨率特性的同时,抗干扰性能优于相位编码波形.
针对被截获后的波形调整问题,一般采用脉间波形跳频[188]或切换正交[189]的方法. Akhtar[190]通过脉间正交分块编码信号压制欺骗式转发干扰.Chen[191]提出一种适用于MIMO 雷达的正交跳频抗干扰波形优化算法,既利用跳频法避免被截获,也利用切换正交法避免转发干扰,特别是脉间灵巧转发式干扰,当正交波形组合备选集合越多,随机组合规律越复杂就越难以被干扰.Khan[192]考虑了时变正交波形在组网雷达抗干扰中的应用.
3.5.2 基于陷波策略的抗干扰波形优化
基于陷波策略的设计思想同样包含两方面含义:感知或检测RFI 占用的频带或频点;调整波形,使其在干扰频点形成零陷或凹口.
为保证系统的频谱兼容性,需要首先执行频谱感知,以获得环境频谱分布的先验知识. 对于分析环境频谱,目前常用的方法包括似然比检验、能量检验、匹配滤波检验、周期平稳检验[193]、盲信号检验[194]等. 1987年,Brandsetter[195]提出 自适 应扩 谱雷 达(Adaptive Spread Spectrum Radar,ASSR)概念,通过检测干扰所占用的频谱,并对频率编码信号对应的频段进行零陷或设计频谱凹口,最后通过解线频调的方法进行接收处理. 这种从功率谱角度出发的波形优化来抑制特定频点干扰的方法也常用于其他通信系统中[196]. Ger‑lach[197]对NLFM 脉冲的相位进行最小限度的调整,设计频谱稀疏零陷以抑制窄带有源干扰(Narrow Band In‑terference,NBI),并且对波形模糊函数产生尽可能小的影响,但没有进一步讨论该方法对波形模糊函数旁瓣特性的影响. Wu[198]将具有期望频谱特性和相关特性的波形优化问题表述为最小化波形特性和期望特性之间的差异.Palamà[199]分析了目标冲激响应与接收信号之间的互信息与外部参数(如目标、干扰和杂波功率)和雷达参数(如观测时间和发射功率)的关系,提出一种基于MI准则的频谱自适应干扰陷波和目标匹配照射波形联合优化方案.He[200]提出一种引入自相关和阻带约束的循环算法,用于设计任意波段的低相关旁瓣、低谱功率抑制的单模序列,但算法计算复杂度高难以满足实际应用需求.
基于陷波策略得到的波形频谱在带宽内通常具有不连续或稀疏特性. Mai[201]研究了稀疏频谱波形在雷达通信一体化系统中的应用,提高了通信带宽和通信速率,但是不连续频谱会产生自相关函数的高距离旁瓣.Frost[202]通过将波形PSD 建模为伯努利随机变量序列,给出频谱不连续波形的自相关序列均值和方差,推导了峰值旁瓣电平和积分旁瓣电平与频谱带宽占比的封闭表达式,可用于评估稀疏频谱波形距离旁瓣的性能.Lindenfeld[203]提出一种具有线性复杂度的宽带稀疏频谱波形设计方法,具有可调阻带带宽以及可优化距离旁瓣的特点.Patton[204]通过非线性规划方法,在降低指定阻带内的发射能量的同时,满足模糊函数和恒模约束.
3.6 面向联合多任务的波形优化
现代雷达具有较高的功能自由度,可以同时执行多个任务,但有限的雷达资源通常并不能够满足所有任务的需求. 现有的认知雷达体系架构提供了两种潜在的解决方案:一类是根据某些评价准则和环境的复杂程度,管理调度雷达资源;另一类则是利用任务间的关联对信息进行共享和最大化利用,实现多任务联合处理. 正如第2 节所述,不同雷达任务之间存在耦合性,这种耦合性不仅体现在评价指标上的相互关联,也体现在不同任务间信息的可复用性. 并且这种可复用性一般不受任务认知层次的限制,如图2 所示,例如经过检测任务得到的信息同时流向跟踪与分类,既可以影响跟踪任务,也可以影响分类结果.
这种耦合性也促进了雷达接收端联合多任务处理的研究和发展,如联合跟踪与分类(Joint Tracking and Classification,JTC)、联合检测与跟踪(Joint Detection and Tracking,JDT)[205]、联合检测、跟踪与分类(Joint De‑tection,Tracking and Classification,DTC)[206]、联合跟踪与成像[207]、联合检测与成像等. 对于联合检测与跟踪任务,一种常用的算法被称为检测前跟踪(Track-Be‑fore-Detect,TBD),该算法通过沿航迹积累多帧观测的目标能量,从而得到更高的检测判决SNR.
在CTR的框架下,Liu[208]引入了指数嵌入族估计法逼近未知测量噪声的分布,提高了基于TBD 的联合检测与跟踪波形优化的稳健性. Piwowarski[209]最小化跟踪滤波器的预测协方差时,根据不同状态变量的重要性,提出了最小化加权预测MSE的跟踪波形优化方法.Zhang[210]将基于SNR 的检测波形优化方法与Dai[106]的跟踪波形优化方法进行有机结合,提出了一种能够同时提升目标估计和检测性能的联合检测与跟踪波形优化方案. 对于联合跟踪与成像任务,Stambouli[211]在认知SAR 的框架下,结合数字波束形成与波形参数的动态调整,提出一种具有跟踪和成像能力的认知系统. 而对于联合检测与成像任务,Giusti[212]提出一种基于规则的认知雷达架构,通过定义任务性能指标和动态规则(Rules)驱动认知雷达采取期望的行动. 雷达资源、波形可调参数、先验知识和期望性能的关联性被纳入规则的范畴,用于权衡所有元素对认知雷达感知环境的影响. Giusti[212]设计了基于该架构的联合检测与成像的波形优化方法,并在实测数据上得到了验证. Kurd‑zo[213]从联合多任务波形库设计的角度利用积分旁瓣电平(Integrated Sidelobe Level,ISL)和主瓣宽度的比值作为适应度函数,提出了一个能够设计面向不同雷达任务的NLFM波形的神经网络.
在优化理论框架下,面向联合多任务的波形优化,其中一个重要的问题就是如何权衡多个任务性能准则的相对重要性,早在19 世纪运筹学中就提出了利用MOP 帕雷托最优性进行准则间的平衡[63]. 在雷达波形优化应用中,常用的多准则优化求解方法主要有启发式的多目标进化算法(Multi-Objective Evolution Algo‑rithm,MOEA)[214]和标量化方法[215]. 随着多功能雷达的发展,未来的雷达波形必然需要同时能够适应联合多任务需求,不仅现有准则函数之间互容或互斥作用机理的理论体系还需要进一步完善,还需要为联合多任务性能表征提供新的理论依据.
4 总结与展望
4.1 总结
认知雷达能够持续与环境交互,自组织地感知环境并学习探知策略,以优化系统的探测性能. 认知雷达是现代雷达迈向智能化感知的一个重要阶段,具有广泛的研究意义和应用前景. 本文分别从检测、跟踪、成像、分类任务以及抗干扰的波形设计角度出发,对面向不同雷达任务波形设计的主要研究内容、研究方向和研究进展进行了综述,以期更全面地对为面向单一任务的波形设计提供纵向方法对比;此外,还简要地介绍了面向联合多任务的波形优化研究进展,从雷达任务耦合的角度,分析了联合多任务处理的潜在优势.Gius‑ti[212]指出,对于在特定场景下,认知雷达不一定具有比传统自适应雷达更好的性能,但可以肯定的是,拥有更高灵活性认知雷达能够适用于任何场景而不受设计的限制. 总之,当前认知雷达系统还处于研究探索阶段,还没有真正意义上从“自适应”迈入“认知”,但是随着研究的不断深入,认知雷达的优势将逐步凸显. 分析认知雷达波形优化潜在的优势和面临的挑战,值得关注的研究方向可以概括为:知识有效性评价、人工智能认知波形优化、通用度量准则、知识辅助的高效优化算法等.
4.2 展望
4.2.1 知识有效性评价
Guerci[216]详细介绍了认知雷达知识库包含的内容,根据数据来源划分为内部数据(雷达本地处理后获得的知识,如合成孔径雷达图像、跟踪数据等)和外部数据(从其他传感器或系统获得的知识,如数字地形、陆地覆盖类型等).Haykin[90]提出带记忆机制的架构能保存并自动更新雷达每一次与环境交互和信号处理后的知识,然而并没有进一步指出如何对长短期记忆进行有效区分和利用. 由马尔科夫过程的特性可知,与当前时刻相关的知识仅在当前时刻的时间邻域内,过去对当前的影响微乎其微;同时,目标或环境的统计分布特性又需要从较长时间范围内进行总结. 因此,如何正确评价并高效使用认知雷达的知识是一个亟待解答的问题.
4.2.2 人工智能认知波形优化
人工智能近年来广泛应用于计算机视觉、自然语言处理等领域. 特别是深度学习算法,尽管其可解释性还处于研究和发展过程中,但是在大数据技术支撑下的端对端处理上,具有无可比拟的优势. 将人工智能算法应用于认知波形优化需要考虑至少3个方面问题:一是网络表达能力问题,即何种网络结构能够有效逼近所需的目标函数或拟合认知发射和认知接收过程;二是如何保证网络总能搜索到最优解,或如何避免网络陷入局部最优;三是如何评价模型的有效性及对实际问题的泛化性能.
4.2.3 通用度量准则
模糊函数是当前研究中常用的波形通用评价工具,有效描述了发射波形的自相关性质.Fisher 信息能够将波形参数和估计性能联系起来,给出了一种波形AF 在原点局部特征表征方法,而基于信息论的相对熵描述则进一步考虑了全局特性. 其共同点在于均提供了与具体算法无关的波形性能通用度量方案.
信息几何将概率论、信息论和统计学中的许多重要概念视为概率分布空间中的几何结果,采用微分几何方法研究其上的性质,从而将概率论和信息论中的基本问题几何化,赋予其内在的几何本质[217]. 在信息论的基础上,信息几何可以从几何信号处理的视角为波形优化提供新的设计思想. 王[101]通过分析基于模糊函数的名义分辨率的缺陷,引入了在信息几何理论框架下定义的信息分辨率和信息分辨率界限,使得基于实际分辨率的波形优化能够更全面地对波形和目标进行评估. 李[218]详细研究了基于黎曼几何的MIMO 雷达认知波形优化问题.
4.2.4 知识辅助的高效优化算法
雷达波形优化通常被等效表述为波形的参数寻优问题. 参数空间的大小通常会对优化算法的计算效率产生较大的影响. 蝙蝠“回声定位”系统能够同时对声波信号的强度(声压级)、方向、频率成分、频率调制方式、持续时间等进行实时地调整,使其能够快速感知环境并捕获目标. 这种高自由度的参数选择使蝙蝠能够根据任务需求发射不同种类的信号(如纯恒频、线性调频、非线性调频),具有更灵活的场景适应性. 认知雷达的自治能力允许其基于知识辅助进行波形类型与参数空间的灵活调整,从而更好更高效地满足复杂动态环境探测和多类射频系统共存的需求.
