基于自编码器和超图的半监督宽度学习系统

王雪松，张翰林，程玉虎

1 引言

Chen 等［1］提出的宽度学习系统（Broad Learning System，BLS），亦称宽度网络，是一种由输入层、中间层（包括映射特征和增强节点两个部分）和输出层构成的前馈神经网络. 因其简洁灵活的网络结构、高效的学习过程等优点，而被广泛应用于众多领域. Sui 等［2］使用BLS识别动力学未知的不确定系统，提出了一种随机有限时间量化控制方法.Chu等［3］使用惩罚系数来约束每个样本对模型的贡献，提出了一种加权BLS 并将其用以解决工业过程中的噪声和离群值问题.Han等［4］提出了一种用于大规模混沌时间序列建模的宽度学习系统，解决了动力学系统建模中利用混沌系统演化信息进行时间序列预测的问题.

然而，上述方法均为监督型宽度学习方法，在标记样本有限的情况下，往往存在泛化性不足的问题. 半监督学习是一种可以同时使用少量标记样本和大量无标记样本进行学习的方法. 因此，半监督宽度学习的研究引起了学者的广泛关注.Kong等［5］将常规BLS进行半监督拓展，提出了一种基于类别概率框架［6］的半监督BLS（Semi-supervised BLS，SBLS），用于解决标记样本较少情况下的高光谱图像分类问题. 但是，SBLS非常依赖伪标签的质量，被错误标记的样本将严重影响算法的性能.Zhao 等［7］将BLS 和流形正则化框架［8］相结合，提出了一种基于图的半监督BLS（ss-BLS）. ss-BLS 通过构造标记样本和无标记样本的拉普拉斯矩阵，将流形正则化项加入BLS的目标函数中，并使用岭回归算法求解构造的目标函数. 传统的图模型［9］虽然可以在低维空间中保持数据原有的流形结构，但是该模型仅考虑了两个数据间的成对关系，无法准确地表达数据间的复杂高阶流形关系. 为此，本文引入超图模型［10］，提出一种基于超图的半监督宽度学习系统. 此外，常规BLS中通常采用的线性稀疏特征提取方法难以挖掘数据的本质特征，从而限制了BLS性能的发挥. 自编码器［11］因其在无监督情况下，仍能够学习到数据的复杂非线性特征而被广泛应用于入侵检测［12］、目标检测［13］和辐射源识别［14］等领域. 众所周知，良好的特征提取方法对于提高模型的性能至关重要. 为此，本文将自编码器与BLS相结合，用以提高BLS对复杂非线性特征的提取能力.

综上，本文提出了一种基于自编码器和超图的半监督宽度学习系统（Autoencoder and Hypergraph-based Semi-supervised Broad Learning System，AH-SBLS），主要工作包括：（1）将超图模型引入到常规监督型BLS中，以充分挖掘包括标记样本和未标记样本在内的所有样本之间的复杂流形关系；（2）利用多层自编码器提取数据的复杂非线性特征，从而进一步提升AH-SBLS的泛化性能.

2 基于自编码器和超图的半监督宽度学习系统

如图1 所示，AH-SBLS 主要包括4 个部分：（1）基于自编码器的特征提取. 首先，使用含标记样本和无标记样本在内的全部样本训练自编码器；然后，将自编码器特征层中的特征作为AH-SBLS 的特征节点；（2）特征增强. 对特征节点进行非线性映射以实现宽度拓展，并将得到的增强节点与特征节点进行堆叠；（3）超图构造.同样利用全部样本构造半监督超图，并计算超图的拉普拉斯矩阵；（4）目标函数构造. 根据得到的拉普拉斯矩阵进一步构造超图正则项，并与常规BLS 的目标函数相结合. 通过对该目标函数进行求解，可以得到输出层权重，进而实现对无标记样本的类别预测.

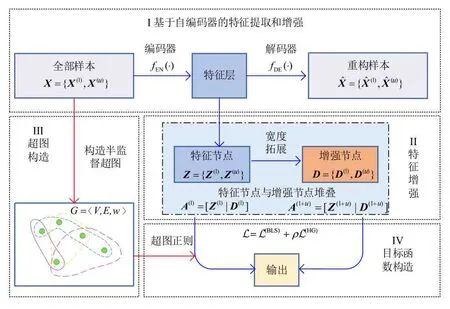
图1 AH-SBLS模型结构图

2.1 基于自编码器的特征提取

图1中的自编码器由编码器fEN(∙)和解码器fDE(∙)两部分组成，其中，编码器旨在将全部样本映射到特征层以得到编码特征Z，解码器的目标为对编码特征进行重构. 给定输入样本矩阵X，则编码器的计算过程为：

Z=fEN(X)=ζ(XWEN+bEN) （1）

其中，ζ(∙)为编码器的激活函数，WEN和bEN分别为编码器的权重和偏置. 类似地，令解码器的权重和偏置分别为WDE和bDE，激活函数为δ(∙)，则解码器的输出可以表示为：

一般而言，自编码器的损失函数通常为均方误差损失. 均方误差损失函数可以表示为：

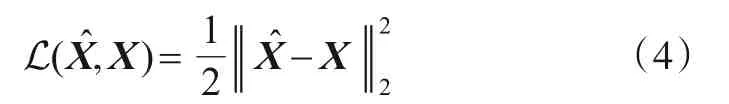
其中，参数W，b可以使用梯度下降法［15］来更新，其更新规则为：

其中，α为学习率，用来控制参数更新的步长. 梯度下降法常用的优化算法有SGD（Stochastic Gradient De‑scent）、RMSprop（Root Mean Square prop）和Adam（Adaptive moment estimation）［16］等，鉴于Adam 具有较快的收敛速度，这里将其用于自编码器参数的更新. 在完成自编码器参数的更新后，将自编码器的编码特征Z作为AH-SBLS模型的特征节点.

2.2 特征增强

AH-SBLS 的第II 部分为特征增强，旨在利用随机生成的权重对特征节点进行映射，实现快速非线性宽度拓展，其计算过程为：

d=ξ(Zwd+bd) （7）

其中，ξ(∙)为tansig 激活函数，wd为随机的线性稀疏权重，bd为增强节点的偏置. 设共有m组增强节点，则D=[d1,…,dm]，将特征节点和增强节点堆叠，得到输入样本的特征矩阵A=[Z|D].

2.3 超图构造

在半监督学习中，虽然无标记的样本没有标记信息，但是无标记样本与标记样本包含相同的数据分布信息，所以利用无标记样本能够帮助建立更具泛化性的分类模型. 为了利用无标记样本，必须假设无标记样本与类别标记之间的联系. 基于光滑度假设，图模型被提出用于解决半监督学习问题. 然而，常规图模型只能描述数据之间简单的二元关联关系，无法描述数据中复杂的单对多或多对多的多元关联关系，从而难以对数据的复杂流形结构进行充分描述.

相对于常规图，超图可以更加准确地描述存在多元关联的对象之间的关系. 在常规图中，一条边包含两个顶点，而在超图中，一条超边可以包含多个顶点，从而对多个数据点之间的关系进行描述. 给定N个输入样本，则输入样本矩阵可以表示为X=[x1,x2,…,xN].AH-SBLS 将每个样本x作为超图顶点和一条超边的中心，使该超边连接该样本最近邻的k个样本，以此来构造样本超图模型. 将超图模型表示为三元组G=其中，V={v1,v2,…,vN}为顶点的集合，E={e1,e2,…,eN}为超边的集合，w为超边的权重集合. 超图模型可以通过构造点边关联矩阵Hve∊RN×N来建立顶点和超边的关系，Hve中的元素可通过下式计算：

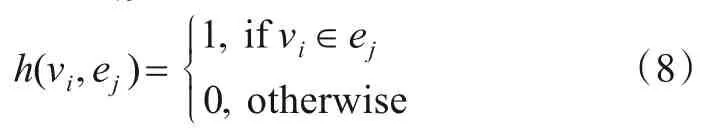
样本之间的距离度量函数通过下式计算：

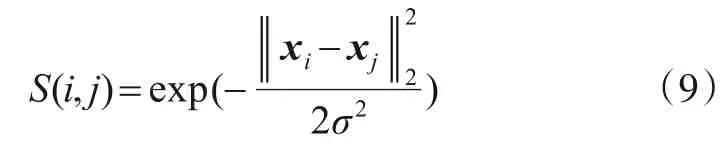
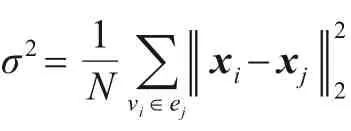
其中，是控制函数S(i,j)径向作用范围的超参数. 定义超边权重向量为，则每条超边的权重可以通过下式来计算：

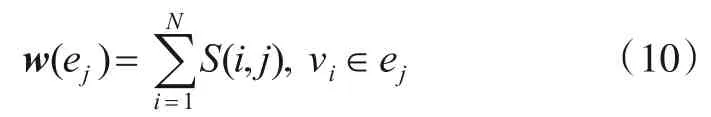
定义顶点的度向量为dv∊R1×N，用于描述每个顶点的超边权重. 则顶点的度的计算公式为：

定义超边的度向量δe∊R1×N，用于描述每条超边包含的顶点个数. 则超边的度计算公式如下：

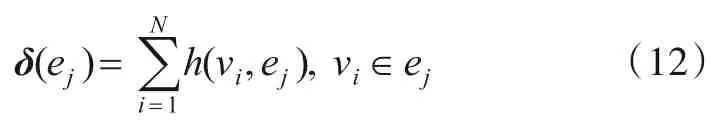
通过上述讨论，可以定义超边的权重矩阵We=diag(we)∊RN×N，顶点的度矩阵Dv=diag(dv)∊RN×N和超边的度矩阵De=diag(δe)∊RN×N三个对角矩阵. 根据光滑度假设，距离接近的样本应该拥有相同的标签，亦即同一条超边应连接相同标签的样本. 构造超图损失函数：̂为模型的预测样本标签. 将式（13）表示为矩阵形式：

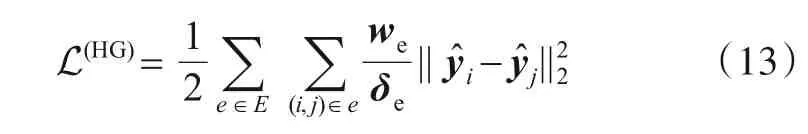
其中

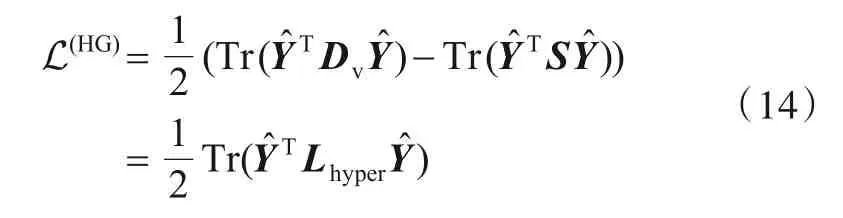
其中，超图拉普拉斯矩阵Lhyper的计算公式为：

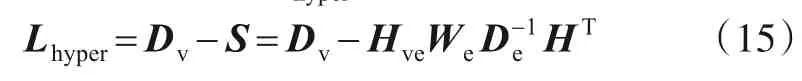
2.4 目标函数构造及求解

给定l个标记样本X(l)∊Rl×r和u个无标记样本X(u)∊Ru×r，则全部样本为X(l+u)∊R(l+u)×r. 其中，r为样本的维数. 将标记样本的标签表示为矩阵形式Y(l)，模型的预测标签矩阵记为Ŷ，标记样本的特征矩阵记为A(l)，全部样本的特征矩阵记为A(l+u). 常规BLS模型的目标函数为：其中，Wo为输出层权重，λ∊[0,1]为结构风险项系数.将式（14）作为超图正则项与式（16）相结合，得到AHSBLS的目标函数：其中，ρ∊[0,1]为超图正则项的缩放因子. 令0，即可求解式（17），得到AH-SBLS 模型输出层权重的计算公式：

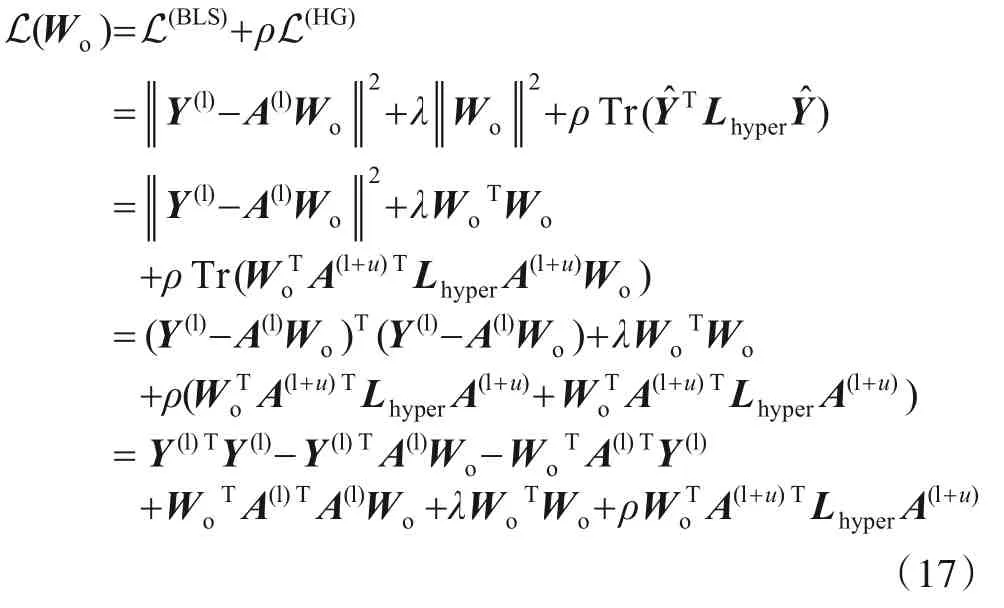
Wo=(A(l)TA(l)+λI+ρA(l+u)TLhyperA(l+u))-1A(l)TY(l)（18）

2.5 算法流程

所提AH-SBLS的流程如算法1所示：

3 实验与分析

3.1 数据集

为验证AH-SBLS 的性能，选择人手写数字数据集MNIST（Mixed National Institute of Standards and Tech‑nology）和三维玩具模型数据集NORB（New York Uni‑versity Object Recognition Benchmark）进行实验.MNIST数据集［17］由来自250 位不同的人手写的0~9 共十个数字70000 幅图像构成，每张均为28×28 像素的灰度图像. NORB 数据集［18］是一个比MNIST 特征更为多样的数据集，它包含50 种玩具模型的图像，共5 类：四足动物、人物、飞机、卡车和汽车. NORB 数据集中的所有48600 幅图像是用两个摄像机在6 个光照条件，9 个仰角和18 个方位角对玩具模型拍摄的灰度图像，由2×32×32个像素组成.

3.2 实验结果及分析

为分别考查自编码器和超图对AH-SBLS 性能的影响，将AH-SBLS 及其3个特例包括A-BLS1（仅使用单层自编码器进行特征提取的监督型学习）、A-BLS（仅使用多层自编码器进行特征提取的监督型学习）、AHSBLS1（使用单层自编码器进行特征提取且利用超图实现半监督学习）与下述6种方法进行对比，包括：堆栈自编码器（SAE）［11］、抗噪堆栈自编码器（SDA）［19］、深度置信网络（DBN）［20］、深度玻尔兹曼机（DBM）［21］、BLS［1］和ss-BLS［7］. 实验设置：（1）对于监督型方法，分别从MNIST和NORB数据集中选择6000个和4860个样本作为训练样本，剩余样本用于测试；（2）对于半监督型方法，从MNIST数据集中每类选择100个标记样本和900个无标记样本，从NORB 数据集中每类选择600 个标记样本和4260个无标记样本，其余样本用于测试；（3）SAE、SDA、DBN、DBM 和BLS 的超参数及实验结果直接取自文献［1］. 所有宽度学习系统的超参数均采用网格搜索法确定，具体设置情况如表1、表2所示，其中“-”表示该参数不取值. 在AH-SBLS 中，参数λ和ρ分别控制岭回归正则项和超图正则项在目标函数中的权重. 如果λ=0，岭回归方法就退化为了最小二乘. 如果ρ=0，超图正则项就失去了作用.k为超图的最近邻样本数. A-BLS 和AH-SBLS 均采用一个5 层自编码器，在MNIST 和NORB数据集上每层的节点个数分别为600-500-50-500-600、1800-550-300-550-1800；（4）所有实验均在配备有Inteli7 2.4 GHz CPU，GTX1080Ti GPU 的计算机上进行. 为消除随机因素的影响，所有实验重复5次并取平均值.

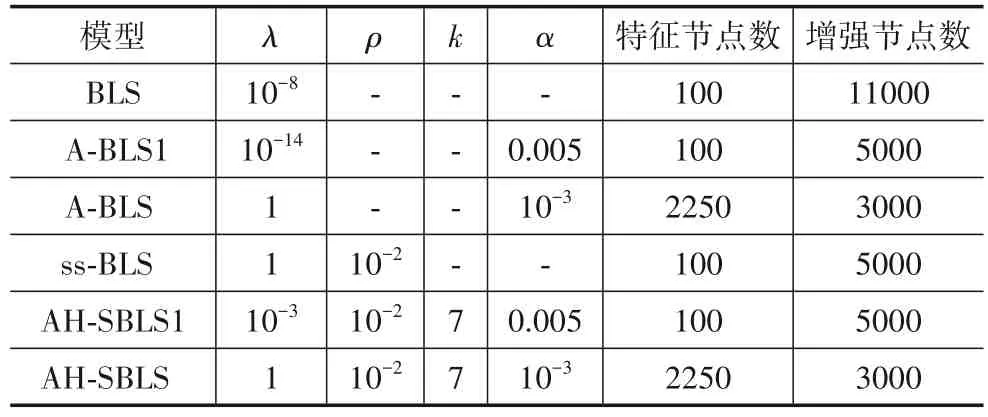
表1 宽度学习系统的超参数设置（MNIST数据集）

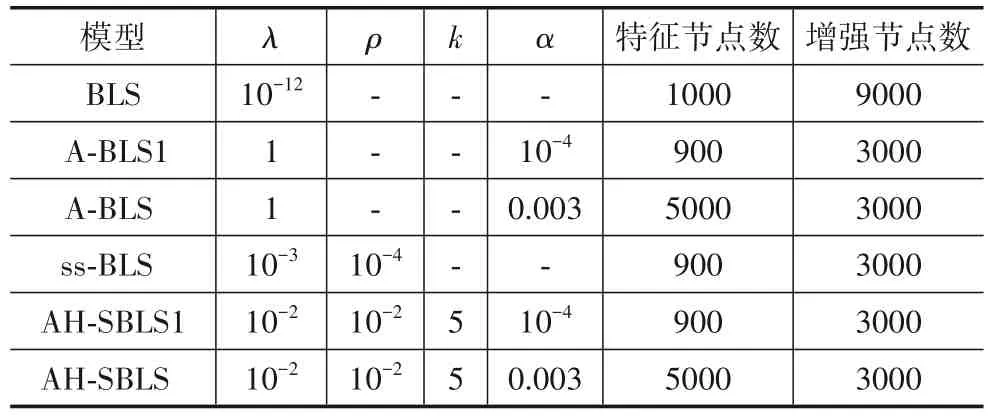
表2 宽度学习系统的超参数设置（NORB数据集）

表3、表4 给出了各方法在MNIST 和NORB 数据集上的图像分类实验结果对比，可以看出：

（1）在所有监督型宽度学习方法中，A-BLS 的分类精度最高，A-BLS1 次之. 这印证了BLS 线性稀疏特征提取方法存在表征瓶颈，并且由自编码器提取的非线性特征要比线性稀疏特征更能反映出样本在特征空间中的真实分布. 在所有监督型学习方法中，A-BLS 同样取得了最高的分类精度. 这是因为多层的自编码器可以学习到样本不同层次的特征表示，通过组合不同层次的特征，A-BLS能够实现特征空间与标记空间之间更准确的映射；

（2）从时间上分析，在所有监督型宽度学习方法中，BLS、A-BLS1 和A-BLS 的耗时均相对较少. 这是因为宽度网络的输出层参数可以直接通过广义逆矩阵的计算得到，且模型的结构较为简洁. 同为宽度学习方法，BLS在MNIST数据集上的耗时最短，其次为A-BLS1. 这是因为训练自编码器比直接提取线性稀疏特征需要更多的时间. 在NORB 数据集上，A-BLS1 为最快速的模型，比BLS 耗时更少. 这是因为A-BLS1 使用了更少的特征节点和增强节点.

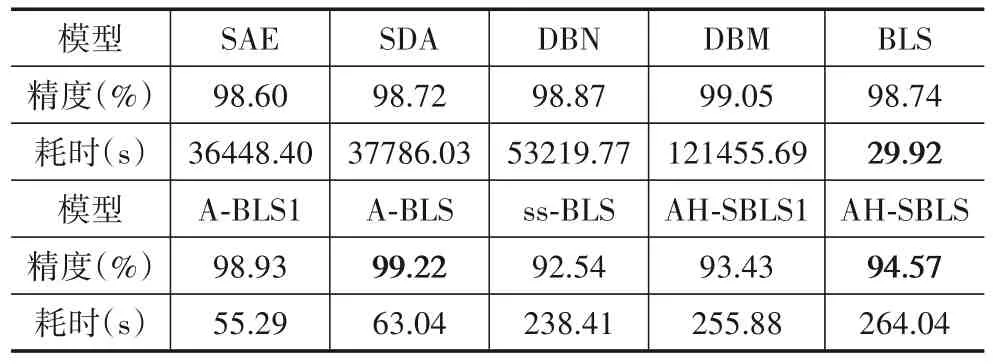
表3 图像分类结果对比（MNIST数据集）

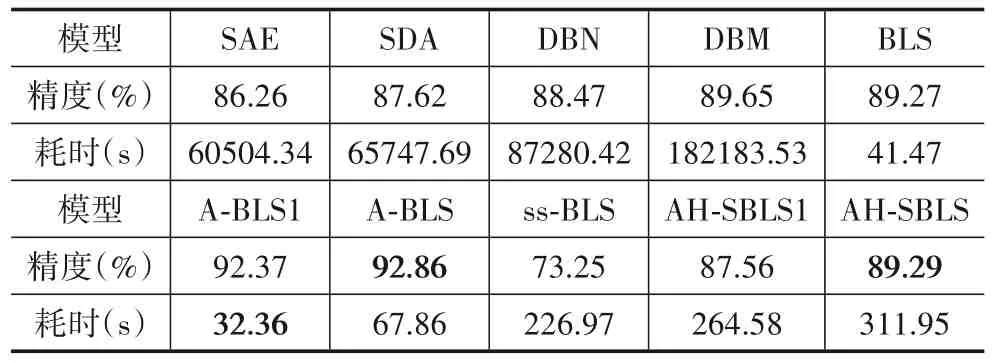
表4 图像分类结果对比（NORB数据集）

（3）同为半监督宽度学习方法，相较于ss-BLS，AHSBLS1（特征节点数与增强节点数与ss-BLS 相同）能够以很少的训练时间为代价，取得更高的分类精度. 同时，AH-SBLS 模型仍是精度最高的模型，这一结果充分说明了超图模型比常规图模型更能反映样本之间的真实联系.

为分析标记样本的数量对AH-SBLS 分类精度的影响，通过设置不同标记样本个数进行实验，并选择ss-BLS 和AH-SBLS1 作为对比方法. 在MNIST 数据集中，标记样本的数量由每类10逐渐递增为100. 在NORB数据集中标记样本的数量由每类100 逐渐递增为600. 实验结果如图2所示，由图可知：

（1）在两个数据集上，随着标记训练样本量的增加，ss-BLS、AH-SBLS1 和AH-SBLS 的分类精度均逐渐提高. 这是因为对于半监督学习方法来说，利用更多的标记样本能够帮助学习到泛化能力更强的分类模型；

（2）标记训练样本数量相同的情况下，AH-SBLS 能够取得最高的分类精度，而且拥有相同特征节点和增强节点数的AH-SBLS1 的分类精度仍高于ss-BLS. 这印证了相比于常规图，超图能够通过对标记样本和无标记样本之间的复杂流形关系的建模，帮助获取更高的分类精度.

3.3 特征t-SNE可视化

为了直观地展示AH-SBLS 模型中自编码器的特征提取效果，在MNIST 和NORB 两个数据集上使用t-SNE方法［22］对自编码器提取的特征进行了可视化. 该实验在两个数据集上每类均随机选取200 个样本. 对于拥有多层特征层的AH-SBLS 模型，只显示中间维数最少的特征层的可视化结果. 实验结果如图3、图4所示.

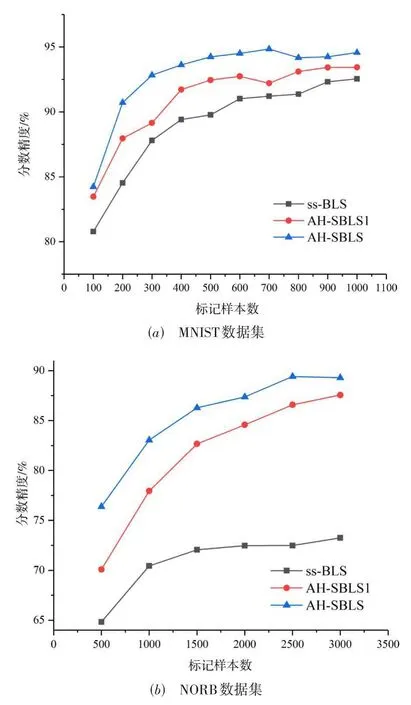
图2 标记样本数量对分类精度的影响

可以通过比较原始图像的分布和模型提取特征的分布来评价模型的特征提取效果. 由图3、图4 可知：（1）在MNIST 数据集上，虽然大多数数字都可以被AH-SBLS 模型准确地区分开，但无论是原始数据还是模型提取的特征，数字“4”和“9”在图中的分布均非常接近，说明这两个数字具有非常相似的特征，将它们区分开来的难度较大. 同样在图4 中，汽车和卡车的分布也具有这样的特点. 汽车和卡车均属于“车”，拥有较多的相似特征，将它们区分开来的难度较大也是符合直觉的；（2）相较于原始数据和BLS 提取的特征，AH-SBLS 提取得到的特征不同类别之间有了更大的间距，同类特征分布地更加密集，并且离群的数据点较少. 这说明利用AH-SBLS 提取的多层非线性特征具有更强的可分性，进而帮助宽度学习系统实现更加准确的类别预测.

图3 特征t-SNE可视化（MNIST数据集）

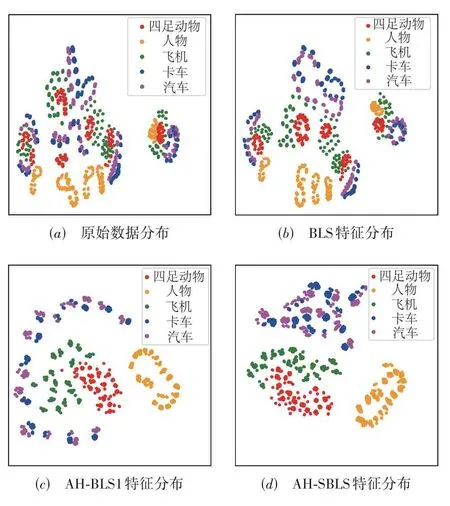
图4 特征t-SNE可视化（NORB数据集）

4 结论

随着计算机技术的迅猛发展，人们将获取越来越多的无标记数据，而有标记样本需要人工对样本进行标记，因而有标记样本的获取相对比较困难而且代价昂贵. 在标记样本极少的情况下，常规的宽度学习系统难以取得良好的表现，很容易陷入对少量样本的过拟合或者及对目标任务的欠拟合. 因此，将少量的标记样本信息和大量的无标记样本信息加以综合利用的半监督学习有着广泛的需求. 本文提出的AH-SBLS 模型将超图结构引入到常规监督型BLS 中，不仅能够实现半监督学习，而且充分考虑了数据之间的复杂多元关系.此外，多层自编码器的使用有助于提取到输入数据的本征特征，从而进一步提升半监督BLS 的泛化性能.MNIST 和NORB 两个数据集上的实验结果验证了AHSBLS的可行性和有效性.