缝洞型岩溶热储流动传热耦合数值模拟

姚 军 张 旭 黄朝琴 巩 亮 杨文东 李 阳

中国石油大学（华东）油气渗流研究中心

0 引言

碳酸盐岩岩溶热储是一种典型的地热储层，具有出水量大且地热利用后的尾水易于回灌的优势，是我国最具开发利用潜力的主力地热储层[1]。我国碳酸盐岩的分布总面积占陆地面积的三分之一，裸露面积约为90×104km2，隐伏面积达250×104km2以上[2]。处于较高热流值背景下的几大主要区域有：渤海湾盆地、鄂尔多斯盆地、苏北盆地、江汉盆地、楚雄盆地、兰坪思茅盆地、昂拉仁错盆地和羌塘盆地[2]。碳酸盐岩热储资源量占我国水热型地热资源总量的70%～80%[3]。由于区域构造运动和岩溶作用，岩溶热储内发育大量的裂缝及溶洞，裂缝长度跨越从厘米级到千米级，天然裂缝网络处于连通或不连通状态；溶洞尺寸跨越从厘米级到米级，空间分布呈现与裂缝相连或分离特征[4-7]。因此，与孔隙型或裂缝型热储相比，缝洞型热储的储集空间类型多样（孔、缝、洞），具有显著的多尺度、强非均质特征，流体流动既有多孔介质区域（岩石基质及裂缝系统）的渗流又有溶洞区域的自由流[8]。目前，针对孔隙型和裂缝型热储的热采动态已进行大量数值模拟研究[9-30]，但由于缝洞型热储内具有复杂的多尺度、强非均质、多流态特征，缝洞型热储热采过程中涉及的流动、传热特征及热采动态尚不清晰，亟需建立一套适用于缝洞型岩溶热储流动传热模拟的理论和方法。

当前国内外学者在缝洞型碳酸盐岩渗流理论方面做了大量的工作，发展了等效连续介质和离散介质数学模型，其中等效连续介质模型又可分为等效单重介质模型和三重介质模型。等效单重介质模型是将整个缝洞型介质视为一个连续体，通过等效参数表示其非均质性[31-32]。因此，该模型具有计算效率高、参数求取简单等优点。原理上，等效单重介质模型仅适用于缝洞系统发育程度高、连通性好的储层。另外，无法考虑裂缝网络连通性和其他裂缝属性对流动过程的影响。三重介质模型是双重介质模型的扩展和延伸，将缝洞型介质划分为三个平行的连续介质系统，即低渗透基岩、高渗透裂缝和溶洞，通过窜流函数有机耦合各系统[33-34]。三重介质模型能够有效刻画缝洞型介质中的优先流现象，并充分考虑基岩、裂缝和溶洞系统间的物质交换，比较符合实际。但该模型对缝洞网络几何形态过于简化，且窜流函数也难以确定，不适用于离散分布的大尺度裂缝和溶洞的模型，具有一定的局限性。离散介质模型是将裂缝和溶洞的几何结构进行显式表征，能够准确描述缝洞型介质中的流体流动过程[8,35-36]。目前，国内外仅对缝洞型介质内流体流动进行了研究，对于其内部流动换热机理及热采特性的研究，未见相关的研究报道。对此，本研究建立了基于离散缝洞网络方法的热流耦合模型，研究了裂缝及溶洞的多尺度、强非均质及多流态特征对缝洞型热储内流动和传热过程的影响，对标裂缝型热储开发动态，系统分析缝洞型岩溶热储开发特征，以期为其高效开发提供理论基础。

1 缝洞型岩溶热储热流耦合模型

1.1 缝洞网络模型

该研究中，通过直线段和圆分别表征裂缝和溶洞几何形状[32,37]，如图1所示。

图1 缝洞型岩溶热储及离散缝洞网络示意图

天然缝洞系统通常呈现显著的多尺度特征，裂缝长度和溶洞直径服从幂律分布，其概率密度函数n(lf)、n(lc)表达式[38-42]：

式中l表示裂缝长度或溶洞直径，m；下标f和c分别表示裂缝和溶洞；α是密度项；a表示幂律尺寸指数。

该模型唯一的特征长度参数是裂缝或溶洞最小尺寸和最大尺寸，即lmin和lmax。大量现场数据表明，裂缝和溶洞的长度指数a分布范围分别介于1.5～3.5和2.2～2.6[41-42]。

1.1.1 裂缝密度与连通参数

式中γf表示裂缝密度，1/m，为单位模型面积内裂缝长度之和，与裂缝长度密度分布函数有关[43-44]；L表示模型尺寸，m；pf表示连通参数，表征裂缝网络连通程度[37]。

pf值越大，系统连通程度越高。当大于连通阈值（pfc）时，裂缝网络是连通的；反之，则不连通。对于二维随机裂缝网络，pfc具有尺度无关性，pfc值在较小的范围内变化，即5～7之间，也就是pfc=6±1。

1.1.2 溶洞孔隙度

溶洞孔隙度（φc）表示单位模型面积内溶洞面积之和[35, 45]：

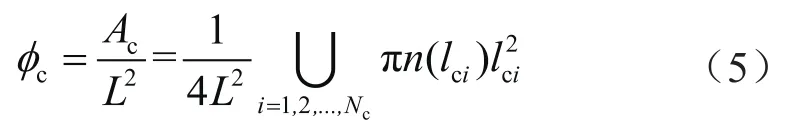
式中Ac表示模型内溶洞总面积，m2；U表示求和运算符；Nc表示溶洞总数。

1.2 流动传热耦合模型

基于离散缝洞网络方法，建立适用于模拟缝洞型岩溶热储内流体流动及热量传递的热流耦合模型。离散缝洞网络方法将缝洞型岩溶热储视为由岩石基质、裂缝系统和溶洞系统组成的储层，其中裂缝和溶洞嵌套于岩石基质中，相互分离或连接形成缝洞网络（图1）。岩石基质和裂缝系统视为多孔介质区域，溶洞系统视为自由流区域。在流动模拟中，考虑不同流动区域间的流动耦合，即多孔介质区域渗流与溶洞区域自由流耦合，渗流区域满足Darcy方程，自由流区域满足Navier-Stokes (N-S)方程，两区域交界面采用Beavers-Joseph-Saffman(简称BJS)条件进行流动耦合[46-48]。在传热模拟中，考虑热传导和热对流两种传热方式，热岩石基质与冷流体在缝洞界面上热量交换满足局部非热平衡效应[9]。

1.2.1 流动方程

基质内渗流方程[9]：

式中ρf表示流体密度，kg/m3；Sm表示基质储水系数，1/Pa；pp表示多孔介质区域流体压力，Pa；t表示时间，s；um表示基质内渗流速度，m/s；km表示基质渗透率，mD；ηf表示流体动力黏度，Pa·s；g表示重力加速度，m/s2；z表示沿重力方向单位向量。

裂缝内渗流方程[9]：

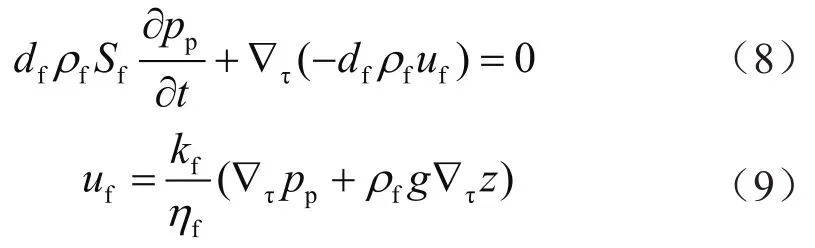
式中df表示裂缝开度，m；Sf表示裂缝内储水系数，1/Pa；uf表示裂缝内渗流速度，m/s表示沿裂缝切向方向的梯度算子；kf表示裂缝渗透率，mD。

溶洞内流动方程[8,35]：

式中uc表示溶洞内流动速度，m/s；σf表示溶洞内流体应力，Pa；I表示单位张量表示流体应变张量；pc表示溶洞内流体压力，Pa。

多孔介质区域与自由流区域交界面耦合流动满足BJS边界条件[46-48]：

式中up表示多孔介质内渗流速度，m/s；K表示多孔介质内渗透率张量，mD；n、τ分别表示多孔介质与溶洞界面单位法向向量和单位切向向量；β表示切向阻力系数。

基于Darcy定律估算缝洞型岩溶热储的等效渗透率（keq）：

式中Qout表示出口端的体积流量，m2/s；累加项（∑）表示出口端裂缝的流量计算；积分项（∫）表示出口端岩石基质和溶洞的流量计算；pin、pout分别表示注入端和出口端压力，Pa。

1.2.2 传热方程

基质内传热方程[9]：

式中 (ρC)eff表示有效热焓，J/(m3·K)；λeff表示有效导热系数，W/(m·K)；下标s和f分别表示固体和流体；ε表示基质孔隙度；C表示比热容，J/(kg·K)；λ表示导热系数，W/(m·K)；q表示基质与流体在裂缝或溶洞界面上的换热量，W/m3。

裂缝内传热方程[9]：

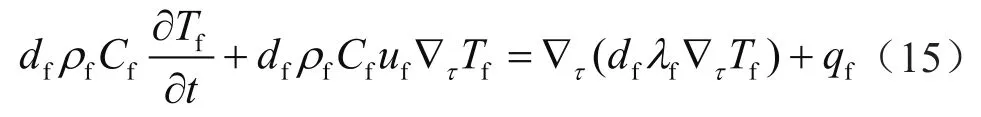
式中qf=h(Ts－Tf)为牛顿换热公式，表示单位面积上基质与流体在裂缝面上的换热量，W/m2；h表示对流换热系数，W/(m2·K)。

流体在裂缝与溶洞相交处满足温度相等。溶洞内传热方程：

式中Tc表示溶洞内流体温度，℃；qc表示单位面积上基质与流体在溶洞界面上的换热量，W；A表示溶洞单元与基质单元接触面积，m2；vc表示与基质单元接触的溶洞单元体积，m3。

出口端平均温度（Tout）计算公式为[15]：

整体采热量（Wtotal）为[18]：

式中Qm表示出口端质量流量，kg/(m·s)；hpro、hinj分别表示开采流体和注入流体比焓，J/kg。

可采热量（Wr）为：

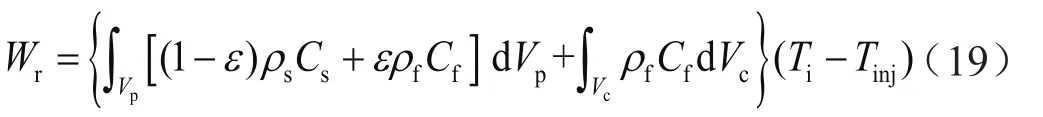
式中Vp、Vc分别表示多孔介质区域体积、溶洞区域体积，m3；Ti、Tinj分别表示储层初始温度、注入流体温度，℃。

热储整体热采率（γglobal）为：

笔者基于有限元软件COMSOL Multiphysics进行二次开发实现缝洞型岩溶热储热流耦合模型的数值求解。基于Matlab编程生成满足规定的概率分布的离散缝洞网络模型，然后基于COMSOL Mutiphysics with Matlab将缝洞网络几何模型导入有限元软件进行求解。采用无厚度平面单元模拟裂缝，实体单元模拟基质和溶洞。基于达西流和蠕动流模块求解多孔介质和溶洞区域内流体流动；基于多孔介质传热模块求解多孔介质区域换热过程，自定义偏微分方程模块求解裂缝和溶洞内换热过程；进一步考虑流体与基质岩块在裂缝和溶洞界面上的质量和能量交换，编写相应的程序代码，并嵌套在软件中实现基于离散缝洞网络方法的热流耦合模型求解。与连续介质模型相比，离散介质方法可以通过流量等效等方法，对裂缝进行降维处理，简化为1维线单元，并将裂缝开度耦合到控制方程中，这样可以避免在裂缝区域进行大量的精细网格剖分，降低计算量，提高计算效率。

1.2.3 流动模型验证

该研究中渗流—自由流耦合模型采用经典的Beavers—Joseph实验模型进行验证，如图2-a所示。考虑多孔介质区域渗流及自由流区域流动为稳定层流，注入压力（pin）设为0.5 Pa，开采压力（pout）设为0 Pa，模型长度（L）设为0.5 m，高度（h）设为0.1 m；多孔介质区域孔隙度设为0.2，渗透率设为1 000 mD。流体的密度设为1 kg/m3，黏度设为1 Pa·s，在交界面上BJS切向阻力系数（β）设为1.0。图2-b为注入端速度分布结果，表明数值解与解析解[49]基本一致，验证了渗流—自由流耦合模型的正确性。

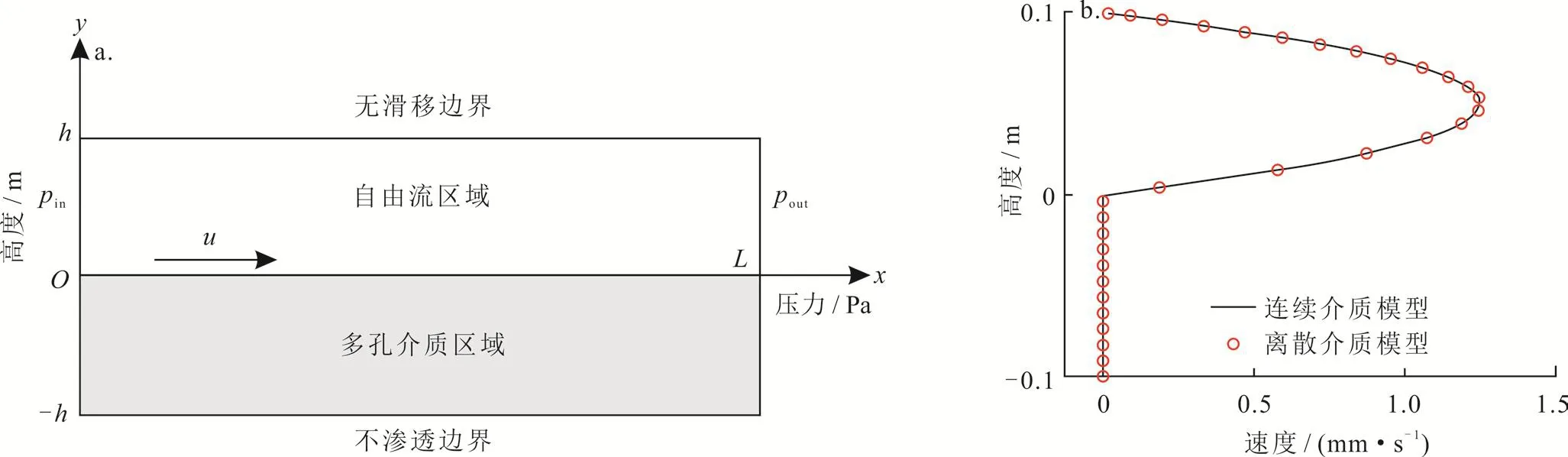
图2 渗流—自由流耦合模型及注入段速度分布对比图

1.2.4 热流耦合模型验证

通过与等效介质方法模拟缝洞介质热流耦合过程的结果对比，验证该研究中离散缝洞方法的准确性。如图3-a所示，模型大小为1 m×1 m，多孔介质为均质，直径0.2 m的溶洞及开度为0.15 mm的贯穿裂缝位于模型中心。缝洞介质初始饱和水，初始温度和压力分别为200 ℃和0 MPa。模型上下边界为不渗透绝热边界，模型左右侧为注入端和采出端，压力分别为pin= 0.2 MPa和pout= 0 MPa，注入温度为Tin= 60 ℃。详细的模型参数如下：基质孔隙度0.05，基质渗透率为1 mD，裂缝渗透率为1 000 mD，流体的密度为1 000 kg/m3，黏度为0.001 Pa·s，流体导热系数为 0.5 W/(m·K)，流体比热容为4 200 J/(kg·K－1)，基质的密度为2 600 kg/m3，基质导热系数为3.0 W/(m·K)，基质比热容为 1 000 J/(kg·K－1)，基质储水系数为1×10－9Pa－1，裂缝内储水系数为1×10－10Pa－1，在交界面上BJS切向阻力系数（β）为1.0，对流换热系数为3 000 W/(m2·K)。对于连续介质模型，裂缝显式表征为2维薄单元层（图3-b）；对于离散介质模型，裂缝表征为1维线单元（图3-b）。

图3 热流耦合模型设置及模型网格剖分图

图4给出了缝洞介质在热采1天后，缝洞介质内流速分布、流体压力分布及温度分布情况，结果表明基于连续介质模型和离散介质模型的结果基本一致。另外，图5给出了沿中间横轴缝洞介质内流速分布、沿中间纵轴缝洞介质内流速分布及出口平均温度随时间变化情况，可以发现裂缝内的流速远高于溶洞和基质内流速，而溶洞内流速远高于基质内流速，因此，与裂缝型介质类似，缝洞型介质中裂缝也是流体高速流动的主要通道。离散介质模型结果与连续介质模型结果的一致性，验证了该研究中缝洞介质热流耦合数值模型的准确性。

图4 热采1天后的流速、压力、温度分布图

图5 热流耦合数值模拟的流速、温度变化图

2 模型设置与结果分析

2.1 模型设置

该研究基于长为L=100 m的正方形区域（水平面），建立了一系列2维随机缝洞网络。为分析缝洞尺寸分布的影响，假设缝洞位置和走向是随机分布的。首先基于缝洞几何统计信息，建立裂缝网络和溶洞网络，然后对二者进行叠加，生成离散缝洞网络。裂缝长度（lf）服从幂律分布，上限和下限分别设置为lf,max=50L和lf,min=L/50。研究了3种裂缝长度指数情况：af=1.5、2.5和 3.5；3种裂缝密度情况：γf=0.2 m－1、0.4 m－1和 0.6 m－1；针对每一种裂缝参数组合下的裂缝网络，计算了相应的裂缝网络连通参数（pf）。溶洞直径上限和下限分别设置为lc,max=L/5和lc,min=L/25。因为溶洞尺寸幂律指数变化范围比较小（2.2～2.6），所以我们只考虑了溶洞尺寸指数ac=2.4的情况。该研究中溶洞孔隙度为φc=0.2。生成的裂缝网络涵盖了pf低于、接近和高于连通阈值（pfc）的情况，也就是存在不连通、处于过渡阶段和连通的裂缝网络。当af较大（如af=3.5）时，系统由小裂缝（lf＜L）控制；当af较小（如af=1.5）时，系统受大裂缝（lf与模型尺寸L相当）控制；当af=2.5时，系统受大裂缝和小裂缝同时控制。

缝洞型介质热流耦合模拟参数已在1.2.4节描述，其储层埋深为2 500 m，初始储层为饱和水状态，初始压力为25 MPa。基于水平对井（即1口注入水平井和1口开采水平井）进行开采，左侧注入井和右侧开采井的压力分别为27.5 MPa和25 MPa，保证流体在储层中的循环流动。储层初始温度为100 ℃，注入边界流体注入温度为30 ℃。流动和传热边界条件设置如图3-a所示。

2.2 结果分析

2.2.1 流动过程

为了研究缝洞型热储内流体流动特征，本文对比分析了不同缝洞网络参数（即af、γf、pf和φc）下，离散裂缝网络和离散缝洞网络的流速分布（图6）以及等效渗透率变化情况（图7）。为了方便对比和分析流体在具有相同裂缝几何参数下的裂缝网络和缝洞网络内的流动，基于裂缝网络内平均流速，对相应的裂缝网络和缝洞网络内的裂缝流速进行无量纲化（图6）。

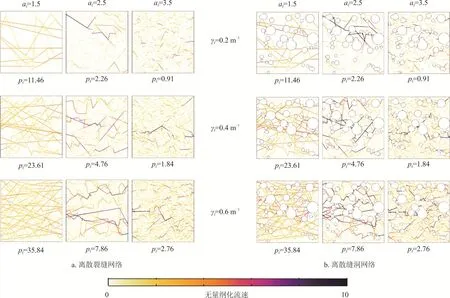
图6 离散裂缝与离散缝洞网络无量纲化流速分布图

针对裂缝网络内流体流动情况，如图6、7所示，①对于af=3.5的裂缝网络，流速相对较高的流动通道并不能贯穿注采两端，所以流体只能通过低渗基质和不连通的裂缝网络流动到出口端，系统的等效渗透率低；②对于af=1.5的裂缝网络，注采两端出现多条连通的高速流动通道，系统的等效渗透率高；③对于af=2.5的裂缝网络，当裂缝密度较低时（如γf=0.2 m－1、0.4 m－1），系统内不存在贯穿注采端的高速流动通道，系统等效渗透率较低；而当裂缝密度增大时，如γf=0.6 m－1，系统内出现几条贯通的高速流动通道，系统等效渗透率较高。

针对存在溶洞、缝洞网络内流体流动情况时，我们发现溶洞对流体流动起重要作用，主要分为两种作用：①溶洞的存在可以增多系统内贯穿注采端的高速流通通道或者使系统从不连通状态变为连通状态，例如，与af=2.5，γf=0.2 m－1的裂缝网络相比（图 6-a），由于溶洞的存在，系统从不连通状态转变为连通状态，也就是相应的缝洞网络内存在贯穿注采端的高速流动通道（图6-b），系统的等效渗透率增大了将近5倍（图7）；②溶洞的存在可以增大系统内与溶洞相连接的裂缝上的流速，相比于对应的离散裂缝网络，造成系统的等效渗透率出现增大的情况（图7）。

如图7-a所示，系统连通参数（pf）对等效渗透率（keq）起控制作用，具体表现为keq随pf的增加而增大。当pf＜pfc时，keq较低，这是因为系统内不存在贯通的高速流动通道，流体流动主要受低渗的基质控制。当pf＞pfc时，keq较高，这是因为系统内存在大量的贯通的高速流动通道，流体流动阻力低；当pf≈pfc时，keq出现突然增大，这是因为系统在该区域从不连通状态变为了连通状态，流动阻力显著降低。另外，我们发现，溶洞的存在会增大系统的等效渗透率，特别是当系统处于连通阈值（pfc）附近时，系统等效渗透率出现显著增大（图7-b）。这是因为在pfc附近，系统由于溶洞的存在从不连通变为连通的概率大。

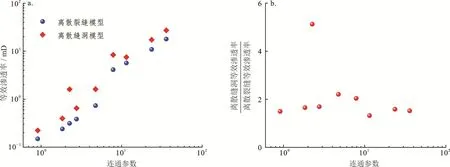
图7 离散缝洞与离散裂缝模型的等效渗透率及比值随连通参数变化图

2.2.2 传热过程

为了研究缝洞型热储内传热特征，笔者对比分析了不同缝洞网络参数（即af、γf、pf和φc）下，离散裂缝网络和离散缝洞网络的温度分布（图8），以及热采效率评价指标变化情况（图9）。

图8 热采1 800天后离散裂缝网络及离散缝洞网络内温度分布图

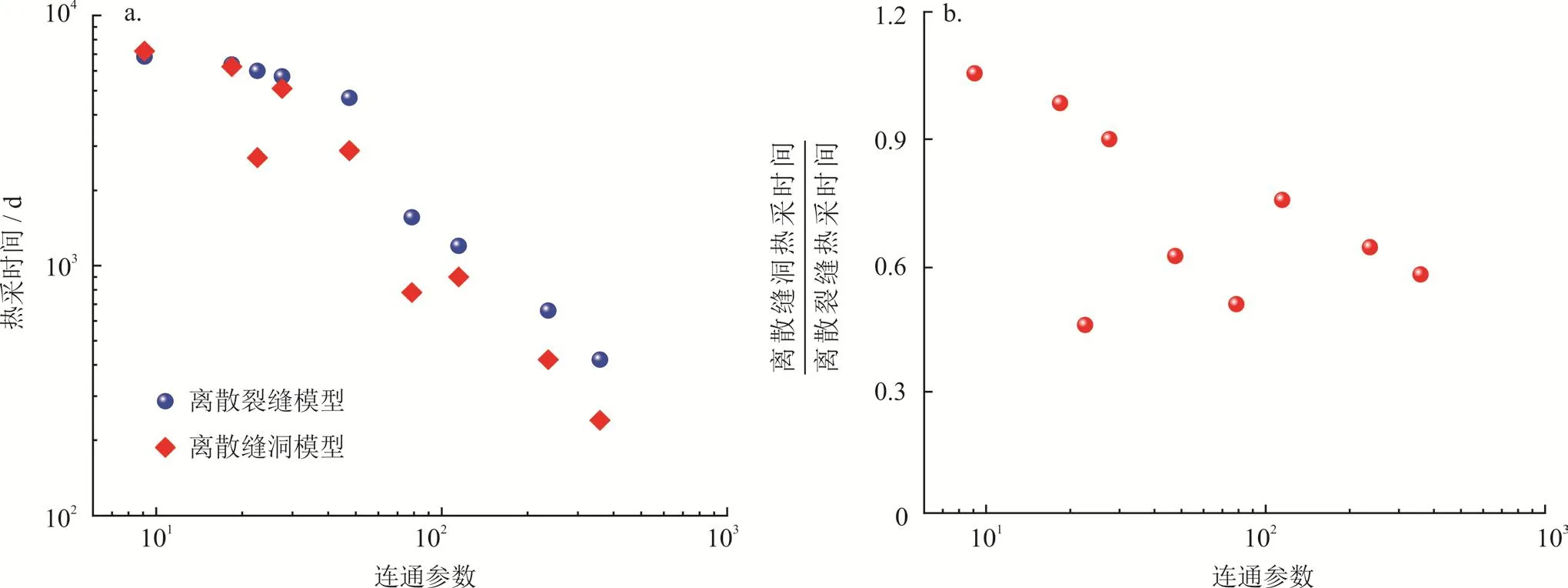
图9 整体热采率为30%时对应的热采时间及其热采时间比值随连通参数变化图

结合图6-a、8-a分析裂缝网络内流体流动下的传热情况，①对于af=3.5的裂缝网络，冷却前沿推进较慢，温度分布较均匀；这是因为系统内不存在贯穿注采端的高速流动通道，流体流动速度较低，换热过程由传热效率低的热传导方式控制。②对于af=1.5的裂缝网络，冷却前缘推进较快，冷流体波及面积较大，且温度分布呈现不均匀状态；这是因为系统内存在贯通的高速流通通道，换热过程由传热效率高的热对流方式控制。③对于af=2.5的裂缝网络，当裂缝密度较低时（如γf=0.2 m－1、0.4 m－1），与af=3.5的裂缝网络内的温度分布特征一致；而当裂缝密度增大时（如γf=0.6 m－1），存在较明显的冷却前缘锥进现象；这是因为系统内仅存在少数几条贯通的高速流动通道。

而针对存在溶洞、缝洞网络内传热情况时（图6-b、8-b），①发现对于af=3.5的裂缝网络，溶洞的存在对热储传热过程的影响较小，主要是因为溶洞的存在只能改变局部流体流动速度，而不能在系统内形成贯通注采端的高速流动通道，换热过程主要还是由热传导控制。②对于af=1.5的裂缝网络，溶洞的存在使冷却前缘推进加速，冷流体波及面积更大；这是因为溶洞的存在使系统内流体流速加快，热对流过程增强。③对于af=2.5的裂缝网络，当裂缝密度较大时（如γf=0.6 m－1），溶洞对系统传热的作用与对af=1.5的裂缝网络的传热作用一致；而当裂缝密度较低时（如γf=0.2 m－1、0.4 m－1），从均匀的冷却前缘变化为明显的锥进的冷却前缘，冷流体波及面积增大；这是因为溶洞的存在使系统从不连通状态变化为连通状态，系统换热过程从效率低的热传导过程变为效率高的热对流过程。

为了研究热储的换热效率，定义了热采效率评价指标：热储整体热采率达到裂缝型热储可采热量的30%，所对应的热采时间（即tγglobal=30%）根据式（20）计算得到。热采时间越短，表明在开采相同的热储能量情况下，热采速度和热采效率更高。如图9所示，系统连通参数（pf）对热采时间（即热采效率）tγglobal起控制作用，具体表现为tγglobal随pf的增加而降低。当pf＜pfc时，热采时间长，热采效率低；这是因为系统的传热主要受热传导控制，导致换热效率较低。当pf＞pfc时，热采时间短，热采效率较高；这是因为系统内流动速度较大，传热过程主要受换热效率高的热对流方式控制。另外，我们发现，相比于裂缝网络，溶洞的存在会增大系统的热采效率，并且整体上，随着pf的增大，溶洞对系统热采效率的提高作用越大。特别地，当系统处于pfc附近时，由于溶洞的存在，系统的热采效率出现显著增大。

3 结论

1）针对缝洞型岩溶热储的多尺度、强非均质和多流态的特点，提出了基于离散缝洞网络方法的热流耦合数值模型，其中多孔介质渗流区采用达西定律描述、溶洞自由流区域采用N—S方程描述，两区域间采用BJS边界条件进行耦合，并基于局部非热平衡理论，描述冷流体与热基岩在缝洞界面上的热量交换。通过与解析解和连续介质模型解对比，验证了离散缝洞热流耦合模型的准确性。

2）裂缝网络连通性是控制和评价缝洞型热储流动传热效果的关键参数，而溶洞的存在对热储内的流动传热效果起重要影响。对于连通性较差的系统，流体流动速度小、等效渗透率低，热采效果差；对于连通性好的系统，流体流动速度大、等效渗透率高，热采效果好。溶洞主要通过两个作用影响热储内的流体流动和传热：一是溶洞的存在会增加系统内贯穿的高速流动通道数量，甚至使系统从不连通变为连通；二是溶洞的存在会增大系统内局部流动通道速度。因此，对于基质渗透率较低，不存在连通或连通性较差的热储，能够基于裂缝网络连通性指标，指导缝洞型碳酸盐岩热储进行酸化或者压裂，形成具有开发价值的人工热储。另外，在酸化或压裂造缝过程中，尽量使改造裂缝与溶洞相交，提高热采效率。