混沌脉宽调制电场激励油中液滴振动动力学特性分析
2022-05-11张又于龚海峰廖治祥
彭 烨, 张又于, 龚海峰,2, 廖治祥, 邱 值, 余 保
(1.重庆工商大学 制造装备机构设计与控制重庆市重点实验室,重庆 400067;2.重庆工商大学 废油资源化技术与装备教育部工程研究中心,重庆 400067;3.中国石油大学(华东) 重质油国家重点实验室,山东 青岛 266580)
电场破乳脱水被广泛应用于石油开采、废油资源化等领域,具有清洁、高效和节能的优点[1-3]。在电场破乳工艺中,常见的电场形式可分为:交流电场法、直流电场法、交直流双电场法、脉冲电场法[4-6]。比较而言,脉冲电场破乳能更加有效激励油中液滴振动和碰撞,提高聚结效率,具有更好的破乳效果[7]。研究表明,脉冲电场破乳关键因素是乳化油中液滴在电场激励下产生共振现象,剧烈振动变形为相邻液滴碰撞聚结提供了动能,并减小了油/水界面膜的强度,实现了油中液滴的快速聚结,存在最佳电场频率,策动油中液滴发生共振,使液滴聚结更为高效[7-10]。
然而,油包水(W/O)型乳化油中液滴粒径分布范围广,小至微米级,大至毫米级,且在破乳过程中不断发生聚结与破碎[11]。显然,恒定频率脉冲电场不能覆盖油中所有液滴的共振频率,未能完全发挥脉冲电场法的破乳效果。景微娜等[12]首次将混沌信号引入脉冲电场脱水,提出应用具有混沌特性的脉冲电场实现W/O型乳化油的最佳共振脱水,并通过仿真获得了液滴在混沌电场中的状态,结果表明液滴的振动响应具有混沌特性。但其研究属于初步探索阶段,混沌电脱水的破乳机理和液滴的变形机制尚不明确。Peng等[11]通过手动调节脉冲电场频率以应对破乳过程中液滴粒径动态分布导致的最佳共振频率变化,结果表明变频脉冲电场能有效改善液滴的聚结效率,但是手动调节操作性差,难以满足工业需求。龚海峰等[13]在前期研究中采用定幅值、等脉宽的混沌频率脉冲电场激励油中液滴振动,以期应对最佳破乳频率的动态变化,结果表明混沌频率电场能有效覆盖油中所有液滴的共振频率,且液滴在电场中的振动为混沌振动。然而,不同粒径液滴达到共振所需的脉冲宽度不同,故使用等脉宽的混沌电场不能使油中所有液滴达到理想的共振状态。
此外,占空比(脉冲电场高电平时间与整个脉冲周期的比值)是脉冲电场破乳方法的一个重要参数,恰当的占空比可以保证液滴在脉冲持续时间内的变形达到最大,并且在休止期内水链能够及时消散。Bailes等[14]认为脉冲施加时间等于休止时间时,聚并效果最好。在后续的研究中,学者们大多都采用占空比为0.5的脉冲电场。梁雯[15]发现,对于不同含水率的乳状液,低占空比可有效防止高含水率乳状液液滴成链;而对于低含水率乳状液来说,提高占空比可进一步改善脱水效果。孙治谦等[16]在理论分析基础上进行显微实验,得出随占空比的增加,作用于水滴的电场能随之增加,水滴变形度增加;占空比过大,部分电场能经油相发生泄漏,水滴变形度小幅降低。
鉴于此,笔者提出一种混沌脉宽调制电场破乳方法,即应用定幅值、等占空比、脉宽混沌的脉冲电场实现乳化油液滴的高效聚结。通过建立液滴混沌脉宽调制电场振动模型,研究液滴在混沌脉宽调制电场中的变形动力学行为与混沌特性,为混沌脉冲电场破乳方法提供理论依据。
1 液滴混沌脉宽调制电场振动模型
1.1 混沌脉宽调制电场
混沌脉宽调制电场具有占空比恒定、脉冲宽度混沌变化的特点,可满足乳化油中绝大部分液滴共振频率。由于目前尚无能够实现占空比恒定、电场频率混沌变化的混沌脉宽调制的方法,故采用Logistic满映射[17]构造一维混沌序列,将该序列映射到电场频率中,使得电场频率混沌,而占空比保持恒定,从而实现混沌脉宽的调制。其电场信号调制原理如图1所示。
令电场强度为E,占空比为d,使脉冲频率ωi在[ωl,ωn]范围内混沌。ωi的公式如式(1)所示。
(1)
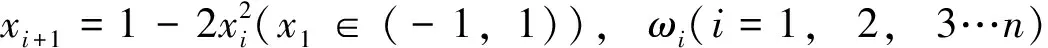
调制的脉宽τi如式(2)所示。
(2)
式中,τi(i=1, 2, 3…n)为迭代i次的电场脉冲宽度,从而得到混沌脉宽调制电场E(t)表达式如式(3)所示。
(3)
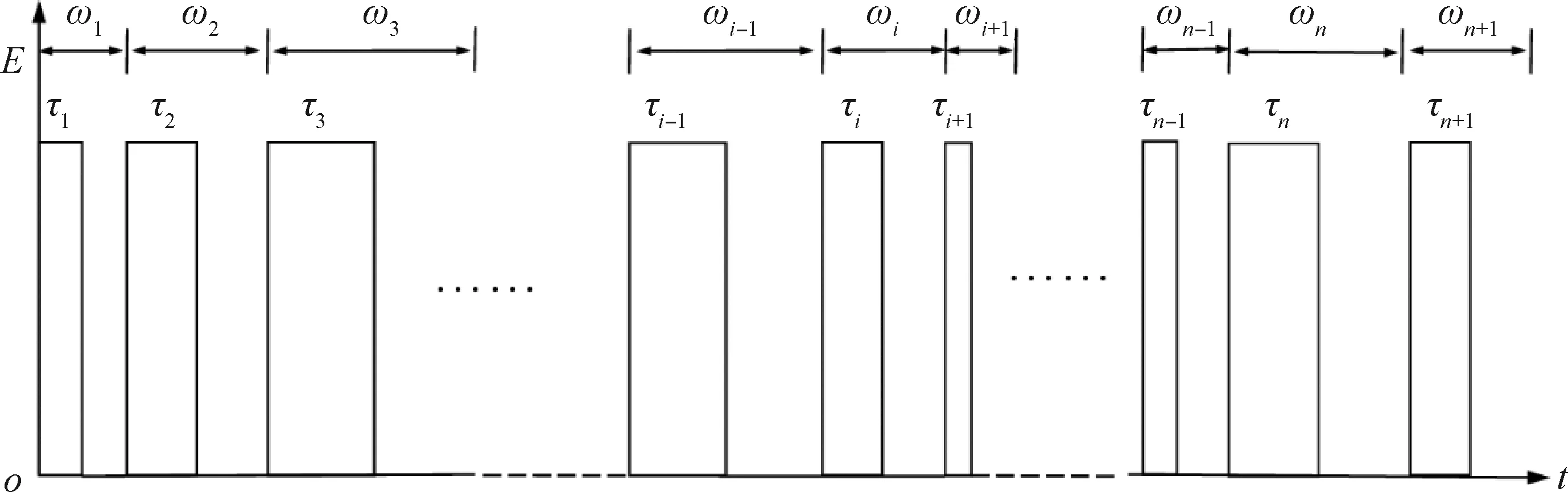
ωi(i=1,2,3……n)—Electric field pulse angular frequency of the nth iteration;τi(i=1,2,3……n)—Electric field width of the nth iteration图1 混沌脉宽调制电场信号Fig.1 The signal of chaos pulse width modulation electric field
1.2 液滴振动动力学模型
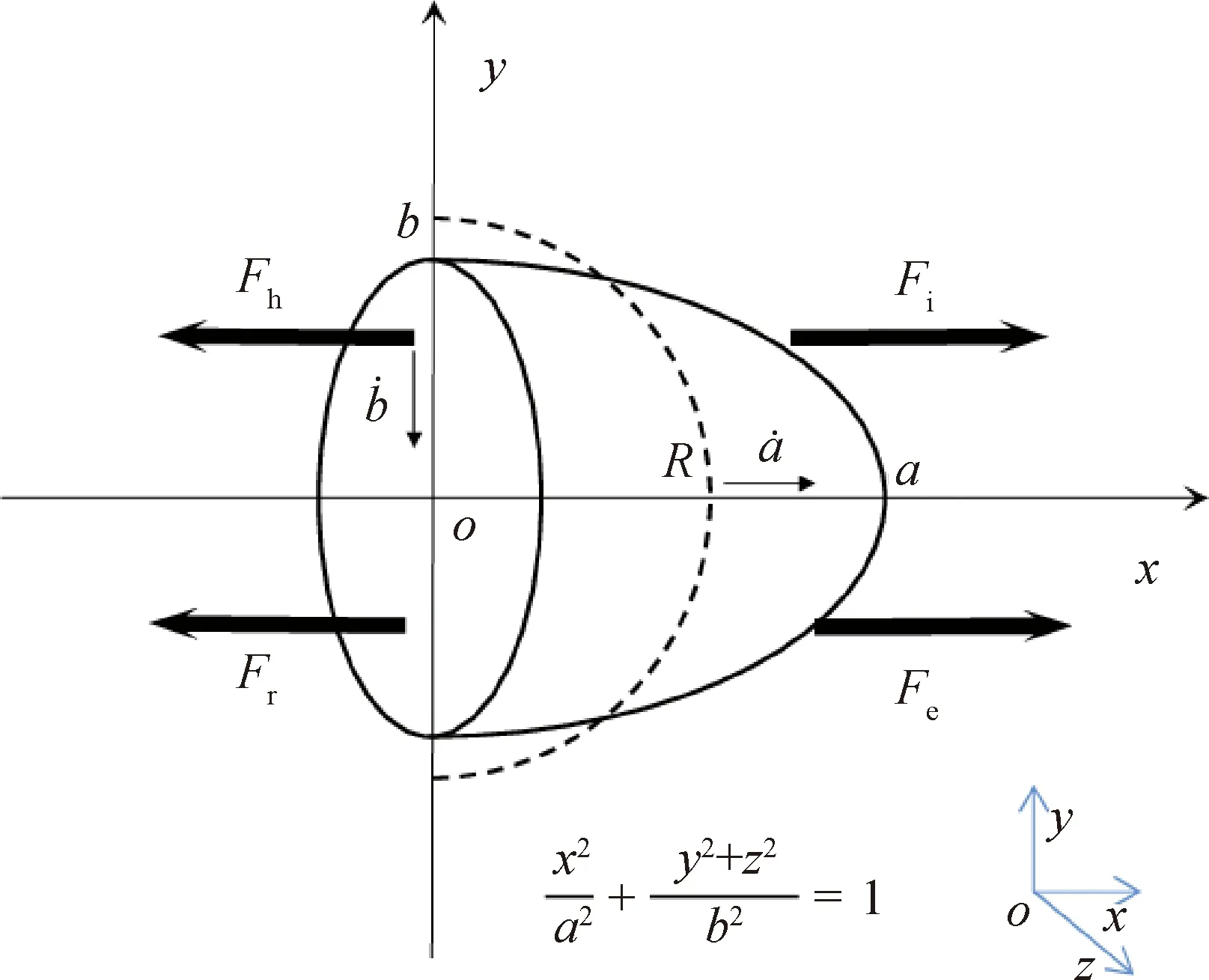
a—Long half axis of droplet; b—Short half axis of droplet; half-axis deformation velocity of droplet; half-axis deformation velocity of droplet;Fe—Electric field excitation of droplet vibration;Fr—Oil resistance of droplet vibration;Fi—Inertia force of droplet vibration;Fh—Restoring force of droplet vibration图2 液滴右半球受力示意图Fig.2 The force diagram of the righthemisphere of the droplet
油中的液滴在电场中主要受4个力的作用[19-20]:电场激励液滴振动的激励力Fe、油液阻力Fr、液滴惯性力Fi和振动恢复力Fh。根据平衡条件得到:
Fr+Fi+Fh=Fe
(4)
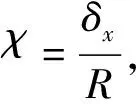
(5)
其中:
(6)
(7)
(8)
(9)
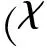
2 数值计算
2.1 计算初始条件
为了便于分析液滴在混沌脉宽调制电场中的振动变形规律,采用不同粒径的液滴作为考察对象。设油中含有半径(R)为0.4、0.6、0.8、1.0、1.2、1.4 mm的液滴,液滴密度ρw(20 ℃)为1×103kg/m3,油的黏度μo(20 ℃)为47.2 mPa·s,相对介电常数ε2为 5,油/水界面张力γ为12 mN/m,所施加的混沌脉宽调制电场强度E为3×105V/m。当电场频率和液滴共振频率相接近时,液滴出现共振,电场破乳效果较好[21]。求解液滴非线性振动动力学模型[20]得到不同粒径液滴在脉冲电场中的幅频特性曲线如图3所示。
混沌频率的上下限可通过液滴的共振频率范围确定,从而取混沌脉宽调制电场频率上限为610 rad/s,下限为70 rad/s,即脉宽上限为0.0449 s,下限为0.0052 s,令混沌初值x1为0.2,占空比d为0.5。由式(1)~式(3)求出混沌脉宽调制电场脉冲信号,如图4所示。
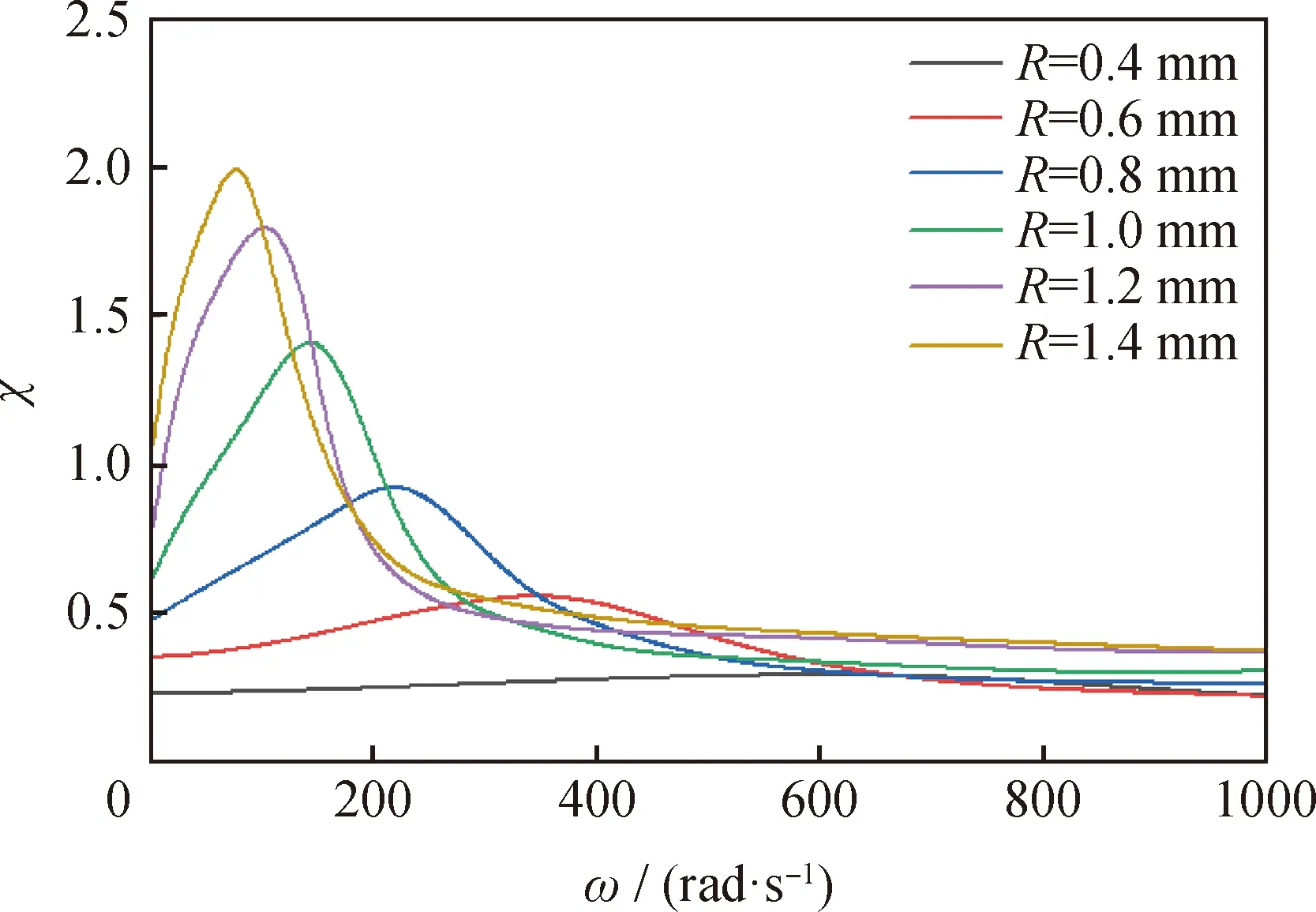
—The amptitude of droplet; ω—The angular of electric field图3 液滴幅频特性曲线Fig.3 Amplitude frequency characteristic curve of dropletsε2=5; γ=12 mN/m; E=3×105 V/m
由图4可以看出,电场脉冲信号的幅值保持一定,占空比恒为0.5,脉冲宽度随时间不断迭代变化,使得脉冲电场的角频率在0~1 s内在77~603 rad/s之间混沌变化。取液滴在混沌脉宽调制电场中的初始振动速度为0,初始振幅为0.0001。计算起始时间为0,结束时间为1 s,采用自适应步长Runge-Kutta算法ode45对模型进行求解。
2.2 模型验证
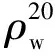
由图5可知,液滴振幅的数值结果略低于实验结果。这是因为液滴振幅的数值结果是在理想的条件下得出的,而实验会受外界的干扰以及测量误差的影响,同时由于计算精度的影响,液滴振幅的数值结果也存在一定的误差,故模型计算得到的液滴变形量相较而言低于实验结果,但两者趋势具有很好的一致性,说明液滴振幅的数值结果可以较为准确地预测油中液滴的变形情况,即此模型能够合理地预测液滴在混沌脉宽调制电场中的振动。
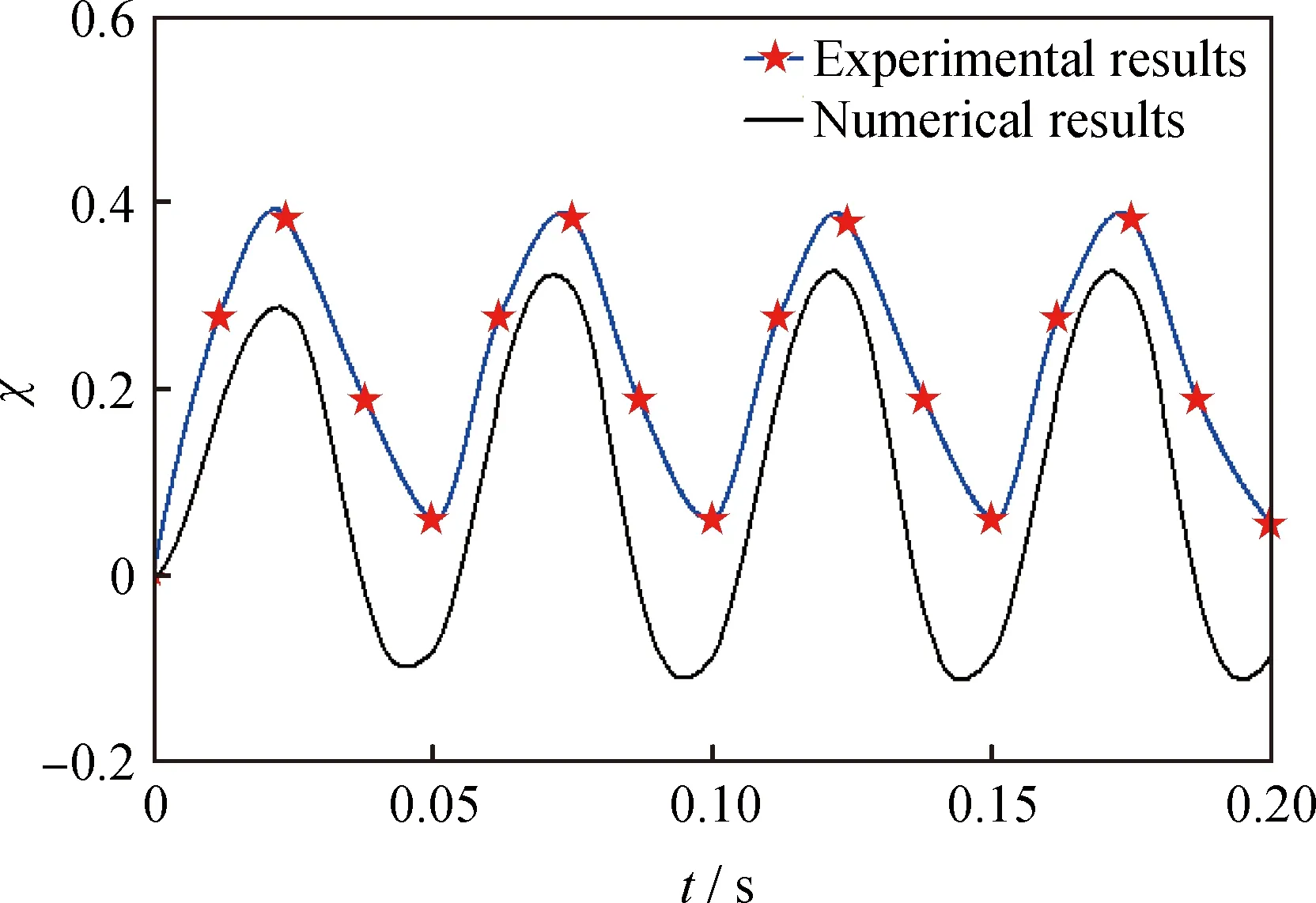
—The amptitude of droplet; t—Time图5 液滴变形数值结果与实验结果[20]对比Fig.5 Comparison of numerical and experimental results[20]of droplet deformationConditions: =998 kg/m3; =60.3 mPa·s;ε2=4.6; γ=19 mN/m; E=2×105 V/m
3 结果与讨论
3.1 单个液滴响应特性
取半径R为0.6 mm的单液滴,计算得到该液滴在混沌脉宽调制电场中的振动响应结果如图6所示。
由图6可知,液滴在混沌脉宽调制电场作用下存在共振,其振幅不超过共振幅值,液滴在电场中表现为在高频区域振动频率较高,振幅较低,在电场低频区域振动频率较低,振幅较高。由于液滴在电场高频区域,脉宽较小,液滴所受的电场激励时间较短,液滴被极化拉伸的程度不足,故振幅较低;在低频区域,脉宽较大,液滴受到电场激励时间较长,液滴被充分拉伸,振幅较大。为探究液滴在混沌脉宽调制电场中的振动变形机制,对液滴在0 s至0.3 s的振动变化情况进行深入分析,如图6(b)所示。当电场频率趋近于液滴共振频率(ω/ωr≈1)时,液滴振幅趋近于共振幅值;当电场频率与液滴共振频率的比值大于0.5(ω/ωr>0.5)时,液滴的振动频率与电场频率一致;而当电场频率与液滴共振频率的比值小于0.5(ω/ωr<0.5)时,液滴的振动频率高于电场频率,在高电平内持续振动,且振幅出现衰减。这是由于当ω/ωr≈1时,液滴发生共振,故振幅趋近于共振幅值;而当ω/ωr>0.5时,电场作用时间相对较短,液滴所受到的电场激励力大于振动恢复力和油液阻力,液滴持续拉伸,当失去电场后,液滴失去电场激励力的作用,振动恢复力克服油液阻力而收缩,这种伸缩振动周期同步于电场脉冲周期,故其振动频率与电场频率一致;当ω/ωr<0.5时,电场频率较低,液滴受电场作用时间较长,被拉伸至最大振幅后继续受到电场激励力作用,由于电场激励力会随着振动幅值增大而减小,振动恢复力随着振动幅值增大而增大,液滴达到最大振幅时,油液阻力和液滴惯性力均为0,振动恢复力大于电场激励力使其收缩,液滴振动幅值减小,电场激励力再次大于振动恢复力和油液阻力使其拉伸,故液滴出现衰减振动。
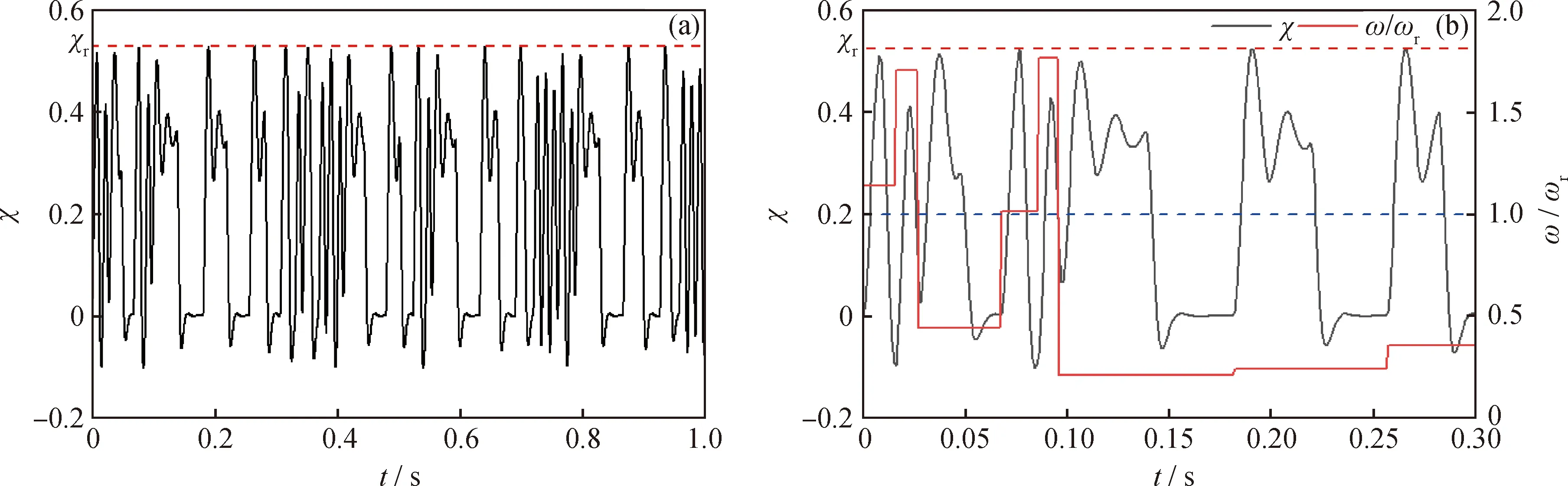
—The amplitude of droplet; t—Time;r—The resonance amplitude of the droplet;ω/ωr—The ratio of electric field frequency to droplet resonance frequency图6 单液滴振动响应曲线Fig.6 The vibration response curve of single droplet(a) 0—1 s; (b) 0—0.3 sConditions: =1×103 kg/m3; =47.2 mPa·s; ε2=5; γ=12 mN/m; E=3×105 V/m
3.2 不同液滴响应特性
取液滴半径R分别为0.4、0.6、0.8、1.0、1.2、1.4 mm,通过计算得到不同液滴在混沌脉宽调制电场中的响应结果,如图7所示。
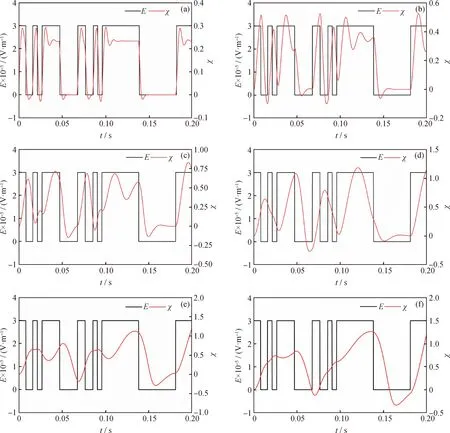
E—The strength of electric field;—The amplitude of droplet; t—Time图7 各液滴变形与电场信号对比图Fig.7 The comparision of droplets deformation and electric field signal(a) R=0.4 mm; (b) R=0.6 mm; (c) R=0.8 mm; (d) R=1.0 mm; (e) R=1.2 mm; (f) R=1.4 mmConditions: =1×103 kg/m3; =47.2 mPa·s; ε2=5; γ=12 mN/m
由图7可知,各液滴在混沌脉宽调制电场中的振动响应趋势存在明显差异,具体表现为液滴粒径越大,最大振幅越高,振动频率越低。当液滴半径小于0.8 mm时,其在混沌脉宽调制电场中存在局部高频振动;当半径大于0.8 mm时,液滴的局部高频振动现象不明显甚至消失。上述情况是由于对于半径较小(R≤0.8 mm) 的液滴,如3.1节所述,当电场频率较高时,液滴的振动频率与电场频率一致,由于混沌脉宽调制电场的脉冲频率存在局部高频区,故液滴的振动也存在局部高频现象;当液滴半径较大(R>0.8 mm)时,液滴的质量较大,其液滴惯性力也越大,当失去电场作用后,液滴会在液滴惯性力的作用下继续拉伸,而电场高频区的脉冲间隔较短,液滴尚未发生收缩并继续受到下一脉冲的作用,所以液滴的振动并未完全跟随电场频率,因此未出现明显的高频振动现象。深入分析不同液滴在电场中的振动响应特性,当液滴R=0.4 mm时,其在电场的每个脉冲均能达到最大振幅,但是当脉冲频率较低时,其振幅会在高电平先达到最大振幅,随后略微降低,最终趋于稳定;当R=0.8 mm时,在电场频率小于液滴共振频率的周期内,其振动存在明显的滞后现象,具体表现为液滴在电场低电平持续被拉伸,在高电平继续收缩;随着液滴粒径的增大,振动响应滞后现象更为突出,如R=1.0 mm至R=1.4 mm的响应结果所示,液滴在频率较高的低电平内不发生收缩且高电平内不被拉伸,从而振动周期变长。
造成上述现象的原因在于液滴的变形受电场频率和自身受力变化的影响。因为本研究的混沌脉宽调制电场的频率范围是根据不同粒径的共振频率确定的,R=0.4 mm的共振频率接近电场频率的上限,因而电场的脉冲宽度均大于液滴共振所需的脉宽,其在电场中的振动均能达到最大振幅,在脉冲频率较低时,高电平持续时间较长,液滴受力变化跟液滴的瞬时振幅相关,当液滴被拉伸到最大振幅之后,振动恢复力大于电场力而发生收缩,当收缩到一定程度后,振动恢复力小于电场激励力而被拉伸,振幅逐渐衰减,最终趋于稳定,此时电场激励力与振动恢复力相等,不再振动。随着液滴粒径增大,其质量逐渐增大,惯性力增大,当电场频率高于液滴共振频率时,液滴在高电平阶段受到电场激励力的作用被拉伸,当失去电场作用时,液滴受到的电场激励力突变为0,此时惯性力大于振动恢复力,液滴被继续拉伸,从而出现拉伸响应滞后现象;液滴在低电平阶段失去电场激励力作用,振动恢复力使其收缩,当在下一高电平受到电场激励力时,液滴的振动恢复力和惯性力大于电场激励力,液滴持续收缩,因此产生收缩滞后现象。
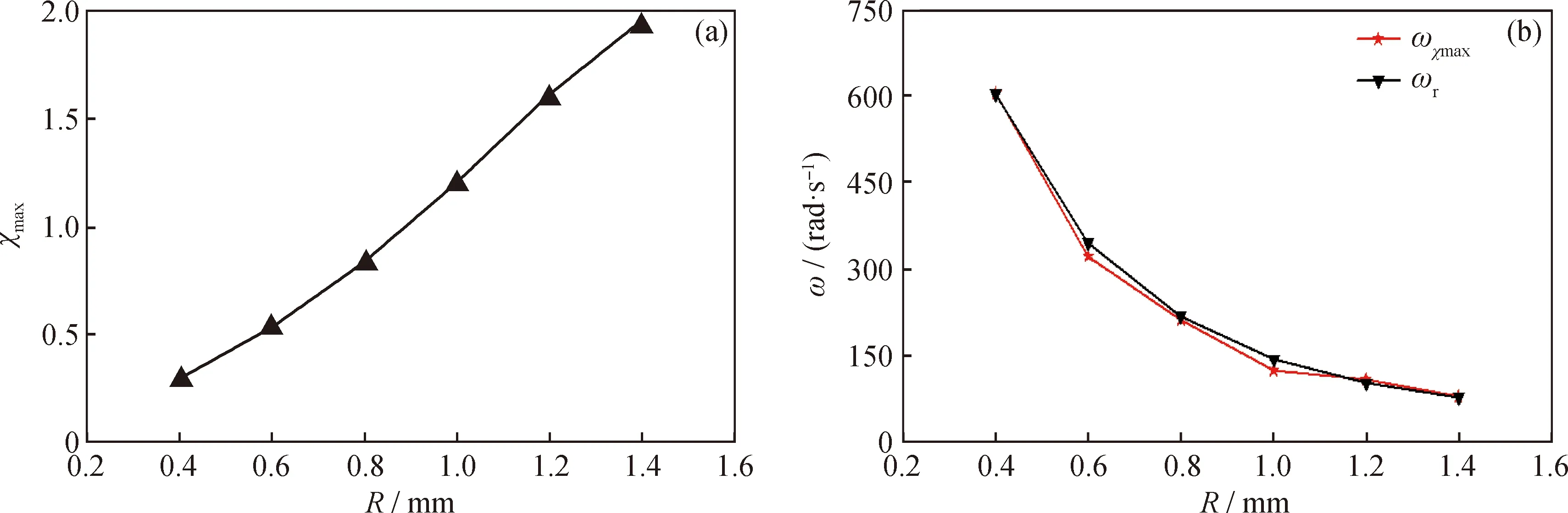
max—The droplet response amplitude; ω—The angular of electric field; R—Radius of spherical dropletsωχmax—Electric field frequency at maximum vibration amplitude of droplets; ωr—The resonance frequency of droplets图8 液滴的最大振幅与共振频率随粒径的变化Fig.8 Maximum amplitude and resonance frequency of droplet change with particle size(a) Maximum amplitude of droplet; (b) Contrast of frequencyConditions: =1×103 kg/m3; =47.2 mPa·s; ε2=5; γ=12 mN/m;E=3×105 V/m
由图8可得,液滴最大振幅随半径增大而增大,液滴达到最大振幅时的电场频率和液滴共振频率接近。这是由于随着液滴粒径的增大,其受到的电场激励力和惯性力增大的程度大于振动恢复力增大的程度,所以粒径越大的液滴更容易拉伸到较大振幅。电场频率的调制范围是根据液滴共振频率计算得出的,其频率在设定的最大粒径和最小粒径的共振频率之间混沌变化,在有限时间内,电场频率的迭代值并不完全趋近于所有液滴的共振频率,但是当电场频率接近液滴共振频率时,液滴能达到最大振幅。
3.3 液滴振动混沌特性
研究表明,通过引入混沌信号能使液滴的振动具有混沌特性[13]。液滴在混沌脉宽调制电场中振动的混沌特性可以通过Kolmogorov熵进行表征。在混沌系统中,Kolmogorov熵K表示系统不可预测性的程度,描述混沌轨道随时间演化信息的产生率[22]。当K=0时,系统运动是周期状态;K→∞时,系统运动是随机状态;K为一个确定的正值时,系统运动是混沌状态,且K越大,其混沌程度越大,运动越无序[23]。
可通过最大似然法估算Kolmogorov熵(KM)[24]。不同粒径液滴在混沌脉宽调制电场中振动时间序列的最大似然估计值KM的计算结果如图9所示。
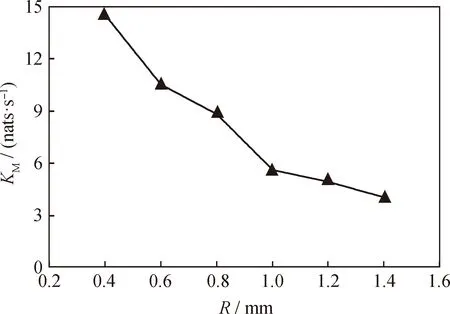
KM—Maximum likelihood estimation of kolmogorov entropy;R—radius of spherical droplets图9 不同粒径液滴振幅的Kolmogorov熵(KM)Fig.9 Kolmogorov entropy (KM) of droplet amplitudewith different particle sizesConditions: =1×103 kg/m3; =47.2 mPa·s;ε2=5; γ=12 mN/m; E=3×105 V/m
由图9可知,所有液滴振动响应的KM均大于0,随着液滴粒径的增大,其振动响应的KM逐渐减小。这说明液滴在混沌脉宽调制电场中的振动为混沌振动,且其混沌程度随液滴粒径的增大而减小。这是由于液滴振动是由电场激励产生的,电场脉宽的混沌导致了液滴振动的混沌,随着粒径的增大,液滴振动响应的滞后程度加深,导致液滴振动频率与电场频率的一致性降低,从而混沌程度减小。
4 结 论
建立了乳化液滴在混沌脉宽调制电场中的混沌振动动力学模型,通过对模型的数值计算和结果分析,得出以下结论:
(1)当电场频率与液滴共振频率的比值小于0.5时,液滴在电场高电平发生衰减振动,振动频率大于电场频率;当电场频率与液滴共振频率的比值大于0.5时,液滴振动频率与电场频率一致。
(2)液滴在电场中的响应存在滞后现象,且粒径越大,滞后现象越明显,导致液滴的振动频率不完全跟随电场频率。
(3)液滴最大振幅随半径增大而增大,达到最大振幅时的电场频率和液滴共振频率接近,即液滴在共振频率附近发生共振。
(4)液滴在混沌脉宽调制电场中振动时间序列的KM大于0,说明液滴的振动为混沌振动,且KM随粒径增大而减小,表明液滴振动的混沌程度随粒径的增大而降低。
符号说明:
a——液滴长半轴,m;

A,B,G——振动方程各受力项常数;
b——液滴短半轴,m;

d——混沌脉宽调制电场的占空比;
E——电场强度,V/m;
Fe——液滴振动受到的电场激励力,N;
Fr——液滴振动受到的油液阻力,N;
Fi——液滴振动惯性力,N;
Fh——液滴振动恢复力,N;
K——Kolmogorov熵,nats/s;
KM——Kolmogorov熵的最大似然估计值,nats/s;
R——液滴半径,mm;
t——时间,s;
γ——界面张力,N/m;
δx——液滴长半轴伸长量,m;
ε0——真空介电常数;
ε2——油液相对介电常数;
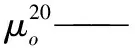
τi——第i(i=1,2,3…n)次迭代的电场脉宽,s;
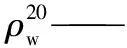
xi——Logistic满映射第i(i=1,2,3…n)次混沌迭代值;
χ——液滴振幅;
χr——液滴共振幅值;
χmax——液滴最大振幅;
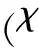
ωl——电场角频率下限,rad/s;
ωn——电场角频率上限,rad/s;
ωi——第i(i=1,2,3…n)次迭代的电场角频率,rad/s;
ωr——液滴共振角频率, rad/s;
ωχmax——液滴最大振幅下的电场角频率,rad/s。
