基于BP神经网络的单人步行荷载参数识别
2022-05-11浦炜钦宋志刚胡一鸣张博皓
浦炜钦,宋志刚,胡一鸣,张博皓
(昆明理工大学建筑工程学院,云南昆明 650500)
引言
步行荷载是人致结构振动的重要研究内容,大部分荷载模型将步行荷载视为每一步完全相同的周期性荷载。试验研究表明,步行荷载是一个复杂的窄带随机过程[1],同时,行人左右脚的步行荷载存在差异,导致步行荷载并非真正的周期性荷载,在步行荷载频谱的主谐波附近存在能量泄漏[2],所以在识别和重构步行荷载时应当考虑亚谐分量的影响。
在步行荷载傅里叶级数模型中,步频、各阶动载因子与相位角是构造步行荷载时程的主要参数。目前关于相位角的研究较少,Ellis等[3]的研究表明,相位角具有随机性,实践中可用平均值来表示步行荷载的相位角;Zavanovic等[4]与操礼林[5]认为各阶分量的相位角在[-π,π]上相互独立并服从均匀分布;陈隽等[6]给出了相位角的具体取值,在随后的研究中经过大量数据分析得出相位角服从正态分布[7]。多数研究忽略了亚谐分量的相位角,不同学者得到的相位角分布情况也具有较大差异,而且由于相位角随机性的影响,将其取平均值或是某一确定值并不能很好地反映步行荷载的随机特征。
针对上述问题,文中通过无线传感技术获得步行荷载加速度时程,基于包含亚谐分量的傅里叶级数模型[8],提出均匀试验设计与BP神经网络相结合的参数识别方法,对比分析实测-重构步行荷载时程,验证了该方法的准确性。
1 试验设计
1.1 试验原理
步行荷载可分为竖向、纵向和横向3个方向的荷载分量,其中竖向步行荷载分量可表示为:

式中:F(t)为竖向步行荷载分量时程函数;m为人体质量;g为重力加速度;a()t为步行荷载竖向的质心加速度时程函数。由式(1)可知,可通过测量人体竖向质心加速度间接获得竖向步行荷载分量。已有研究表明,腰部是最接近人体质量中心的位置,且受到的振动干扰较小,质心加速度输出信号比较平缓,通过质心加速度间接获得的步行荷载及其动载因子与已有测力板试验值基本一致[9],文中以竖向分量步行荷载为研究对象,设计以下试验方案。
1.2 试验方案
使用采样频率为100 Hz的无线传感器进行试验,通过测定人体质心加速度间接获得步行荷载。考虑到行人正常行走的步频范围,选择测试步频为1.6、1.8、2.0、2.2、2.4 Hz,每个步频进行30组试验,截取10 s的稳定数据进行分析,限于篇幅,仅给出步频为1.8 Hz与2.4 Hz的实测步行荷载加速度时程,如图1所示。可以看出,相比步频为1.8 Hz的实测步行荷载,步频为2.4 Hz的实测步行荷载周期性较弱,测试者左右脚的荷载差异明显。

图1 实测质心加速度时程Fig.1 The measured body mass center acceleration time history
2 识别算法
2.1 荷载模型
通常考虑步行荷载的前五阶分量,将连续步行荷载近似为一个由不同频率简谐激励组成的傅里叶级数表达式,见式(2):

式中:F(t)为步行荷载时程函数;DLFi、φi分别为第i阶主谐分量的动载因子和相位角;G、fs和t分别为行人静止重力、步频和步行时间。
式(2)仅包含主谐分量的动载因子和相位角,不能体现步行荷载的非周期性,所以基于式(1)引入亚谐分量式(3),得到包含亚谐分量的傅里叶级数模型[8],见式(4):

其中fz(t)如式(5)所示:
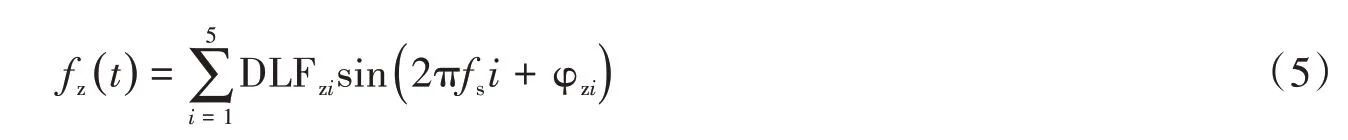
式中:fz(t)、fy(t)分别为主谐分量和亚谐分量;DLFzi、φzi分别为主谐分量的第i阶动载因子和相位角;DLFyj、φyj分别为亚谐分量的第j阶动载因子和相位角。为便于区分,将式(2)记为模型Ⅰ,式(4)记为模型Ⅱ。
由式(2)~式(5)可知,重构步行荷载需要识别步频和主、亚谐分量的前五阶动载因子及相位角,因此设计以下识别方法。
2.2 动载因子识别
将实测步行荷载时程进行傅里叶变换得到荷载频谱,限于篇幅,仅给出步频为1.8 Hz与2.4 Hz的实测步行荷载频谱和动载因子,如图2、表1所示。主谐波峰值出现的频率即为实际步频fs,步频及其整数倍频处的幅值即为主谐分量的动载因子,在0.5fs、1.5fs、2.5fs、3.5fs、4.5fs附近存在各阶亚谐波,其幅值即为亚谐分量的动载因子,将部分主、亚谐分量动载因子统计如表1所示。可以看出,步频为1.8 Hz的实测步行荷载亚谐波较弱,步频为2.4 Hz的实测步行荷载亚谐波较强,这说明亚谐波随着步行荷载非周期性的提高而增强。

图2 实测步行荷载频谱Fig.2 The measured walking load spectrum
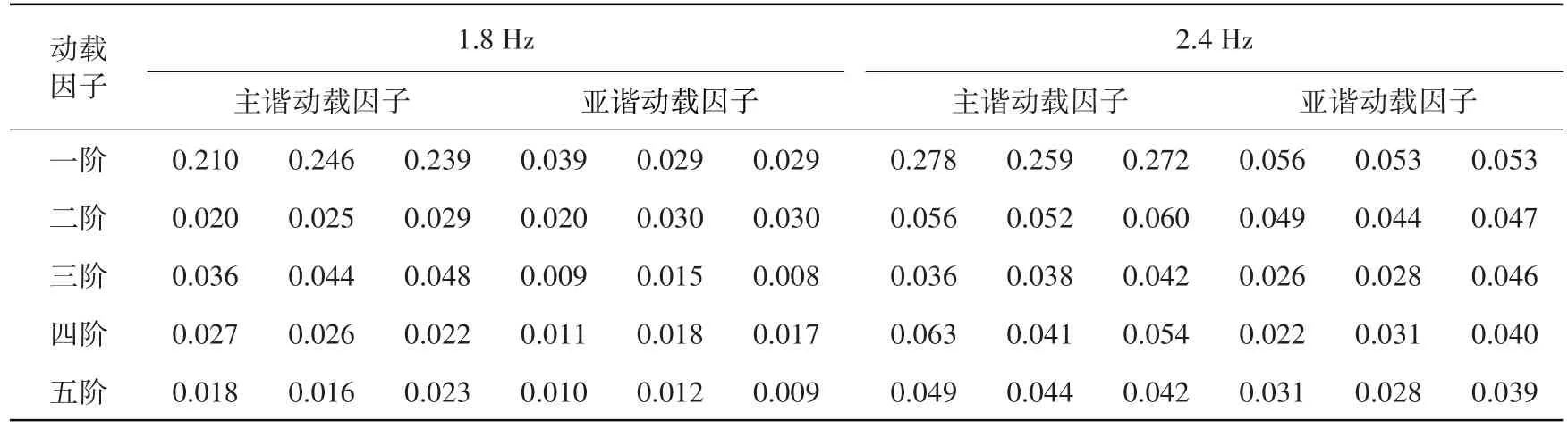
表1 动载因子统计Table 1 Dynamic load factor statistics
2.3 相位角识别
2.3.1 均匀试验设计
均匀试验设计表是一个n行m列的矩阵,当试验因素数即列数m较多时,可由方幂法构造均匀表。由式(2)~式(5)可知,在已知测试者体重并统计得到实际步频和动载因子的基础上,还需对相位角进行识别。模型Ⅰ中,因素数m=5,即主谐分量前五阶相位角;模型Ⅱ中,因素数m=10,即主、亚谐分量的前五阶相位角。均匀设计表第k个因素的第q个水平值Xkq可由式(6)求得:
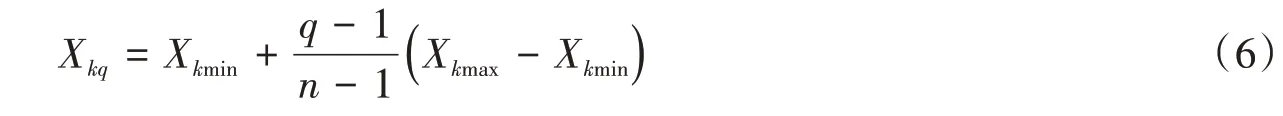
式中:Xkmin、Xkmax分别为第k个因素需要考虑的最值,主、亚谐分量的各阶相位角取值范围均为[0,2π],即Xkmin=0、Xkmax=2π。
结合均匀试验设计识别相位角可以通过调整均匀设计表的水平数n控制各因素的求解精度2π/n。因此,针对模型Ⅰ与模型Ⅱ分别设计5因素与10因素不同水平数n的均匀表,将相位角在[0,2π]上划分为n=10,25,50,100,500,1 000,1 500,2 000,2 500,3 000共10种情况,评估水平数n对识别精度的影响。
2.3.2 BP神经网络
参考神经网络相关算例及运算流程[10],基于2种步行荷载模型识别相位角并重构步行荷载,过程如下:
(1)BP神经网络的构建
根据荷载模型构建神经网络。模型Ⅰ中有5个未知量作为输入参数,即主谐分量前五阶相位角,所以输入层节点数为5,以采样频率为100 Hz的10 s步行荷载加速度时程作为输出量,相应的输出层节点数为1 000,隐藏层节点数设置为5,基于以上参数构建的BP神经网络结构为5-5-1 000。同样的,模型Ⅱ中考虑了亚谐分量的相位角,则有10个未知量作为输入参数,所以BP神经网络的结构为10-5-1 000。
(2)BP神经网络的训练与测试
BP神经网络的样本分为训练样本与测试样本,统计模型Ⅰ与模型Ⅱ的样本,如表2所示。BP神经网络以均方误差取最小值为目标,建立了各阶相位角与步行荷载的映射关系,对输入的不同水平相位角均匀表进行识别,寻找最优结果。

表2 BP神经网络样本Table 2 BP neural network sample
(3)重构步行荷载
基于相位角的识别结果,分别按模型Ⅰ和模型Ⅱ重构步行荷载,以步频为1.8 Hz与2.4 Hz的重构步行荷载为例,如图3所示。可以看出,相比模型Ⅰ,考虑了亚谐分量的模型Ⅱ能够清晰地体现行人左右脚的步行荷载差异。

图3 重构步行荷载加速度时程Fig.3 The reconstructed walking load acceleration time history
2.4 识别算法的敏感性分析
以均方根相对误差式(7)为标准,评价识别算法与重构步行荷载的准确性,分析亚谐分量与均匀表水平数对识别精度的影响。

式中:Fsc(t)为实测步行荷载时程;Fcg(t)为重构步行荷载时程;u为步行荷载时程数据点的个数。
2.4.1 水平数的影响
统计不同水平数n对均方根相对误差的影响,以步频为1.8 Hz与2.4 Hz的重构步行荷载为例,如图4所示。可以看出,随着水平数的提高,实测-重构步行荷载的均方根相对误差会产生波动,但整体呈下降趋势,说明可以通过控制均匀表的水平数提高识别方法的精度。同时应该注意到,当水平数大于500时,均方根相对误差基本趋于稳定,提高水平数对识别精度的影响十分有限,因此以水平数为1 000的相位角均匀表为训练样本,水平数为500的相位角均匀表为测试样本对步行荷载进行识别与重构。

图4 均方根相对误差与水平数的变化关系Fig.4 The relationship between RMSE and n
2.4.2 亚谐分量的影响
基于2种荷载模型重构步行荷载,限于篇幅,仅给出步频为1.8 Hz与2.4 Hz的实测-重构步行荷载加速度时程和荷载频谱进行对比,如图5~图8所示,统计实测-重构步行荷载均方根相对误差,如表3所示。
由表3可知,重构步行荷载与实测步行荷载的均方根相对误差最小值约为9%,最大值约为21%,均值约为15%,相比模型Ⅰ,除步频为1.8 Hz的重构步行荷载,基于模型Ⅱ重构的步行荷载均方根相对误差更小。由图5和图6可知,当实测步行荷载非周期性较强时,考虑了亚谐分量的重构步行荷载加速度时程与实测步行荷载加速度时程更为吻合。这说明当行人左右脚的荷载差异较大时,基于模型Ⅱ重构的步行荷载更接近真实步态。由图7和图8可知,基于模型Ⅰ重构的步行荷载不能反映亚谐波的存在,而基于模型Ⅱ重构的步行荷载准确地反映了各阶亚谐波,与实测步行荷载的荷载频谱十分吻合。这说明在重构非周期性较强的步行荷载时,不应忽略测试者左右脚的荷载差异,考虑亚谐分量的影响是必要的。
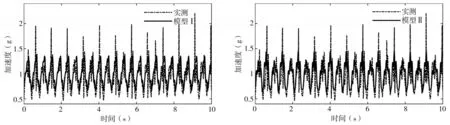
图6 2.4 Hz实测-重构步行荷载加速度时程Fig.6 Measured-reconstructed walking load acceleration time history at 2.4 Hz

图7 1.8 Hz实测-重构步行荷载频谱Fig.7 Measured-reconstructed walking load spectrum at 1.8 Hz

图8 2.4 Hz实测-重构步行荷载频谱Fig.8 Measured-reconstructed walking load spectrum at 2.4 Hz

表3 实测-重构步行荷载均方根相对误差Table 3 RMSE of measured-reconstructed walking load

图5 1.8 Hz实测-重构步行荷载加速度时程Fig.5 Measured-reconstructed walking load acceleration time history at 1.8 Hz
2.5 相位差统计
结合均匀试验设计建立BP神经网络识别得到步行荷载主、亚谐分量各阶相位角。由于一阶相位角容易受到试验起始时间与人为截取数据的影响,所以不考虑一阶相位角的具体取值,而关注各阶相位角与一阶相位角的差值。利用Lilliefors检验,通过MATLAB中的lillietest函数对相位角分布进行正态检验,如式(8)。

当h=0且p>0.05时,认为相位角φi服从正态分布。限于篇幅,仅给出模型Ⅱ中部分频率重构步行荷载的主、亚谐波各阶相位角的h和p,如表4。结果表明主、亚谐分量的各阶相位角均服从正态分布,并统计模型Ⅱ中各阶相位角的均值和变异系数,如表5和表6所示。可以看出,除步频为1.8 Hz的亚谐波分量二阶相位角与五阶相位角,其余步频各阶相位角均服从变异系数为30%~70%的正态分布。

表4 Lilliefors检验结果Table 4 Lilliefors normal test results

表5 模型Ⅱ主谐分量各阶相位角均值与变异系数Table 5 ModelⅡharmonic phase angle mean and variable coefficient
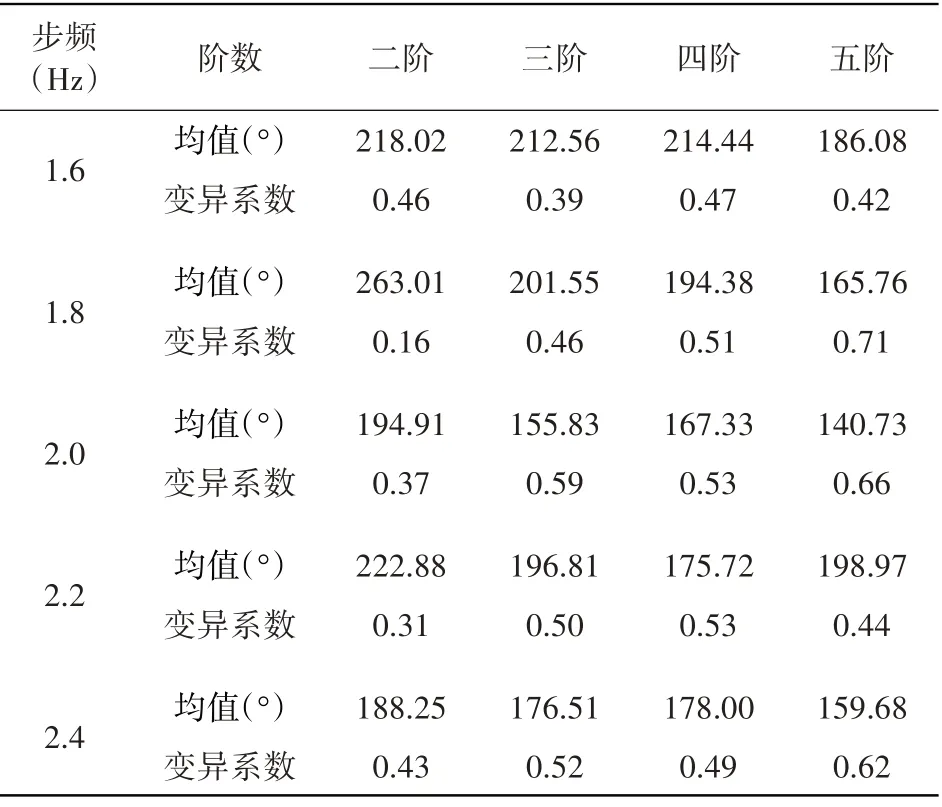
表6 模型Ⅱ亚谐分量各阶相位角均值与变异系数Table 6 ModelⅡsub-harmonic phase angle mean and variable coefficient
3 结论
文中提出了均匀试验设计与BP神经网络相结合的相位角识别方法,并基于模型Ⅰ和模型Ⅱ重构步行荷载得出以下结论:
(1)提高均匀表的水平数,可以提高该方法的识别精度与重构步行荷载的准确性,当水平数达到一定数值时,再次提高水平数对识别精度的影响十分有限;
(2)该方法识别的相位角精度较好,实测-重构步行荷载的均方根相对误差最小值约为9%,最大值约为21%,均值约为15%;
(3)当步行荷载非周期性较强,测试者左右脚的荷载差异较大时,应当考虑亚谐分量的影响,基于模型Ⅱ重构的步行荷载能更好地反映实际步态;
(4)结合均匀试验设计与BP神经网络识别得到的主、亚谐分量各阶相位角大致服从变异系数为30%-70%的正态分布。
