混合体系多塔矮塔斜拉桥推倒分析的适用性研究

2022-05-11周雨洁宋旭明

地震工程与工程振动 2022年2期

周雨洁，宋旭明，邹卓，唐冕

（1.中南大学土木工程学院，湖南长沙 410075；2.杭州市交通规划设计研究院有限公司，浙江杭州 310000）

引言

矮塔斜拉桥凭借美观、经济和刚度大和施工方便等优点，在修建梁式桥跨度过大、采用斜拉桥不够经济或者主塔高度受限时具有独特的优势，近年来得到广泛关注和应用。桥梁在地震作用下的响应分析是设计过程中的重要任务，目前常用的研究方法有综合运用反应谱法和动力时程分析法进行分析［1-4］和传统pushover分析法［5-6］。在矮塔斜拉桥抗震性能研究中，研究者大多仍采用反应谱和时程分析法，如Qu等［7］使用时程分析法研究独塔单索面矮塔斜拉桥桩土相互作用对结构动力特性及地震响应的影响，欧阳硕［8］采用反应谱法和时程分析法对环形矮塔斜拉桥进行确定性地震激励分析。

近年来，推倒分析方法作为一种结构非线性地震响应的近似计算方法，可以追踪结构从屈服到极限状态的整个非弹性变形过程，以其概念简明、操作简便、能用图形方式直观地表达结构的抗震能力与需求等特点，正逐渐受到重视和推广。［9］

21世纪初，Chopra等［10-11］提出考虑高阶模态影响的模态Pushover方法（modal pushover analysis，MPA），并运用此法对规则和非规则建筑进行了抗震需求评估。目前，MPA法在建筑领域有较为成熟的应用，在桥梁领域的研究始于Paraskeva等［12］将MPA引入桥梁抗震分析当中，并结合实例分析得出MPA较传统pushover方法更为精确。魏标［13］等运用MPA法对4座非规则连续梁进行横桥向地震位移需求的求解，通过与非线性时程分析对比，发现MPA能够合理的估计地震位移需求；曹飒飒［14］等运用MPA法和时程分析法对某多联合连续梁进行地震响应分析，发现MPA法可以对多联连续梁桥进行有效的抗震性能评估；申现龙等［15］以实际工程为例，通过与非线性时程分析对比，验证了Pushover方法用于CFST拱桥纵向地震需求评估的可行性。宋力等［16］采用MPA法与时程分析法对大跨度塔斜拉桥进行Pushover分析，验证了MPA法用于大跨度斜拉桥抗震性能评估的合理性。

在以往的研究者中，推倒分析多针对于连续梁桥、拱桥和常规斜拉桥，而运用于对矮塔斜拉桥进行抗震性能的研究较少，对采用MPA法对大跨径混合体系多塔矮塔斜拉桥的抗震性能研究少有相关文献。文中以某混合体系多塔矮塔斜拉桥为工程背景，分别研究结构弹性和弹塑性阶段地震响应，探讨推倒分析对于多塔矮塔斜拉桥抗震计算的适用性。

1 MPA法相关理论

1.1 基本原理与假定

推倒分析的基本思想是用具有一定分布规律的侧向力来模拟地震作用，通过将此侧向力不断单调递增作用于结构来分析结构的地震响应。计算时先建立结构有限元模型，使用等效的侧向力逐渐将结构推至事先确定的目标位移，研究结构在推覆过程中的弹塑性力学性能，由此评估整体结构或局部构件是否达到抗震设计的目标性能。

推倒分析理论基于以下2个假定［17］：（1）结构在地震作用下的响应只受基本振型控制，可用等效单自由度体系（SDOF）代替原结构多自由度体系（MDOF）进行分析；（2）结构沿高度方向的变形由位移形状向量ϕ表示。在整个推覆过程中，形状向量ϕ不会随着结构的变形而变化。

1.2 等效自由度的转换

用结构的顶点位移Xt（t）和形状向量ϕ来表示结构的位移向量X（t）：

定义单自由度体系的位移X*（t）为：

则可以得到多自由度结构相应的单自由度体系运动微分方程：

式中：M*、C*、K*分别为单自由度体系的等效质量矩阵、等效阻尼矩阵、等效刚度矩阵̈（t）为地震地面加速度；̈*（t）为单自由度体系的加速度；̇（t）为单自由度体系的速度。

其中：

式中：M、C、K为结构的质量矩阵、阻尼矩阵、刚度矩阵；I为单位向量。

在振型向量已知的情况下，单自由度体系的基底剪力和位移关系曲线可由多自由体系的基底剪力和顶点位移关系曲线转化求得。通过多自由度体系与等效单自由度体系的转化关系，对原结构进行推倒，求得等效单自由度体系在地震作用下的位移，反算出原结构的目标位移，然后再次对原结构推覆至目标位移即可评价结构的抗震性能。

1.3 模态推倒分析理论

模态推倒分析（MPA）由Chopra等［10-11］提出，并被验证应用于建筑结构是可行的。MPA分别采用与各阶模态相应的侧向力模式推倒结构，计算相应于各阶模态的地震响应，最后通过组合各阶模态的地震响应，得到结构总地震响应。MPA的基本实施步骤如下：

（1）建立结构的有限元模型，计算结构的动力特性，主要是结构的自振周期Tn和模态向量ϕn；

（2）对于第n阶模态，采用侧向力模式对mϕn结构进行推倒，得到结构的Vb-u曲线，其中，m为结构的质量矩阵，Vb为总的基底剪力，u为控制点位移；

（3）将Vb—u曲线转化成A—D能力谱曲线，即令：

其中，Mn为模态参与质量，Mn=(ϕTnm I)2/(ϕTnmϕn)，I为单位向量；Γn为模态参与系数，Γn=ϕTnmI)/(ϕTnmϕn)，I为单位向量；ϕm为控制点对应的ϕm值；

（4）将能力谱与非弹性需求谱组合后，可以求得第n阶模态的模态位移和基底剪力；

（5）按照一定方式组合上一步各模态的地震响应，得到结构总地震响应。

1.4 矮塔斜拉桥推倒分析实施

目前，针对多塔矮塔斜拉桥的抗震性能研究多采用反应谱法和动力时程分析法，文中将推倒分析方法应用于多塔矮塔斜拉桥地震响应的求解，具体思路如下：

（1）将推倒分析方法应用于多塔矮塔斜拉桥弹性地震响应的求解，在此阶段分别运用传统推倒分析和模态推倒分析（MPA）对多塔矮塔斜拉桥全桥进行推倒分析，然后将推倒分析结果与反应谱分析和线性时程分析结果对比。

（2）在进行弹性阶段的求解之后，评估传统模式推倒分析和MPA法能否较为准确的求解弹性地震响应，并判断是否应用这两种方法进一步求解多塔矮塔斜拉桥的弹塑性地震响应。

（3）进行弹塑性阶段地震响应求解，控制点的选取、侧向推覆力模式、振型的选择、以及结果组合方式均与弹性阶段推倒分析相同，性能点求解方法分别采用ATC-40能力谱法［18］和Chopra改进能力谱法，将这两种方法的求解结果与非线性时程分析对比，研究推倒分析是否能够较为准确的求解多塔矮塔斜拉桥的弹塑性地震响应。

推倒分析方法的主要工作是求得侧向荷载模式下结构的力-位移关系曲线，以及评价结构抗震性能。具体的实施步骤如图1所示［19］。

图1 推倒分析计算步骤图Fig.1 Step diagram of pushover analysis and calculation

文中以矮塔斜拉桥为工程背景对推倒分析进行适用性研究，具体分析步骤为：

（1）根据桥梁工程背景，利用有限元软件SAP2000建立模型；

（2）对桥梁进行反应谱分析，并根据加速度反应谱，利用SersmoArtif软件合成7条人工地震波，对该桥进行线性时程分析；

（3）将地震反应谱放大3倍，再合成7条人工地震波作为地震动输入，对结构进行非线性时程分析；

（4）对结构进行弹性推倒分析，并将结果与反应谱和线性时程结果对比分析，探究传统推倒和模态推倒在多塔矮塔斜拉桥地震分析中的优劣；

（5）对结构进行弹塑性推倒分析，并将结果与非线形时程结果对比分析，讨论模态分析中2种计算方法对该桥在塑性状态下的精确程度。

2 工程背景及有限元分析

2.1 工程背景

某多塔矮塔斜拉桥跨径组合为（120+2×210+120）m，三塔四跨式，B、C、D三个主墩，其中C主墩塔梁墩固结，B、D主墩设支座，塔梁固结，形成刚构-连续混合体系。该桥桥型布置如图2所示。索塔采用独柱式钢筋混凝土结构，截面为八边形，塔高35 m，主塔截面顺桥向等宽段厚5 m，塔底10 m范围，宽度由5 m渐变到6 m，横桥向3 m宽。斜拉索为单索面双排索，采用Φs15.2 mm型环氧涂层钢绞线拉索体系，在塔上采用分丝管式索鞍通过，梁上索距4.0 m，塔上索距1 m。桥塔立面布置图见图3（a）。主梁为预应力混凝土变截面箱梁，采用整幅式斜腹板单箱三室截面。箱梁顶板宽38.50 m，底板宽16～19 m，悬臂长8.25 m。跨中截面梁高4.1 m，支点截面梁高7.3 m；中腹板厚0.65 m，边腹板厚1.2 m。详细数据见图4（a）。主墩采用钢筋混凝土花瓶式桥墩，纵桥向厚度5.5 m，墩顶5 m和墩底3 m范围内为实心，其余为空心，壁厚顺桥向和横桥向均为1.2 m。主墩下接5.5 m厚的承台，平面尺寸为15 m（横）×25 m（纵），承台下设15-Φ2.5 m群桩基础，布置3排，每排5根。主墩立面图详见图3（b），主墩和桥塔关健截面图详见图4（b）、（c）。

图2 桥型立面布置图Fig.2 Layout of bridge elevation（unit：cm）

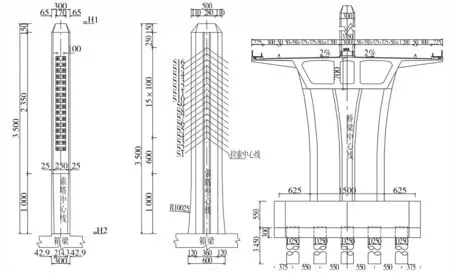
图3 桥塔及主墩立面布置图Fig.3 Layout of tower and main pier elevation（unit：cm）

图4 主梁、主墩和主塔截面图Fig.4 Sectional drawing of main beam，main pier and main tower（unit：cm）

2.2 有限元模型

采用有限元程序SAP2000建立空间有限元模型，主梁、主塔和桥墩均用梁单元，斜拉索采用桁架单元，主梁和斜拉索以及桥塔与拉索锚固区用主从关系模拟，综合考虑地质条件，以及研究目的，忽略桩基础和相邻引桥耦联振动的影响，故直接对墩底进行固结处理。C墩的塔梁墩固结；B和D墩的塔梁固结，主梁与主墩之间设置一般支座，忽略支座的非线性，墩塔采用mander本构；A和E墩约束主梁横向位移，全桥有限元模型如图5所示。在主墩墩底、主塔与主梁以及C号墩梁的交界处采用全约束，其余的墩梁之间横竖向平动和绕纵桥向转动予以约束。文中研究时采用轴力弯矩（PMM）相关的集中数值铰模拟，塑性铰的位置设置在该桥各墩墩底、刚构桥墩的墩顶。由于矮塔斜拉桥主塔刚度较小，同时在反应谱分析和线性时程分析时发现各塔塔顶位移远大于墩顶位移，为了研究在地震作用下主塔屈服的可能性，在各主塔塔底也设置了塑性铰。

图5 全桥有限元模型Fig.5 Finite element model of full bridge

2.3 地震波的选取

根据本桥地震安全性评价报告，桥位区50年10%超越概率动峰值加速度大于0.05 g，地震动反应谱特征周期为0.4 s，对应地震基本烈度为Ⅵ度，按Ⅶ度设防，本桥桥址区场地类别属Ⅱ类。经过试算发现，在Ⅶ度E2地震作用下，该桥横向和纵向均处于弹性状态，因此在进行反应谱分析时，根据Ⅶ度E2设计加速度反应谱，利用SersmoArtif软件合成7条人工地震波，地震波加速度反应谱曲线与设计加速度反应谱曲线对比图如图6所示。由此可知，人工地震波加速度反应谱和设计加速度反应谱匹配性良好。

图6 E2加速度反应谱对比图Fig.6 E2 acceleration response spectrum comparison chart

为了研究推倒分析在该桥的弹塑性地震响应的适用性，有必要进行非线性时程分析，为后续分析提供对比依据，试算后，将Ⅶ度E2地震反应谱放大3倍后该桥进入塑性状态，人工地震波加速度反应谱曲线与3倍Ⅶ度E2设计反应谱曲线对比如图7所示，两者依旧匹配性良好。

图7 放大的加速度反应谱对比图Fig.7 Magnified acceleration response spectrum comparison chart

2.4 动力特性分析

根据SAP2000全桥有限元模型，运用多重Ritz向量法计算出结构的自振特性，取其前100阶振型，此时结构顺桥和横桥向的振型参与质量已达到95%以上。将纵横向振型参与质量大于1%的模态参数分别列入表1～表2。

表1 纵向主要振型Table 1 Main vibration mode in longitudinal direction

表2 横向主要振型Table 2 Main vibration mode in horizontal direction

3 弹性推倒分析

传统Pushover分析是一种估算结构弹塑性地震响应的近似方法，其计算精度受加载模式的影响，不如时程分析法，但优点是可避免地震波选择的不确定性，同时通过设置推倒终止指标，可一定程度上反映结构的抗震能力［20］。但对于高阶模态对结构抗震性能影响较大的结构，传统推倒分析往往失真，因此研究人员提出多模态推倒分析方法及其改进方法对结果进行修正，MPA法优势突出：考虑高阶振型影响，且计算过程无需计算各阶模态实时动力特性，用SAP2000、MIDAS等即可实施［21］。文中首先对全桥顺向和横向分别进行传统荷载模式推倒分析和模态推倒分析（MPA），然后将分析结果与反应谱和线性时程结果进行对比，评估多塔矮塔斜拉桥处于弹性状态下2种推倒分析方法的精确性。

对该矮塔斜拉桥分别进行顺桥向和横桥向的反应谱分析和线性时程分析，反应谱分析采用前100阶振型，线性时程分析时阻尼选用瑞利阻尼，顺桥向瑞利阻尼选择第1阶和第10阶模态计算，横桥向瑞利阻尼选择第4阶和第18阶模态计算。经计算时程分析地震波的选取和瑞利阻尼的取值是合理的。

3.1 传统荷载模式推倒分析

在进行传统荷载模式推倒分析时，控制点选取结构最大位移处，即顺桥向的中塔C塔顶，横桥向的边塔B塔顶。侧向推覆力模式选取6种侧向荷载分别进行推倒，性能点使用能力谱法进行求解，由于处于弹性阶段，能够准确的求解性能点。传统荷载模式推倒分析纵横向性能点求解如图8所示，易知在传统荷载模式下横纵向均处于弹性状态。

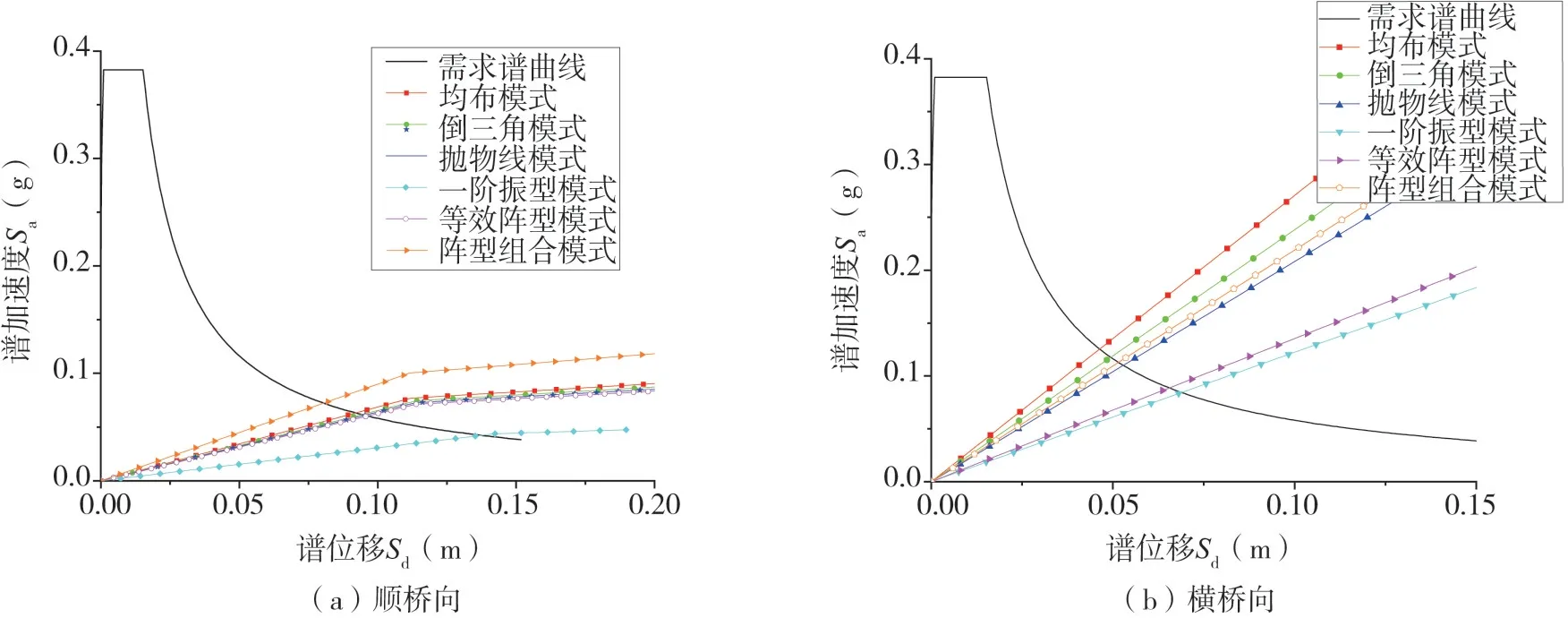
图8 纵横向性能点求解图Fig.8 Schematic diagram of solving performance points in the vertical and horizontal direction

顺桥向与横桥向推倒分析性能点求解结果如表3所示，普遍认为时程分析法是较为准确的分析方法，但反应谱法的求解效率更高，从表中易看出时程与反应谱相差不大，故选取反应谱法的结果作为基准。综合顺桥向和横桥向传统模式推倒分析的性能点求解结果，可以看出反应谱和传统推倒分析的求解有较大的偏差，甚至在顺桥位移偏差均值达到183%。究其原因，传统推倒分析方法一般对结构在第一阶振型控制下的地震响应有较好预测，但多塔矮塔斜拉桥除第一阶振型外，高阶振型对地震响应也有较大影响，因此传统模式推倒分析不适合求解多塔矮塔斜拉桥的地震响应。

表3 传统分析性能点的求解对比结果Table 3 Solution comparison results of performance points in traditional analysis

3.2 多模态推倒分析（MPA）

在进行多模态推倒分析时，应选取参与质量大于1%，且保证所选振型模态参与质量总和大于90%的振型。计算时顺桥向选择第1、3、6、10、29、36阶，总的振型参与质量系数达到94.9%；横桥向选择第4、8、12、13、15、18、51阶，总振型参与质量系数达到91.3%；控制点选取各阶模态振型位移最大的节点，具体见表4。性能点使用能力谱法进行求解，最后运用SRSS方法组合各阶模态结果求得结构总地震响应。

表4 各阶模态控制点位置Table 4 Position of control points of each mode

考虑到各阶模态所选控制点位置不同，在求解结构总地震响应时性能点统一转换成C塔顶。由表5 MPA分析性能点的弹性求解知，MPA法求解偏差不大，且顺桥向、横桥向的位移偏差值仅在1%以内，可以看出，针对该桥型MPA法在评估位移响应值时精确度满足工程要求。对关键位置分别用反应谱、时程分析法和MPA法计算地震响应，从图9可知：反应谱和MPA分析在顺桥向地震响应的求解偏差基本在20%之内，经计算C墩和C塔的位移和内力的求解偏差基本在5%之内。

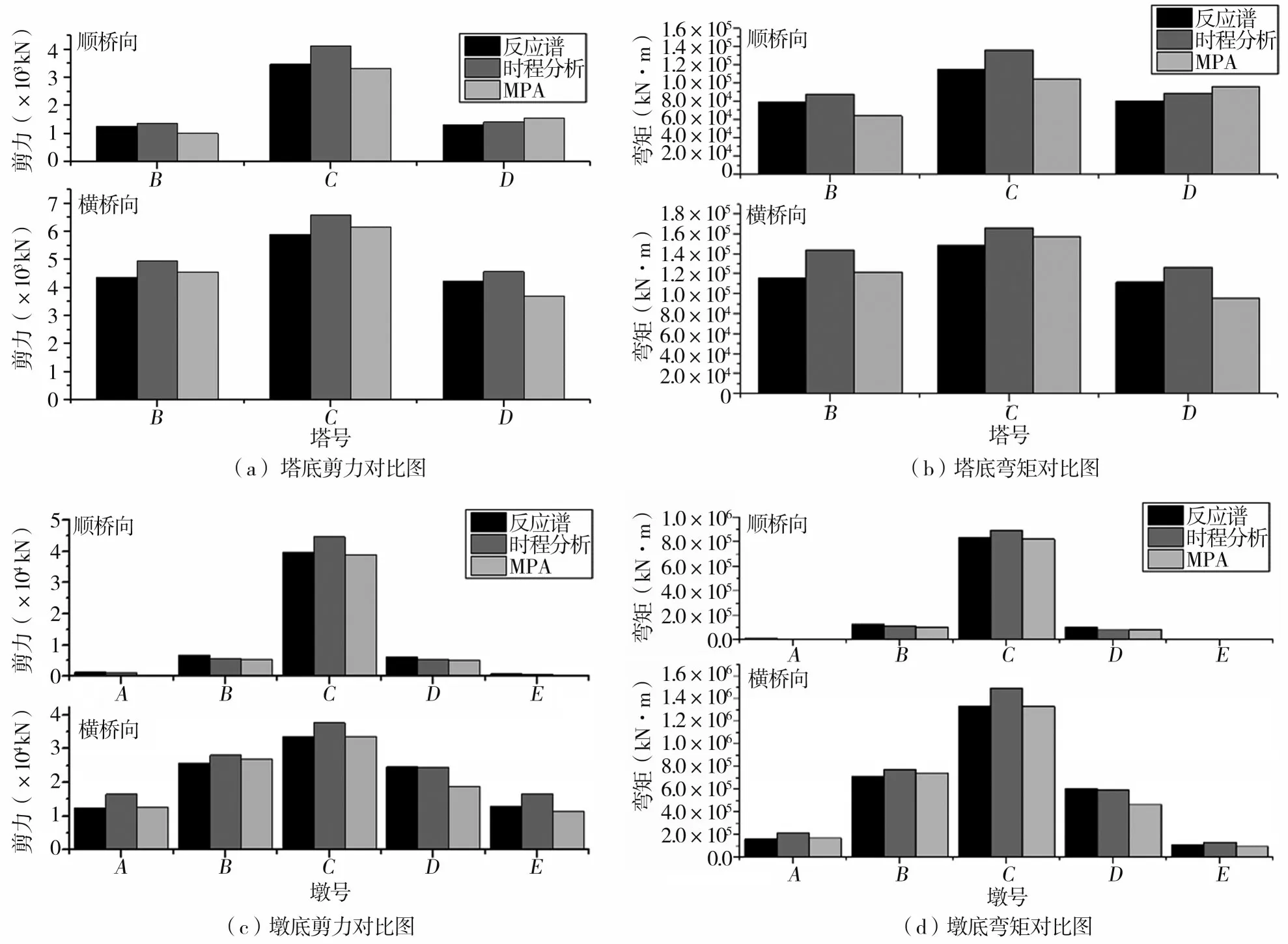
图9 反应谱、线性时程分析及MPA法内力对比图Fig.9 Internal forces of response spectrum method，elastic time history analysis method and MPA method

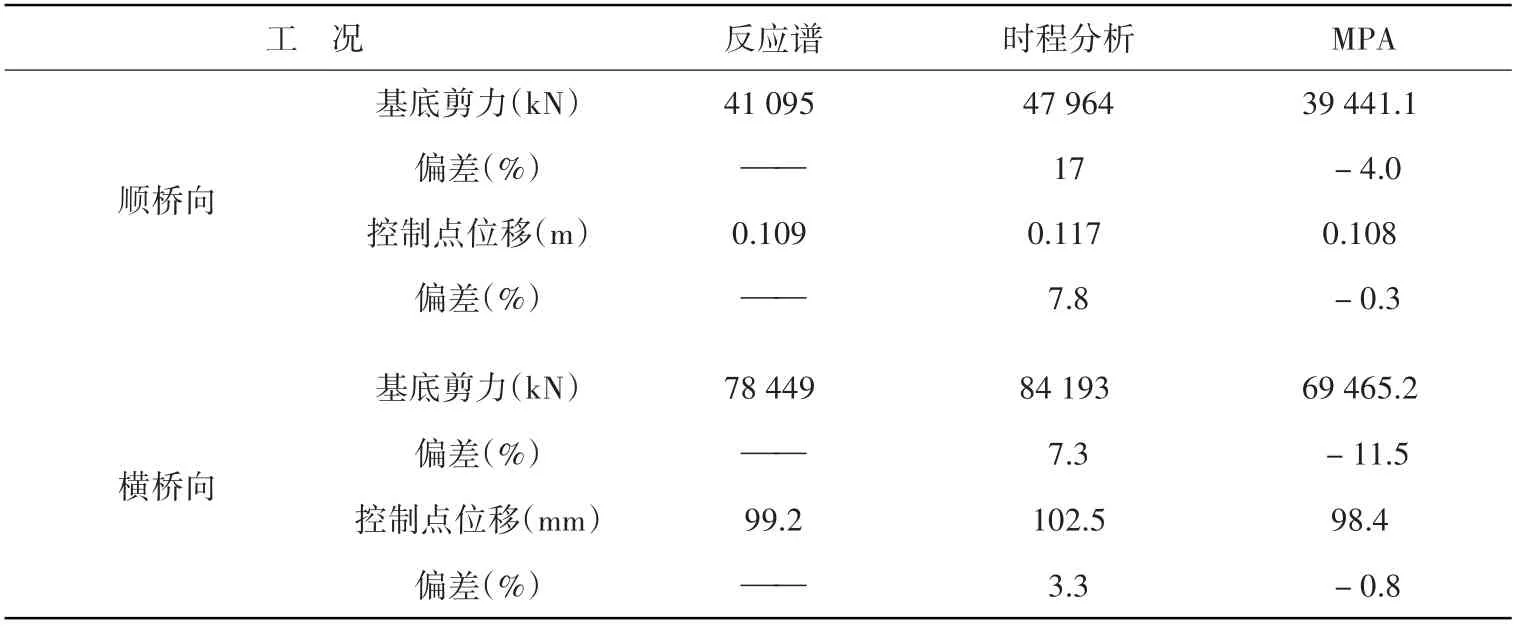
表5 MPA分析性能点的弹性求解对比结果Table 5 Elastic solution comparison results of performance points in MPA analysis

由于本桥为混合体系矮塔斜拉桥，只有C墩的塔梁墩固结，纵桥向其他墩都是活动支座，因此在顺桥向所选的模态参与质量较大的6阶振型中，A和E墩位移为0，并未产生振动，B和D墩分别只在29阶和36阶才有结果，产生局部振动，因此出现求解偏差。在多选择2个纵向活动墩产生振动的模态进行推倒计算之后，发现纵向活动墩的位移和内力求解偏差减小至10%以内。而在横桥向地震响应的求解中反应谱与MPA推倒分析的偏差基本都在15%之内，因此，MPA法对横桥向地震响应的求解准确性较高。综合上述分析，可得对弹性状态下的混合体系矮塔斜拉桥进行地震评估时MPA法较传统推倒法更为精准。

4 弹塑性推倒分析

通过上面对比分析，易知传统推倒分析在求解该桥型弹性阶段地震响应有很大偏差，随后在弹塑性地震响应分析中仅采用MPA法。在实施MPA法时，模态的选择、控制点的选取和模态结果组合方式与弹性模态推倒分析相同，但性能点求解分别采用ATC-40能力谱法和Chopra改进能力谱法，将求解结果与非线性时程分析结果对比，研究MPA推倒分析方法在混合体系矮塔斜拉桥弹塑性地震响应分析中的适用性。

考虑到各阶模态所选控制点位置不同，采用同上处理。在图7所示的3倍Ⅶ度E2地震波作用下，进行非线性时程分析，将其结果（7条波平均值）作为标准来探究该桥在塑性状态下ATC-40能力谱法和Chopra改进能力谱法的求解准确性。由非线性时程知，在顺桥向地震作用下，仅在中墩C墩底出现塑性铰；而在横桥向地震作用下，中墩C首先出现塑性铰，之后中塔塔底出现塑性铰，最后两边塔塔底出现塑性铰，而在其他位置未出现塑性铰。这表明在横向地震作用下塔底相较于主墩顶更薄弱，在设计中应对塔底进行特殊处理加强。

4.1 顺桥向分析

顺桥向MPA法性能点求解图示见图10（a），可以看出顺桥向仅第3阶推倒分析性能点进入塑性状态。下面分别运用ATC-40能力谱法和Chopra改进能力谱法求解第3阶推倒性能点，求解图示见图11。组合各阶模态推倒结果，结构在3倍Ⅶ度E2地震下的性能点求解偏差见表7（a），可知：ATC-40能力谱法和Chopra改进能力谱法的求解偏差都在20%之内，且2种方法的求解偏差相差很小。

图10 纵横向性能点求解图Fig.10 Schematic diagram of solving performance points in the vertical and horizontal direction

图11 第3阶推倒性能点求解图Fig.11 Solution graph of the third-order downturn performance point

非线性时程和MPA法所计算的各关键位置的地震响应如图12所示。由图12顺桥向分析可知：ATC-40法和Chopra的求解偏差相当，对位移的求解偏差较小，基本在15%之内；对塔内力的求解偏差基本在25%之内；对墩底弯矩的求解偏差较大，C墩和D墩墩底弯矩偏差超过30%，但是用推倒分析来评估地震下的墩底内力会较为保守。

图12 非线性时程分析、ATC-40能力谱法和Chopra改进能力谱法内力对比图Fig.12 Internal forces of non-linear time history analysis method，ATC-40 capacity spectrum method and Chopra improved capacity spectrum method

表6中顺桥向可得MPA对墩底塑性转角的求解偏差也很大，其原因与建模时采用的轴力弯矩（PMM）相关铰有一定关系。2种方法计算时墩轴力变化幅度不同，MPA法分析时墩轴力变化幅度较小，而非线性时程分析时变化幅度大。在墩底取相同的弯矩值时，时程分析恒载轴力与动轴力组合后的值较小，轴力弯矩（PM）屈服面上的屈服弯矩相对较小，从而塑性铰转角比MPA法分析时大。

表6 塑性转角求解偏差Table 6 Plastic turning angle solution deviation rad

4.2 横桥向分析

图10（b）得出仅第4、8、12阶推倒分析性能点进入塑性状态，采用与顺桥向同样的方法，分别求出结构在3倍7度E2地震下ATC-40能力谱法和Chopra改进能力谱法的位移、基底剪力以及该桥各关键位置的地震响应。

由表7（b）知，ATC-40法和Chopra的求解偏差相当，且控制点位移偏差都在10%之内，而塔底弯矩的求解偏差较大，虽然B墩和C墩墩底弯矩偏差有50%，但采用模态推倒分析塔底内力会比较保守。此外各墩墩底内力的求解偏差都在20%之内。MPA对塑性转角的求解偏差出现和顺桥向同样的现象。

由表7可知，ATC-40能力谱法和Chopra改进能力谱法的求解偏差都在25%之内，且两种计算方法求解偏差之间相差很小，可见两者在多塔矮塔斜拉桥的塑性地震响应求解方面基本具有良好的统一性。

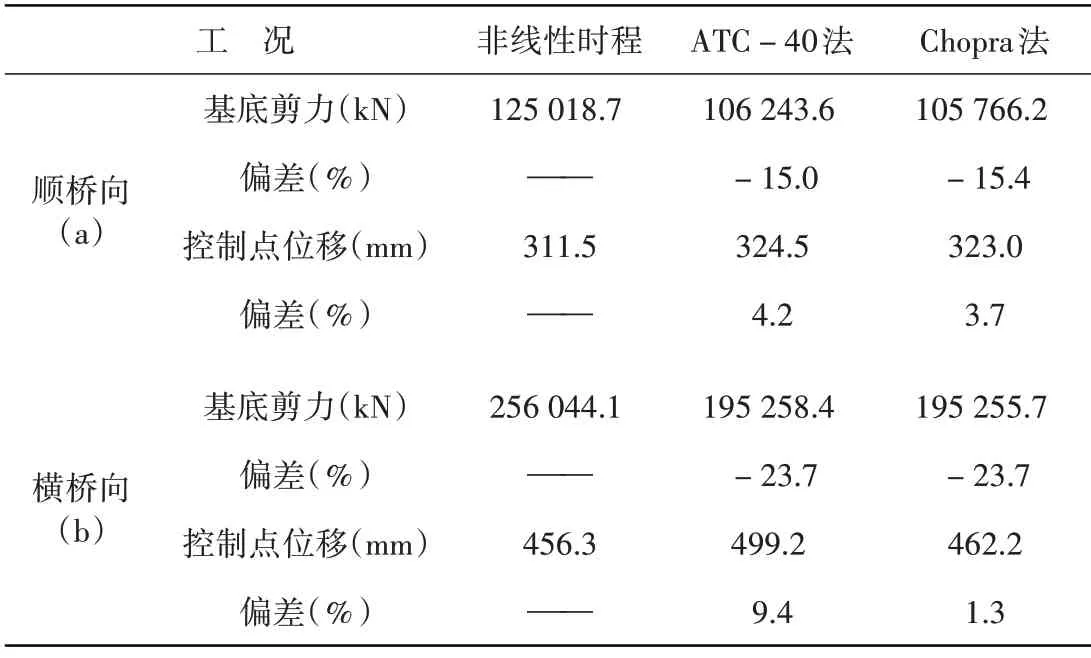
表7 MPA分析性能点的弹塑性求解对比结果Table 7 Elastoplastic solution comparison results of performance points in MPA analysis

该桥进入塑性状态后，两种计算结果在纵横向基底剪力与非线性时程偏差较大，均在15%以上，说明这两种性能点求解方法在对基底剪力的预测存在误差，可能由于多塔矮塔斜拉桥的结构特性，将总响应性能点统一到C塔顶后，忽略其他模态控制点的影响，造成内力预测出现偏低现象，建议运用ATC-40和Chopra法计算混合体系多塔斜拉桥地震下内力响应时，需要综合考虑其他模态控制点的影响。从控制点位移来看，通过这两种计算方法算出来的结果偏保守，且偏差均在10%以下，因此针对该桥的地震位移响应预测分析依旧是可靠的。MPA法对混合体系多塔矮塔斜拉桥评估关键响应量还是能做出有效评估的，与时程分析相比，时间大大缩短，可用于此类桥梁的初步抗震设计。