基于MEEMD和时变VARMA模型的地震动噪声清除及基线修正

余华龙，徐国林

（西南林业大学土木工程学院，云南昆明 650224）

引言

地震灾害是一种频发的自然灾害，它会危害人们的生命，对人类的财产造成巨大损失。对地震的监测、预警和地震记录的研究是降低地震灾害必不可少的环节。地震动信号处理是地震记录可以在工程中应用的基础。

强震仪记录的加速度信号常用于研究结构承受的地震作用特性。研究人员指出地震动中低频成分会对大体量、长周期的建筑产生巨大破坏，记录中低频成分在信号处理中如何保证精度不容忽视。

信号处理的目的就是最大程度地保留真实信号去除其它噪声信号。地震动信号去噪时，目前采用的方法有除趋势项的时域修正算法、基于高通滤波与数值积分法、基于FFT变换和频域计算的方法、小波分析法、EMD等。去除趋势项的时域修正算法：采用多项式拟合方法去除对振动加速度信号积分后得到的速度和位移曲线的常数项和趋势项［1］。但这种方法会受到滤波器过渡带和数值计算误差影响，计算的位移曲线误差较大，且此积分方法不适用于含有复杂噪声的信号。基于高通滤波与数值积分的方法：利用高通滤波器修正加速度信号中精度低于1 Hz频率以下的成分及数值积分后出现的趋势项［2］。这种方法虽然可将大部分长周期噪声滤除，但在滤除低频噪声的同时，也将地震动的低频成分也一并滤除，另外还存在滤波器过渡带和多次滤波带来的计算误差，导致处理结果精度较低。基于FFT变换和频域计算的方法：利用谐波信号的时-频关系，由振动加速度频谱得到速度和位移频谱，再对振动速度频谱和位移频谱进行傅里叶反变换，得到速度和位移时间历程曲线［3］。这种方法虽然精度高、计算速度快，但是并不适用于非稳态信号，对工程实际来说，这种方法指导性并不高。积分法在处理地震动信号时，由于加速度传感器在1 Hz以下的测量精度较低，而且这些低频部分经积分后对位移信号有显著的影响，故首先滤除了信号中小于或等于1 Hz的低频部分［3］，这也意味着部分有效低频信号被滤除。小波分析法是一种先验的信号处理方法，必须预先设定小波基函数，而且选择不同的小波基函数对数据处理的结果影响甚大。肖梅玲等［4］对不同小波基下的结构位移反应进行深入研究也证实了这一点。EMD算法由于理论体系不完整、端点效应、IMF筛分准则和模特混叠等问题，有的时候信号处理效果并不如预期那样。但是Huang等在借助EMD进行噪声辅助分析的过程中发现，因为一些尺度的缺失，将导致非纯噪声信号出现模态混叠问题。在实际工程中，记录的信号往往是非纯噪声信号，为避免存在模态混叠问题，通常的做法是在其中引入正、负成对的白噪声同时为了降低加入的噪声集合次数，提高计算效率，消除重构信号中残余辅助噪声。

信号处理方法还存在着滤波效果不理想的问题，不能很好地完成去除地震动信号基线漂移和底噪信号处理的任务［5］。所以众多研究者仍在改进基线修正和低频噪声信号处理方法领域做深入的研究。

针对上述方法的不足，文中提出一种基于改进集合经验模态分解（简称MEEMD）的地震动信号基线漂移去除方法。以MEEMD作为基础来预处理信号，利用排列熵算法去除随机性较大高频噪声信号，然后将剩余信号通过EMD分解得到本征模态函数（IMF），利用时变向量自回归模型（简称VARMA）还原地震动信号，而后借助时变VARMA模型对从MEEMD预处理获取而来的IMF进行建模，以最大限度地还原真实的地震动信号。

1 EMD的不足

作为对非平稳信号以及非线性信号进行处理的一种方式方法，经验模态分解（简称EMD）属于一种后验的、直观的以及直接的信号处理手段。相比小波分解以及傅里叶分解而言，EDM是将数据的时间尺度特征作为基本依据来对信号进行分析处理。除此之外，EMD兼顾了小波变换所具有的高分辨率优势。从理论层面来看，EMD能够应用于任何类型信号的分解过程。

但EMD算法还有以下几个方面的问题：

首先，关于EMD算法涉及的基本理论尚且存在诸多需要完善的部分，同时没有配备十分严谨的数学理论和基础模型，一般情况下只能单纯依靠试验形式来对其唯一性、正交性以及收敛性等基本特征进行求证，无法从数学理论上来进行证明。针对EDM分析方法应该使用于何种信号处理也没有形成统一的界定和合理的解释。针对本征模态函数而言，只能借助十分有限的例子经验以及窄带信号对应过极值点同过零点之间的关系里面获取关于IMF的具体定义，并且实际效果并不理想。即便大多数例子均体现了EMD结果具有的合理性以及直观性，但是具体理论框架部分仍需要进一步完善和论证。

其次，在EMD算法中计算包络平均时，主要应用的3次样条插值法，在计算过程中往往会产生下冲、过冲等问题，此种方式获取的IMF无法严格保证包络具有完全对称效果。在大多数情况下，针对原始信号而言，其端点位置并非是极值点位置，在拟合过程中会因为边界摆动，在一定程度上会引发计算偏差，进而导致信号两端存在发散的情况。随着筛分的不断开展，此种发散问题开始朝着内部传播，最终使得分解结果严重偏离实际信号，产生假频信号。

最后，在进行EMD分解时，对于同一个IMF分量往往会存在不同频率或者不同尺度信号，亦或是同一频率或者同一尺度的信号经过分解以后，会进入到不同的IMF分量里面，这便是所谓的模态混叠。假如信号里存在无法消除的噪声干扰，以及间歇信号的情况，使用EMD分解将会导致单个基本分量中存在多尺度成分的问题。由此可知，只要出现模态混叠，势必会影响后续分解分量。因此，从物理层面来看，整个EMD分解的结果不具备实际意义。

2 MEEMD的具体改进方法

针对以上问题，有必要对经典的EMD算法进行改进，具体改进措施如下；

对特定信号x（t）进行处理的过程中，有效的MEEMD分解过程，一般包含如下几个步骤：

（1）将n组辅助白噪声引入到原始信号里面，采取正、负成对的引入方式，从而得到包含2n个信号的信号集合，其中S和N分别代表的是原始信号和辅助噪声信号，M1、M2则分别代表的是加入正、负成对噪声以后对应辅助信号；

（2）利用EMD分解集合里面所有信号，并且获得相应的IMF分量，用Cij来表示第i个信号对应的第j个IMF分量；

（3）借助多组分量组合的方式获取分解结果，即：

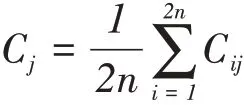
检查Cj是否为异常信号。如果信号的熵值大于θ0，则被认为是异常信号，否则近似认为平稳信号。θ0取0.55～0.6较为合适；

（4）假如Cj属于异常信号，那么便需要继续筛选，直到其属于非异常信号为止；

（5）在原始信号中分离出已经完成分解的前p-1个分量，即：

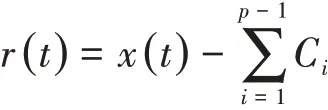
（6）再对剩余信号进行EMD分解，得到n个IMF，r2=r1-c2，...，rn=r n-1-cn，当rn是单调函数或是一个极小的常量时，就无法再提取IMF，停止分解过程，得到下面式子：

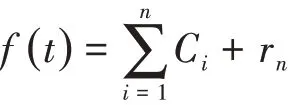
残差rn是信号f（t）的集中趋势，IMFs（c1，...，cn）主要涵盖不同时间特征以及不同尺度大小的信号成分，同时按照尺度由小到大的顺序进行排列。由此可知，对于不同频率段而言，对应频率成分是存在差异的，并且随着f（t）变化发生改变。

3 利用时变VARMA模型还原地震动信号

由于MEEMD分解后得到的残差一般为常数或单调的趋势项，因此在后续步骤中不考虑［8］。

（1）将所有的IMF用时变VARMA（p，q）模型表示

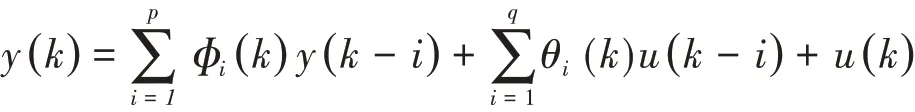
上述式子里，y（k）主要由n个IMF构成，即：

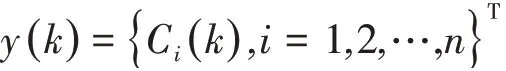
其中，滑动平均系数θi（k）同自回归系数Φi（k）均属于n阶方阵。u（k）属于n维零均值高斯白噪声过程，对应方差为Q（k）。（由于在还原过程中不再添加噪声信号，因此本文中u（k）取0）。其中k指某个时间点t，即t=k·Δt；Δt指的是采样时间间隔值。考虑到所有n个IMF代表的都是相互正交单分量信号，因此，可以将其看作是，自由度为n的时变系统对应的n个输出，此时，能够通过n维时变VARMA（2，1）模型来进行表示。

（2）将时变VARMA（p，q）模型表示为状态-空间模型的形式

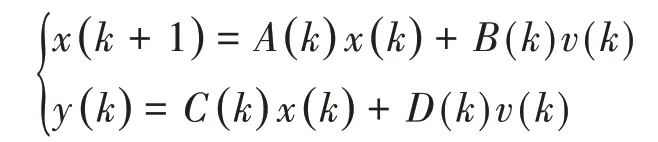
矩阵A（k）、B（k）、C（k）和D（k）称为模型参数，且

（3）借助Kalman滤波基本方法，对A（k）以及B（k）进行估算。

（4）参照公式仿真、验证各IMF，最终将获取的IMF进行求和处理，即得到地震动加速度信号图。

由文献［8］知，时变VARMA（2，1）模型属于最佳模型，不需要结合AIC等基本准则对模型阶数进行判断。时变VARMA模型本质上属于参数化模型，在拟合精度方面具备较高水平，同时此模型还兼顾了地震动频域以及时域分布特征［8］。

通过VARMA模型，将IMF还原为地震动信号，此时的地震动信号是完全去除噪声和进行基线修正后的信号，即“真实信号”。

最后，针对此“真实信号”利用文献［13］所提方法，进行连续小波变换，进而得到地震动信号的位移信号。

4 算例验证

由于目前还没有能自动去除低频误差的方法。相对而言，小波分解截断法的基线修正的处理能力强，能应对许多低频误差成分复杂的情况。所以文中选用以小波分解截断法处理的结果来作为参考。

根据前文的分析及总结，获取位移记录，具体处理步骤如下：

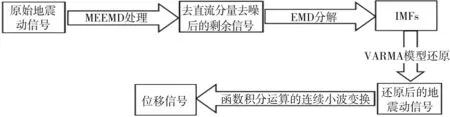
图1 地震动降噪、积分流程图Fig.1 Ground motion noise reduction and integration flow chart

下面按照上述步骤进行算例验证：

（1）原始地震动信号。

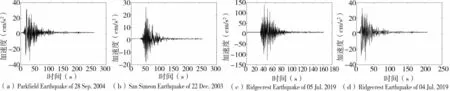
图2 原始地震动加速度信号Fig.2 Original earthquake acceleration signals

（2）通过MEEMD处理后得到的信号。

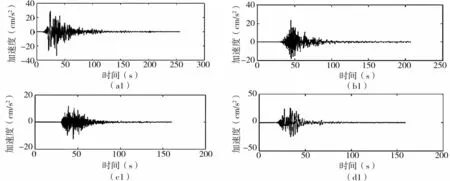
图3 基于MEEMD模型处理的地震动信号Fig.3 Signals processed by MEEMD model

（3）对剩余信号进行4次EMD分解后的结果。

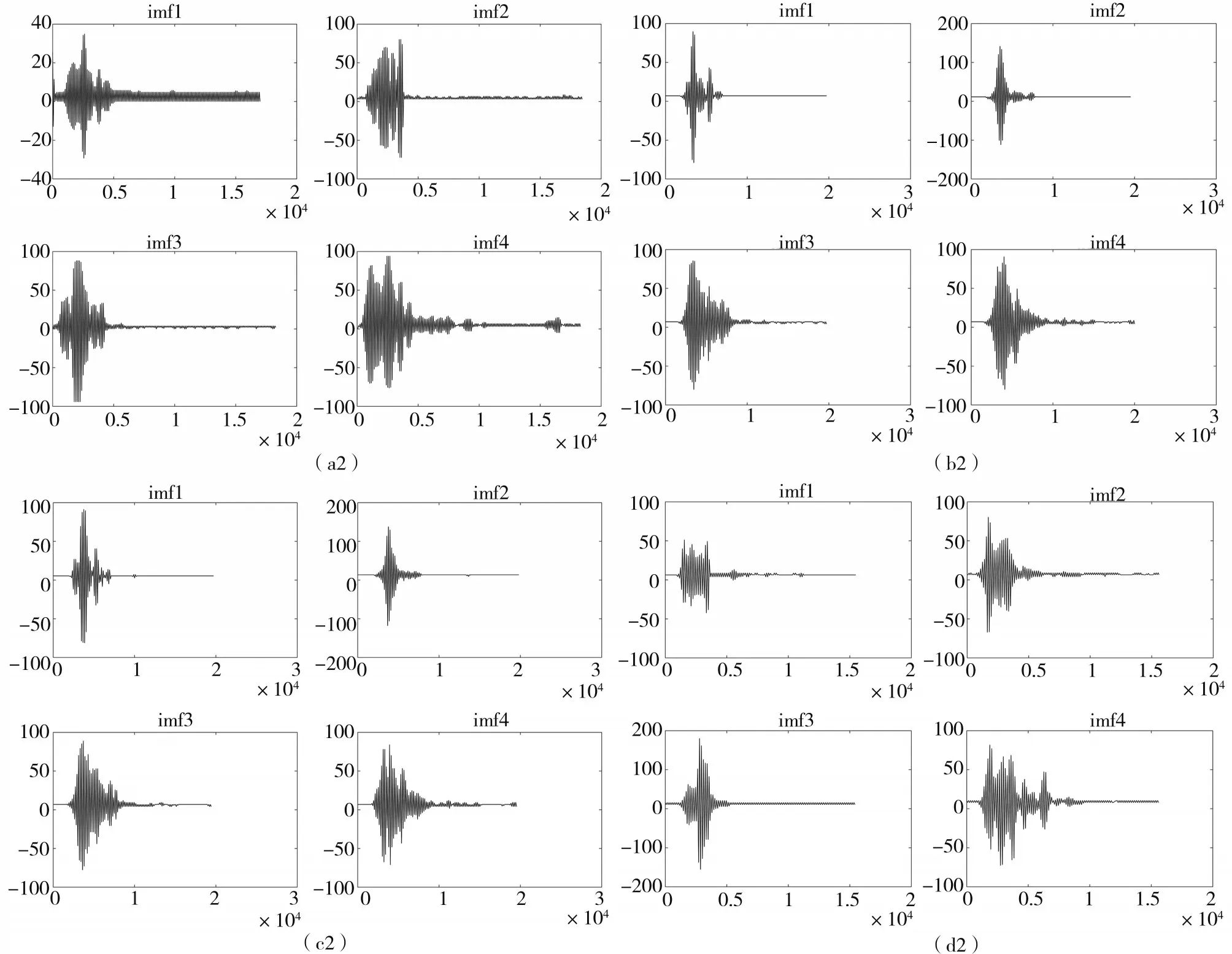
图4 EMD分解后IMFFig.4 The IMF after EMD decomposition

图4 （续）Fig.4（Continued）

（4）利用VARMA模型将所得的所有IMF仿真还原为地震动信号。

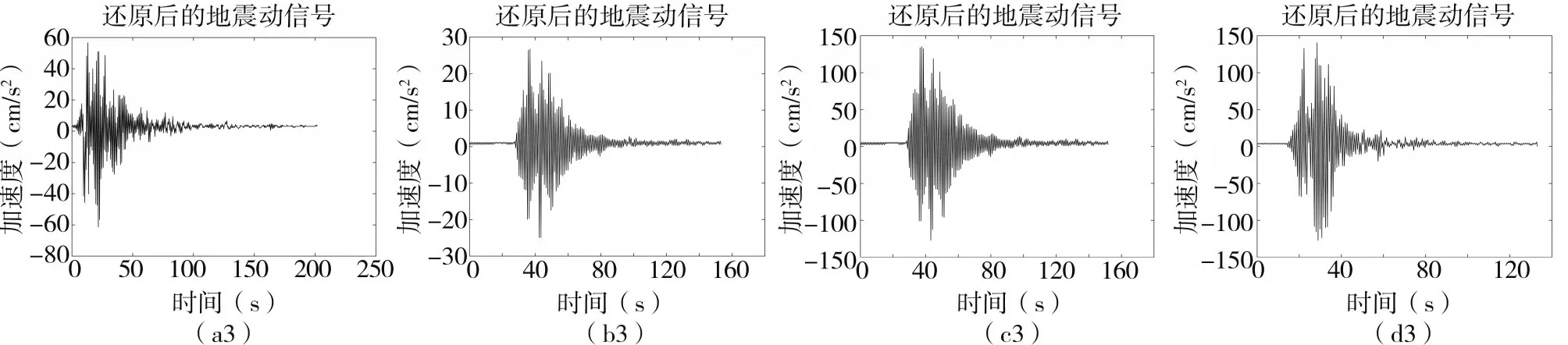
图5 基于VARMA模型还原的地震动信号Fig.5 Earthquake signals restored by the VARMA model

（5）对去噪后的信号进行函数积分运算的连续小波变换，得到位移信号。

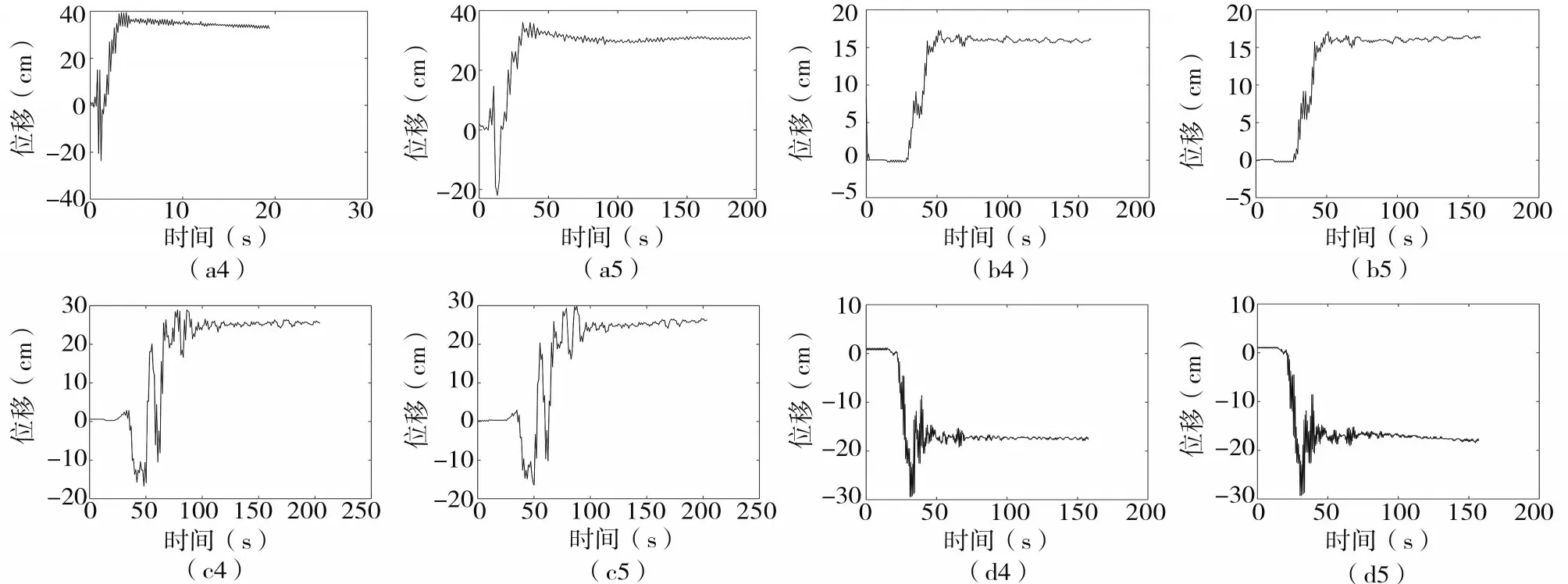
图6 基于本文方法（左）与小波分解截断基线修正法（右）获得的位移信号Fig.6 Displacement signal processed by the method in this paper（on the left）and the wavelet decomposition truncation baseline correction method（on the right）

（6）实验结果分析。

对比以上4组数据的位移处理结果（a4与a5、b4与b5、c4与c5、d4与d5对比），不难发现文中方法与小波分解截断基线修正法处理得到的位移信号曲线基本吻合，证明本方法是可行的，能够实现基线校正。

5 算例正确性的充分验证

选取日本“3·11”强震中与GPS台站相距5 km内的3个台站强震记录进行研究，对比同震位移和文中方法处理加速度记录获得的永久位移的差别，验证文中方法的精度。用文中方法处理EW向的强震加速度记录，处理过程如下所示。

（1）原始地震动信号。

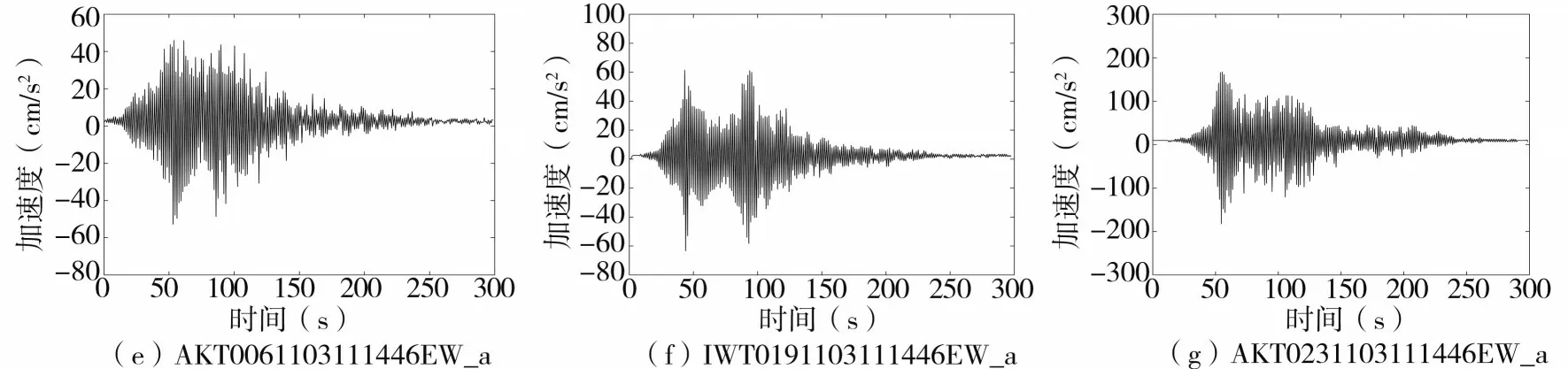
图7 日本3.11原始地震动加速度信号Fig.7 Original earthquake acceleration signals of Japan 3.11 earthquake

（2）通过MEEMD处理后得到的信号。

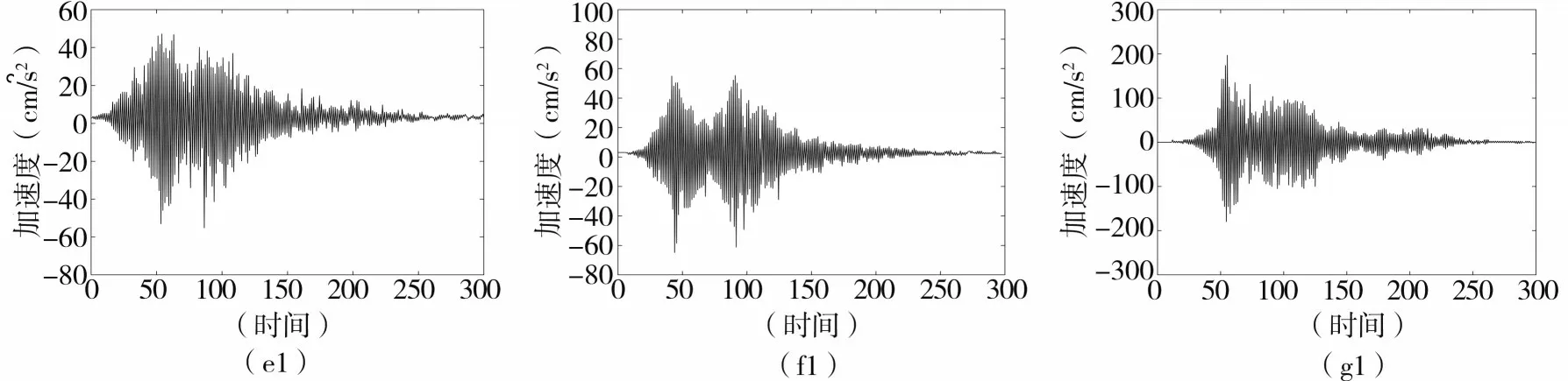
图8 基于MEEMD模型处理的地震动信号Fig.8 Signals processed by MEEMD model

（3）对剩余信号进行4次EMD分解后结果。

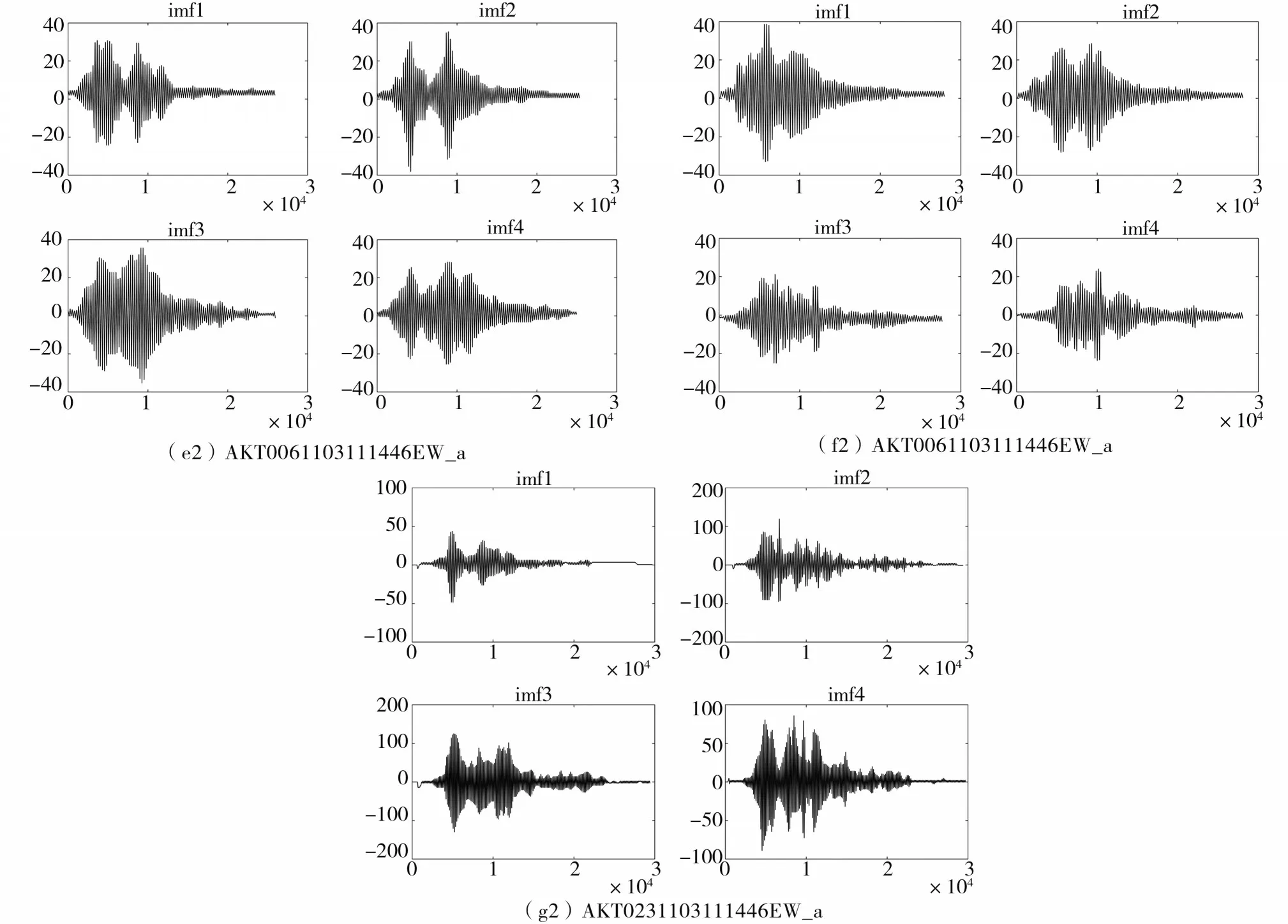
图9 EMD分解后IMFFig.9 The IMF after EMD decomposition

（4）利用VARMA模型将所得的所有IMF仿真还原为地震动信号。

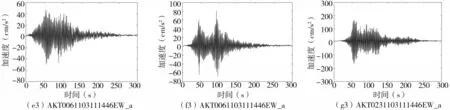
图10 基于VARMA模型还原后地震动信号Fig.10 Earthquake signals restored by the VARMA model

（5）对去噪后的信号进行函数积分运算的连续小波变换，得到位移信号。

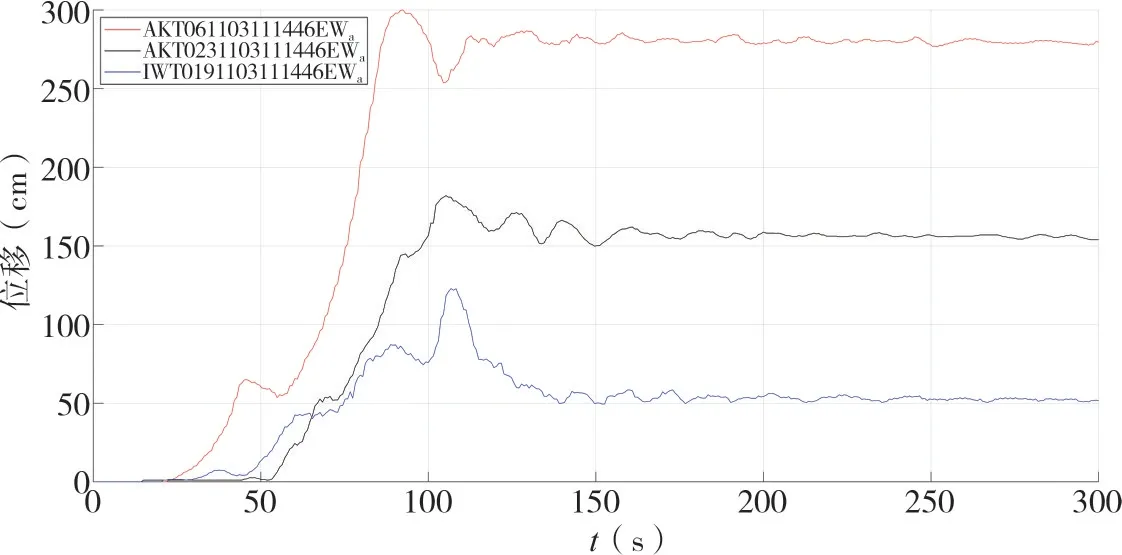
图11 利用本文方法处理得到的位移信号Fig.11 Displacement signals processed by this method

将此结果与GPS台站同震位移对比，相关数据如表1所示。

表1 日本M w 9.0强震记录永久位移识别相对误差Table 1 Relative error of permanent displacement identification in Japan M w9.0 strong motion record

通过对比发现文中方法处理得到的永久位移与GPS台站记录的同震位移之间比较接近，且误差较小，进一步验证了文中方法的正确性和精度较高的优点。

6 结论

基于MEEMD和时变VARMA模型的地震动噪声清除及基线修正方法，在处理工程实测信号时，在去除高频干扰噪声信号的同时完成了基线校正，最终获取有永久地面位移地震动位移信号。优点在于——相对于先验性的小波分解截断法而言，其方法属于一种后验的信号处理方法。不仅无须人为选择小波基函数、小波分解层数、滤波阈值等，减少了人为因素的干扰，降低由此产生的误差，而且继承了EMD直观性、简单性、完备性、近似正交性和良好的自适应性等优点，同时修正了EMD的端点效应、模态混叠等问题。理论上可以应用于任何类型的信号分解，在处理非平稳及非线性数据上，具有明显的优势，其数据处理结果精度高，可满足工程实践的需求。