基于能量法的浮置基础减振系统解析模型

朱龙基，温留汉·黑沙，刘彦辉

（1.广州大学工程抗震研究中心，广东 广州 510405；2.广州大学 广东省地震工程与应用技术重点实验室，广东 广州 510405；3.广州大学工程抗震减震与结构安全教育部重点实验室，广东 广州 510405）

引言

浮置基础减振系统是一种高效的减振技术，常用于大型精密仪器的减振［1-3］。浮置基础减振系统包含设备基础与隔振器2部分，其中隔振器由带有黏滞阻尼器的钢弹簧［4］或带有附加气室的空气弹簧［5］（以下简称空气弹簧）组成，如图1所示［6］。与钢弹簧相比，空气弹簧拥有更低的刚度［7-8］，能更好地满足大型精密仪器在低频微振动工作环境下的减振要求［9］。

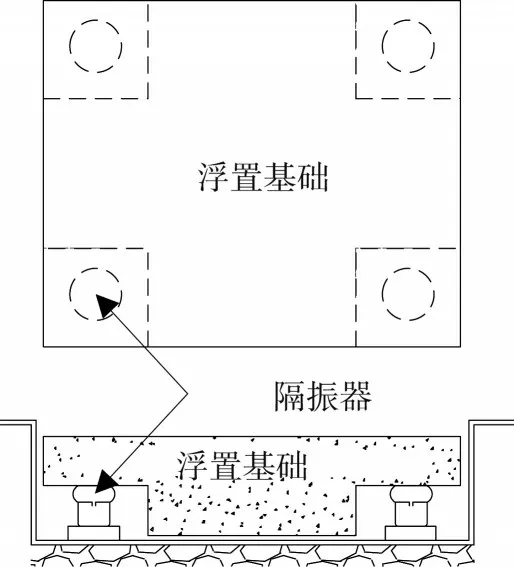
图1 浮置基础减振系统的结构图Fig.1 Structural diagram of floating foundation vibration reduction system

在设计浮置基础减振系统时，需要确定的参数包括浮置基础的尺寸、形状、质量以及空气弹簧的力学性能参数、个数及其布置形式等［10-11］。虽然以有限元方法建立的实体模型比解析模型更准确，但在没有初始设计的情况下建立有限元模型确定设计参数所耗费的工作量过大，使得这项工作不现实［12］。相对而言，解析模型可以更快的帮助设计人员获得较好的初始参数，为有限元建模提供依据［13］。解析模型中，这些参数可以通过以空间矩阵的形式建立浮置基础减振系统的六自由度空间解析模型来确定［14］。

在对隔振系统动力分析的研究中，系统的刚体动力学特性采用平衡方程的矩阵形式［15］。Himelblau和Rubin［16］提出了牛顿-欧拉动态平衡方程，并对正交弹性支承情况下的平面对称问题进行了研究。Angeles［17］给出了振动系统运动方程的矩阵形式，并通过位置矢量的矩阵形式获得了平移、转动、平移-转动下的静态刚度矩阵。Iwan［18］采用等效线性系统方法对隔离系统的非线性弹簧隔振器进行线性化。并在研究中使用了不同的平动自由度和转动自由度，同时选取惯性主轴作为系统的转动自由度，根据坐标系方向选取系统的平移方向。Ibrahim［19］通过解析模型研究了被动隔振系统因大变形、大刚度和几何非线性引起的非线性行为。

以上研究并没有考虑能量在减振系统中转化所激发的动力学特性，文中基于能量法分析得到浮置基础减振系统的动能、势能及阻尼耗散能解析表达式。进一步通过建立运动平衡方程，推导了基于弹性轴向支撑刚体小位移的质量、刚度和阻尼矩阵。在推导质量、刚度和阻尼矩阵的基础上，给出了动力平衡方程以及实模态和复模态的特征分析方程。最后在SAP2000有限元软件中建立了电子束曝光机的浮置基础减振系统的有限元模型，并将解析模型和有限元模型进行了对比分析，讨论了模型求解结果的正确性。

1 浮置基础减振系统的六自由度解析模型

浮置基础减振系统由刚度较大的钢筋混凝土“T”型基础和弹性支撑组成，其中弹性支撑通常用空气弹簧。该减振系统的第七阶为“T”型基础的变形模态，其频率远大于前六阶模态频率，因此可以假设“T”型基础在减振系统工作时为刚体形态。本节利用能量法建立浮置基础减振系统的刚体运动方程，以方便确定浮置基础初始设计参数。计算简图如图2所示，图中k xi表示第i个空气弹簧的x向等效刚度，c xi表示第i个空气弹簧的x向等效阻尼，其他符号类似。首先，通过分析得到刚体的动能T，弹簧势能V和阻尼耗散能Q。然后，假设qk为广义坐标，并将各个能量表达式代入Lagrange运动方程，以矩阵形式表达的系统运动方程。

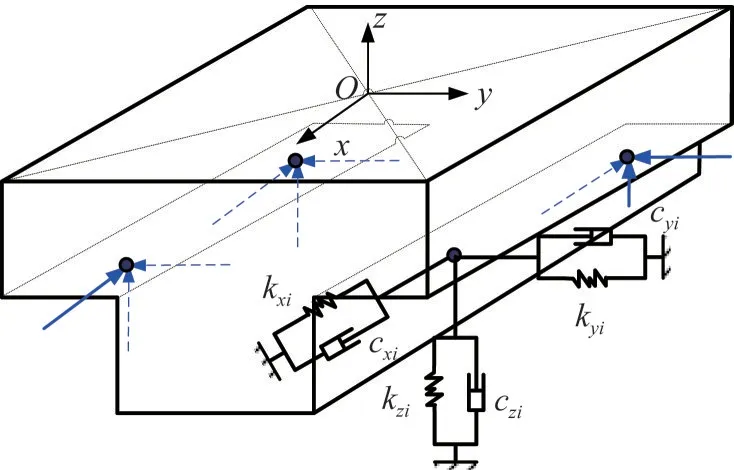
图2 浮置基础的六自由度解析模型计算简图Fig.2 Calculation diagram of analytical model of 6-DOF floating foundation

1.1 系统能量

系统动能：

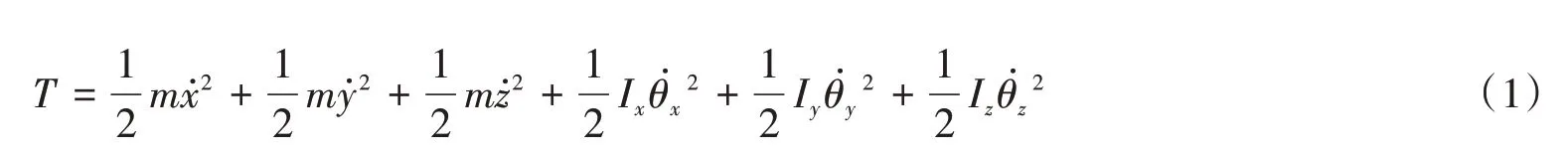
式中：m表示浮置基础质量；Ix、Iy和Iz表示浮置基础绕x、y和z轴的转动惯量；̇、̇和̇表示浮置基础沿x、y和z轴向运动速度̇、和̇表示浮置基础绕x、y和z轴转动角速度。

第i个弹簧的位移：

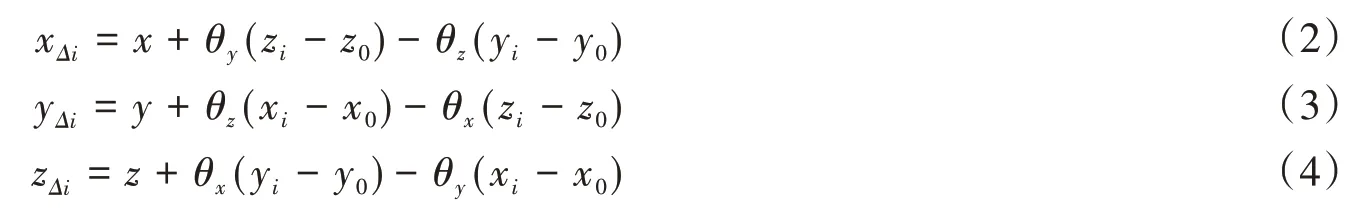
系统弹性变形势能：

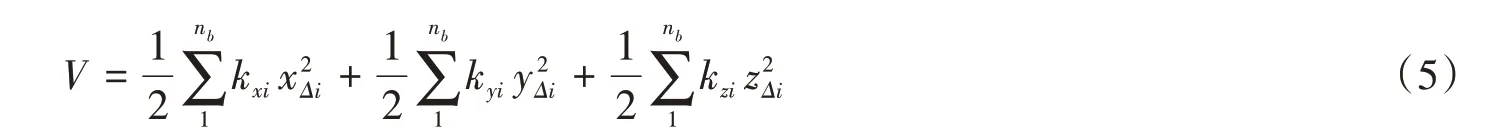
式中：xΔi、yΔi和zΔi表示第i个空气弹簧x、y和z方向的位移；x0、y0和z0表示浮置基础刚心坐标值；θx、θy和θz表示浮置基础绕x、y和z轴转动角度；nb表示隔振器数量。

系统阻尼耗散能：

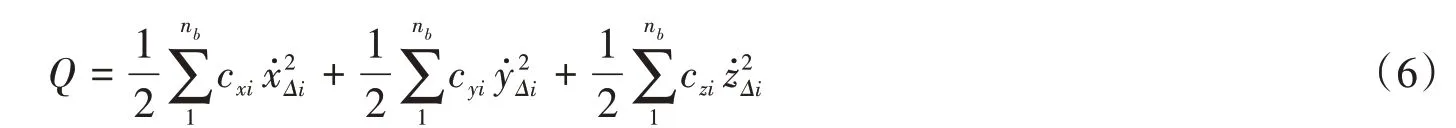
将以上系统能量式（1）～式（6）代入以qk为广义坐标的Lagrange运动方程：

得到各方向运动平衡方程。

1.2 减振系统的质量矩阵，刚度矩阵、阻尼矩阵和力向量

基于各方向运动平衡方程可以得到减振系统的质量矩阵，刚度矩阵、阻尼矩阵和力向量。

质量矩阵：

刚度矩阵：

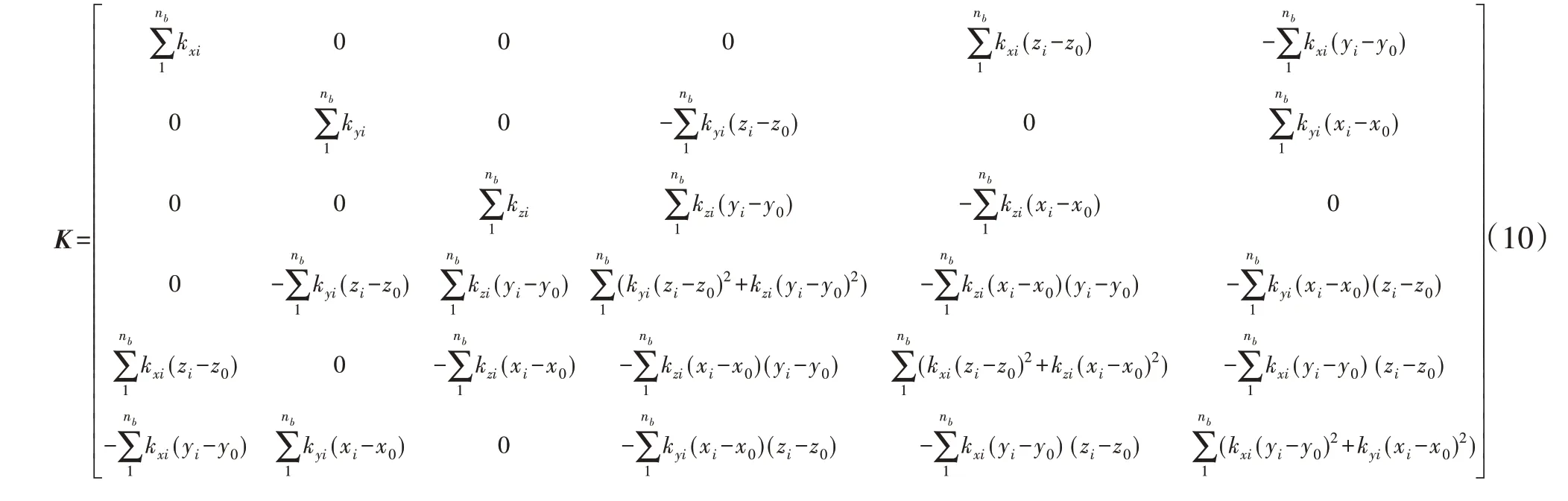
阻尼矩阵：

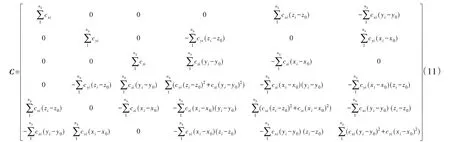
j时刻的力向量：

式中，a x j、a yj和a zj分别表示第j时刻x、y和z方向的浮置基础加速度。

2 特征频率分析

2.1 实模态分析

在工程结构的模态分析中，通常仅由刚度矩阵和质量矩阵构成无阻尼的自由振动的动力方程，由此得到的控制方程为：

采用分离变量法，令u=Qe-iωt，则自由振动特征分析方程为：

式中，QT=[U x,U y,U z,Θx,Θy,Θz,]为模态位移矢量；ω为特征频率。这是减振系统的特征分析方程，对该方程进行求解得到减振系统的6个特征频率。如果质量和刚度均为对称分布时，质量和刚度矩阵变为对称和对角分布，从而得到了6个独立的特征分析方程。

2.2 复模态分析

在实际工程中，浮置基础减振系统为非经典阻尼体系，其阻尼不满足正交条件。因此，文中利用状态空间的方法描述该体系的振动问题［20］，以此进行复模态分析。

式中：I为N维单位向量。为了把系统方程转化为一般特征值问题，引入下面的辅助方程：

则对应式（17）的特征问题为：

由此可得到复特征向量值矩阵为：

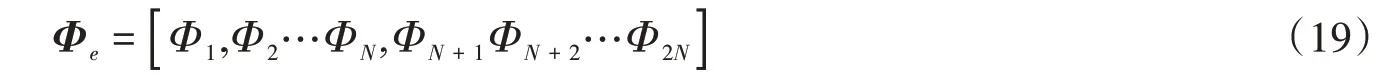
3 浮置基础减振系统分析案例

本节以量子芯片实验室中的电子束曝光机的浮置基础减振系统设计案例为例，对比分析其六自由度解析模型及有限元模型的模态计算结果。该系统的工作环境要求在1.6～16 Hz频域内振动的有效速度小于0.8μm/s，16 Hz及以上频域的有效振动速度小于1 μm/s。所以，减振系统的固有频率需低于该频率值才有减振效果。为了使质心低于空气弹簧平动面以下，以及缩小质心和刚心的距离，将设备基础设计为“T”型截面的钢筋混凝土浮置基础。图3为浮置基础减振系统的示意图，其长11 m，高3 m，质量为293 t。为了减小浮置基础前六阶模态的耦合作用，支撑浮置基础的12个空气弹簧沿着浮置基础长度方向对称布置在两侧的翼缘。

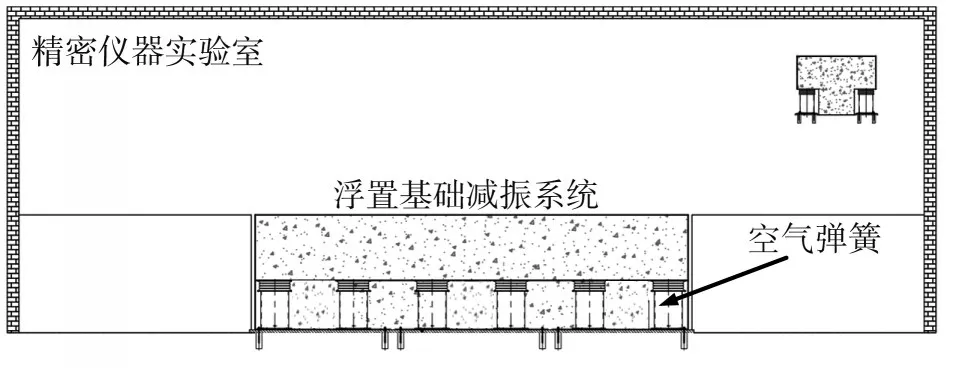
图3 大型精密仪器的浮置基础减振系统Fig.3 Floating foundation vibration reduction system for large precision instrument

3.1 空气弹簧选型

本案例选用的带附加气室空气弹簧物理参数如表1所示。

表1 空气弹簧物理参数Table 1 Physical parameters of air spring

文献［21］中给出空气弹簧刚度和阻尼的计算公式：

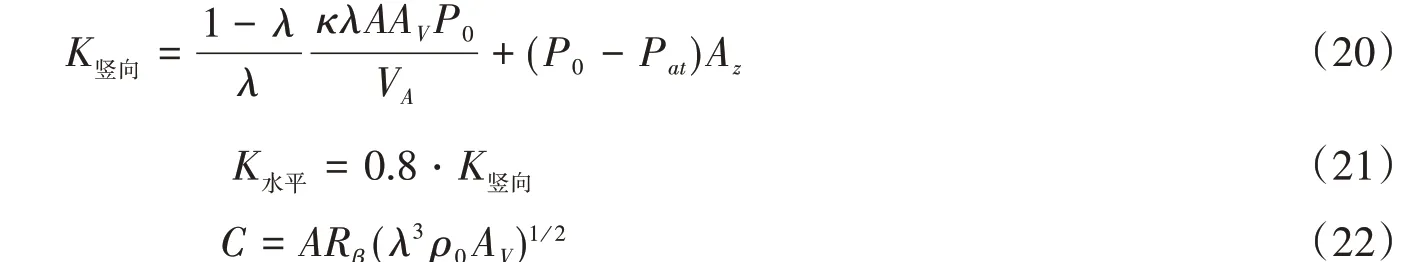
式中：A为主气室在平衡位置处的有效面积；Az为有效面积变化率由dA/dz计算得到；Av为主气室体积变化率；VA为主气室体积；VB为附加气室体积；P0为初始气压；Pat为大气压；ρ0初始气体密度；Rβ为阻尼系数；κ为多变指数，λ=V B/(V A+V B)。

由式（20）～式（22）计算空气弹簧的竖向和水平刚度以及阻尼值如表2所示。

表2 空气弹簧刚度及阻尼Table 2 Stiffness and damping of air spring

3.2 六自由度特征频率分析

由式（8）、式（10）和式（11）形成质量、刚度以及阻尼矩阵：

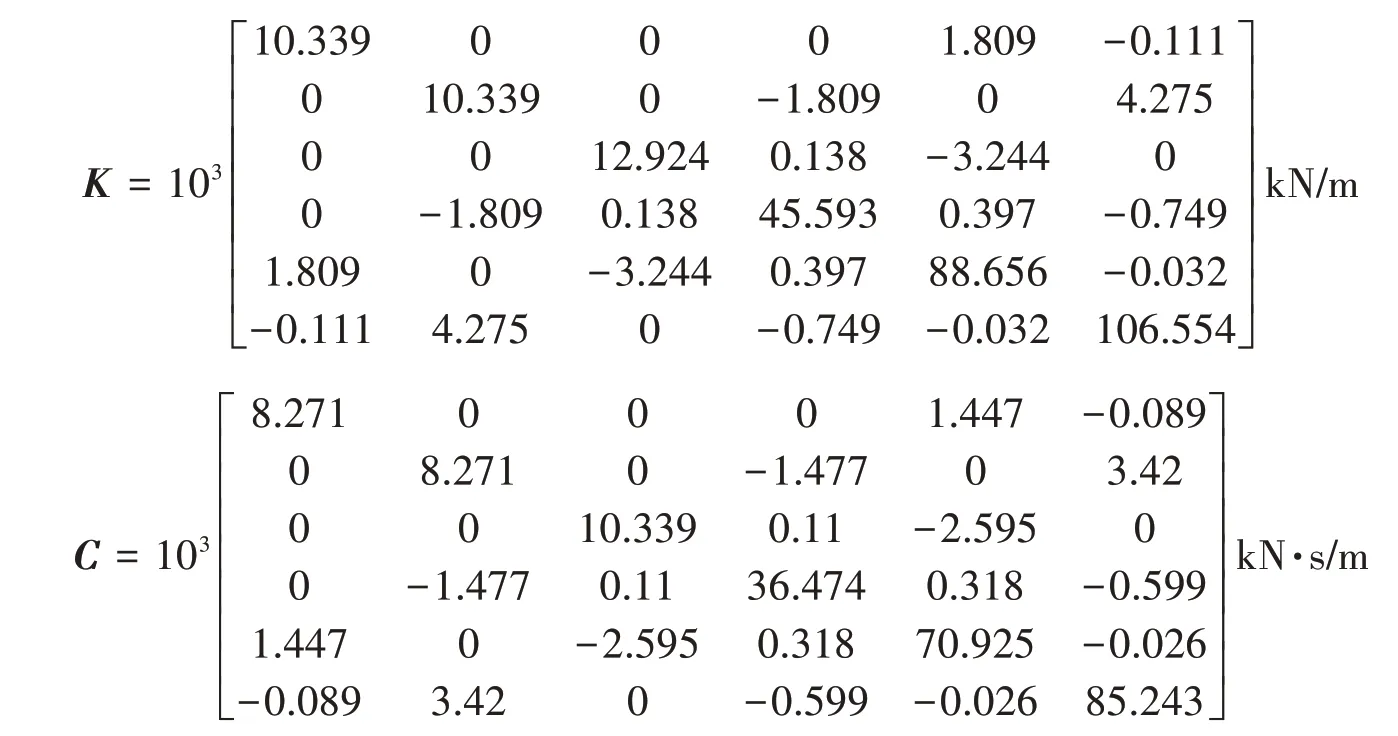
根据式（14）和式（19），计算模态频率如表3所示。

表3 解析模型计算模态及频率Table 3 Modes and frequencies calculated by analytical models

3.3 有限元模型分析

为了验证文中提出的数值解析模型的准确性，本节利用SAP2000有限元分析软件，对同一浮置基础减振系统建模分析。有限元模型中的隔振单元采用线性弹簧单元，并输入空气弹簧的等效刚度和等效阻尼比。有限元模型如图4所示，有限元模型参数如表4所示，计算频率如表5所示。

图4 浮置基础减振系统有限元模型Fig.4 Finite element model of floating foundation vibration reduction systems

表4 浮置基础减振系统有限元模型参数Table 4 Finite element model parameters of floating foundation vibration reduction system

表5 SAP2000计算浮置基础模态频率Table 5 Modal frequency of floating foundation calculated by SAP2000

对比有限元模型和分析计算所得模态及其频率如表6所示。

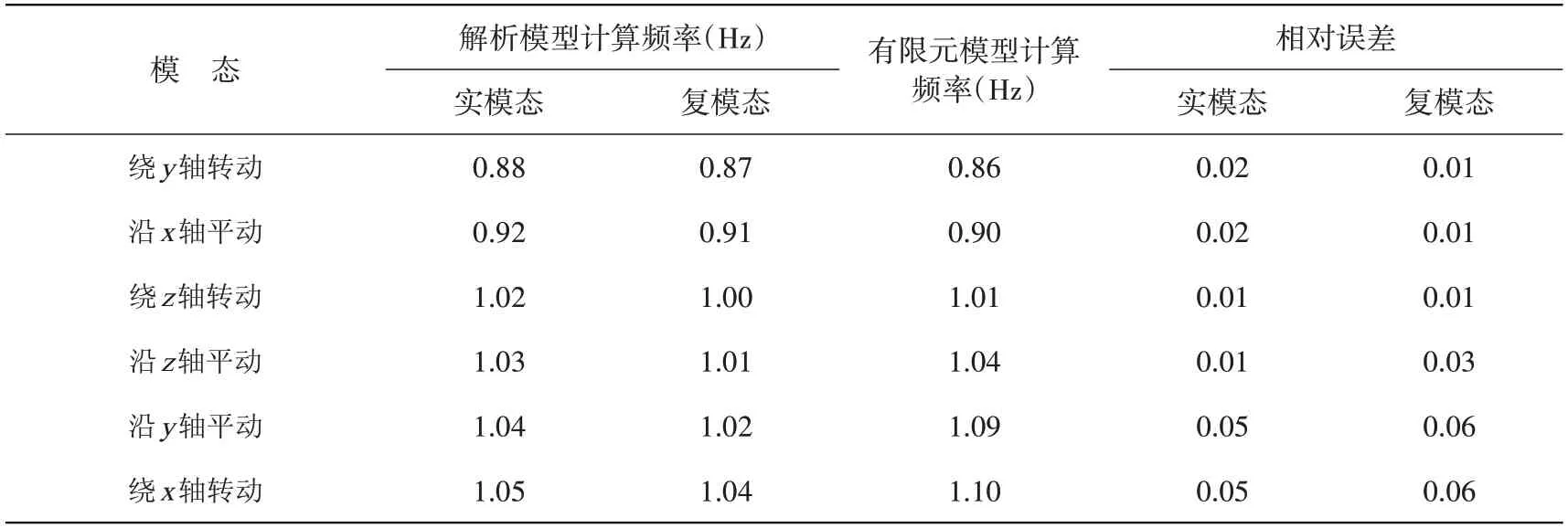
表6 SAP2000与解析模型计算模态对比Table 6 Comparison of calculated modes between SAP2000 and analytical model

由表3及表6可以看出，从解析模型计算所得到的浮置基础振动模态和由SAP2000计算得到的振动模态一致，均由沿3个轴的刚体平动模态和绕3个轴的刚体转动模态组成。SAP2000计算的前六阶模态没有出现浮置基础变形，进一步说明解析模型的六自由度刚体小变形力学的假设是合理的。由表6可以看出，SAP2000与实模态解析模型计算的模态频率相差最小为1%，出现在绕z轴转动和沿z轴平移的第3和第4阶模态，差值最大为5%出现在沿y轴平动和绕x轴转动的第五和第六阶模态。SAP2000与复模态解析模型计算的模态频率相差最小为1%，出现在绕y轴转动、沿x轴平动以及绕z轴转动模态，相差最大6%为沿y轴平动和绕x轴转动模态。由于SAP2000分析模态时采用的是实模态方法，因此解析模型的实模态计算结果比复模态计算结果更接近SAP2000计算结果。

4 结论

文中基于能量法并结合六自由度刚体小变形力学，通过Lagrange运动方程建立了由弹性构件支撑的浮置基础减振系统动力学解析模型，并推导了系统的质量矩阵、刚度矩阵和阻尼矩阵。以一个大型精密仪器的浮置基础减振系统案例，对比分析了其六自由度解析模型及有限元模型的模态计算结果。得到以下结论：

（1）采用文中提出的解析模型和SAP2000有限元模型计算的模态一致，模态频率相对误差在6%以内，验证了文中提出的解析模型的可靠性。

（2）解析模型的实模态计算浮置基础模态频率相对有限元方法计算最大误差为5%，复模态计算的浮置基础模态频率相对误差最大为6%，实模态计算结果更接近有限元方法计算的结果。

（3）文中得到的解析模型可以更快的获得较好的初始参数，为浮置基础减振系统的优化设计提供依据。

附录：

各方向运动平衡方程

x方向：

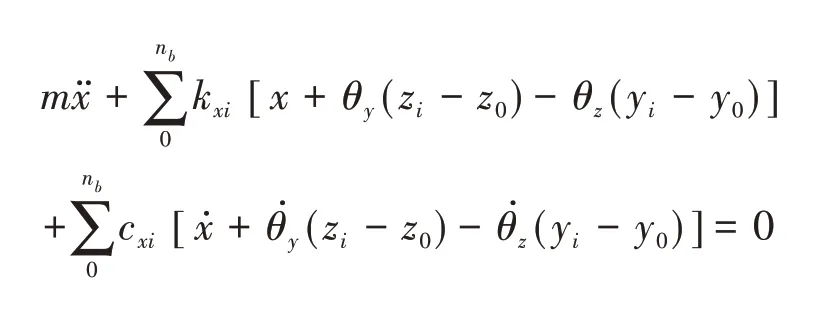
y方向：

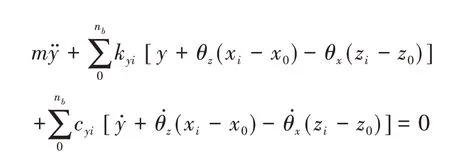
z方向：

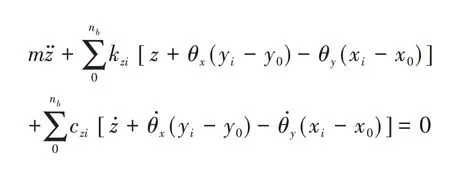
θx方向：

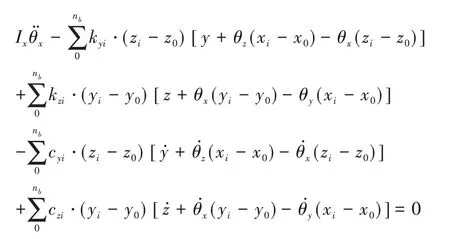
θy方向：

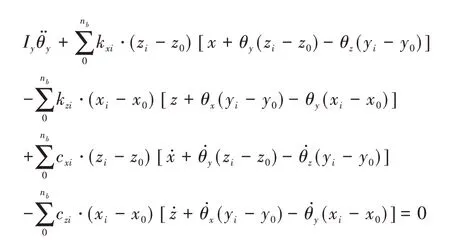
θz方向：