基于振动功率流的周期连续梁损伤识别
2022-05-11吴巧云李雨熹罗和弦荆国强
吴巧云,李雨熹,罗和弦,荆国强,丁 兰
(1.中国地震局工程力学研究所地震工程与工程振动重点实验室,黑龙江哈尔滨 150080;2.地震灾害防治应急管理部重点实验室,黑龙江哈尔滨 150080;3.武汉工程大学土木工程与建筑学院,湖北武汉 430073;4.中国中铁大桥局集团有限公司,湖北武汉 430050;5.中国地质大学(武汉)工程学院,湖北武汉 430074)
引言
在工程结构使用过程中由于受到外部冲击或循环载荷作用,不可避免地会出现损伤从而影响结构性能。为了使结构能够安全高效运营,对结构内部出现损伤的位置和损伤程度进行识别,尤为重要。在实际工程中存在一类由若干重复的子结构首尾相连构成的谐调系统,称为周期结构系统[1]。学者们[2-7]通过对各种类型周期结构的振动和波传播特性进行了系统研究,发现周期结构存在着独特的物理特性,即波在周期结构中传播时交替存在着传播域与衰减域,当波的频率在传播域内时才能有效传播,在衰减域内时则传播受阻。
在过去10多年间已经发展出了相当多的基于振动的损伤识别方法,按照研究方向不同又可进行细分,如动力分析方法[8]、概率方法[9-12]、模态识别方法[13-14]、小波分析方法[15-16]、神经网络方法[17]和信号处理方法[18]等。目前在周期结构损伤识别应用方面多以有限周期结构为研究对象,Yin等[19]针对有限长周期支撑结构提出了基于贝叶斯方法的概率损伤识别方法,通过求解无量纲频率对周期单元刚度变化的敏感性矩阵,获得最可能的损坏结果,并对多跨周期支撑铝梁进行数值模拟和实验研究验证。Yin等[20]还通过贝叶斯方法求解有限长周期性支撑梁结构的传递矩阵,从而识别出周期梁单元跨中的螺栓松动情况。Kang等[21]研究了一有限长周期支撑桥梁的模态定位特征,揭示了模态局部化与支护损伤之间的关系,为基于周期结构的模态局部化特征的桥梁损伤识别提供了理论基础。Koushik[22]提出了一个基于模态斜率和曲率的损伤定位方法,通过分析一个16层的均匀剪切型结构,得到模态曲率会在损伤位置表现出不连续性,且低阶模态对损伤更敏感。闫维明等[23]基于小波包分解频带能量分析和模糊聚类法,提出了一种适合于网格结构的损伤诊断方法,利用2个传感器损伤信息的联合诊断,有效地解决了使用一个传感器无法检测出对称损伤的难题。Apalowo等[24]结合周期结构理论和有限元方法分析不同节点类型下二维层状复合周期结构内局部结构损伤的波相互作用,计算不同损伤类型和结构参数下的波相互作用系数,对损伤的方向和范围进行评估和检测。梁栋等[25]为方便地检测梁桥支座损伤,提出了利用运营桥梁实测模态位移结合其无损状态的模态位移判断支座损伤的高斯曲率模态相关系数法,可准确识别出单支座和多支座损伤的支座损伤位置,具有较强的鲁棒性,可将此方法应用于实际工程中的支座损伤识别。
上述研究多为有限长周期结构下的损伤识别,对于无限长周期结构的损伤识别目前研究相对较少,且对无限长周期结构的研究[26-28]多集中在波的振动与传播特性上,鲜有损伤识别研究。对无限长周期结构的损伤识别,可以使用振动功率流方法从能量角度开展相关研究,与传统基于单一物理量的损伤识别方法不同,振动功率流从能量角度出发即包含有力和速度的幅度,又考虑了它们之间的相位关系,既能表征结构的整体特性,又可反映结构局部物理参数变化[29]。Goyder等[30]提出了功率流的概念,并研究了无限长梁在力和扭矩激振下的近域和远域功率流。Huh等[31]利用振动功率流方法对直梁和方板作用下的裂纹进行了诊断研究,强调仅根据传播功率流位置曲线上出现的突变点即可准确识别裂纹损伤位置。Varghese和Shankar[32-33]采用多目标优化算法,以及功率流平衡技术,对质量-弹簧系统和悬臂梁结构的损伤识别问题进行了研究,结果表明结合振动功率流方法可以达到仅需少量传感器即可提高识别精度的目的。李天匀等[34]结合周期结构理论和点导纳法,分析了损伤等跨连续梁结构的弯曲波运动以及振动功率流的输入和传播特性,为基于振动功率流方法的周期结构损伤识别提供了思路。从以上研究可以看出基于振动功率流的损伤识别方法已经应用到了简单的悬臂梁、板等结构,在无限长周期连续梁结构上仍有相当大的研究空间。
文中以无限长周期连续梁结构为研究对象,以振动功率流为研究方法,以裂纹作为损伤形式,使用周期结构传播理论和振动功率流方法分别计算健康与损伤状况下连续梁中波在结构中传播时产生的传播功率流与输入功率流。通过分析振动功率流与损伤位置和损伤程度的关系,证实了在无限长周期连续梁中使用振动功率流方法进行损伤识别的可行性。
1 周期连续梁物理模型
1.1 Euler-Bernoulli梁自由振动的解析解
支撑在刚性支座上的矩形截面无限长周期连续梁示意图如图1所示,其任意两相邻支座间均为等截面的Euler-Bernoulli梁,每两跨之间通过抗弯弹簧进行耦合,其自由振动微分方程为

式中:E为材料杨氏模量;I为截面惯性矩;ρ为材料密度;A为横截面面积;y(x,t)为梁的横向位移。考虑梁的简谐运动,

式(1)可化简为:

引入状态向量V(x),其表达式如下:

式中ϕ(x)、θ(x)、M(x)、Q(x)分别表示x截面处的挠度、转角、弯矩和剪力。
可以得到方程(3)的解析解表达式如下,其中T(x)表示Euler梁的迁移矩阵:

其中

1.2 裂纹弹簧模型
定义周期连续梁中的损伤为裂纹形式,图2中表示等截面矩形Euler-Bernoulli梁中的裂纹模型示意图,将裂纹损伤描述为一柔度弹簧。

图2 弯曲弹簧模型Fig.2 Bending spring model
使用Dimarogonas等[35]的弯曲弹簧理论,得到裂纹的柔度c为:

式中表示裂纹的相对深度。
在裂纹左右两端各个物理量挠度ϕ、转角θ、弯矩M和剪力Q之间的关系如下,

式中,下标l、r表示裂纹处的左右截面,cE Iθl表示裂纹处简化为弯曲弹簧而产生的转角。将式(10)表示为矩阵形式,

或表示为,

式中:V l(x0)为裂纹左侧的状态向量;V r(x0)为裂纹右侧的状态向量;T0表示裂纹处的迁移矩阵。
1.3 周期连续梁的传播常数
如图1所示,当在梁上给定一简谐力激励F=F0eiωt时,从激励位置开始在整个梁上产生简谐波。当波在无穷周期结构中传播时,其幅值以指数eμ的形式衰减,该指数常数μ被称为传播常数,μ=η+iβ,其中η表示波幅的衰减,β表示相位差。在MEAD[2]的研究中,给出周期连续梁的传播常数表达式与Euler梁结构阻抗有如下关系:

式中,αab(a,b=0或x或l)表示单跨梁的1导纳函数,第一个下标表示梁上a处的响应,第二个下标表示梁在b处受到单位简谐激励。文中0表示单跨梁左支座处,l处表示单跨梁右支座处;如果下标上有撇表示与转角或弯矩有关,如果下标上没撇表示与位移或剪力有关。
2 周期连续梁的功率流推导
2.1 健康周期连续梁的功率流
图3表示简谐激励下周期连续梁的受力分布,集中激励荷载位于第n跨梁。假设A、B和C、D支座分别为第n-1跨和n+1跨支座,A、B、C、D支座处弯矩分别为M(0)eμ、M(0)、M(l)、M(l)eμ。

图3 无限周期连续梁力学模型Fig.3 Mechanical model of infinite period continuous beam
对于图3中的周期连续梁,第n跨梁存在如下关系式:
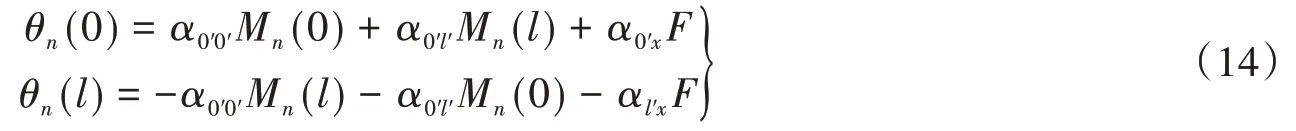
两端支座处的连续条件为[36],

式中α∞表示半无限周期梁末端的导纳函数为,

式中,μ为传播常数。
联立方程可得:

式中H1和H2为关于传播常数μ和激励位置x的函数。
当梁在单频激励下振动时,根据振动功率流的定义[35],计算由激励处传播到梁两端支座处的功率流为

式中:“*”表示共轭复数;Re表示取实部;β表示波的相位差。
在不考虑阻尼影响时健康连续周期梁的输入功率流为:

2.2 含裂纹周期连续梁的功率流
第n跨损伤梁单元模型如图4所示,图中x0表示损伤位置,在激励作用位置x f处有连续条件:
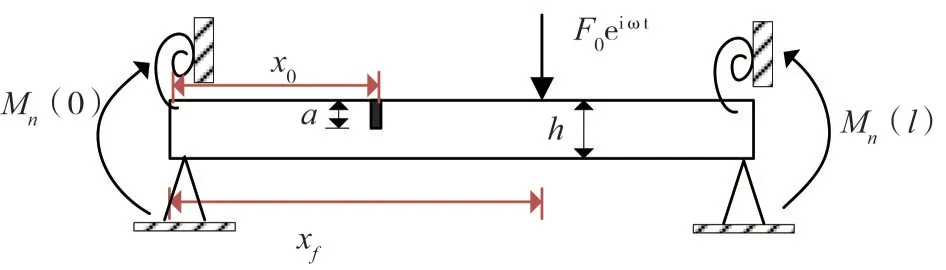
图4 第n跨损伤梁单元模型Fig.4 Element model of damaged beam in the No.n span

或表示为

式中V l(x f),V r(x f)分别表示施加激励处左右截面的状态向量;V(F0)表示激励矩阵。
对图4中的第n跨损伤梁:

式中V n(0),V n(l)分别表示第n跨梁左右支座处的状态向量。
代入边界条件:

联立方程(22)与(23)可以解得:

式中H3和H4为关于传播常数μ、激励位置x f、损伤位置x0和损伤程度aˉ的函数。
根据振动功率流的定义,可以得到在传播域中传递到左右支座的功率流为:

式中,上标D表示为含裂纹的梁中的功率流。
同样,在不考虑阻尼的含裂纹连续周期梁的输入功率流为:

3 数值分析
本节分析一横截面尺寸0.1 m×0.1 m,弹性模量E=2.1×1011N/m2,密度ρ=7 780 kg/m3的单跨长度l0=1 m的无限长周期连续梁的输入功率流特性,并进行损伤识别研究。
3.1 周期连续梁输入功率流特性
根据式(19)和式(26),代入不同的损伤程度和损伤位置,得到算例模型的输入功率流曲线如图5和图6所示的输入功率流曲线。图中横坐标为无量纲频率λL,纵坐标为无量纲功率log10PE IρA/F2L,P表示输入功率流,F表示激励幅值,L表示单跨梁的长度,x f l0表示相对激励位置,aˉ表示裂纹相对深度,x0l0表示相对损伤位置。
由图5能够看出波动在健康周期连续梁的传播时存在带隙特性,在无量纲频率为(3.14,4.73)、(6.28,7.85)、(9.42,10.99)、(12.56,14.14)频率区间时,结构处于传播域,振动功率流不为零。在其他频率范围内结构则处于衰减域中,功率流为零。可以发现第一传播域的上、下边界点即界频率的大小与单跨梁简支、固支时的一阶无量纲固有频率相等,第二传播域界频率对应二阶固有频率,以此类推。图5中可以看出,在第一传播域中,上、下界频率处的输入功率流趋近无穷大,但是随着激励位置越靠近梁的中部,输入功率流的值越大,在第二传播域内该跨梁的振动模态以单跨梁在简支、固支时的二阶振动模态为主,越靠近梁中部振动位移越小,因此激励位置位于跨中时的功率流最小,激励相对位置为x f/l0=0.2附近时跨时输入功率流最大。在第三传播域内该跨梁的振动模态以单跨梁在简支、固支时的三阶振动模态为主,当激励相对位置为x f/l0=0.3附近时,位移最小,故输入功率流相对较小,激励位于跨中时位移大,输入功率流也大。在第四传播域内,励位置位于跨中时,位移最小功率流最小,在上下界频率处时位移为零,功率流也为零,激励相对位置为x f/l0=0.1和x f/l0=0.4附近时,振动位移较大,输入功率流也相对较大。
通过图5的分析可以知道周期连续梁在各个传播域中的运动模态和单跨梁在固支、简支时的振动模态保持一致,特别是激励位于跨中时,由于单跨梁的各阶振型在跨中处表现出极值、零的交替变化规律,对应着的输入功率流在不同传播域中也表现出奇数传播域大、偶数传播域小的变化规律,因此下文均选取激励位于跨中的情况进行损伤梁振动功率流的研究。

图5 健康周期连续梁输入功率流曲线Fig.5 Input power flow curve of healthy period continuous beam
图6给出在梁中点处(x f/l0=0.5)施加激励时,不同损伤位置和损伤程度下损伤连续梁的输入功率流曲线。图6(a)为损伤程度一定,损伤位置改变时的功率流变化曲线;图6(b)为损伤位置一定,损伤程度改变时的功率流变化曲线,aˉ表示裂纹相对深度,x f/l0表示相对损伤位置。

图6 损伤连续梁输入功率流曲线(跨中激励)Fig.6 Input power flow curve of damaged continuous beam(mid span excitation)
从图6可以看出由于裂纹的出现,在第一、三传播域内上界频率处的功率流P Din不在趋于无穷,因此推断裂纹的产生改变了梁单元的振动模态,不在以单跨梁两端简支、固支时对应阶数的模态振型为主,而在二、四传播域则保持了单跨梁在两端简支、固支时的振动规律。由图6(a)可知在固定损伤程度时,第一、二传播域内损伤越靠近跨中,输入功率流越小;第三、四传播域内损伤越靠近支座,输入功率流越小。由图6(b)可知固定损伤程度时,第一、三传播域内损伤程度越大,输入功率流越小;在第二、四传播域内损伤越大,输入功率流越大。
图7给出了当激励位置位移梁跨中时,不同损伤情况下传播到梁左端支座处的功率流与输入功率流的比值Ptr0/Pin,其中纵坐标为0.5的直线表示当梁未发生损伤时由激励位置输入梁中的功率流均匀向梁两端传播。图7(a)表示损伤程度固定,不同损伤位置情况下,功率流向梁两端传播的分布规律,第一传播域内传播到梁左端的功率流占总功率流的分布曲线轮廓不一、相互交叠,不易判断出损伤位置的区别。图7(b)~(d)表示在不同损伤程度下,功率流向梁两端传播的分布规律,在第一传播域中传递到梁左端的功率流随着损伤程度的加深而增大,在第四传播域中传递到左端的功率流随着损伤程度的加深而减小,在第二、三传播域中根据损伤位置的不同传递到梁左端的功率流大小规律不一,总体上损伤程度越小功率流分布曲线越靠近0.5直线,另外还可看出不同损伤程度下的功率流分布曲线轮廓线一致,分层良好互不干扰,表明了功率流分布曲线对损伤程度更加敏感,以此特性即可优先判断出损伤程度。

图7 损伤连续梁传播功率流分布曲线Fig.7 Power flow distribution curve of damaged continuous beam
3.2 基于归一化输入功率流的周期连续梁损伤识别
通过前一节的分析,损伤的发生改变了梁的振动模态,周期连续梁的功率流特性与损伤的位置和程度有密切的联系。将梁存在损伤时的输入功率流与健康时的输入功率流的比值定义为归一化输入功率流,在不同激励频率下归一化输入功率流与损伤位置和损伤程度之间的关系如图8所示,图8中给定的4个激励频率,分别位于不同的传播域内,以此代表四阶不同的传播域。
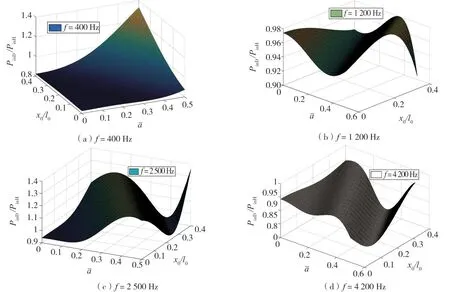
图8 损伤连续梁各传播域内归一化输入功率流三维曲线Fig.8 Three dimensional curves of normalized input power flow in each propagation domain of damaged continuous beam
图8表示了在各阶传播域内的归一化输入功率流的三维曲面,可以看出在不同频率下归一化输入功率流曲面都呈现出波浪状的变化规律,因此同一个归一化输入功率流的值对应的损伤位置和损伤程度不是唯一确定的,要进行损伤识别还要对图8进行处理,将图8中的三维曲面投影到垂直于x0/l0轴的平面上,得到不同损伤位置下的归一化功率流曲线的轮廓线,如图9所示。

图9 损伤周期连续梁各传播域内归一化输入功率流曲线Fig.9 Normalized input power flow curve in each propagation domain of damage period continuous beam
图9中4个频率值分别位于不同的传播域中,代表前四阶传播域。图9表示了各个传播域中不同损伤程度和损伤位置下的归一化输入功率流曲线轮廓图,在前3个传播域中不同损伤程度和损伤位置下的归一化输入功率流曲线轮廓互不干扰,在确定归一化输入功率流的值和损伤程度的情况下可以快速且唯一的确定损伤位置,而在第四传播域中归一化输入功率流曲线则存在交叉现象,因此相同归一化输入功率流和损伤程度的情况下可能得到不同的损伤位置,将对识别造成干扰,因此损伤识别过程不宜在高阶传播域内进行。
基于上述表达的振动功率流传播特性,得出一套基于振动功率流的周期梁结构损伤识别方法,如图10所示。
从图10中可知要完成损伤识别需要进行3步:(1)确定周期结构的能带特性以得到传播域与衰减域的范围;(2)比较功率流分布曲线轮廓图确定损伤程度;(3)绘制归一化输入功率流曲线轮廓,在低阶传播域中确定损伤位置。

图10 基于振动功率流的周期连续梁损伤识别步骤Fig.10 Damage identification steps of periodic continuous beam based on vibration power flow
4 结论
文中主要研究了在某跨中施加激励时周期连续梁的振动功率流特性。由分析可知,在不同传播域中,振动输入功率流呈现出不同的特性。周期连续梁的各个传播域的上、下界频率和单跨梁在两端简支、固支时的固有频率一一对应,当周期梁未发生损伤时,在各个传播域中的振动模态以单跨梁在固支、简支时的振动模态为主,因此不同传播域内,在不同位置激励时的输入功率流大小与相对应阶数的振型的大小保持一致。特别是激励位于跨中时,由于单跨梁的各阶振型在跨中处表现出极值、零的交替变化规律,对应着的输入功率流在不同传播域中也表现出奇数传播域大、偶数传播域小的变化规律。由于损伤的发生改变了梁的振动模态,在跨中激励时第一、三传播域中的输入功率发生的逆转。
通过分析功率流的分布曲线可知在损伤位置固定不同损伤程度情况下,损伤程度越小功率流分布曲线越靠近0.5直线,另外不同损伤程度下的功率流分布曲线轮廓线一致,分层良好互不干扰,可作为判断损伤程度的依据。通过绘制归一化输入功率流三维曲面,进而得到各个传播域内不同损伤情况下的归一化输入功率流曲线轮廓图,在低阶传播域中归一化输入功率流曲线轮廓互不干扰,在确定损伤程度的情况下可唯一确定损伤位置。最后按照确定周期结构传播域范围;绘制功率流分布曲线轮廓图确定损伤程度;绘制低阶传播域下的归一化输入功率流曲线轮廓确定损伤位置的步骤完成整个损伤识别过程。
附录:
导纳函数:

其中F函数由Bishop[35]给出:
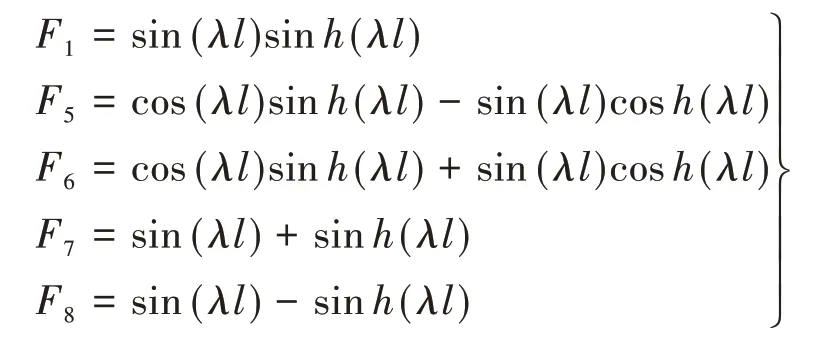
带入导纳函数可得:

