基于聚类分析方法的多功能雷达工作模式识别*

翟龙军 但 波 宋伟健 高 山

（海军航空大学 烟台 264001）

1 引言

为了应对复杂战场环境，多功能雷达（Multifunction Radar，MFR）设计有多种工作模式，通常包含搜索工作模式、监视工作模式、跟踪工作模式和制导工作模式等[1～3]。针对MFR工作模式的识别作为侦察系统中的关键一环在现代电子战有着至关重要的作用，并对后续实现雷达的威胁估计、行为意图推理、自适应雷达对抗等重要环节提供了基础，其水平高低直接决定了电子情报侦察、电子支援侦察、电子对抗、引导攻击等关键军事行动的有效性[4～5]。雷达工作模式识别具体是指在对截获信号识别后，进一步根据其数据特征和信号规律通过分类识别的方法获得其工作模式。本文利用人工智能的相关算法，通过对雷达侦察分选得到的辐射源描述字（EDW）[6～7]进行聚类分析得到MFR工作模式的分类结果。

2 MFR工作模式简介

为实现不同的功能用途和实际应用场景，MFR分别使用对应不同的工作模式，其中主要包括搜索模式、监视模式、跟踪模式和制导模式。

根据MFR在实际使用中的情况，从侦察分选得到的辐射源描述字（EDW）的重复周期、中心频率和脉冲宽度三个方面进行简单的数据处理后对上述四种雷达工作模式进行描述。各种雷达工作模式的统计数据如表1所示。

表1 雷达工作模式的参数统计数据

本文将对上述四种工作模式下雷达信号的数据使用K-means聚类方法进行识别。

3 算法介绍与分析

3.1 K-means聚类算法

K-means聚类算法又称为K均值算法，是无监督的人工智能算法领域最常用、最为经典的一种聚类算法，具有下述方面的优势，即伸缩性强、易于收敛、实现方式简单、可靠性高、好的聚类效果等[8～12]。其基本步骤如下。

1）初始化：从数据对象个数为m的数据样本集X中随机选择K个数据对象作为K个簇类初始的聚类中心C={C1，C2，…，CK}；

2）距离计算：对Χ中的Χi，确定其与聚类中心Cj之间所对应的距离Dij，一般而言，应用的是欧氏距离；

3）数据对象聚类：对相邻数据进行比较，将其归至与之距离最短的聚类中心Cj簇；

4）确定评价准则函数E1值；

5）更新聚类中心：对各簇聚类中心进行更新，使其转变成当前族类中所有数据对象的平均值；

6）重新计算更新聚类中心后的评价准则函数E2；

7）迭代判断：对E1、E2的值进行比较，倘若两者不一致，重复上述步骤，直至E1、E2的值一致，说明达到收敛，完成聚类，并获得了K个簇类。

由上述算法步骤可以得到K-means聚类算法的流程图如图1所示。

图1 K-means聚类算法流程图

3.2 算法合理性分析

本文针对雷达四种不同工作模式进行识别。在相同工作模式下，雷达信号具有较高的相似程度，而在不同工作模式下，雷达信号间的特征差异较大。这样的工作模式特征使得雷达信号的数据样本集呈现凸状特性，恰好与K-means聚类算法的优点匹配。此外，雷达工作模式种类是明确的，解决了K-means聚类算法中簇类个数预设问题。而且雷达每个工作模式有相对明确的参数划分，可以利用先验知识对四个聚类中心实现较优的初始化。

4 实验结果

4.1 实验数据集

在本次研究中，共分析了四种雷达工作模式。因此，在使用K-means聚类算法进行探究时，簇类个数K=4。根据表1中雷达工作模式的EDW的参数范围，每个工作模式随机各生成500组，共计2000组数据。

4.2 预处理及实验过程

充分考虑到雷达工作模式的先验信息，在选取各个簇类的聚类中心时，聚类中心初值采用的是各参数均值。其中，脉冲宽度参数初值确定为重复周期与脉冲占空比均值之积。表2展示的是最终确定的初值情况。

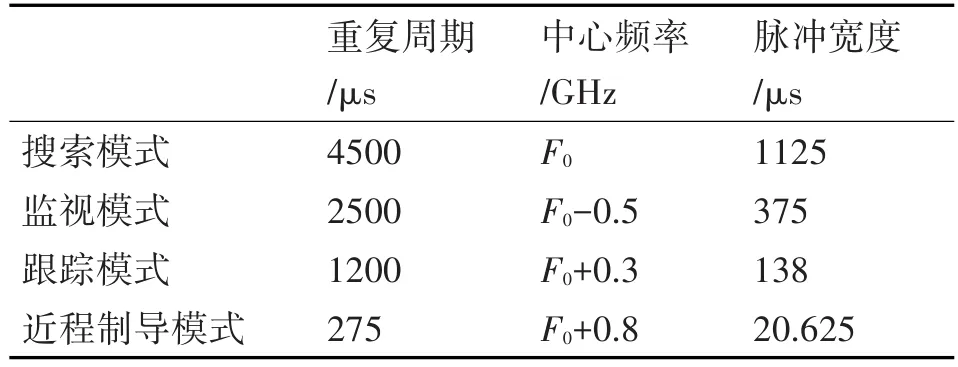
表2 雷达4种工作模式聚类中心初始值

对于雷达在各维度下的特性，可借助于以下参数来确定：脉冲宽度、重复周期、中心频率。因为上述三个参数所对应的物理含义存在较大差异，所以在使用各参数的欧式距离作为相似性度量时，需要在三个参数各自维度上分别做归一化数据处理，方可用数据对象与聚类中心的欧式距离来度量偏离情况。

本文对上述随机生成的含有4000组数据样本的数据集使用基于EDW中的重复周期、中心频率和脉冲宽度三个方面的K-means聚类算法划分。同时，将该算法终止条件确定如下：其一，迭代次数达到100000次；其二，聚类中心没有发生变化。只要满足上述两个条件中的一个，便可终止算法。

4.3 实验结果及分析

实验对四种雷达工作模式各500组数据对象，在上述三个参数的基础上进行算法划分，最终结果详见表3。图2展示的是聚类划分以后所获得的散点图，对于正确、错误的数据分别使用“o”、“x”表示，“☆”指代的是聚类中心。同时将原始数据绘制在该图中，并用“*”表示。实验中选取的搜索模式、监视模式、跟踪模式、制导模式分别对应黑色、红色、绿色和蓝色这4种颜色。

图2 整组2000个数据对象基于三个参数的K-means聚类算法划分的原始数据和划分结果散点图

观察表3可以发现，经过K-means聚类算法划分后，在搜索、监视、跟踪以及制导四种模式识别方面，所对应的准确率显著提升，达到了97%。虽然在生成数据集的过程中引入了噪声因素，但是对于搜索、监视、跟踪模式，借助于该算法仍能够对其进行有效划分。

制导模式识别的准确率能够达到94.8%，这意味着在使用K-means聚类算法时，难以实现对少量数据的有效识别。通过对此部分数据进一步分析发现，均将其误识别为跟踪模式。通过对制导与跟踪模式下雷达参数设置情况进行探究可知，两者在脉冲宽度、重复周期以及中心频率均存在相应重叠。正是由于该原因，进而导致制导模式识别正确率较低。

5 结语

经过K-means聚类算法的理论分析和实验验证不难得出K-means聚类算法能够对MFR的多种工作模式实现正确划分。论文实验中四种工作模式均为固定重频信号，实际雷达工作情况更加复杂，其重复频率往往不是固定重频，针对此类复杂波形需要进行更加深入的研究并可能需要引入基于深度学习的方法提高识别概率。工程实现时，算法可以在基于DSP或FPGA的硬件处理平台上实现，以提高算法的执行效率。