基于多传感器信息融合的扩展目标GIW-PHD跟踪算法
2022-05-11李鹏张骏男王杰陈澄邱骏达由从哲
李鹏 张骏男 王杰 陈澄 邱骏达 由从哲

[摘 要]针对扩展目标跟踪和形状估计问题,单个传感器探测数据并不够精准,需要多个传感器联合探测。然而,现有扩展目标跟踪算法对多传感器情况未做讨论。因此,文章提出1种基于传感器探测角度的三维扩展目标量测模型和多传感器信息融合算法,并将其应用到GIW-PHD算法中。仿真实验证明了提出的算法运动状态和形状估计能力优于现有算法。
[关键词]扩展目标; GIW-PHD; 多传感器
[中图分类号]TP212 [文献标志码]A [文章编号]2095–6487(2022)03–0–03
Extended Target GIW-PHD Tracking Algorithm Based
on Multi-sensor Information Fusion
Li Peng,Zhang Jun-nan,Wang Jie,Chen Cheng,Qiu Jun-da,You Cong-zhe
[Abstract]For the problem of extended target tracking and shape estimation, the detection data of a single sensor is not accurate enough, and multiple sensors need to be jointly detected. However, existing extended target tracking algorithms have not discussed the multi-sensor case. Therefore, this paper proposes a 3D extended target measurement model and multi-sensor information fusion algorithm based on sensor detection angle, and applies it to the GIW-PHD algorithm. Simulation experiments show that the proposed algorithm has better motion state and shape estimation ability than existing algorithms.
[Keywords]extended target, GIW-PHD, multi-sensor
1 概述
傳统的目标跟踪算法认为单个目标每帧仅产生1个量测。然而,随着传感器精度的提高,单个目标可能占用传感器的多个分辨单元,因此单个目标每帧可能产生多个量测,称这样的目标为扩展目标[1](Extened object)。针对扩展目标跟踪问题,Koch等人提出了基于随机矩阵的扩展目标跟踪算法[2-4]。RMF利用卡尔曼滤波估计扩展目标的质心运动状态,认为目标量测的协方差矩阵服从逆威沙特分布,从而估计椭圆目标的形状信息。
RMF仅能估计单扩展目标的状态,因此,Granström等人基于多扩展目标PHD跟踪滤波框架[5]和RMF,提出了Gaussian Inverse Wishart PHD算法[6](GIW-PHD),能够在杂波环境下跟踪并估计多椭圆扩展目标的状态。文献[7-9]给出了基于PHD的其它跟踪算法。然而,GIW-PHD算法没有在多传感器情况下做相关讨论,真实场景中,单个传感器仅能从1个角度对目标进行探测,因此不能提供完整的目标状态数据。
针对上述问题,文章提出1种基于多传感器信息融合的GIW-PHD算法。①提出一种三维扩展目标模型,根据传感器可视的目标表面区域随机产生量测源,量测源加噪声后形成量测;②提出一种多传感器量测信息融合算法,计算量测是重复数据的概率并赋权重,从而提高目标质心和形状的估计精度;③将多传感器信息融合数据在GIW-PHD中应用。
2 量测模型
假设1:量测是由目标体上的量测源加噪声后产生。
令表示目标形状方程,表示量测源坐标向量,D表示目标的形状参数集合,则根据假设1有
(1)
其中,z表示量测坐标向量,w表示量测噪声向量。利用目标形状方程产生某量测源时,若要判断某传感器能否观测到该量测源,可令s(h)表示第h个传感器的坐标向量,表示过和s(h)的直线方程,则有方程
(2)
该方程可解,令表示式(2)的解集。因为解集在直线上,传感器在坐标s(h)仅能看到解集中离s(h)最近的点,因此判断传感器能否观测到有
(3)
(4)
c(·)表示观测约束,当为true表示量测源可被传感器观测到,当为false表示不可被观测到,因此式(1)中的定义域可被约束为
(5)
此时,只要知道D服从的分布,例如均匀分布,就可以通过该分布随机产生D得到,并通过式(5)约束筛选合适数量可被传感器观测的,最后通过式(1)产生量测,则量测建模完成。
3 椭球量测建模
目标形状为椭球时,形状方程可用椭球标准参数方程和坐标旋转矩阵表示
(6)
(7)
(8)
(9)
(10)
(11)
其中,A是椭球标准参数方程向量,且β∈(0,π),γ∈(0,2π);U1,U2,U3是对应x,y,z轴的旋转矩阵。方程中a,b,c,ω1,ω2,ω3为预设固定形状参数,该组参数变化导致椭球形状变化;α,β为随机变量,通过随机的产生该组值随机产生。令=[x0,y0,z0]T是α0,β0确定的某量测源坐标向量,s(i)=[xs,ys,zs]T是某传感器坐标向量,则式(2)被确定为
(12)
式(12)是关于α,β的方程可被求解,然后通过式(3)—(5)计算是否符合约束。
4 MS-GIW-PHD的实现
基于上1节模型,每个传感器从自身角度都会探测目标的1个侧面。然而,所有传感器探测得到的目标侧面并非独立的,而是存在重叠部分,若不对这些重复数据进行处理,则会直接影响目标的状态估计。
因此令k时刻量测表示为
, (13)
其中,Zk表示所有传感器产生的量测,表示传感器s(h)产生的量测,表示传感器s(h)产生的第个量测。令量测噪声服从线性高斯分布,则根据式(1)量测服从的分布为
(14)
其中,表示第h个传感器探测目标产生量测服从的分布,N(·)表示高斯分布,Rk量测噪声协方差矩阵。由于式(14)求解困难,采用高斯拟合法有
(15)
其中,表示目标在第h个传感器产生量测的数量,Xk|k-1表示目标的先验协方差。此时,设共有n个传感器,定义第h个传感器第个量测的权重为
(16)
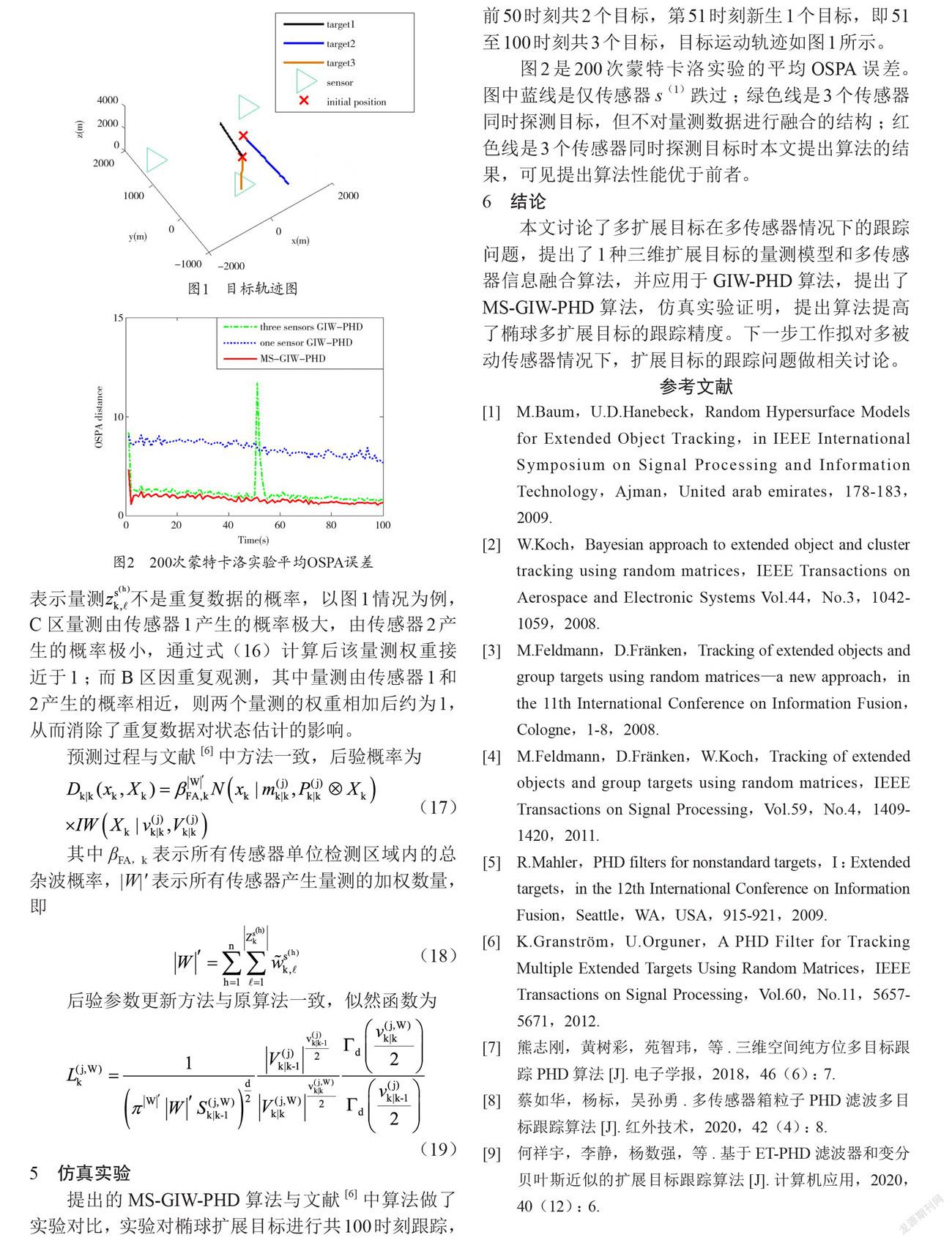
将式(15)带入式(16)可求解。这里,表示量测不是重复数据的概率,以图1情况为例,C区量测由传感器1产生的概率极大,由传感器2产生的概率极小,通过式(16)计算后该量测权重接近于1;而B区因重复观测,其中量测由传感器1和2产生的概率相近,则两个量测的权重相加后约为1,从而消除了重复数据对状态估计的影响。
预测过程与文献[6]中方法一致,后验概率为
(17)
其中βFA,k表示所有传感器单位检测区域内的总杂波概率,|W|'表示所有传感器产生量测的加权数量,即
(18)
后验参数更新方法与原算法一致,似然函数为
(19)
5 仿真实验
提出的MS-GIW-PHD算法与文献[6]中算法做了实验对比,实验对椭球扩展目标进行共100时刻跟踪,前50时刻共2个目标,第51时刻新生1个目标,即51至100时刻共3个目标,目标运动轨迹如图1所示。
图2是200次蒙特卡洛实验的平均OSPA误差。图中蓝线是仅传感器s(1)跌过;綠色线是3个传感器同时探测目标,但不对量测数据进行融合的结构;红色线是3个传感器同时探测目标时本文提出算法的结果,可见提出算法性能优于前者。
6 结论
本文讨论了多扩展目标在多传感器情况下的跟踪问题,提出了1种三维扩展目标的量测模型和多传感器信息融合算法,并应用于GIW-PHD算法,提出了MS-GIW-PHD算法,仿真实验证明,提出算法提高了椭球多扩展目标的跟踪精度。下一步工作拟对多被动传感器情况下,扩展目标的跟踪问题做相关讨论。
参考文献
[1] M.Baum,U.D.Hanebeck,Random Hypersurface Models for Extended Object Tracking,in IEEE International Symposium on Signal Processing and Information Technology,Ajman,United arab emirates,178-183,2009.
[2] W.Koch,Bayesian approach to extended object and cluster tracking using random matrices,IEEE Transactions on Aerospace and Electronic Systems Vol.44,No.3,1042-1059,2008.
[3] M.Feldmann,D.Fränken,Tracking of extended objects and group targets using random matrices—a new approach,in the 11th International Conference on Information Fusion,Cologne,1-8,2008.
[4] M.Feldmann,D.Fränken,W.Koch,Tracking of extended objects and group targets using random matrices,IEEE Transactions on Signal Processing,Vol.59,No.4,1409-1420,2011.
[5] R.Mahler,PHD filters for nonstandard targets,I:Extended targets,in the 12th International Conference on Information Fusion,Seattle,WA,USA,915-921,2009.
[6] K.Granström,U.Orguner,A PHD Filter for Tracking Multiple Extended Targets Using Random Matrices,IEEE Transactions on Signal Processing,Vol.60,No.11,5657-5671,2012.
[7] 熊志刚,黄树彩,苑智玮,等.三维空间纯方位多目标跟踪PHD算法[J].电子学报,2018,46(6):7.
[8] 蔡如华,杨标,吴孙勇.多传感器箱粒子PHD滤波多目标跟踪算法[J].红外技术,2020,42(4):8.
[9] 何祥宇,李静,杨数强,等.基于ET-PHD滤波器和变分贝叶斯近似的扩展目标跟踪算法[J].计算机应用,2020,40(12):6.
