两轮平衡机器人系统控制方法探究

王煜

[摘    要]两轮平衡机器人的工作原理类似于倒立摆，控制器在自平衡和稳定中起着至关重要的作用。文章介绍了一种两轮平衡机器人的设计。文章的重点是使用线性二次调节器（LQR）控制器来控制两轮平衡机器人。通过6轴传感器来进行互补滤波得到姿态信息，通过编码器得到机器人的速度信息。两轮平衡机器人的控制采用LQR控制器，其中包含调节电机速度和旋转方向。LQR控制建模基于线性运动方程，其中的运动学和电气参数通过实验确定。实验结果表明，LQR控制器能够很好地将两轮机器人保持在平衡状态。

[关键词]两轮平衡机器人;LQR控制器;互补滤波

[中图分类号]TP242 [文献标志码]A [文章编号]2095–6487（2022）03–00–03

Research on Control Method of Two-Wheel Balancing Robot System

Wang Yu

[Abstract]The working principle of a two-wheeled balancing robot is similar to an inverted pendulum， and the controller plays a crucial role in self-balancing and stability. This paper presents the design of a two-wheeled balancing robot. The focus of the article is the use of a Linear Quadratic Regulator （LQR） controller to control a two-wheeled balancing robot. The attitude information is obtained by complementary filtering through the 6-axis sensor， and the speed information of the robot is obtained through the encoder. The control of the two-wheeled balancing robot adopts the LQR controller， which includes adjusting the motor speed and rotation direction. The LQR control modeling is based on linear equations of motion， where the kinematics and electrical parameters are determined experimentally. The experimental results show that the LQR controller can keep the two-wheeled robot in a balanced state well.

[Keywords]two-wheeled balancing robot; LQR controller; complementary filtering

如今，帮助人类工作的机器人技术发展迅速，出现了多种不同尺寸、形状和运动的机器人。其中，两轮平衡机器人是1个具有高度非线性动力学的开环不稳定系统。两轮平衡问题在控制工程领域十分常见。例如倒立摆，它通常用作工业机器人，类似于安装在底座上的倒置的手臂。

最近，模糊逻辑和神经网络等软计算技术已被用于控制两轮平衡机器人。此外，基于人工神经网络的实时切换动态控制器旨在解决各种松散表面（如沙子、卵石和土壤）的平衡问题。

但许多与平衡机器人课题相关的研究人员仍然专注于平衡控制本身。有研究运用拉格朗日法建立控制力矩陀螺自平衡车静止情况下的系统动力学模型，线性化后得到其状态空间表达式，在此基础上设计LQR控制器，并采用粒子群优化算法确定Q，R权重系数矩阵。

1 两轮平衡机器人系统简介

系统中的控制器由两部分组成，分别是直立控制和速度控制。直立控制部分中，微控制器将陀螺仪和加速度计采集到的车体倾角信息进行卡尔曼滤波。微控制器对机器人当前运动数据滤波后，基于LQR控制器对机器人进行控制。

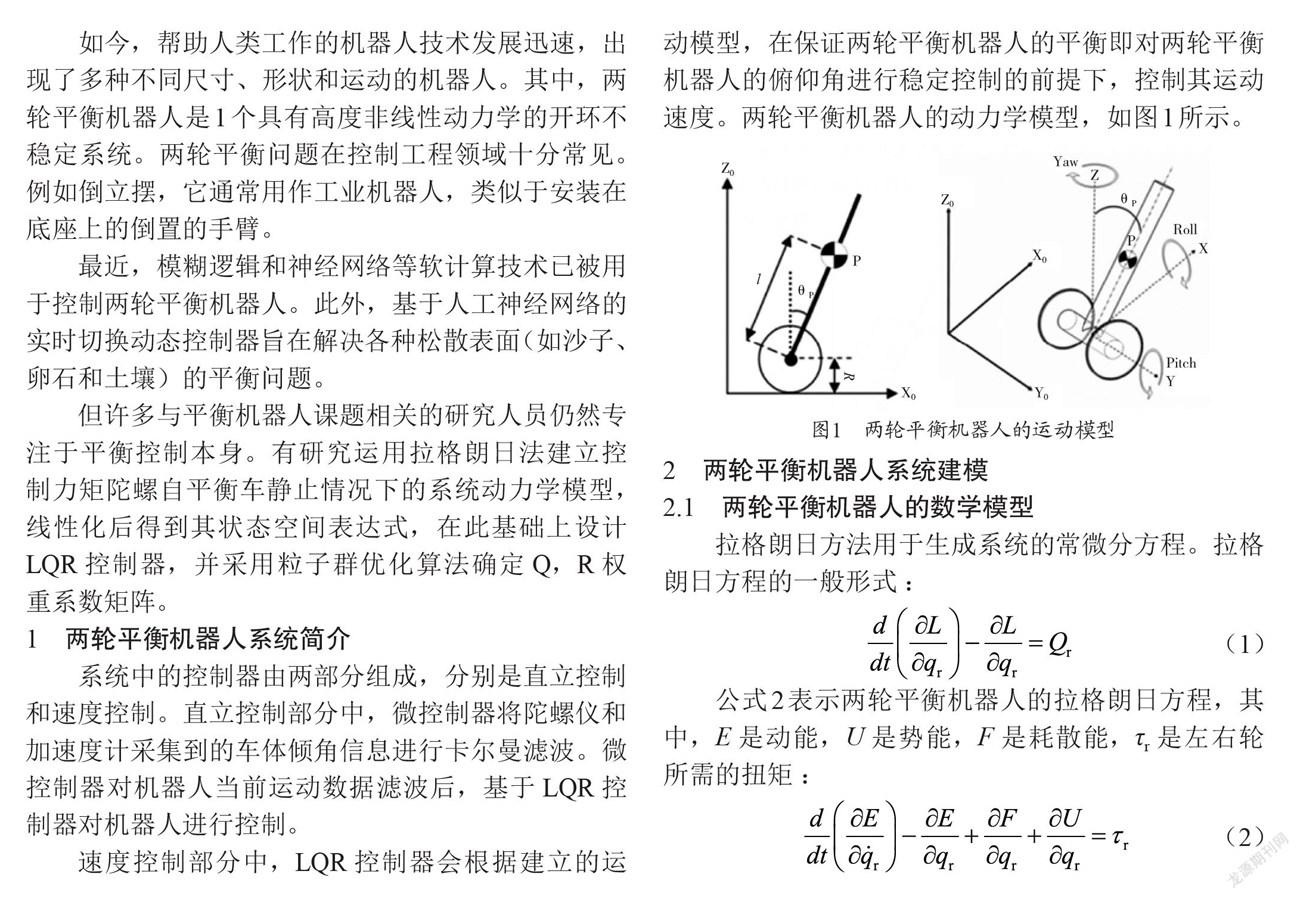
速度控制部分中，LQR控制器會根据建立的运动模型，在保证两轮平衡机器人的平衡即对两轮平衡机器人的俯仰角进行稳定控制的前提下，控制其运动速度。两轮平衡机器人的动力学模型，如图1所示。

2 两轮平衡机器人系统建模

2.1 两轮平衡机器人的数学模型

拉格朗日方法用于生成系统的常微分方程。拉格朗日方程的一般形式：

（1）

公式2表示两轮平衡机器人的拉格朗日方程，其中，E是动能，U是势能，F是耗散能，τr是左右轮所需的扭矩：

（2）

底盘的平移动能（ETKC）和旋转动能（ERKC）组成底盘的总动能（EKC）：

EKC=ETKC+ERKC

（3）

车轮的平移动能（ETKW）和旋转动能（ERKW）组成车轮的总动能（EKW）：

EKW=ETKW+ERKW

（4）

机器人运动的总能量（E）即底盘总动能（EKC）与车轮总动能（EKW）相加：

E=EKC+EKW

（5）

假设机器人移动时高度不会变化。因此，系统的总势能（U）由公式6定义：

U=mglcosθP （6）

系统的总耗散能（F）由公式7定义：

F=μ0v2+μ1ωP2 （7）

选择平衡机器人的位移作为拉格朗日系统方程的第1个一般变量（q1），即q1=x。根据拉格朗日方程的一般形式（公式8）建立系统一阶微分方程：

（8）

选择平衡机器人的俯仰角作为拉格朗日系统方程的第2个一般变量（q2），即q2=θP。根据拉格朗日方程的一般形式（公式2）建立系统一阶微分方程：

（9）

公式8和9是兩轮平衡机器人的两个非线性方程，平衡机器人只有1个平衡点，即机器人平衡或直立时。考虑平衡机器人运动时俯仰角变化较小，假设运动过程中θP≈0。因此，sinθP≈θP，cosθP=1。

将公式8和9非线性方程在平衡点处线性化处理，得到两轮平衡机器人的线性方程。公式10和11表示系统运动的线性方程：

（10）

（11）

2.2 两轮平衡机器人的状态空间方程

公式12和13是动态系统的一般状态空间模型的2个方程。

=AX+Bu （12）

Y=CX+Du （13）

选取4个状态变量用于控制两轮平衡机器人。状态向量的4个元素分别是底盘位移x，底盘俯仰角θP，底盘速度v，底盘角速度wP。

（14）

结合公式10和11，确定系统状态空间方程中的状态矩阵为：

（15）

（16）

其中：

根据机器人相关机械参数以及上述公式，最终得到状态空间方程：

3 LQR控制器

在本文中，LQR控制器用于控制两轮平衡机器人。LQR控制器可用于处理多变量系统，也称为状态反馈控制系统。最优控制将被写为状态反馈，参考公式17：

（U（k）=-Kx（k） （17）

为确定增益矩阵K，代价函数J（公式18）应最小化：

（18）

Q和R是状态的权重函数，分别与控制器精度与控制器输出量有关。优化控制器设计的关键是选择合适的加权矩阵Q和R。目前普遍采用的方法是通过仿真和试验来选择Q和R。

在MATLAB中，可以使用命令lqr（A，B，Q，R）获得增益矩阵为K的线性状态反馈控制器（公式17）。根据上述状态空间方程，可以得到增益K（图2）。

4 实验结果

实验初期电机发出明显的嗡嗡声，结合数据反馈，判断问题在于控制器对状态误差过于敏感，高频驱动直流电机，电机与轮之间连接的结构高频振动。因此重新调节Q和R矩阵，不断地进行优化，最终确定了增益矩阵K=[0.15 2.35 0.1 5.5]。

实验中期望两轮平衡机器人以一定的速度原地转动，从实验数据来看，两轮平衡机器人的俯仰角的抖动很小，调节时间在300 ms左右。地面上细小的不平整处未能对机器人的平衡产生影响。输出的PWM抖动情况较调参前有明显改善。机器人整体运行情况良好，控制效果达到理想目标。

5 结束语

本文描述了两轮平衡机器人LQR控制器的设计过程，成功实现了机器人的平衡运动。LQR最优控制具有易于控制并兼顾多项性能指标效果的优点。两轮平衡机器人系统通过这种控制方式可以稳定、平滑得运动，机器人可以通过两个轮子可以可靠地平衡直立。未来的工作展望，我们可以进一步考虑如何对平衡机器人的航向角进行建模与控制，并且基于这一完整的运动控制，通过摄像头与激光测距传感器来完成一定程度上的室内导航与避障。

参考文献

[1] 单钧麟，汪立新，秦伟伟，等.控制力矩陀螺自平衡车粒子群优化LQR控制[J].四川兵工学报，2019，40（12）：100-104.

[2] 冯健.基于LQR算法的列车自动驾驶系统最优控制研

究[D].西南交通大学，2014.