电商仓储订单分批和路径优化问题的分支定价算法研究
2022-05-10陈彦博文若霖
陈彦博,陈 峰,文若霖
(上海交通大学 中美物流研究院,上海 200030)
随着电商平台的快速发展与普及,电商交易量及物流量快速增长。2020年,中国快递业务量和收入分别完成630亿件和7 450亿元,同比增长24%和23%。物流对于电子商务的作用越来越大,以平台销售为主的电子商务逐渐转变成以仓储运作与服务为主的现代化电商模式。因此,仓储物流成为了电商服务质量的一个重要问题和瓶颈之一。实际的电商仓储拣选作业流程如图1所示。电商仓储库区中,通常采用人工拣选的方式,货架为统一的低位货架,库区中会按照货位进行编号,以便拣选人员进行拣货。
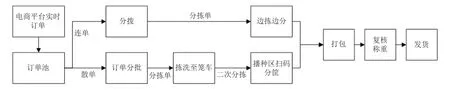
图1 电商仓储拣选作业流程Figure 1 E-commerce warehouse picking process
在拣选作业中,常遇到以下问题:1) 大量相似度高的商品未能有效合并,造成多次重复拣选;2) 实际拣选作业中大规模订单未能合理安排,拣选人员众多但实际效率不高。为了解决订单拣选的问题,本文研究电商仓储的订单分批和路径优化问题,本质上是订单分批问题和路径优化问题的组合优化问题。针对这两个问题,近年来许多学者都对这方面进行过许多研究。
订单分批问题,可以看作特殊的装箱问题。装箱问题的目标是希望能用尽量少的容器装入更多的物品,同装箱问题稍有所不同,订单分批的目标是批次的总拣选路径距离最短,且包含所有的订单。Hwang等[1]用聚类的方法,将订单的相似度定义为向量的相似度,通过计算向量相似度,将订单进行合并。陈方宇[2]定义了基于偏离度的相似性,并在多区块的库区中,通过偏离度相似性对订单分批进行求解。
订单路径优化问题中,对每一位拣选员来说,可以看作是特殊的旅行商问题,其目标是使每个批次内单一拣选员完成批次所有订单商品的拣选任务所需要行走的距离最小。解决拣选中的路径优化问题,通常有两种方向,一种是基于启发式的行走策略,另一种是基于网络的策略。Öncan等[3]对路径优化问题进行建模,建立混合整数规划模型,并分别利用S型策略、返回策略及中点策略对问题进行求解。李诗珍等[4]在S型策略的基础上,提出一种动态规划的算法对问题进行求解,保证在既定规则下的最优拣货路径。
随着订单分批和路径优化问题研究的不断深入,相关学者开始对订单分批和路径优化的组合优化问题进行研究。Won等[5]较早开始对订单分批和路径优化问题进行研究,将批次的整体处理时间作为优化目标,并构建一个整数规划模型进行求解。Kulak等[6]提出基于聚类的禁忌搜索算法用于求解订单分批和路径优化问题。Valle等[7]针对联合订单分批和路径优化问题提出一个混合整数规划模型,并通过分支定界割平面的方法进行求解。Valle等[8]在此基础上,又提出一个近似模型,将路径优化中的TSP (travelling salesman problem,旅行商问题) 问题转化为一个近似模型进行求解。Hong等[9]考虑拣选过程中可能产生的堵塞问题,并提出启发式算法进行求解。Van Gils等[10]提出一个考虑拣选时间的混合整数规划模型,并通过局部搜索对模型进行求解。Briant等[11]考虑一个HappyChic的特定仓储拣选模式下的订单分批问题,并通过列生成算法对问题进行了分解并求解。也有很多学者从工作负荷[12]、交付时间[13]、工作时间[14]等方面对问题进行研究。
精确算法之外,元启发式算法也广泛应用于订单分批和路径规划问题中。Chen等[15]提出蚁群算法用于多区块、多通道的订单拣选问题中。之后,在蚁群算法的基础上实现了许多元启发式的组合算法。Li等[16]结合蚁群算法和邻域搜索。De Santis等[17]结合Floyd算法和蚁群算法。Chen等[18]结合蚁群算法和遗传算法。启发式算法可以较快地获得一个近似解,并且经过不断的研究和扩展,也已比较成熟。
现有研究中已经包含对于订单分批和路径优化问题的混合整数规划建模和求解。但主要基于启发式算法,并且没有对大规模问题进行较为深入的研究。本文在上述研究的基础上,考虑在电商仓储环境下的库区中,如何合理地对订单进行分批,并使得每一个批次中的路径最优。在此基础上建立混合整数规划模型,针对提出的模型设计分支定价算法,构造模型的主问题和子问题;通过列生成算法获得限制主问题的近似最优解;再利用分支定界法对初始解进行改进,获得最优整数解;最后使用算法进行数值实验,通过多组数值实验和案例验证模型的有效性和算法的高效性。
1 问题描述和数学模型
1.1 问题描述
本文研究面向电商仓储的订单分批和路径优化问题,其对象是具有多区块、多通道、多交叉点物理布局的仓库,如图2所示。拣货路径从起点出发,沿虚线经过货架间的通道和通道间的交叉点,拣选所有货物后,再回到起点。问题具体描述如下。

图2 拣货路径图Figure 2 Picking routing
假设库区为一个有向图G=(V,A),其中,V为库区网络中所有顶点集合,包括起点和多个货位点,共有vmax个 顶点;A为网络中各个货位点所连接的弧的集合,其中弧 (i,j)∈A,弧之间的距离为di j。O代表所有需要拣选的订单集合,数量为n;订单分批的批次集合为B,包含的批次数量为m。从订单分批到完成拣选,需要解决分批和路径优化两个问题,其中的路径优化实际上是一个TSP问题。对于每一个批次b中 的所有订单O′,以xij作 为弧 (i,j)的决策变量,要使得批次内的所有货物拣选的路径xijdij最优。优化每一个批次的路径后,同时需要优化每个批次中的订单集合O′,在满足每个批次不超过订单容量上限C的情况下,使得总距离最短。因此,本文研究的是同时考虑订单分批和路径优化的组合优化问题。在这个问题中,不考虑拣选员的工作负荷,假设每个拣选员拥有相同的行走速度和拣选熟练度,优化只考虑行走的距离最优。
1.2 集合及变量
为解决如上问题描述,综合考虑订单分批问题和路径优化问题,建立一个混合整数规划模型,目标是使得所有订单进行分批后总拣选距离最优。同时考虑有向图中可能存在货位点和只用于行走的交叉点。首先,给出以下建立模型所需的集合、参数变量和决策变量。
集合:
O={1,2,···,n},为包含所有订单的集合;
B={1,2,···,m},为包含所有批次的集合;
V={0,1,2,···,vmax},为包含所有顶点的集合;
参数变量:
C为每个批次的订单数量上限;
di j为顶点i到j的距离;
Aij为弧 (i,j)是否在网络图中,是则为1,否则为0;
li为顶点i是否为一个货位点,是则为1,否则为0;
Uoi为 订单o中 是否包含货位点在i的货物,是则为1,否则为0。
决策变量:
为 批次b中 的路径是否经过弧 (i,j),是则为1,否则为0;
为批次b中 是否包含订单o,是则为1,否则为0;Qb为批次b是否至少包含一个订单(被选择),是则为1,否则为0;
为批次b中 顶点i的出度。
国外的餐饮企业充分的调动了社会资源,实行轻资产运营,在供应链和中央厨房的选择上,并不自己建设,而是采用参股或者合作的方式,组织非常灵活,没有任何重资产,例如麦当劳、肯德基。
1.3 模型建立
建立如下混合整数规划(MIP)模型。


其中,目标函数(1)表示最小化所有批次的总拣选行走距离,约束主要可以分为2个部分。
约束(2)~(6)表示对于批次中的路径优化。约束(2)保证批次中每一个弧 (i,j)的流量平衡,如果从弧中的一个点进入,则必然会从该点去往另一个点。约束(3)、(4)保证在一个批次中,如果至少包含一个订单,那么它的路径必须包含起点 0。约束(5)、(6)用于消除路径优化中的子回路,其中约束(5)表示在批次中某一个顶点的出度;约束(6)则是利用出度的性质,消除可能产生的子回路。
约束(7)~ (14)表示对于所有订单分批。约束(7)保证订单的数量不超过批次的订单容量约束。约束(8)保证每一个订单只包含在唯一的批次内。约束(9)表示批次节点与订单的关系,如果有一个订单被安排到一个批次中,那么这个订单中包含商品的库位顶点至少将被访问一次。约束(10)表示批次、订单、弧之间的关系,当订单在一个批次中,该批次才能够包含可被访问的弧。约束(11)表示只有当批次中含有订单才选择批次。约束(12)~ (14)定义了变量的类型。
2 分支定价算法设计
为解决大规模问题、加快求解速度,本文针对提出的订单分批与路径优化问题设计分支定价算法,利用列生成算法对大规模问题进行分解。将混合整数规划模型松弛为线性规划模型,并将问题分解为主问题和子问题(价格问题)。主问题对选定的分批形式进行选择,子问题对每种批次内的货物拣选路径进行求解。每求一次子问题,便将对应的检验数为负的“列”(批次)加入到主问题中,相当于修正的单纯形法。将新列作为进基变量加入主问题,再对主问题求解,迭代直至所有检验数非负,找到主问题的最优解。若主问题的最优解为整数,即得到订单分批和路径优化问题的最优解;否则,利用分支定界算法,获得原问题的最优整数解。
2.1 主问题模型 (master problem,MP)
首先要将模型转换为集合覆盖模型,才能满足列生成算法的要求。假设S表示满足批次容量的O中所有订单的所有可能批次订单组合子集:S={s1,s2,···,。其中,s∈S表示列生成中所需要的“列”。订单与列之间的关系,通过决策变量来表示:,其中n表示表示订单的数量。每个表 示这个“列”s的批次订单组合中是否包含订单o中的所有货物。由于集合覆盖模型中不再有顶点的含义,因此用ds表 示拣选所有s中订单的货物的最优路径距离。因此,实际上S表示了所有满足批次订单容量限制的可行路径的集合,而其中的每一个s,不止可以当作一个批次订单组合,也可以表示一条可行的路径,而ds就 表示最优路径s的距离。因此,主问题模型就转换为一个选择路径的集合覆盖模型。
令变量 αs∈{0,1}表 示是否选择了路径s。可以得到一个整数规划模型作为主问题如下。

其中,目标函数(15)表示所有选择的路径(批次订单组合)的总距离最小;约束(16)确保每个订单都被拣选。为了使用列生成算法,需要将这个问题进行线性松弛,得到一个新的线性主问题(linear master problem,LMP)。此外,由于集合S的数量随订单的数量以指数增加,因此需要对主问题进行松弛。令S′表 示S的一个子集,定义该问题的一个限制主问题(restricted linear master problem,RLMP)如下。
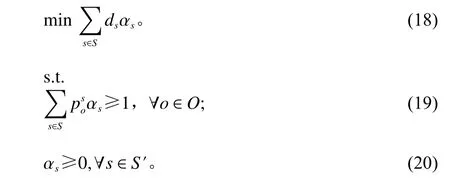
2.2 子问题模型 (sub-problem,SP)
由rs的定义,对应的子问题如下。
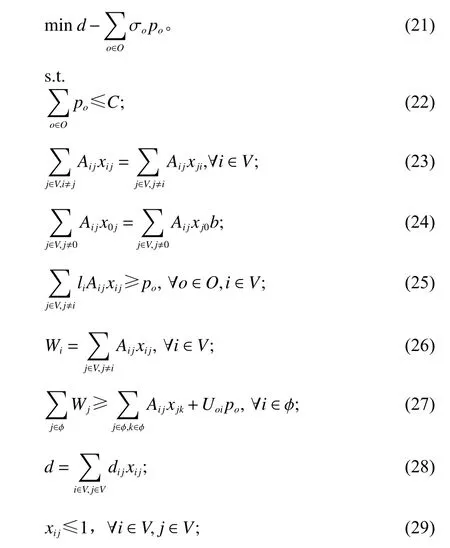

其中,po表 示是否选择了订单o。约束(22)表示每个批次中的最大容量不超过C。约束(23)保证网络中的流量平衡。约束(24)保证每条路径从起点出发。约束(25)表示xij与po之 间的关系:如果选择了订单o,则必须经过订单o中的某一个货位点。约束(26)、(27)用于消除可能产生的子回路。约束(28)表示子问题中距离d的计算方式,通过求解子问题的线性松弛问题,能够得到xij的 整数解,进而获得po的解。
2.3 生成初始可行解
在列生成算法中,主问题首先需要通过初始可行解,得到一个对偶值,代入子问题中进行求解获得检验数。因此,在算法开始时需要生成一个初始解。初始解包含多个“列”,即多种批次的可能订单情况。由于可行解必然包含所有的订单,因此为了快速生成一个初始可行解,则可以按订单次序,生成批次数量最小的订单批次组合。例如:当前有100个订单,假设每个拣选员分配到的批次订单上限为8个订单,则按订单次序,将100个订单填满12个批次,最后4个订单放到第13个批次中。这样即可生成一个最简单的初始可行解(列)。而对于每一个初始可行解,还要求解其最优路径,因此对于初始可行解的每一个批次,都利用TSP模型对其求解一个最优的距离ds,求解模型如下。

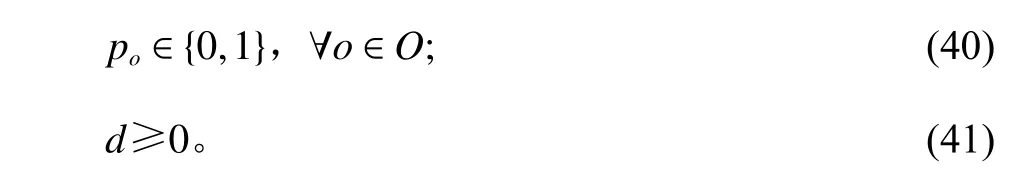
其中,变量及参数与子问题相同,约束中去除子问题中主问题解的对偶值的影响。
2.4 算法具体步骤
根据上文的主问题、子问题模型,实现对于原问题的分解,原问题被分解为一个选择订单批次组合的主问题和单个批次订单组合的TSP子问题。在此基础上,可以实现列生成算法,在生成初始解后,利用列生成算法不断迭代,直至找到限制主问题的最优解。由于原问题希望得到最优的整数解,因此,需要在列生成算法的基础上,通过分支定界法生成新的分支节点进行进一步搜索,将分支节点加入限制主问题中继续求解。若解为整数,则更新上界,直至找不到一个更好的整数解,则此时的上界即为原问题的最优整数解,这也是分支定价算法的过程,如图3所示。因此,分支定价算法的流程可以描述如下。
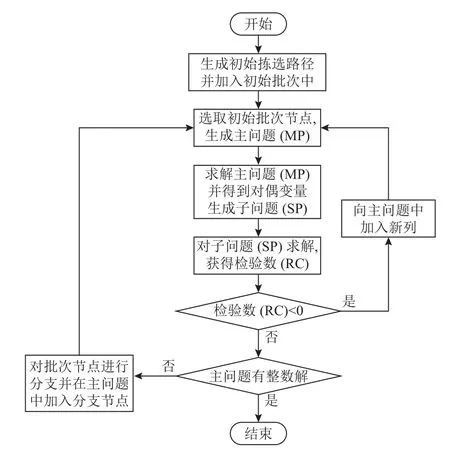
图3 分支定价算法流程图Figure 3 Branch and price algorithm flow
步骤1产生初始解后,加入到主问题的集合S,组成根节点,并作为初始的上界,下界初始为0;
步骤2初始搜索,根据主问题,选择一个节点作为初始解生成初始可行的限制主问题R LMP(S′);
步骤3求解当前限制主问题,获得初始解 αs和对偶变量 σo;
步骤4求解对应的子问题,对于所有的s∈S′,如果检验数均为非负,那么转向步骤6,否则转向步骤5;
步骤5将检验数为负且最小的列s对应的列添加到限制主问题中,转向步骤2;
步骤6如果此时限制主问题的解 αs为整数,转步骤7,否则转步骤8;
步骤7将解的目标值与当前的上界进行比较,如果小于上界,则更新上界值;
步骤8删除当前节点,根据分支定价的策略进行分支,更新批次路径集合S,生成分支节点,加入搜索树中;
步骤9若搜索树非空,则转向步骤3,否则转向步骤10;
步骤10当前的上界即为最优解。
3 数值实验
3.1 模型与算法的验证分析
为了验证模型的准确性,本文利用IBM ILOG CPLEX 12.10对原模型进行求解,然后与分支定价算法的求解结果进行比较。实验设计了3组仓储示例,货位点数量分别为6、12、32。每组实例中,分别设置3组订单数量,批次数量不同的算例进行测试,实验参数如表1所示。表2是小规模的实验结果,其中d表示总最优路径(m),t表示求解时间(s)。从结果可以看出,直接利用CPLEX求解和使用分支定价法求解可以得到相同的整数解,随着规模的逐渐增加,分支定价法求解的速度将会明显优于CPLEX,并能够得到一个同样精确的结果。

表1 小规模实验参数Table 1 Parameters of small scale experiment

表2 小规模实验求解结果Table 2Results of small scale experiments
3.2 大规模的实验分析
由于在大规模问题中,直接利用CPLEX求解器求解需要非常长的时间,因此,对于大规模问题,通过分支定价算法对其求解,能提高求解速度,并且也能够获得精确解。为了验证分支定价算法对于大规模问题的可行性,本文设计了12组算例进行实验。仓储货位分布如图2所示,有72个货位点和12个交叉点,货架节点间的距离设置为1,实验参数如表3所示。结果如表4所示。通过结果可以看出,分支定价算法针对规模较大的订单分批和路径优化问题,也可以在一个可接受时间内获得精确解,因此也验证了分支定价算法对于大规模订单分批和路径优化问题的可行性。
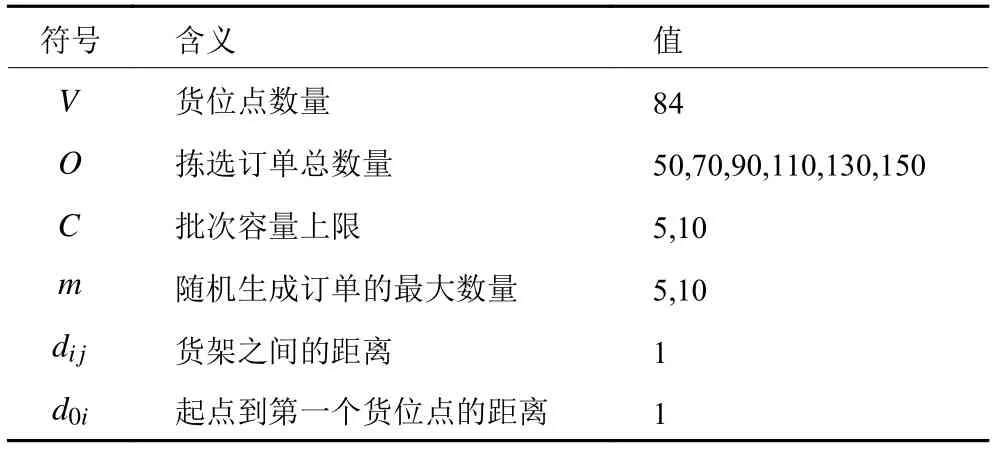
表3 大规模实验参数Table 3 Parameters of large scale experiments
结合表4的数值实验结果,同时分析订单数量和单个订单内货物数量大小对于求解速度的影响,如图4、图5所示。求解时间会随着订单规模的增大发生比较明显的上升,但总体而言,在处理大规模问题时,分支定价算法依然可以在有限时间内得到一个精确解,满足实际的求解需要。
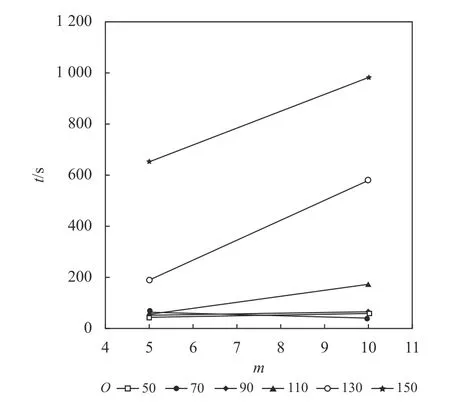
图4 不同订单规模求解时间Figure 4 Solution time of different order size

图5 不同订单规模求解时间增长趋势Figure 5 Time growth trend of different order sizes

表4 大规模实验结果Table 4Results of large scale experiments
4 案例分析
本文以实际的电商第三方仓储企业的库区作为实例进行分析。图6是某个单一库区的布局图。库区中共有26个货位点、12个交叉点,所有的货架采用标准的低位货架,忽略拣选过程中不同货架的拣选难度和不同拣选员的熟练度。在实际的仓储环境中,与数值实验中模拟数据不同的主要有两点。获取的订单数量不是一个固定的值,在不同的时间订单的数量差异很大,而由于拣选对时间的要求较高,因此需要固定一段时间就进行一次订单分批。在实际的货位中,每种商品可能对应的货位不止一个,即在同一个库区中,某种商品可能存在2个以上的货位点。
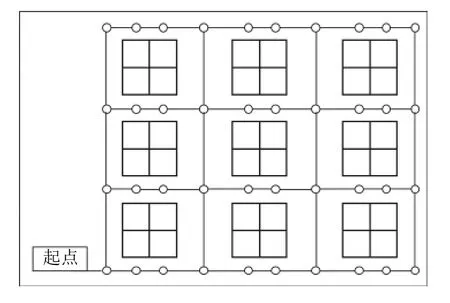
图6 某第三方电商仓储区域Figure 6 Storage area of a third-party e-commerce warehouse
针对以上的不同,在实际的分批计算前,需要作一定的处理。订单的数量由每20 min到达的订单数作为一次需要处理的订单数据。而对于订单与货位点关系的问题,在数据处理中,需要对变量Uoi进行调整,由原来的订单与货物的关系,转变为订单与货位点的关系,是则为1,否则为0。
在此基础上,考虑实际的仓储库区环境进行建模求解,累计对2 h的实时订单进行分批,每个分批的容量上限为20。不同时间的订单数量用O表示,每段时间的平均订单商品数用pmean表示,每段时间的订单最大商品数用pmax表示。得到表5中的结果。总体来看,平时段(20 min)的平均订单数为93.75,每个订单的平均商品数为4.66,通过分支定价算法求解,平均的求解时间为138.11 s,可以满足实际的仓储作业需要,证明了本文的模型和算法可以在实际中应用。

表5 实际案例的求解结果Table 5Results of practical cases
5 结论
本文对电商仓储的订单分批和路径优化问题进行描述,结合现有研究,提出电商仓储环境下的订单分批和路径优化问题的混合整数规划模型。由于电商环境下的订单规模巨大,为求解大规模问题,本文设计分支定价算法进行求解,将初始模型松弛为线性规划模型,并利用列生成算法对问题进行分解,分别求解主问题和子问题,循环迭代找到松弛问题的最优解,再利用分支定界算法,找到原问题的最优整数解,完成分支定价算法的求解。为了验证模型及算法,设计多组数值实验,在小规模实验中验证了模型的可行性,并设计大规模数值实验,验证了分支定价算法可以较好地求解大规模的订单分批和路径优化算法,并能够得到精确的整数解。最后,利用某第三方电商仓储企业的实际数据进行案例分析,并使用实际数据进行实验,验证本文的模型及算法可以应用于实际的仓储拣选作业中。
6 致谢
感谢上海发网供应链管理有限公司提供的业务与数据支持。
