城市高架轨道交通引发的箱梁振动特性分析

房 建，韦智敏，郑稳稳，雷晓燕，练松良，刘林芽

(1.华东交通大学 轨道交通基础设施性能监测与保障国家重点实验室,江西 南昌 330013；2.华东交通大学 铁路环境振动与噪声教育部工程研究中心，江西 南昌 330013；3.同济大学 道路与交通工程教育部重点实验室，上海 201804)

相对于轮轨噪声，桥梁结构辐射的噪声为低频噪声，具有衰减慢、传播距离远、穿透能力强等特点[1]。箱梁是城市高架轨道交通主要采用的梁型，箱梁辐射的噪声也随之成为研究热点之一。由箱梁辐射噪声产生的机制可知振动是箱梁辐射噪声的根源，箱梁振动特性及分布规律对城市高架轨道总噪声水平具有重要影响，已有研究表明[2]，高架桥梁辐射噪声在20～200 Hz范围内与振动的相干系数很高，说明该频段范围内的辐射噪声几乎均是由桥梁结构振动产生的。因此，研究城市高架轨道交通箱梁20～200 Hz的振动特性对于箱梁结构减振降噪是十分必要的。

针对高架轨道交通箱梁振动与噪声的研究主要有理论计算法和试验法[1,3]。理论计算法通过建立理论模型，利用积分变换法、有限元法、边界元法以及统计能量法对高架轨道结构的振动及噪声进行研究。文献[4]利用积分变换法建立振动能量从钢轨至桥梁的变换模型，然后基于SEA法计算了箱梁辐射的结构噪声。文献[5]采用混合有限元-统计能量分析方法研究预测了钢-混凝土组合连续板梁桥的车致噪声。罗文俊等[6]结合有限元与统计能量法，分析交通荷载引起箱梁结构在不同频段内振动的噪声特性。结果表明，采用FE-SEA混合法预测箱形梁结构噪声可保证精度，提高计算效率，并扩展结构噪声研究的频率范围，提高预测精度。刘林芽等[7]以轨道交通30 m简支槽形梁为研究对象，基于车桥耦合分析模型，利用声传递向量法、有限元法分析了槽形梁辐射的结构噪声特性。试验方法的特点是真实、可靠，但耗资巨大。文献[8-9]以京沪高速铁路32 m混凝土简支箱梁为研究对象，制作1∶10的缩尺模型，通过自由模态测试验证了缩尺箱梁有限元模型的正确性，并通过箱梁有限元模型对比验证了缩尺模型的有效性。韦红亮[10]、战家旺等[11]、房建等[12]分别采用现场实测的方法对铁路高架轨道结构振动与噪声特性问题进行了研究。以上研究得到了很多成果和大量有意义的结论。但针对轨面不平顺引起城市高架箱梁振动特性及分布规律的研究比较缺乏。鉴于此，本文利用有限元和现场实测方式，对轨面不平顺引起城市高架箱梁结构振动特性进行研究，重点分析对桥梁结构辐射噪声具有重要影响的20～200 Hz箱梁振动特性和分布规律，旨在为城市高架轨道结构减振降噪研究提供参考。

1 现场试验

1.1 测点布置和仪器

测点设置于上海市轨道交通3号线，测试传感器为CA-YD-109A压电式加速度拾振器，列车速度为54 km/h，箱梁采样频率为1 000 Hz[12]。桥梁结构为简支梁，横断面如图1所示，跨度为30 m。轨道为支承块式结构，钢轨类型为CHN60，扣件类型为弹条Ⅱ型。为了拾取列车经过时箱梁的垂向加速度信号，在下行线路梁跨中断面的箱梁顶板中心、轨道中心、翼板中心、腹板中心和底板中心5个测点分别布设传感器,如图2所示。

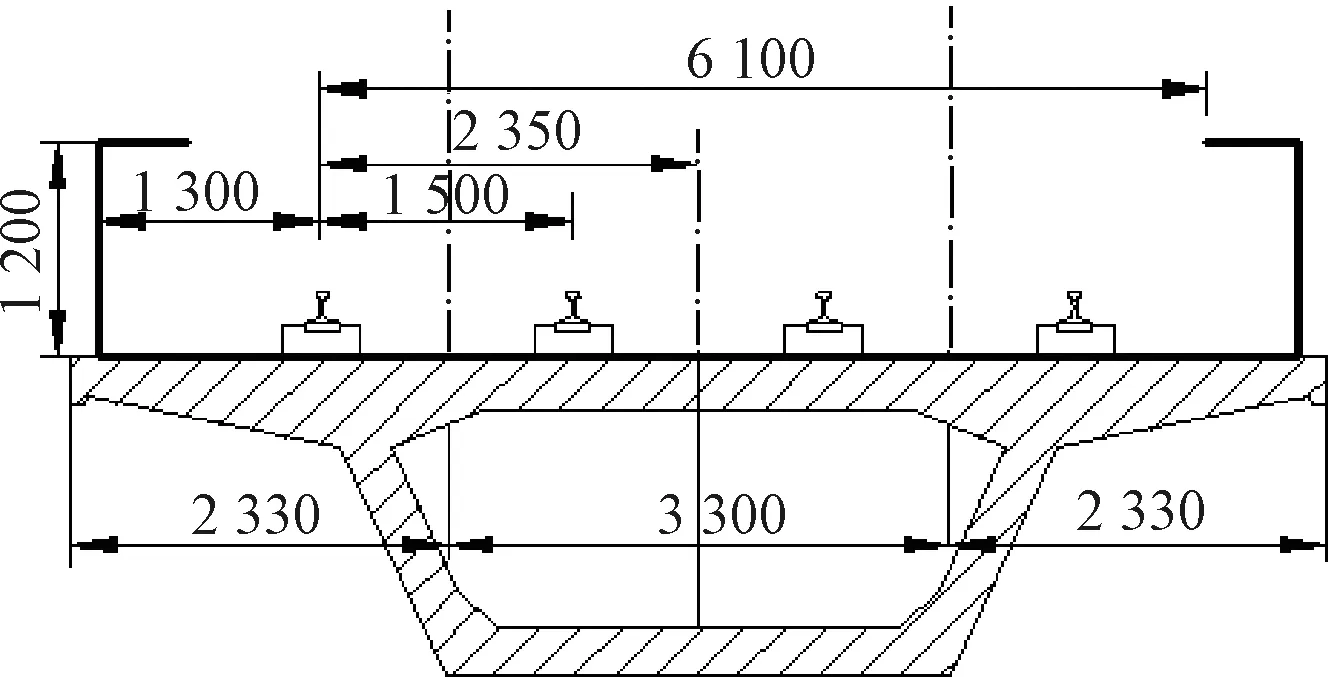
图1 高架箱梁横断面尺寸(单位：cm)

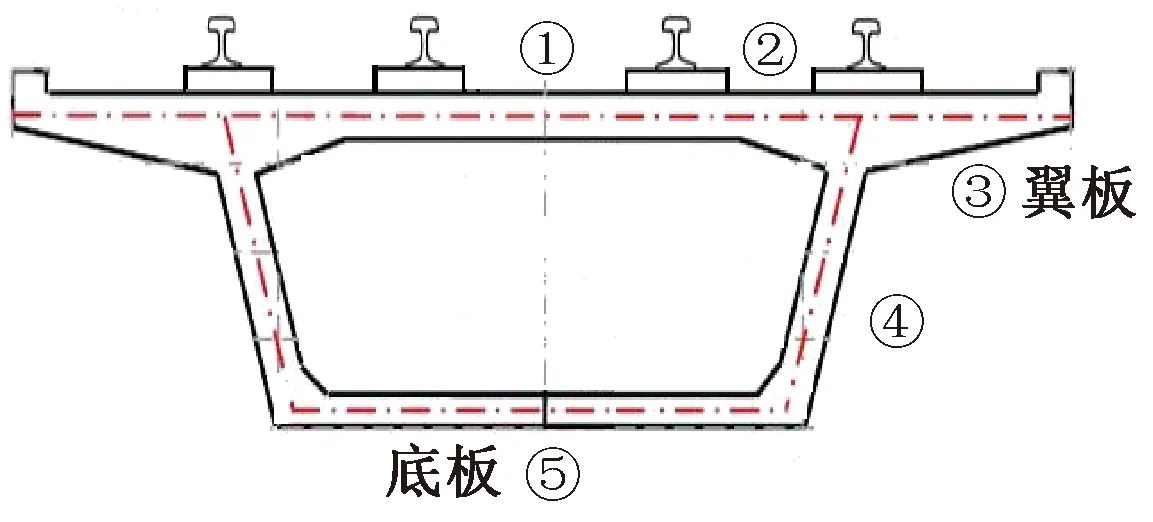
图2 高架箱梁振动测点布置

1.2 数据分析

共采集20组数据，选择第8组数据，得到各测点加速度时程信号，如图3所示，各测点加速度信号的时域统计分析如表1所示。

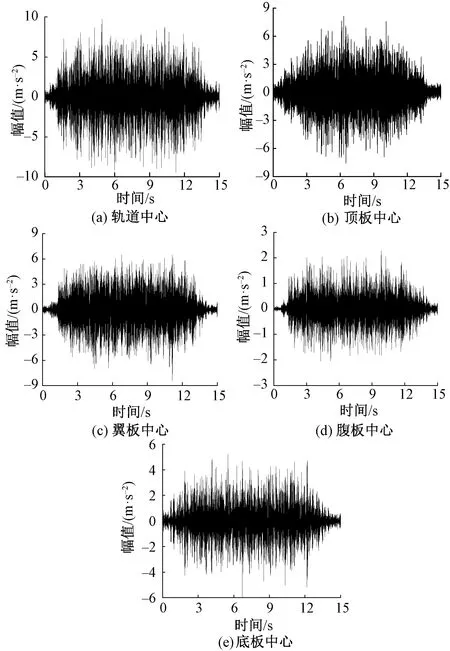
图3 振动信号加速度时程曲线

从表1可以看出，受箱梁结构和轨道结构布置的影响，列车经过时，箱梁顶板轨道中心线的垂向振动响应最强烈，翼板中心和顶板中心的垂向振动响应大致相当，底板中心、腹板中心的垂向振动响应依次减小。

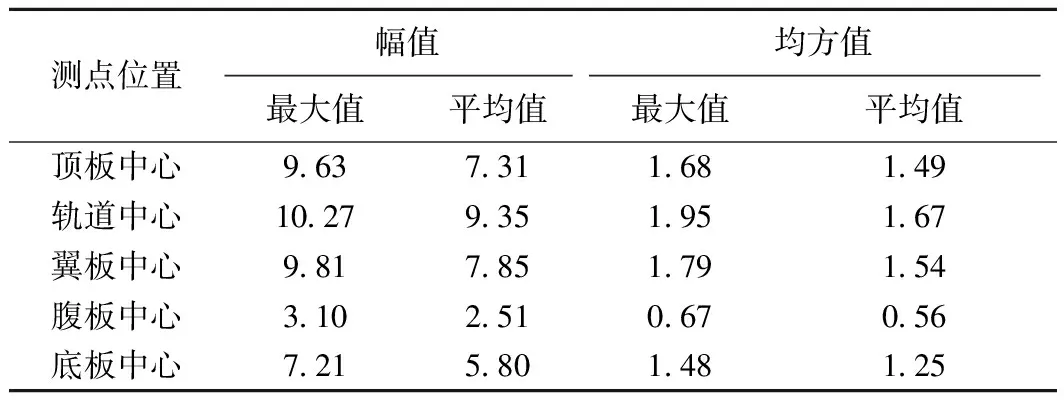
表1 时域统计表 m/s2

为进一步分析箱梁结构振动的频域分布特性，对各测点各组加速度信号进行1/3倍频程分析，然后求取其平均值，得到各测点的1/3倍频程频谱曲线，如图4所示。

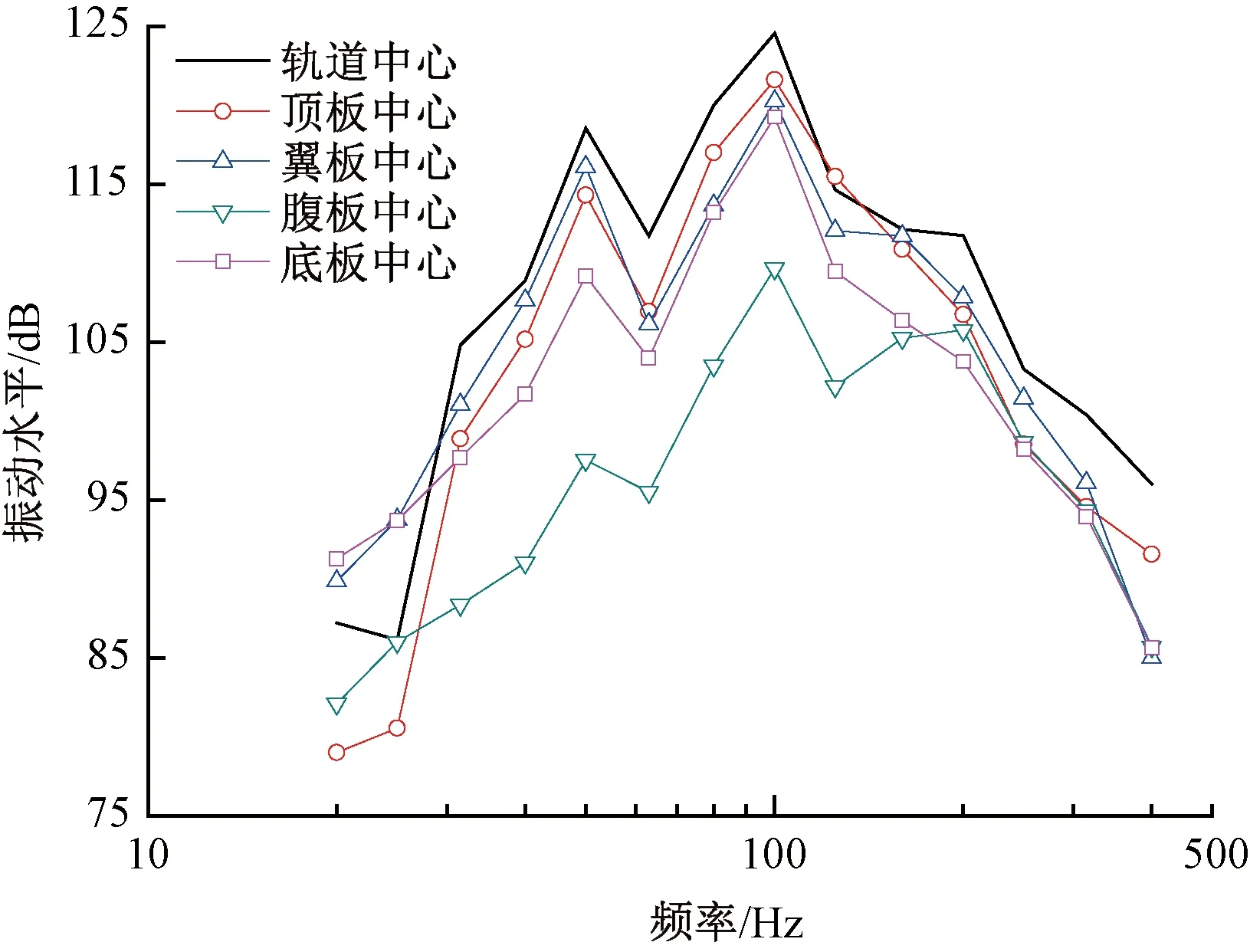
图4 箱梁结构振动频谱图

图4表明，箱梁结构振动主要集中于40～200 Hz范围内，轨道中心、顶板中心、翼板中心和底板中心的垂向振动水平在100～125 dB范围内，腹板中心垂向振动水平也在85～110 dB之间，轨道中心、顶板中心、翼板中心、底板中心和腹板中心垂向振动最大水平分别为125、121、120、119、110 dB。与时域分析一致，在40～200 Hz范围，箱梁顶板轨道中心处垂向振动水平最高，翼板中心和顶板中心振动水平大致相当，底板中心、腹板中心振动水平依次减小。

此外，利用频率、车速、不平顺波长三者的关系式f=v/λ，可以判定振动频率分布在40～200 Hz范围时，波长范围为0.075～0.375 m的轮轨短波不平顺对箱梁振动起主要作用。

2 计算模型

2.1 有限元振动计算理论

基于有限元法对桥梁结构的振动进行分析，可得到在移动荷载作用下结构随时间变化的各节点位移、速度和加速度的响应，其基本方程为

Meüe+Ceue+Keue=Fe

( 1 )

2.2 计算模型及参数

桥梁为30 m净跨单箱单室混凝土简支箱梁，有限元模型如图5所示。

图5 有限元模型

对于轨道结构，采用三维2节点梁单元模拟CHN60型钢轨、三维弹簧阻尼单元模拟弹条Ⅱ型扣件、三维8节点实体单元模拟支承块，对应各网格的最大尺寸分别为0.5、0.05、0.08 m；箱梁结构采用三维4节点壳单元进行模拟，网格最大尺寸为0.2 m。计算模型参数如表2所示，箱梁截面尺寸如表3所示。

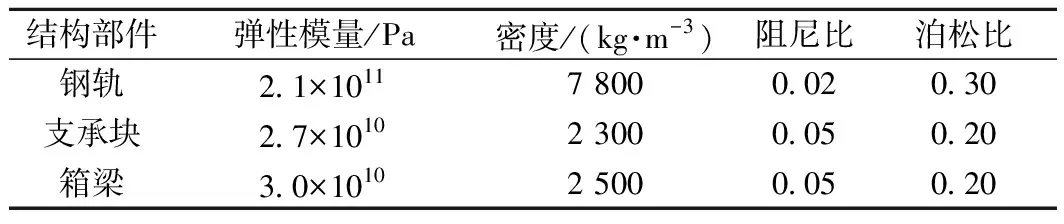
表2 有限元模型参数

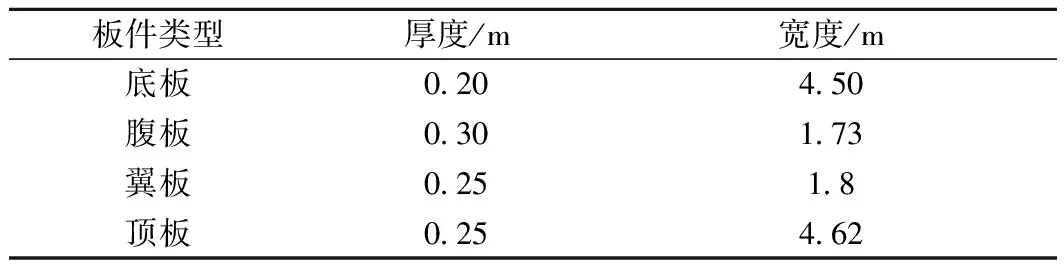
表3 高架桥截面板件等效尺寸

荷载方面，通过SIMPACK软件建立车辆-轨道耦合模型得到轮轨垂向力，将此作为计算模型的激励荷载，车辆为A型车单节编组，轨道不平顺采用文献[10]所述的城市轨道交通直线区段非接头区0.01～1 m波长范围内的轨面短波不平顺统计谱，见图6。车速为60 km/h，不平顺功率谱表达式为

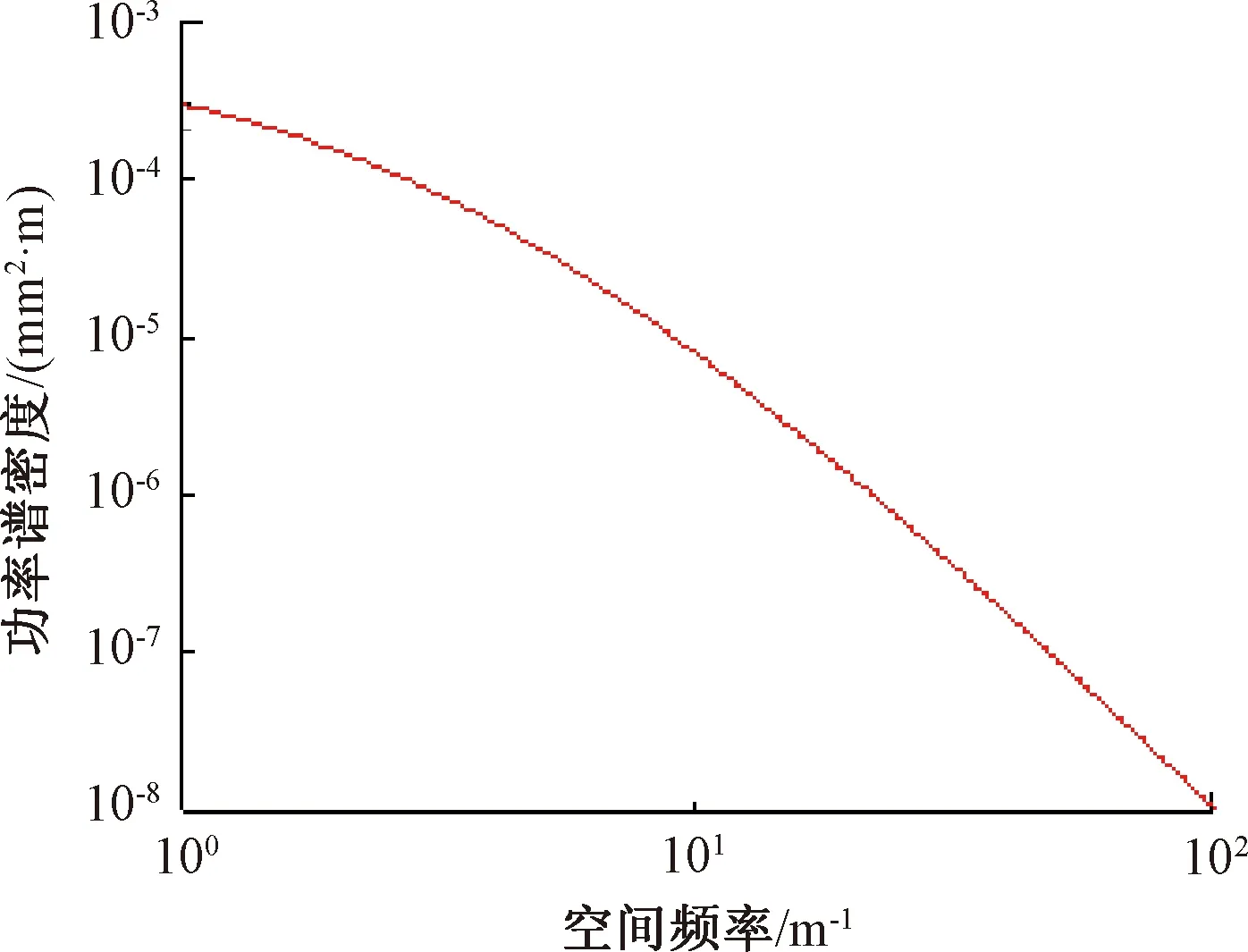
图6 轨面短波不平顺谱

( 2 )

式中：S为功率谱密度，mm2·m；Ω为空间频率，m-1；A1、A2、A3为待定系数，分别取0.035、3.32、3.22。

将计算得到的轮轨垂向力输入有限元模型中进行分析，阻尼分别为α=0.2，β=0.000 2，计算步长为10-3s。为了验证计算模型的有效性，选取顶板中心和腹板中心处理论计算结果与实测值对比分析，结果如图7所示。

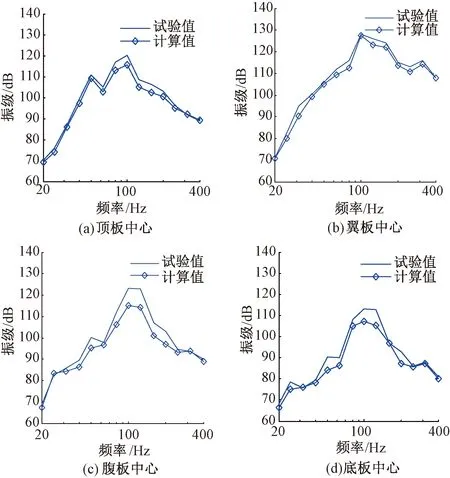
图7 计算模型的验证

图7表明，在31.5～200 Hz频域范围内，计算值与实测值的平均差值为3～5 dB，分析其原因，首先是计算模型的激励荷载与现场实际情况不完全一致；其次，轮轨间的横向作用力使箱梁产生纵向扭转，从而影响箱梁的垂向振动，这也可能导致计算值与试验结果出现偏差。但在20～400 Hz分析频域范围内，理论模型的计算结果与试验结果基本保持了一致性，二者的最大偏差为8.6 dB，这表明计算模型能够满足一定的精度要求。

3 箱梁结构振动特性分析

3.1 自振分析

为了解箱梁的自振特性，分别对15、24、30、36 m净跨的箱梁进行模态分析，提取前200阶的振动频率、累积质量分数，如图8所示。

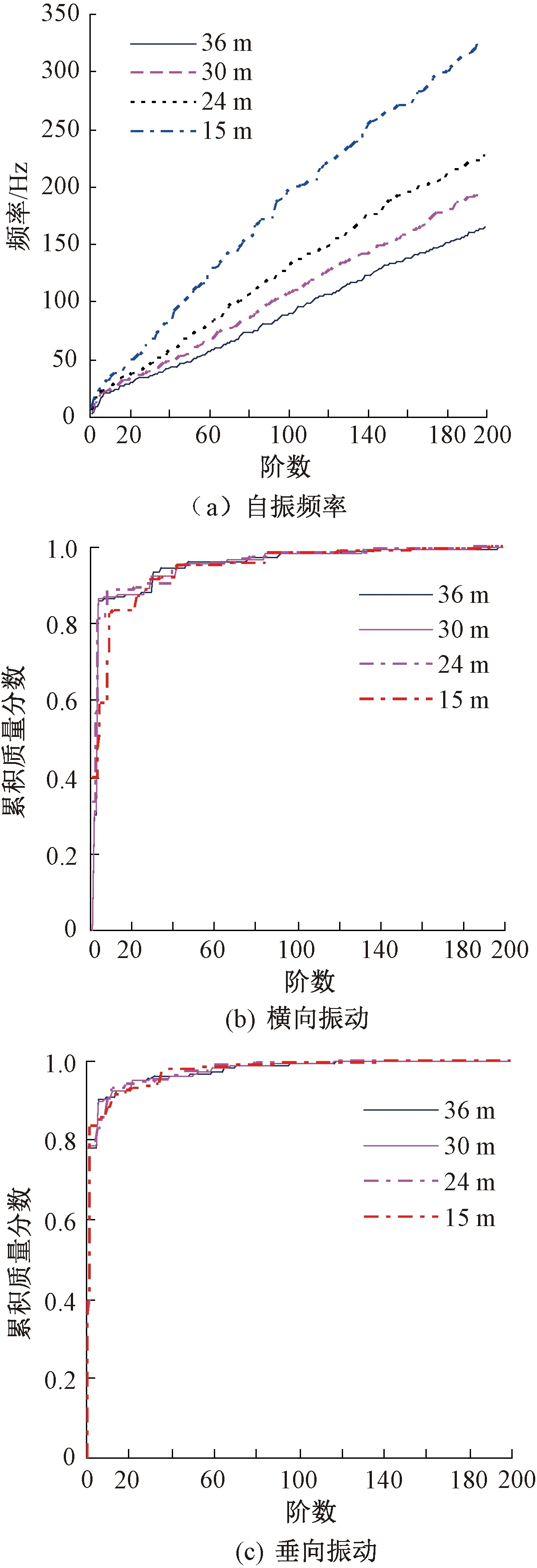
图8 不同净跨高架箱梁的自振特性

图8表明，相同阶次n对应的桥梁自振频率随净跨的增加而减小，这主要是由于桥梁整体刚度随净跨的增加而减小所致；不论是横向振动，还是垂向振动，当阶次达到140时，计算模型的累积质量分数已经达到0.984，说明选择144～250 Hz的上限频率已经满足15～36 m跨径箱梁的振动计算要求，也说明15～36 m跨径箱梁的振动能量主要集中在250 Hz以下。

对30 m净跨的箱梁进行模态分析，分别提取第7、50、93阶次垂向、横向振动的振型，如图9、图10所示。图9、图10表明，当阶次为7、自振频率为20.8 Hz时，箱梁的振动以箱梁整体振动为主；当阶次达到50、自振频率为54.4 Hz时，箱梁的振动开始以局部振动为主，局部振动随阶次的提高逐渐明显。与试验分析结果结合来看，轮轨短波不平顺引起的箱梁振动主要分布在50 Hz以上，以箱梁局部振动为主要表现形式。

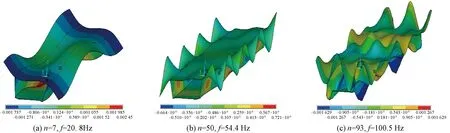
图9 箱梁振型垂向分量(单位：mm)

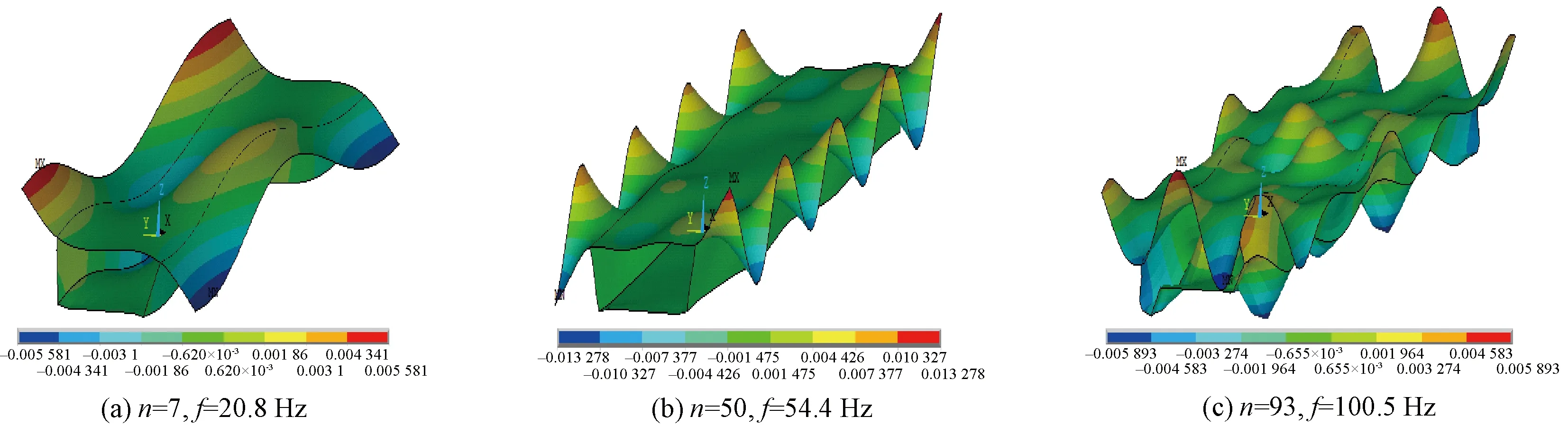
图10 箱梁振型横向分量(单位：mm)

3.2 振动分布特性分析

将列车经过时1/2梁跨断面上各节点的振动时域信号进行1/3倍频程分析，得到该断面上箱梁各部件振动水平的分布图，分别如图11～图14所示。

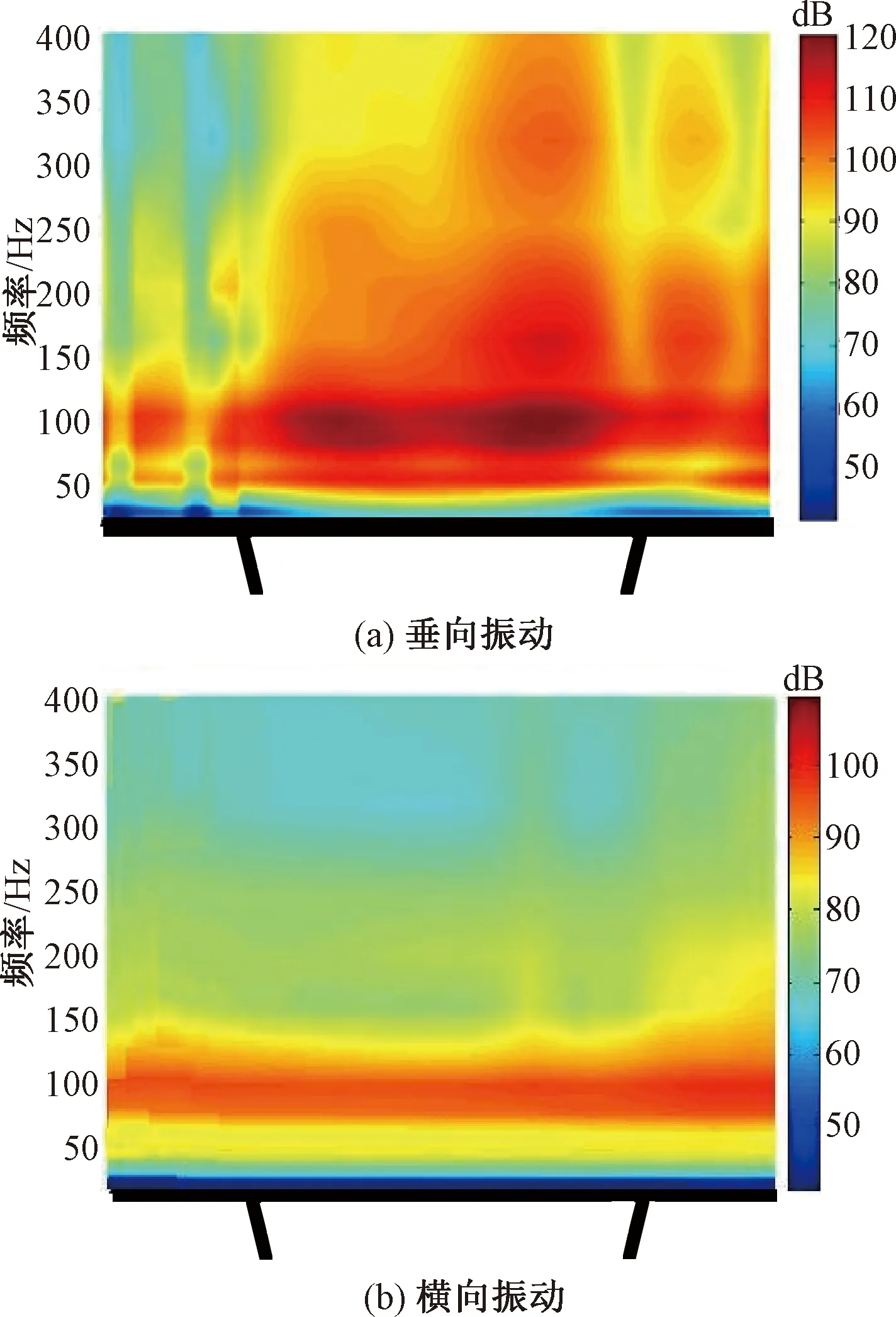
图11 顶板振动水平分布

通过对图11的分析，可以得出：

(1)腹板内侧区域的顶板垂向振动主要分布在40～200 Hz范围内，在63～160 Hz范围内振动水平维持在115～120 dB，在160～200 Hz范围内振动水平维持在105 dB以上，轨道结构区域的振动水平最高，这主要是由于从轨道结构传递下来的振动还未发生衰减，导致振动水平较其他区域高。

(2)轨道结构近侧的翼板垂向振动主要集中在40～200 Hz范围内，在80～160 Hz范围内振动水平基本处在100 dB以上，最大达到110 dB；由于腹板的支撑作用和与振源距离的增加，轨道结构远侧的翼板垂向振动频率主要分布在80～160 Hz范围内，振动水平也相对较弱，分布在90～100 dB。

(3)箱梁顶板横向振动沿顶板分布比较均匀，振动频率主要分布在50～150 Hz范围内，振动水平基本在85～95 dB，说明在列车垂向荷载作用下，顶板的垂向振动是影响其结构噪声的主要因素。

通过对图12的分析，可以得出：

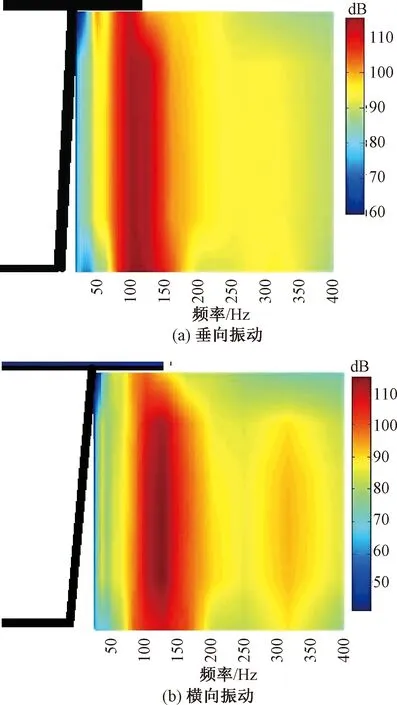
图12 右侧腹板振动水平分布

(1)列车荷载作用下，轨道结构近侧腹板的垂向振动沿腹板位置分布较均匀，主要分布在63～200 Hz范围内，在80～160 Hz范围内振动水平维持在100～110 dB。

(2)由于箱梁的扭转和滞变，轨道结构近侧腹板振动分布较均匀，主要集中在80～200 Hz范围内，振动水平也达到90 dB以上；在100～120 Hz范围内振动水平可以达到110 dB，横向振动与垂向振动同处一个水平，说明在减振降噪分析当中，不能忽略腹板横向振动对桥梁辐射的影响。

图13表明，列车荷载作用下，底板的垂向和横向振动沿底板分布相对均匀，主要分布在60～150 Hz范围内，振动水平处于95～105 dB范围内，垂向振动水平高于横向振动约4 dB。

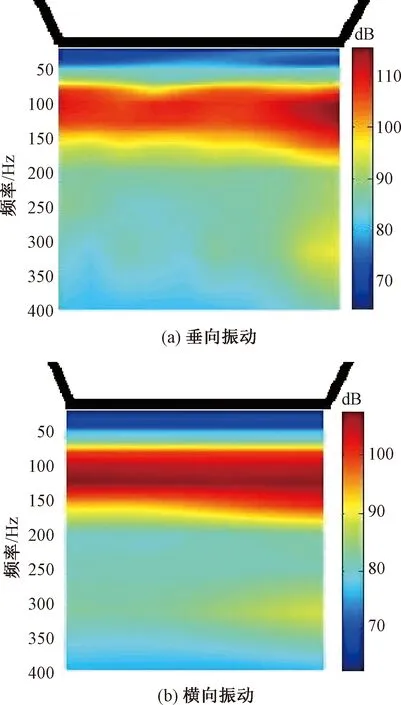
图13 底板振动水平分布

图14表明，列车荷载作用下，轨道远侧腹板的垂向和横向振动主要分布在50～150 Hz范围内，沿腹板位置分布较均匀，振动水平维持在85～100 dB，横向振动与垂向振动处于同一水平，振动水平较轨道近侧腹板小约15 dB。

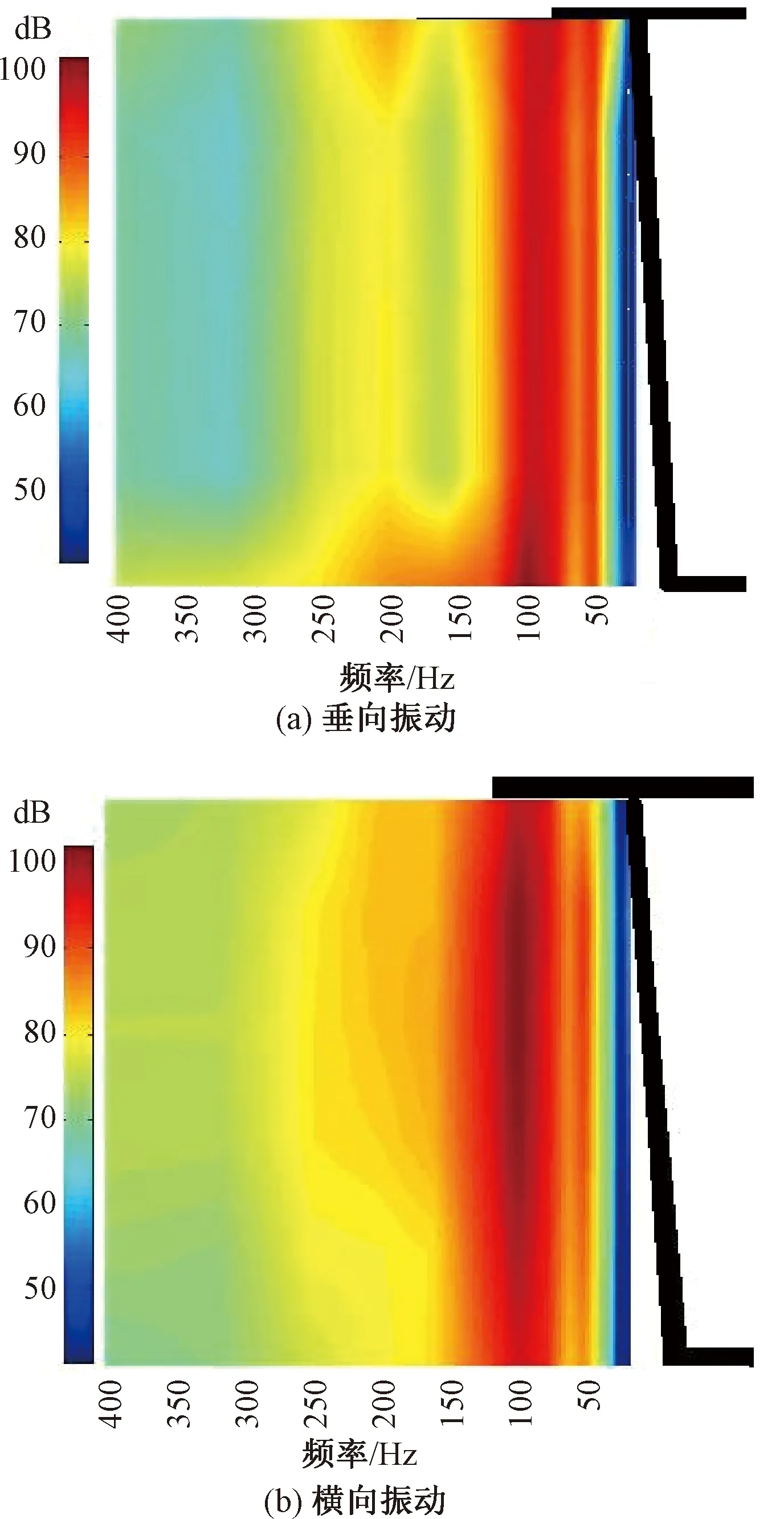
图14 左侧腹板振动水平分布

4 结论

本文利用有限元分析和现场试验对城市轨道交通高架箱梁振动特性进行了分析，重点研究了对桥梁结构辐射噪声具有重要影响的20～200 Hz箱梁振动特性和分布规律，得到以下结论：

(1)实测分析表明，列车荷载作用下，箱梁结构振动主要集中在40～200 Hz范围内，影响箱梁振动特性的主要是波长0.075～0.375 m的轮轨短波不平顺。箱梁顶板轨道中心处垂向振动水平最大，翼板中心、顶板中心、梁底中心依次减小，腹板的垂向振动最小。

(2)模态分析表明，箱梁振动能量主要集中在250 Hz以下，当振动频率大于50 Hz时，箱梁振动以局部振动为主要表现形式。

(3)通过对箱梁振动分布特性分析可知，箱梁顶板的轨道结构区域振动水平最高，轨道结构近侧的翼板振动水平较远侧高，顶板横向振动沿顶板分布比较均匀，顶板和翼板振动的主要形式为垂向振动。箱梁腹板振动沿腹板分布较均匀，主要分布在63～200 Hz范围，轨道结构近侧振动水平处于90～110 dB，轨道结构近侧腹板的振动水平较远侧高约15 dB。腹板的振动水平较顶板等构件低，但腹板横向振动与垂向振动同处一个水平，因此不能忽略腹板横向振动对桥梁辐射噪声的影响。箱梁底板振动沿底板分布相对均匀，主要分布在60～150 Hz范围内，振动水平处于95～105 dB范围内，垂向振动水平高于横向振动4 dB。