标签局部结构保持的离散哈希方法
2022-05-10敖宇翔滕少华滕璐瑶
敖宇翔,滕少华,张 巍,滕璐瑶
1(广东工业大学 计算机学院,广州 510006)
2(Monash University,Melbourne 3800,Australia)
1 引 言
近年来,随着互联网应用展开,文本、图像、视频等不同模态数据和高维度数据迅速增长.多模态、高维度信息检索,尤其是跨模态检索需求大幅度增长.例如,给定一个关于动物的文本查询,人们不满足于仅从文本中检索到该动物的信息,还希望从图像和视频等其他模态中浏览到该动物.这使传统的最近邻搜索无法满足人们的需求,跨模态哈希检索技术因其检索效率高、存储成本低而使其广受关注[1-3].源模态数据转换为二进制哈希码后能大幅度降低存储开销,并且哈希码之间的硬件级异或操作也提高了汉明空间[4,5]中的搜索效率.
早期的许多工作都只关注单一模态[6,7],即查询和搜索结果处于同一模态.近年来,跨模态哈希研究成为热点.跨模态哈希检索又可分为无监督和有监督方法两个大类.
无监督跨模态哈希的重点是利用不同模态数据的特征信息来寻找模态之间的相关性.其中跨模态哈希(IMH)[8]使用模态内和模态间关系来构造亲和矩阵 再利用亲和矩阵学习公共子空间.协同矩阵分解哈希(CMFH)[9]将多模态数据利用矩阵分解,分解为模态特有特征和模态共有特征,再利用共有特征获得哈希码.融合相似度哈希(FSH)[10]首先获取多模态数据之间的相关性并构建融合相似度,然后在汉明空间中保持融合相似度.潜在语义稀疏哈希(LSSH)[11]将稀疏编码和矩阵分解相结合来获取潜在语义特征,然后利用潜在语义特征获取哈希码.
而有监督跨模态哈希方法则使用监督信息(标签)填补模态之间的巨大差异.在有监督的跨模态哈希方法中,语义相关性最大化哈希(SCM)[12]通过标签构造余弦相似度矩阵来学习哈希码.有监督矩阵分解哈希(SMFH)[13]利用标签余弦相似度构建图正则化来约束协同矩阵分解得到的公共特征,从而在生成的哈希码中保持标签相似度.然而上述方法都在学习哈希码的过程中松弛了离散约束,导致可能产生量化误差,降低哈希码的质量[14].离散交叉模态哈希(DCH)[14]构建了一个线性分类框架将哈希码映射到标签矩阵,DCH采用循环坐标下降策略(DCC)[15]逐位更新哈希码,减少了松弛离散约束造成的量化误差.可扩展的离散矩阵分解哈希(SCRATCH)[16]通过集合矩阵分解和语义嵌入来学习一个潜在的语义空间,然后利用潜在语义空间离散生成哈希码,减少了较大的量化误差.
近年来,随着深度学习应用展开,一些基于深度学习的跨模态哈希方法开始出现,并且表现不俗,比如:深度跨模态哈希[17],自监督对抗哈希[18],循环一致性深度生成哈希[19]等.
虽然许多跨模态哈希方法已经被提出,并有较好的效果,但仍有一些问题需要探讨:1)一些方法只提取了多模态数据中的信息,而忽略了具有更强语义的标签信息;2)一些方法只将标签信息转化为相似度并嵌入到哈希码中,但这种转化也将引起标签的语义信息损失;3)一些方法没有使用核函数,难以捕捉到源数据间的非线性关系.
针对这些问题,本文提出了一种新颖的跨模态哈希方法——标签局部结构保持离散哈希(LSPDH),不同于其他使用流形学习的跨模态哈希方法,本文方法分为哈希码学习和哈希函数学习两步.哈希码学习中运用流形学习在汉明空间中保持标签信息的局部结构,并将标签信息映射到哈希码矩阵,融入哈希码学习过程,减少了标签信息转化为局部保持图约束所造成的语义信息损失;哈希函数学习中使用了核函数来获取数据间的非线性关系.最后,通过实验验证了本方法的有效性.
本文组织如下:第2节提供了相关工作的概述,第3节阐述了所提出的方法,第4节是实验的详细描述和综合分析,最后在第5节中给出了结论.
2 相关工作
本节将介绍一些与LSPDH相关的研究,主要包括流形学习在哈希学习中的应用和两步哈希学习.
2.1 流形学习在哈希学习中的应用
流形学习自提出以来就受到了广泛的关注.近年来哈希学习的一些研究结果表明,保持流形结构可以有效地提高哈希码的质量.流形学习的应用首先从单模态哈希检索开始.谱哈希(SH)[6]希望在汉明空间中距离较大的两个数据点在源数据空间中具有较小的相似度,它将流形学习转化为Laplace-Beltrami特征函数,通过简单的阈值操作得到哈希码.在此基础上,锚点图哈希(AGH)[20]被提出来了,它利用锚点将邻接矩阵替换为近似邻接矩阵,降低了时间复杂度.此外,还有其他使用流形学习的哈希方法,如离散图哈希(DGH)[21]和离散多视图哈希(DMVH)[22].
上述方法只能在单一模态下工作.近年来,在跨模态哈希检索领域,流形学习的使用也开始变得频繁起来,例如,跨模态哈希(IMH)[8]通过结合模态间一致性和模态内一致性来学习哈希码.监督矩阵分解哈希(SMFH)[14]利用标签信息来计算余弦相似矩阵,并结合协同矩阵分解生成哈希码.融合相似度哈希(FSH)[10]构造一个融合图来定义多模态数据之间的相似度,然后在汉明空间中保持融合相似度.此外,还有其他使用流形学习的交叉模态方法提出[23].但是,上述方法和本文方法有很大的不同.上述方法大部分利用流形学习提取原始数据的特征,而本文方法则利用流形学习提取标签信息的特征,在汉明空间中保持标签信息的局部结构.
2.2 两步哈希学习
早期跨模态方面的研究都是采用一步哈希的学习策略.近年来的一些研究[24,25],将哈希学习分解为两个步骤:1)哈希码学习;2)哈希函数学习.该学习策略使哈希学习过程更加高效和灵活,从而影响了很多研究.语义保持哈希(SEPH)[24]为哈希码的每一位学习一个核逻辑回归函数,但这会增加大量时间消耗.两步跨模态哈希(TECH)[25]在哈希函数学习的过程中加入了相似度保持.其他一些方法则是使用简单的线性回归来学习哈希函数[23].将哈希学习过程分解为两步,可以将哈希函数学习视为一个分类任务,可以在哈希函数学习中使用更复杂、更强大的模型.与此同时,使用过于复杂的模型会显著增加训练时间[24].在本文中,将使用核回归函数作为哈希函数.
3 提出方法
本文方法基于如下直观知识:如果两个样本数据(文本、图像、视频等)共有的标签类别数越多,代表其描述的内容相似性越高,为使变换不丢失原有标签信息,因而,要求变换后样本数据的汉明空间距离也应该保持相近.基于此,本文思路如下:样本数据共有的标签数越多,其描述的内容相似度越高,汉明空间应距离越相近,最后,生成的哈希码的相似性也应越高.由此,本文方法在哈希码学习过程中,尽量保持数据的标签信息不变,其示意图如图1所示.

图1 LSPDH示意图
为便于描述,本文中使用的符号在此统一给出.
3.1 符号

3.2 哈希学习
针对多模态哈希检索现存的问题,本文提出一个基于标签局部结构保持的离散哈希方法,分为哈希码学习和哈希函数学习两步,详述如下:
3.2.1 哈希码学习
1)标签信息局部结构保持
许多方法利用流形学习在汉明空间中保持多模态数据的结构特征.本文的方法则尽量在汉明空间保持数据的标签信息不变,这符合检索目标.因此,采用Locality Preserving Projection(LPP)[26]的思想构造流形相似度矩阵来保持标签信息的局部结构:
(1)
如上所示,首先需要找到每个样本数据的K个最邻近点, 如果Yi是Yj的一个邻近点,或者Yj是Yi的一个邻近点(K个最邻近点之一),则在这两个点之间的边上赋予一个热核权值(其权值与距离成反比),否则这个权值为0,式(1)中t为宽度参数,本文设置为1.在计算完流形相似度矩阵之后,使用它来构建图约束,以此在汉明空间中保持标签信息的局部结构.然而,由于哈希码具有离散性, 在直接约束哈希码之后,哈希码的优化求解将很难进行.解决方法是在潜在空间V上施加约束,并让它近似哈希码矩阵B:
s.t.B∈{-1,1}k*n
(2)

2)标签线性映射
利用投影矩阵把标签矩阵直接映射到哈希码矩阵B,以此减少构建相似度矩阵所造成的语义信息损失,并使哈希码包含更多语义信息:
(3)

3)整体目标函数
s.t.B∈{-1,1}k*n
(4)
其中α,β为权重参数,分别控制了流形学习和标签线性映射对方法效果的影响.
4)优化算法
显然,直接优化具有3个变量(B,V,Q)的非凸目标函数是很困难的.然而,如果每一次只优化一个变量,然后固定住其他变量,这就变成一个凸优化问题.因此,采用迭代优化策略更新B,V,Q来获得一个近似解.
更新B:固定V,Q,更新B.目标函数式(4)可写为如下形式:
s.t.B∈{-1,1}k*n
(5)
将式(5)展开:

(6)
第1项(β+1)tr(BTB)为常数项,将它和与B无关的项舍去可得:
(7)
=-tr((VT+βYTQT)B)
s.t.B∈{-1,1}k*n
(8)
最终,可以在保持离散约束的同时得到B矩阵的优化结果:
B=sgn(V+βQY)
(9)
更新V: 固定B,Q,更新V.抛弃与V不相关的项, 可以将目标函数式(4)写为:
(10)
令式(10)对V的导数为零,则有等式:
-2B+2V+αV(L+LT)=0
(11)
V=2B(2I+α(LT+L))-1
(12)
更新Q:固定B,V,更新Q.类似于更新V,留下和Q相关的项:
(13)
令式(13)对Q的导数为零,则有等式:
-2BY’+2QYY’=0
(14)
Q=BYT(YYT)-1
(15)
为了得到式(4)的最终局部最优解,可以使用迭代更新策略,通过上述步骤更新B,V,Q,直到它们收敛.
3.2.2 哈希函数学习
如前所述,LSPDH为两步哈希方法.哈希码学习所得到的哈希码矩阵B是用于检索的数据库.对于样本外的数据,需要为它们学习哈希函数,将它们映射到汉明空间.为了捕捉数据间的非线性特征,本文采用核回归作为哈希函数,可以使得一些低维线性不可分的数据映射到高维后线性可分.t模态的目标哈希函数如下:
(16)

Pt=Bφ(Xt)T(φ(Xt)φ(Xt)T+λI)-1
(17)
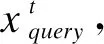
(18)
算法1总结了哈希码学习和哈希函数学习的整个优化过程.
算法1.LSPDH的优化算法
输入:训练集Xt;标签值Y; 参数α,β,λ.
输出:哈希码B;哈希函数Pt.
1.将训练集映射到核空间;
2.随机初始化V,Q, 将B的值全部赋为-1;
3.迭代
4.根据式(9)更新B;
5.根据式(12)更新V;
6.根据式(15)更新Q;
7.直到式(4)收敛或达到最大迭代次数;
8.根据式(17)学习哈希函数Pt;
9.返回哈希码B和哈希函数Pt.
3.3 复杂度分析
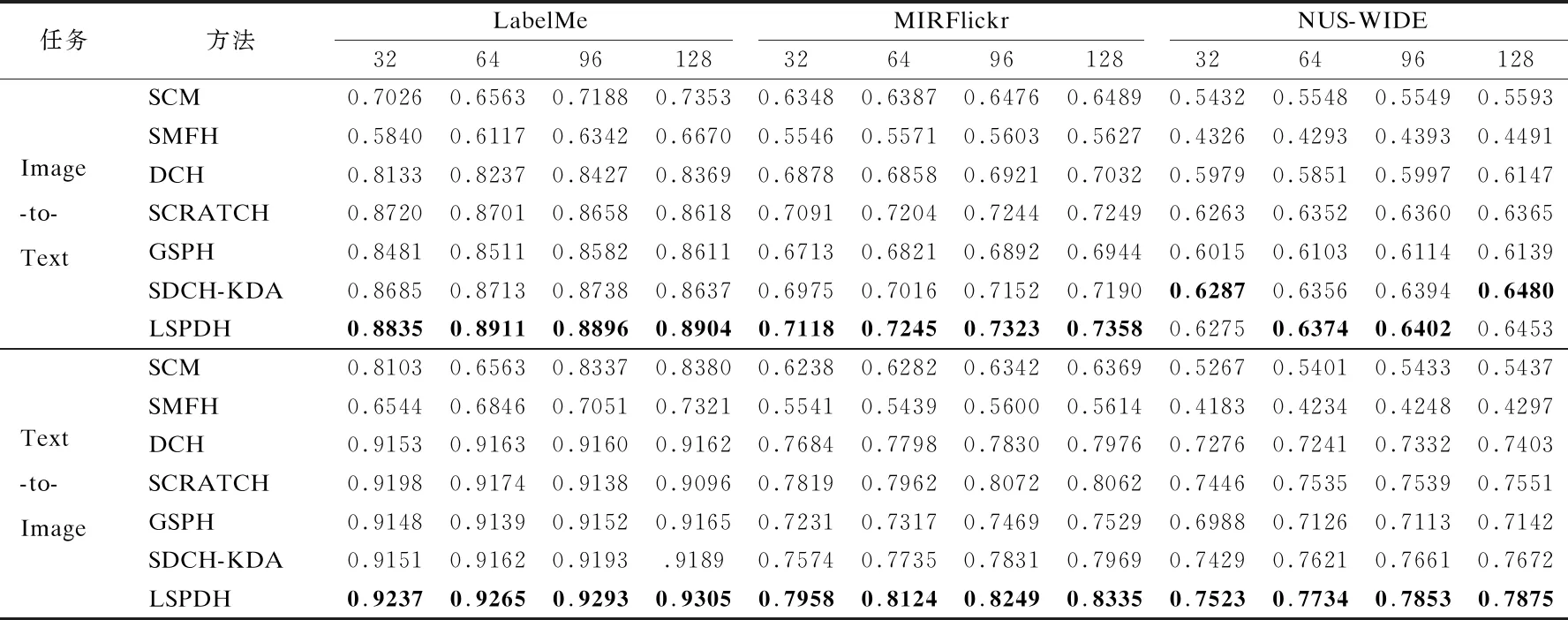
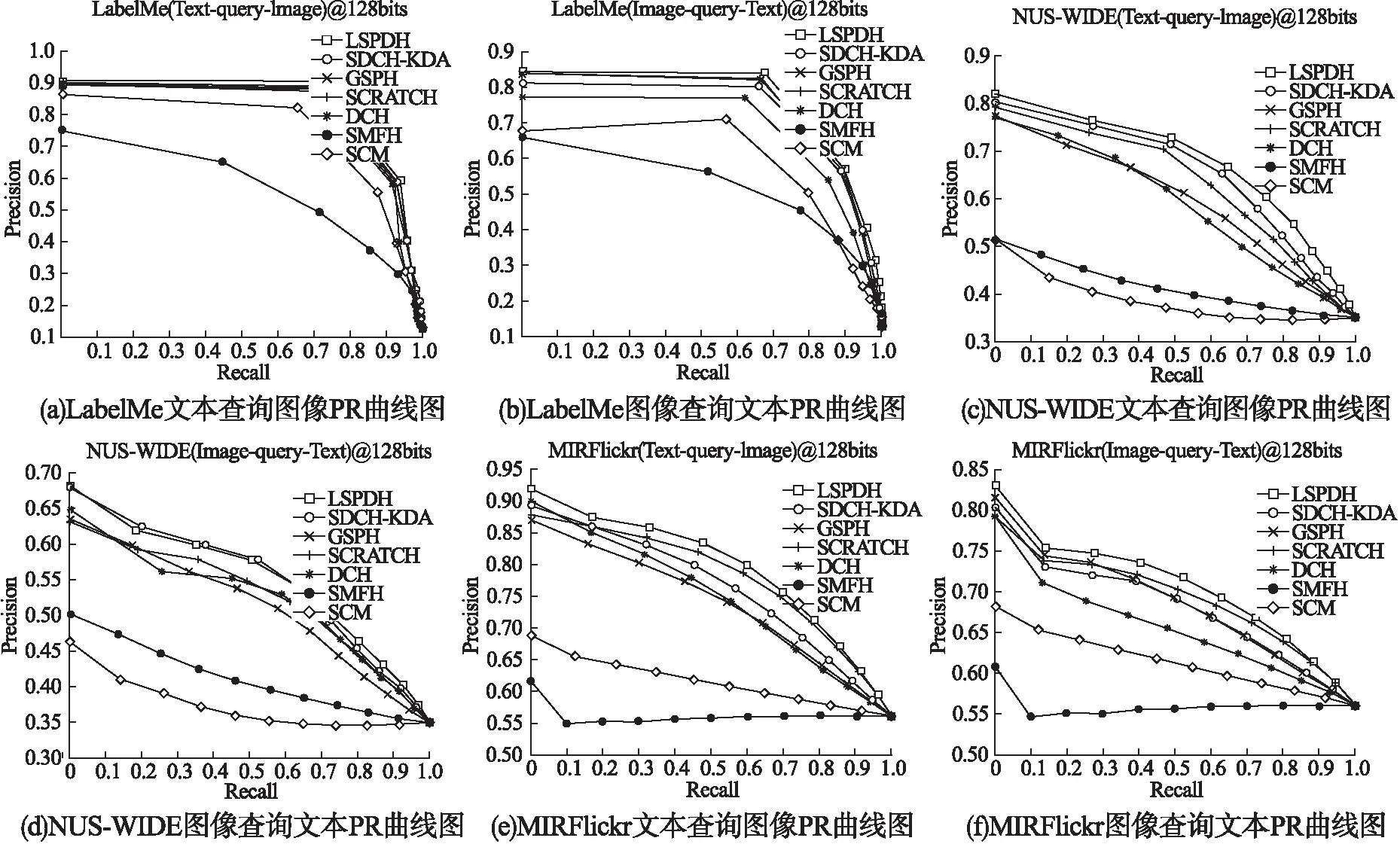
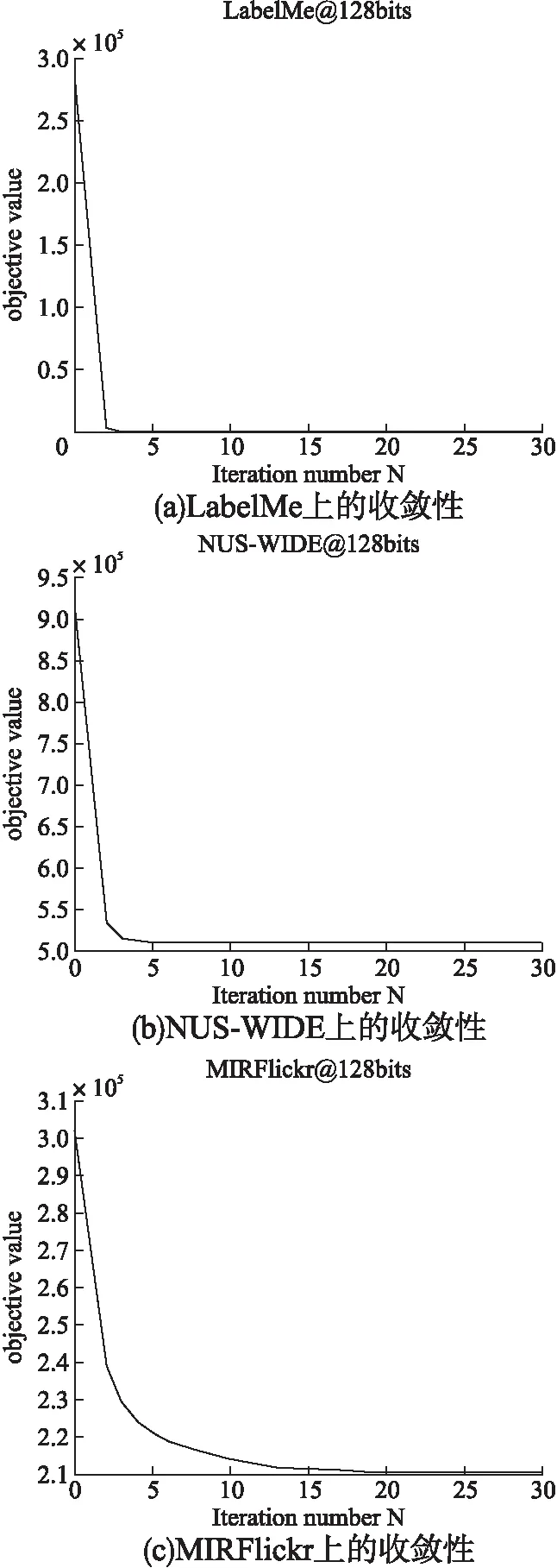
式(9)和式(15)的时间复杂度分别为O(kn+kln)和O(knl+l2n+l3+kl2).式(16)的时间复杂度为O(d2+d2k+d2n+dkn),k为哈希码长度,n为训练数据个数,l为类别总数,d表示使用φ(·)后的特征维数.由于k,l< 在3个基准数据集上进行了充分实验,并与6种近期跨模态哈希方法进行了比较,验证了本文提出的跨模态哈希方法的有效性.所有实验都是在Intel Core I5-8300H CPU和16GB RAM平台上进行. LabelMe[28]:数据集包含2688个图像-文本样本对.数据集中有8个类别,每个样本对都属于其中一个类别.文本用245维词频特征向量表示,图像则用512维Gist特征向量表示.在这个数据集中,随机选取2016个样本对作为训练集,剩下的672个样本对作为测试集. MIRFlickr[29]:它包含了从Flickr网站上下载的25000个图像-文本样本对.每个样本对都用24个标签中的一个或多个标签进行标记.图像通过PCA降维后用150维的边缘直方图特征向量表示,对应的文本也通过PCA降维后用500维的特征向量表示.随机选取5%的样本对作为查询集,其余的作为训练集. NUS-WIDE[30]:它由从Flickr抓取的269,648个图像-文本样本对组成.每个样本对至少有一个或多个标签.数据集的所有样本对可分为81类.由于原始数据集中部分类别样本对较少,因此选择样本对数量最大的10个类别作为实验数据集,共186577个样本对.在每个实例中,图像用500维的视觉词袋 SIFT直方图特征向量表示,对应的文本用1000维的索引特征向量表示.为了减少计算量,在NUS-WIDE中随机选择5000个训练样本对和1867个测试样本对来训练和测试所有的方法. 将本文方法与6种近期的跨模态哈希方法进行了比较.分别是SCM,SMFH,DCH,SCRATCH,GSPH,SDCH-KDA. SCM[13]利用标签信息构造成对相似度矩阵,采用松弛离散策略来生成哈希码,本文使用SCM_seq版本. SMFH[14]构建了一种新的哈希协同矩阵分解框架,并利用图正则化来提高哈希码的质量. DCH[12]构建了一个线性分类框架,并采用DCC离散优化策略减少量化误差,提高哈希码的质量. SCRATCH[15]结合了集体矩阵分解和语义嵌入,以保持模态内和模态间的相似性,并离散生成二进制代码. GSPH[31]在不同场景下,利用数据点之间的相似性学习哈希码,同时为哈希码的每一位学习一个核逻辑回归模型. SDCH-KDA[32]将核判别分析(KDA)整合进离散哈希框架,提高了哈希码的判别能力. 所有对比方法的源代码都是公开的.在实验中设置了两个任务,一个是图像查询文本任务,另一个是文本查询图像任务.在NUS-WIDE, MIRFlickr数据集上α=3,β=5,μ={0.035,0.3},在LabelMe数据集上α=3.5,β=3,μ=0.035. 为了评价各方法的性能,采用了检索领域常用的评价指标:平均精度均值(mAP).在计算mAP之前,需要计算平均精度(AP).给定一个查询q和一个检索到的实例列表R,q的AP定义如下: (19) 其中N是检索集中与q真实相关的实例个数,n检索到的实例列表R的大小,δ(r)=1表示第r个被检索到的实例与查询q相关,否则δ(r)=0,precision(r)表示被检索到的第r个实例的精度.最后对所有查询实例计算AP值,再进行平均就可以得到mAP.此外还将采用precision-recall曲线作为评价指标.在所有的评价指标中,评价指标值越大代表效果越好. 表1总结了LSPDH和对比方法在3个数据集上的mAP值.从表1中可以得出如下结论: 表1 各方法在3个数据集上的mAP值 1)LSPDH的表现在文本查询图像任务中要优于所有对比方法,在NUS-WIDE数据集图像查询文本任务中,32和128比特位上略弱于SDCH-KDA,这表明了LSPDH的有效性. 2)在LabelMe数据集32位图像查询文本和文本查询图像任务中,LSPDH的mAP对比最优方法分别提升约1.1%、0.3%,而在128位下提升分别约为2.7%、1.2%.在MIRFlickr数据集32位同任务中,mAP分别提升近0.2%、1.4%,128位下分别提升近1.1%、2.7%.在NUS-WIDE数据集上,文本查询图像任务下32位提升约为0.9%,128位下提升约为2%,而图像查询文本任务下则和最优方法差距在0.3%以内.可以看出LSPDH在文本查询图像任务中表现更佳,在图像查询文本任务中则表现一般,特别是在NUS-WIDE上,表现与SDCH-KDA相似,这可能因为,文本相对于图像可以更好描述实例,同时文本特征向量和标签向量在结构上也有一些相似之处,例如一段描述汽车的文本,它里面的某些表述可能就是这个文本的标签. 3)LSPDH在32位图像查询文本任务和文本查询图像任务中,平均提升很低,分别约为0.4%、0.8%,而在128位同任务下,平均提升分别约为1.3%、2%.可能的原因是低位数哈希码包含的语义信息不足所导致的.此外可以发现,大部分方法的性能会随着哈希码的位数增加而增加,其原因是更长的哈希码可以包含更多的信息. 图2展示了LSPDH和对比方法的precision-recall曲线,理论上,方法的mAP值越高,其precision-recall曲线也会越高.从图2中可以得出如下结论: 图2 LSPDH与对比方法的precision-recall曲线图 LSPDH基本上高于所有对比方法,在NUS-WIDE图像查询文本任务上表现和SDCH-KDA相似,这与表1的观察结果是一致的. 综上所述,LSPDH与一些先进的方法相比表现出了良好的性能,说明LSPDH可以学习到更加精确的哈希码. 图3显示了目标函数值在3个数据集上随迭代次数的变化曲线.如图3所示,LSPDH可以快速收敛.在NUS-WIDE和LabelMe数据集上,可以观察到LSPDH在5次迭代中收敛,而在MIRFlickr数据集上,它在15次迭代中收敛.这说明本文提出的方法在大多数据集上的训练是有效率的. 图3 收敛性分析 本节进行了参数敏感性分析实验来分析各参数(α,β和μ)的变化对mAP的影响.参数α控制流形学习在方法中的影响程度,参数β控制标签线性映射在方法中的影响程度,参数μ控制正则化项的惩罚程度.在测试每个参数的同时保持其他参数不变.3个参数的变化曲线如图4所示.从图4中可观察到,本文方法可以在参数(α,β和μ)较大范围内表现良好,同时可以观察到α和β分别在 [1e-3,1],[1e-2,10]范围内变化的时,mAP值有比较明显的提升,这表明流形学习和标签线性映射对提升哈希码的质量是有效的.对于单个参数来说,β对mAP的影响大于α,这说明标签值所包含的语义信息非常重要.对于μ,可以看出,它的值不宜过大或过小,过大会导致欠拟合,而过小会导致过拟合,对于不同的模态,其μ值可能不同.综上所述,本文方法α设置在[0.1,10]之间,β设置在[1,10]之间,μ设置在[1e-2,1]之间. 图4 参数敏感性分析 在MIRFlickr数据集上进行了时间消耗实验来对方法复杂度做进一步分析,结果如表2所示.从表2中可以看出,构建图约束的方法(LSPHS)由于时间复杂度为O(kn2),会比时间复杂度为O(n)的方法(SCRATCH)花费更多的时间.此外可以观察到,采用DCC策略学习哈希码的方法(DCH)时间消耗也非常的高,这是因为每一次迭代优化过程中都要逐位学习哈希码.GSPH由于为每一比特位学习了一个核逻辑回归模型,因此GSPH的时间复杂度会随着哈希码位数的增长而显著提升.SDCH-KDA需要计算散度矩阵,在使用了核函数后,SDCH-KDA的时间成本也会明显上升.本文所提出的方法时间消耗较高,其主要原因是LSPDH在MIRFlickr数据集上需要迭代15次,而其他两个数据集只需迭代5次. 表2 各方法在MIRFlickr-5k上的训练时间成本(单位:秒) 本文提出了一种新颖的有监督跨模态哈希方法,命名为标签局部结构保持的离散哈希,简称LSPDH.LSPDH是一个集哈希码学习与哈希函数学习的两步方法,第1步,该方法计算标签相似度矩阵并在潜在空间构建图约束来保持标签的局部结构,再使用标签线性映射降低构建流形相似度所造成的语义损失,使哈希码包含更多的语义信息,因而具有更高的质量;第2步,在哈希函数学习中加入了核函数,用于获取源数据间的非线性信息.LSPDH在3个基准数据上的实验结果表明其性能基本优于近期跨模态哈希方法.在未来的工作中,将考虑保持标签语义的同时,解决使用图约束导致时间复杂度过高的问题,结合深度学习进一步研究跨模态哈希方法.4 实验与结果分析
4.1 数据集
4.2 对比方法及其简介
4.3 评价指标
4.4 实验结果分析
4.5 收敛性分析
4.6 参数敏感性分析

4.7 时间成本分析

5 结束语
