基于专家协同过滤与混合策略的推荐算法

李伟豪

摘要：随着互联网技术和数字媒体的不断发展，因为信息资源过载使用户很难找到自己喜欢的物品，而推荐系统能有效处理该问题。文章针对推荐系统中存在常见的噪声用戶和冷启动问题，提出了基于专家用户协同过滤和奇异值分解（SVD）的混合推荐算法。先对用户进行专家用户人工筛选降噪，再利用SVD算法分解后填充专家评分矩阵，同时在计算用户与专家的相似度时加入时间权重，最终选择最优项目进行推荐。最后使用MovieLens数据集将本文算法与传统算法进行实验分析对比，证明了该算法的有效性。

关键词：推荐系统;专家用户;SVD;冷启动;噪声用户;混合推荐算法

中图分类号：TP391.3      文献标识码：A

文章编号：1009-3044（2022）09-0054-04

1引言

随着互联网信息量不断增长以及大数据时代的到来，这对每个人的生活都带来了影响，为了应对海量的信息光有普通的搜索引擎在很多时候是达不到用户的个性化需求的。推荐系统在处理信息过载[1]的问题时会有较好的效果。推荐系统通过大数据分析、学习出用户的偏好，然后推荐用户大概率会喜欢的物品。时至今日，在很多的领域都能看见推荐系统[2，3]的身影。

协同过滤推荐[4，5]（Collaborative Filtering， CF）是众多经典推荐算法中的一类。其中基于用户的协同推荐算法[6]（User-based CF，UCF）其思想是先计算出用户之间的相似度，按照相似度大小由高到低排列该用户的邻居集合，再依据得到的邻居集合来计算出各自评分来推测该用户可能会喜欢哪个物品;基于物品的协同推荐算法[7]（Item-based CF，ICF）其思想是先计算出物品之间的相似度，然后依据相似度大小由高到低排列出相似物品集，最后把排在前面的相似度高的物品推荐给用户。但传统的CF算法中无论是ICF或是UCF，在面对现实世界的稀疏评分矩阵或是噪声用户的影响时，其效果往往不理想。后来Le[8]等人提出了奇异值矩阵分解方法（singular value decomposition，SVD），该方法通过降维特征分解原始评分矩阵，然后在召回阶段由稀疏矩阵推算出其他的空缺评分。

但SVD也存在一些问题。举个例子，如果有1万个用户和1000万条物品的评分矩阵，我们简单估计下它需要的内存。假设每个评分用4个字节表示，如果采用SVD分解，将这个完整的矩阵加载到内存中，大概需要372G内存。这对内存有一定要求。而通过提取专家用户评分矩阵可以有效缓解这一问题，且专家用户评价的物品类型广，一些冷门的物品也会进行评价，由此有效缓解了冷启动问题。同时因为每位专家用户的评价数量大，能给出更加客观的评分，能对评分有效降噪。因此，本文提出了基于SVD模型和专家用户协同过滤的混合推荐算法（SVD-ECF），算法首先设置阈值挑选专业影评人，组成专家评分矩阵，然后利用SVD技术对原始评分矩阵进行降维分解之后，利用随机梯度下降法[9]学习并填充空白评分，得到近似评分矩阵，在计算用户与专家的相似度时加入时间权重，挑选出与用户相似的专家近邻，最终基于专家近邻对物品评分的高低进行推荐。

2相关工作

2.1协同过滤推荐算法

普通的协同过滤推荐算法普遍采用了KNN算法[10]预测用户评分。这种算法原理是：首先找出k个最近邻居（可以是基于用户，也可以是基于物品），预测出用户对物品的评价。再依据预测的评价得分高低排列出推荐列表。协同过滤算法可被分为基于用户的协同过滤算法（UCF）和基于物品的协同过滤算法（ICF）。本文主要是对UCF以及SVD进行混合和改进，ICF就不是本文的重点了。

2.1.1基于用户的协同过滤算法

“物以类聚，人以群分”这句俗话能较为形象的描述UCF的原理。在基于用户的协同过滤算法中用户集为U={u，u，u，...，u}m表示用户数量，物品集为I={i，i，i，...，i}n表示物品数量，二者构成一个R[m×n]的用户评分矩阵，根据这个评分矩阵计算并找出用户的相似邻居，关于相似度的计算采用的是常见的皮尔森相关性的相似度计算法[11]，方法如下：

2.3 专家用户

专家用户的概念在2009年由Amatriain等人提出[14]。专家用户的定义如下：某个领域，他们能客观的给出深思熟虑的、波动小的、有理有据的评价（打分）。不同于普通用户集的噪声大，专家在评分时候更加客观、公正，使得物品的评分反映更加真实;而且因为专家是专业影评人，很多冷门物品也会评价，无论他本人是否关注这类物品，如此一来能有效缓解新物品的冷启动问题;除此之外专家评分数据相较于普通用户评分数据更加的稠密。在现实生活中，相较于普通用户的推荐，大家更乐意听取权威的专家推荐。国内的著名电影网站豆瓣猜也充分利用了专家用户这种思想。

3基于SVD模型和专家用户协同过滤的层叠式推荐算法

3.1寻找专家

首先设置一个阈值α，依据数据集里的用户—项目评分矩阵计算出每个用户评分总数，然后按照评分数目总数从大到小依次排序，剔除掉总评分数目小于预定阈值α的用户们，最终剩下的用户们则组成专家用户集。

3.2改进基于用户相似度计算

目前，有关基于用户的相似度的计算方法大多数都没有考虑引入一个时间权重，而在现实世界中，人们感兴趣的点往往会跟随时间改变。比如很多孩子年少时爱看青春偶像剧，长大后可能更爱看家庭剧。如果还是按照很久以前用户的喜好进行推荐，结果很可能不如人意。一个实用的推荐系统应该推荐给用户他们现在需要的东西，或者现在正感兴趣的东西。出于这样的考虑，本文决定在基于用户之间的相似度计算时，引入时间权重。使得最近评价过或者购买过的物品有着较高的权重，很久以前评价过或者购买过的物品有着较低的权重。

基于上述讨论，本文将利用指数函数来设计遗忘函数，用来表示时间变化量对用户喜好的影响程度[15]：

3.3基于SVD模型和专家用户协同过滤的层叠式过滤推荐算法及模型

在实际进行推荐的过程中，现实世界噪声用户多且传统协同过滤算法会遇到数据稀疏以及冷启动等问题，这些问题都会影响到最终的推荐结果质量。本文提出一种基于SVD模型和专家用户协同过滤的混合推荐算法：首先对用户数据集进行筛选，设置一个阈值α，只留下评分总条目个数大于等于α的专家用户。然后对剩下的项目评分矩阵A使用SVD矩阵分解技术得到三个矩阵分别为U、S、V，再对对角矩阵S进行降维处理，并得到对应的降维后的用户矩阵U和项目矩阵V。 再用随机随机梯度下降法填充得到最终的近似矩阵R。最后在近似矩阵R中加入时间权重改进用户与专家的相似度计算公式，得到预测评分P′。如此一来利用SVD技术解决了由传统协同过滤算法的数据稀疏性问题带来的预测效率低问题，专家用户有效缓解冷启动等问题，减少了噪声用户。同时也弥补了SVD矩阵分解带来的解释性不强等问题，提高了精度。具体算法描述如下：

输入：用户项目评分数据集

4实验结果和分析

4.1实验数据

本文采用Movielens数据集[16]，此数据集由美国明尼苏达大学的Grouplens实验室提供，此数据集是十分经典的用户电影评分数据集。本数据集里有100 004条评分、943位用户、以及9743个电影，其中每位用户至少评价过20部电影。用户评分范围为1∼5分，0分表示未对该电影进行评价，评分等级分为10级，间隔区间为0.5。

4.2评价标准

通过对比算法的预测评分与真实评分能评价出一个算法的好坏，在需要向用户展示预估评分时这个指标尤为重要。预测评分准确度的指标有很多，本质上都是比较算法预测评分与实际评分的差值大小。如果预测评分与真实评分的差值大，那么推荐系统的精确度就低，反之推荐系统的精确度就高。本文将采用较为经典的平均绝对误差（Mean Absolute Error，MAE）与准确性（precision）[17]来衡量SVD-ECF算法的精确性。

4.3实验结果分析

4.3.1 参数分析

1）阈值α的选取

首先我们对Movielen数据集上所有用户进行了评分数量统计，如图1所示。

由图1可以看出用户的评分数量集中在50条至250条，只有大约100多人能够对电影评价超过250条。

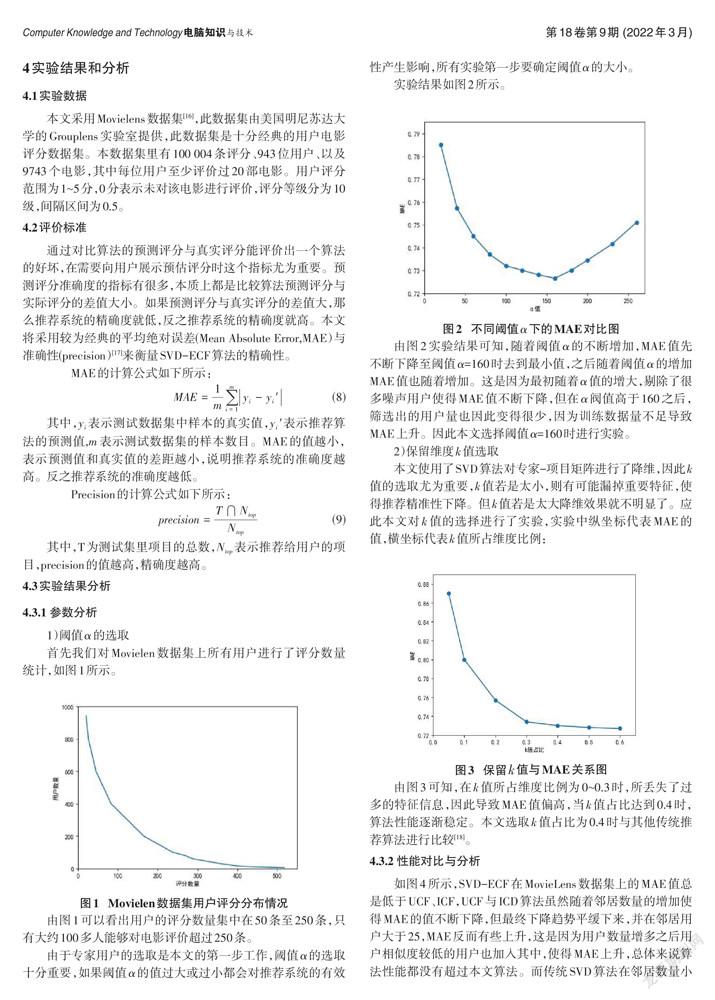
由于专家用户的选取是本文的第一步工作，阈值α的选取十分重要，如果阈值α的值过大或过小都会对推荐系统的有效性产生影响，所有实验第一步要确定阈值α的大小。

实验结果如图2所示。

由图2实验结果可知，随着阈值α的不断增加，MAE值先不断下降至阈值α=160时去到最小值，之后随着阈值α的增加MAE值也随着增加。这是因为最初随着α值的增大，剔除了很多噪声用户使得MAE值不断下降，但在α阀值高于160之后，筛选出的用户量也因此变得很少，因为训练数据量不足导致MAE上升。因此本文选择阈值α=160时进行实验。

2）保留维度k值选取

本文使用了SVD算法对专家-项目矩阵进行了降维，因此k值的选取尤为重要，k值若是太小，则有可能漏掉重要特征，使得推荐精准性下降。但k值若是太大降维效果就不明显了。应此本文对k值的选择进行了实验，实验中纵坐标代表MAE的值，横坐标代表k值所占维度比例：

由图3可知，在k值所占维度比例为0∼0.3时，所丢失了过多的特征信息，因此导致MAE值偏高，当k值占比达到0.4时，算法性能逐渐稳定。本文选取k值占比为0.4时与其他传统推荐算法进行比较[18]。

4.3.2 性能对比与分析

如图4所示，SVD-ECF在MovieLens数据集上的MAE值总是低于UCF、ICF，UCF与ICD算法虽然随着邻居数量的增加使得MAE的值不断下降，但最终下降趋势平缓下来，并在邻居用户大于25，MAE反而有些上升，这是因为用户数量增多之后用户相似度较低的用户也加入其中，使得MAE上升，总体来说算法性能都没有超过本文算法。而传统SVD算法在邻居数量小于15时MAE低于本文算法，但随着邻居数量增多，SVD-ECF表现比传统SVD算法好。但仅仅依靠一个评估标准不能完全确定一个推荐系统的好坏，因此本文采用precision指标继续进行对比。

如图5所示，随着邻居数量增加，UCF与ICF的精确性持续上涨，在邻居数量达到30时，上涨趋势明显变缓，最终没能超过SVD和本文算法，而SVD-ECF与SVD在k值占比都为0.4时，SVD-ECF当邻居个数大于20之后精确度更高。 结果表明，SVD-ECF算法显然能够获得比其他传统算法更好的推荐结果。

5结论

本文针对现实世界中噪声用户过多，传统过滤算法会受到数据稀疏、冷启动等问题的影响，提出了一种基于SVD模型和專家用户的层叠过滤推荐算法，该算法通过设置阈值挑选专家用户，然后使用SVD算法分解专家-项目评分矩阵，并加入时间权重优化相似度计算。实验证明本文算法能够有效提高推荐准确度。SVD算法需要进行矩阵分解，计算复杂度高，在大规模的数据上，SVD分解会降低程序的速度。SVD分解可以在程序调入时运行一次。在大型系统中，SVD每天运行一次或者其频率更低，并且还要离线运行，专家集正好精炼了数据集，且有效缓解了噪声与冷启动问题。但本文算法需要大量专家用户的数据，能否保护用户的隐私的同时收集数据是之后的工作需要解决的问题。

参考文献：

[1] 蔺丰奇，刘益.信息过载问题研究述评[J].情报理论与实践，2007，30（5）：710-714.

[2] Kunaver M，Požrl T.Diversity in recommender systems - A survey[J].Knowledge-Based Systems，2017，123：154-162.

[3] 刘建国，周涛，汪秉宏.个性化推荐系统的研究进展[J].自然科学进展，2009，19（1）：1-15.

[4] Fu M S，Qu H，Yi Z，et al.A novel deep learning-based collaborative filtering model for recommendation system[J].IEEE Transactions on Cybernetics，2019，49（3）：1084-1096.

[5] Kwon K，Cho J，Park Y.Multidimensional credibility model for neighbor selection in collaborative recommendation[J].Expert Systems With Applications，2009，36（3）：7114-7122.

[6] Zhao Z D，Shang M S.User-based collaborative-filtering recommendation algorithms on hadoop[C]//2010 Third International Conference on Knowledge Discovery and Data Mining.January 9-10，2010，Phuket，Thailand.IEEE，2010：478-481.

[7] 汪從梅，王成良，徐玲.自适应用户的Item-based协同过滤推荐算法[J].计算机应用研究，2013，30（12）：3606-3609.

[8] Le B H，Mori K，Thawonmas R.An extension for bounded-SVD—A matrix factorization method with bound constraints for recommendersystems[J].Journal of Information Processing，2016，24（2）：314-319.

[9] Gemulla R，NijkampE，Haas P J，et al.Large-scale matrix factorization with distributed stochastic gradient descent[C]//Proceedings of the 17th ACM SIGKDD international conference on Knowledge discovery and data mining - KDD '11.August21-24，2011.SanDiego，California，USA.NewYork：ACM Press，2011.

[10] Zhang M L，Zhou Z H.ML-KNN：a lazy learning approach to multi-label learning[J].Pattern Recognition，2007，40（7）：2038-2048.

[11] Dow H E， Li R， Potter T W. Computer-based method： US，1994.

[12] Barragáns-Martínez A B，Costa-Montenegro E，Burguillo J C，et al.A hybrid content-based and item-based collaborative filtering approach to recommend TV programs enhanced with singular value decomposition[J].Information Sciences，2010，180（22）：4290-4311.

[13] ZhouX，HeJ，Huang G Y，et al.A personalized recommendation algorithm based on approximating the singular value decomposition （ApproSVD）[C]//2012 IEEE/WIC/ACM International Conferences on Web Intelligence and Intelligent Agent Technology.December 4-7，2012，Macao，China.IEEE，2012：458-464.

[15] 史艳翠，戴浩男，石和平，等.一种基于时间戳的新闻推荐模型[J].计算机应用与软件，2016，33（6）：40-43.

[16] HarperFM，KonstanJA.The MovieLensdatasets[J].ACM Transactions on Interactive Intelligent Systems，2016，5（4）：1-19.

[17] Herlocker J L，KonstanJ A，Terveen LG，et al.Evaluating collaborative filtering recommender systems[J].ACM Transactions on Information Systems，2004，22（1）：5-53.

[18] 刘晴晴，罗永龙，汪逸飞，等.基于SVD填充的混合推荐算法[J].计算机科学，2019，46（S1）：468-472.

【通联编辑：王力】