地基与库水模型对重力坝地震响应的影响研究
2022-05-09潘子悦陈灯红赵艺园刘云辉
潘子悦 陈灯红 赵艺园 刘云辉
(1.防灾减灾湖北省重点实验室(三峡大学),湖北 宜昌 443002;2.三峡大学 土木与建筑学院,湖北 宜昌 443002)
目前,我国一批特大型混凝土重力坝拟建、正在建设或已建成,这些高混凝土重力坝工程,除了具有规模宏大、效益显著的特点外,另一重要的共同点是它们均处于地震活动频繁的西南地区,大坝抗震设防水平高,抗震设计难度大,国内外少有先例.
国内外对于高坝抗震的研究主要有四个方面[1-3],包括坝址地震动的确定、筑坝材料动态力学特性和破坏机理研究、大坝地震响应分析以及大坝动力安全评价.其中,大坝-地基-库水系统的地震响应分析一直是国内外学者研究的热点.在数值建模中,该系统分为近场部分和远场部分,其中如何精确描述远场截断边界的辐射条件是关键.
在大坝-地基动力相互作用方面,现有求解方法可分为两类,即局部的近似解法和全局的精确解法[4].近似方法包括黏性边界、黏弹性边界、多次透射边界、无限元及其他的高阶边界等,精确方法有边界元法、比例边界有限元法等.目前,用于混凝土坝-库水-地基系统地震响应分析中的主要方法有黏性边界、黏弹性边界和多次透射边界.Chopra[5]采用黏性边界计算了二维、三维混凝土坝-库水-地基系统的地震响应.杜修力等[6]将黏弹性人工边界结合显式有限元的时域波动求解方法用于小湾拱坝-地基开放系统的地震响应分析.刘云贺等[7]建立了拱坝地震自由场输入模型,比较、验证了黏性边界和黏弹性边界的吸能效果.张楚汉等[8]考虑了无限地基辐射阻尼、混凝土损伤开裂非线性和横缝接触非线性等关键影响因素,研究了大岗山拱坝的地震响应.何建涛等[9]综合考虑坝体混凝土和坝基岩体的材料非线性、无限地基辐射阻尼等因素,对Koyna重力坝进行了地震响应分析.王海波等[10]采用全坝段三维有限元模型、计入地基辐射阻尼以及坝段间动态接触这些因素,研究了其对混凝土重力坝地震响应的影响.
在大坝-库水动力相互作用分析方面,自Westergaard开创性研究以来,国内外研究者对于库水可压缩性、库底边界的吸收作用等方面的研究一直不断.林皋等[11]推导了综合考虑库水可压缩性和库底吸收边界的坝面动水压力方程,提出了一种求解坝面动水压力的半解析方法.王翔等[12]基于标量波动方程建立了求解混凝土坝动水压力波的高阶双渐近透射边界,发展了混凝土坝-库水动力相互作用时域分析的耦合模型.高毅超等[13]将高阶双渐近透射边界直接嵌入到近场有限元方程中,建立了大坝-库水动力相互作用的直接耦合分析模型.王俊等[14]通过对比流固耦合模型与附加质量模型的坝体损伤来分析结果,发现流固耦合模型分析大坝-水库系统相互作用更贴近实际情况.陈灯红等[15]研究了库水压缩性及分缝布置对高拱坝非线性地震响应的影响.刘明志等[16]探讨了库水可压缩性对重力坝动力特性和地震响应的影响.
在这些研究中,学者们建立了多种模型来模拟大坝-地基、大坝-库水及大坝-库水-地基耦合系统的动力相互作用,但在有限元数值分析中,对于基础与库水的模拟方法以及基础与库水截断边界的范围尚未达成一致,大多数情况据经验选取.本文将以黄登重力坝12号坝段为研究对象,考虑不同地基尺寸、地基辐射阻尼和库水可压缩性这些因素,分析大坝地震动力响应作用,并分别与无质量地基及附加质量模型的分析结果进行对比,以此来分析这些因素对混凝土重力坝地震响应的定量影响,为大坝抗震设计提供参考.
1 大坝-地基-库水系统模型建立
1.1 大坝-地基系统相互作用模型
在大坝-地基相互作用的研究中,工程上最常用的是无质量地基模型,即只截取结构周围一定范围内的地基,并假定地基是线弹性、无质量的.但实际上地基是有质量的半无限介质,若使用无质量地基模型则无法考虑远域地基的辐射阻尼效应.为了模拟远域地基的辐射阻尼效应,更加真实地反映坝体地震响应,需要在其边界处施加人为处理的边界条件.黏弹性边界是由Deeks、Randolph[17]在黏性边界基础上提出的,其基本思想是在截断边界上设置并联的弹簧-阻尼器物理元件,刘晶波等[18]基于球面波动方程将黏弹性边界推广应用到三维情况.黏弹性边界具有能同时模拟散射波辐射和半无限地基的弹性恢复能力的优点,且能克服黏性边界引起的低频漂移问题,稳定性好,并且物理意义明确,容易与有限元程序结合,因此在实际工程中得到了一些应用.
在黏弹性边界的施加过程中,对于人工边界上的弹簧、阻尼器的弹簧刚度和阻尼系数,不同学者给出了相应建议.本文二维黏弹性人工边界等效物理系统的法向与切向弹簧系数、阻尼系数[19]分别取为:
法向边界:

切向边界:

式中:KBT、KBN分别为弹簧切向与法向刚度系数;R为近场结构几何中心至人工边界点的距离;cs、cp分别为SV 波和P波波速;G 为介质剪切模量;ρ为介质密度;αN、αT分别为黏弹性人工边界的法向、切向参数,本文αN取为1.0,αT取为0.5.
在施加二维人工边界的弹簧-阻尼器元件时,只需将式(1)和(2)中的系数乘以边界上结点影响面积施加在截断边界结点上即可,其二维示意图如图1所示.
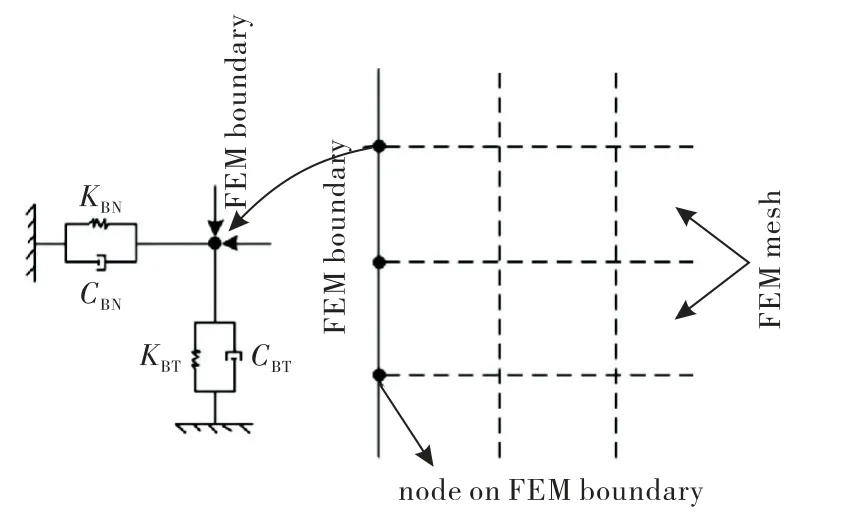
图1 二维黏弹性边界物理意义示意图
对于黏弹性人工边界上的波动输入问题,采用将波动散射问题转化为波源问题的方法来实现,即通过在人工边界节点上施加等效荷载来实现,施加在黏弹性边界节点的切向与法向等效荷载[19]可表示为:
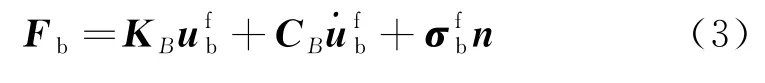
式中:n为人工边界外法线方向余弦向量;K B和C B分别为以黏弹性人工边界弹簧系数、阻尼系数为元素的对角矩阵分别为自由场位移、速度和应力矢量.
1.2 大坝-库水相互作用模型
水体对坝体的作用可以分为两种,一是静水压力,二是地震作用下的惯性力,大坝在地震荷载的持续作用下,水体会随着大坝不断地做往复运动,反之水体产生的惯性力又反作用于坝体上,即为动水压力.在水体对坝体表面产生的动水压力的研究中,常有两种计算方法:
1)附加质量法
该方法由Westergaard于1933 年提出,假定坝面是直立刚性的,库水上游方向无穷远,库底为刚性水平面.该方法可忽略库水的可压缩性以及坝体的变形因素,其表达式为:
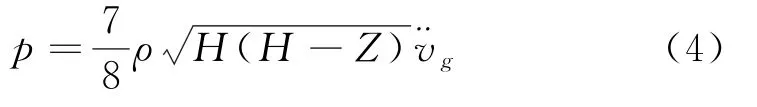
式中:p为坝面某点受到的动水压力;ρ为库水质量密度;H为坝前库水深度;Z为该点在坝基面以上的高 度为坝面结点加速度.
2)流固耦合法
该方法首先将水体假设为均匀、可压缩的、无旋度无黏性的理想流体,基于这种假定,可以得到以压力p为未知量的波动方程[20]:

其中:▽为拉普拉斯算子;p为动水压力;c为压声波波速;K为流体体积模量;ρ为流体密度.
在设定边界条件后,考虑结构位移和流体速度势组成的混合未知量的有限元方程[20]为:
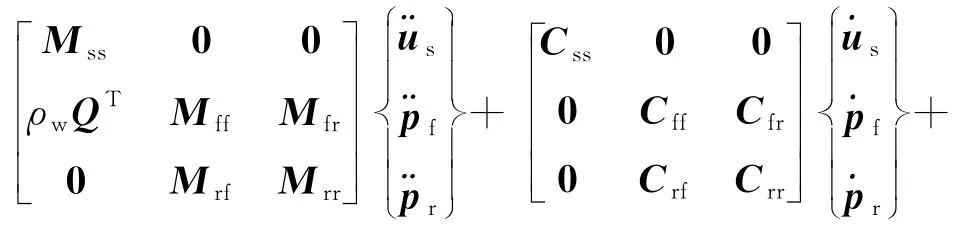
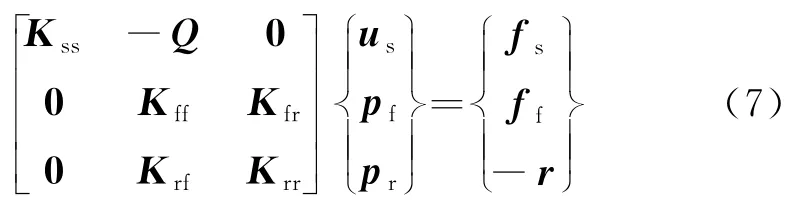
式中:M、C、K分别为质量矩阵、阻尼矩阵和刚度矩阵;Q为流固交界面上的耦合矩阵;u和p分别为位移和动水压力;f为外力矢量;r为近场水作用于水库的相互作用力矢量.下标s为坝体上的自由度;下标f表示近场水域的自由度;下标r表示截断边界上的自由度.
2 算例验证
以国际大坝委员会发布的第十五届大坝数值分析基准算例研讨会主题A 中的Pine Flat重力坝地震响应分析为例[21],验证构建的重力坝-地基-库水系统地震响应分析模型的正确性.混凝土与地基的弹性模量E=22.41 GPa,泊松比ν=0.2,密度ρ=2 483 kg/m3;水体体积模量K=2.07 GPa,密度ρw=1 000 kg/m3.采用基于有限元法的黏弹性边界模拟无限坝基,采用等效荷载法实现地震动输入,采用声学单元及无反射边界条件模拟坝-库动力相互作用[20].有限元网格采用四结点四边形平面应变单元离散,共划分了6 417个单元6 720个结点,计算网格如图2所示,输入的Taft地震波如图3所示.
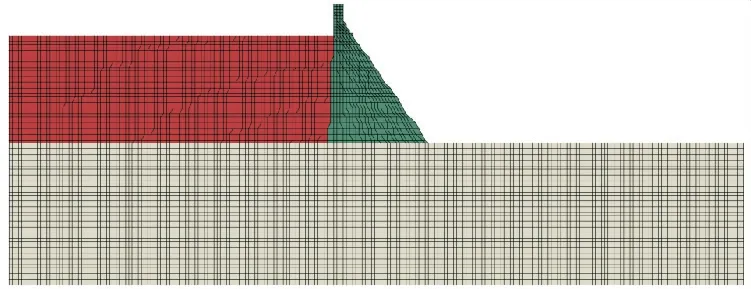
图2 Pine Flat重力坝-地基-库水系统有限元网格图
为了说明构建耦合模型的优越性,采用文献[21]中基于比例边界有限元法的计算模型结果进行了对比,其中采用声学单元及基于标量波波动方程的高阶双渐近透射边界模拟坝-库动力相互作用,采用位移单位脉冲响应函数算法及相适配的地震动输入方法模拟坝-基动力相互作用.坝顶水平向位移、加速度结果及相对水平位移结果的比较如图4~6所示,结果表明本文构建的耦合模型结果与基于比例边界有限元法模型的结果[21]相比具有良好的计算精度和效率.

图5 坝顶水平加速度结果的比较

图6 相对水平位移结果的比较
3 工程应用
3.1 工程概况
黄登水电站位于云南省兰坪县境内,上游与托巴水电站,下游与大华桥水电站相衔接.坝址控制流域面积9.19×104km2,总库容约为1.5×109m3,多年平均流量901 m3/s.黄登水利工程为混凝土重力坝,最大坝高203 m,属Ⅰ等大(1)型工程.本次模拟选用12号挡水坝段进行数值模拟计算,坝顶高程1625m,坝基面高程1422 m,坝高203 m,坝顶宽16 m,正常蓄水位1 619 m,如图7所示.

图7 12号挡水坝段断面(单位:m)
计算内容共分为A、B、C 3种工况,分别考虑地基尺寸大小、地基辐射阻尼以及库水可压缩性等各项影响因素探究其对重力坝动力响应的影响.并分别以A、B、C表示这3种工况,各工况汇总见表1.其中H表示大坝高度,L1表示地基范围从坝踵往上游方向延伸尺寸,L2表示从坝趾往下游方向延伸尺寸,H0表示地基深度,L表示库水长度.

表1 计算工况汇总表
3.2 计算模型
计算采用平面有限元分析方法,基于Abaqus有限元仿真软件实现.计算中考虑了坝体自重及以正常蓄水位下的静水压力等荷载,地震荷载选用Koyna地震动.坝体采用平面应力单元,地基采用平面应变单元,网格尺寸均为2 m×2 m.当动水压力以Westergaard公式计算的附加质量模拟,施加在坝体的上游迎水面时,建立有限元模型如图8所示;当库水动水压力采用声学单元模拟,施加在坝体的上游迎水面时,其有限元模型如图9所示.工况A 和工况C 采用无质量地基模型,边界条件为:对侧边界施加法向约束,底部边界全部约束;工况B采用有质量地基模型,截断人工边界采用黏弹性边界来模拟无限地基的辐射阻尼效应,其中,在Abaqus进行结构整体静动力分析中,通过一种单元“生死”技术[22],实现静态约束边界到动态黏弹性边界的稳定切换,从而实现静动力统一计算.

图8 工况C1计算模型

图9 工况C2计算模型
3.3 模型参数
坝体不模拟分区,只采用一种混凝土材料,并假定为线弹性,动弹模取为静弹模的1.5倍[23];地基岩体假定为均质线弹性介质,且忽略材料阻尼.具体材料参数见表2.
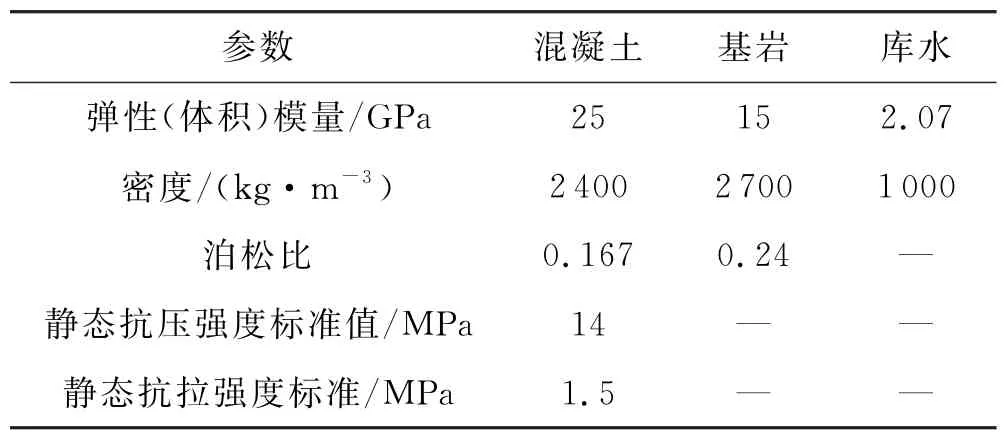
表2 材料参数
此外,在实际的动态分析中还需考虑混凝土的阻尼,本文采用瑞利阻尼的标准形式来计算,即两参数计算模型如下:

其中:ω1、ω2分别为系统的前两阶自振频率;ξ为阻尼系数,本文取ξ=5%[24].
3.4 计算荷载
本工况中选取黄登混凝土重力坝12 号挡水坝段,考虑上游正常蓄水位情况进行数值模拟计算,作用荷载包括自重、静水压力、动水压力和地震荷载.
地震荷载的计算采用了Koyna地震时程,地震总历时为10 s,选择固定时间步长Δt=0.01 s进行计算.水平和垂直加速度时程如图10所示.

图10 输入的地震加速度时程
4 地基尺寸的敏感度分析
工况A 为探究地基尺寸对重力坝动力响应的影响,地基范围为从坝踵往上游方向、从坝趾往下游方向、坝基往深度方向均分别延伸1.5倍、2倍、3倍坝高,并分别以A1、A2、A3表示这3种工况.动水压力以Westergaard 公式计算的动水附加质量模拟,施加在坝体的上游迎水面.
4.1 位移分析
上述模型的坝顶、坝踵的水平加速度峰值、水平位移峰值汇总见表3,坝踵点与坝顶点的水平相对位移时程如图11所示.

表3 工况A坝顶、坝踵水平加速度与位移峰值
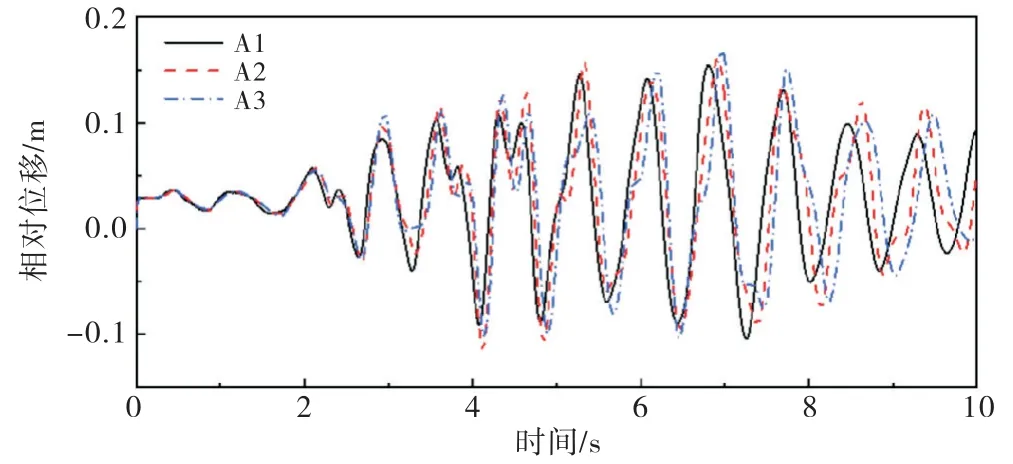
图11 工况A 相对水平位移时程曲线
由表3可以看出,地基尺寸对大坝加速度响应有显著影响,坝顶加速度在2 倍坝高时达到最大,为26.53 m/s2,而地基尺寸对位移影响较小,当地基范围分别延伸1.5倍、2倍、3倍坝高时,坝踵点与坝顶点的水平相对位移峰值呈现递增规律,3倍坝高时水平相对位移峰值较1.5倍坝高增加了8.7%.
4.2 应力分析
选取坝体坝踵和坝趾部位作为特征点,各工况下的主拉应力和主压应力结果如图12~13所示.各工况的最大主拉应力均发生在坝踵处,拉应力峰值分别为14.79、13.48、10.31 MPa;最大主压应力发生在坝趾处,压应力峰值分别为-31.23、-29.15、-28.71 MPa.由此可见,在一定范围内,随着地基尺寸的增大,坝体的主拉应力、主压应力峰值均呈现递减趋势,地基尺寸为3倍坝高的最大拉应力峰值较1.5倍坝高减小了30.3%.
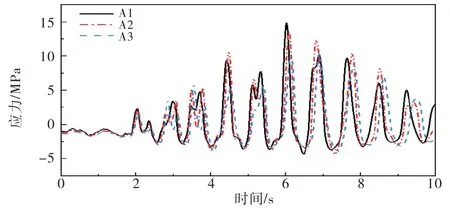
图12 工况A 坝踵主拉应力时程曲线
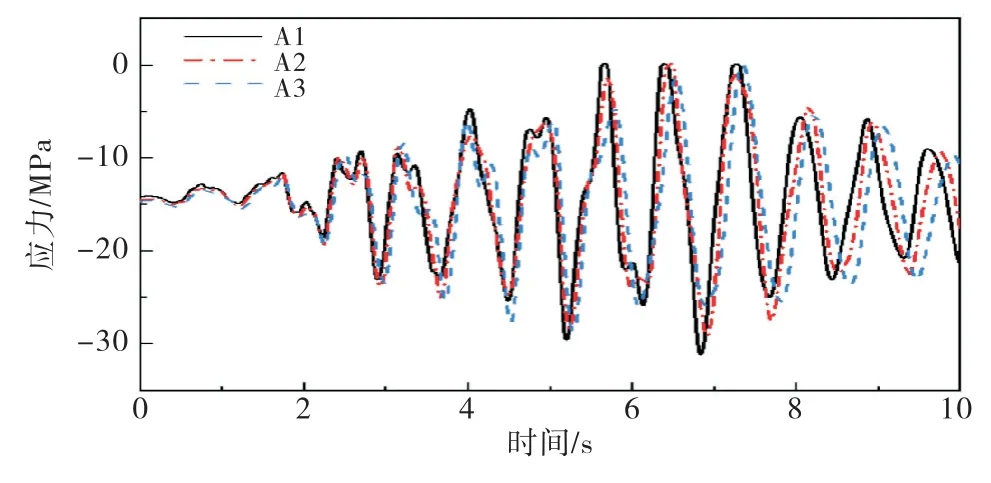
图13 工况A 坝趾主压应力时程曲线
5 地基辐射阻尼对重力坝地震响应的影响
在考虑地基质量的情况下,本节探究地基辐射阻尼对重力坝动力响应的影响,截断地基人工边界选用黏弹性人工边界,动水压力采用附加质量模型,采用和工况A 相同的地基尺寸,即从坝踵往上游方向、从坝趾往下游方向、坝基往深度方向均分别延伸1.5倍、2倍、3倍坝高,并分别以工况B1、B2、B3表示.
5.1 位移分析
坝顶、坝踵的水平加速度、水平位移峰值汇总见表4,坝踵点与坝顶点的相对位移时程如图14所示.
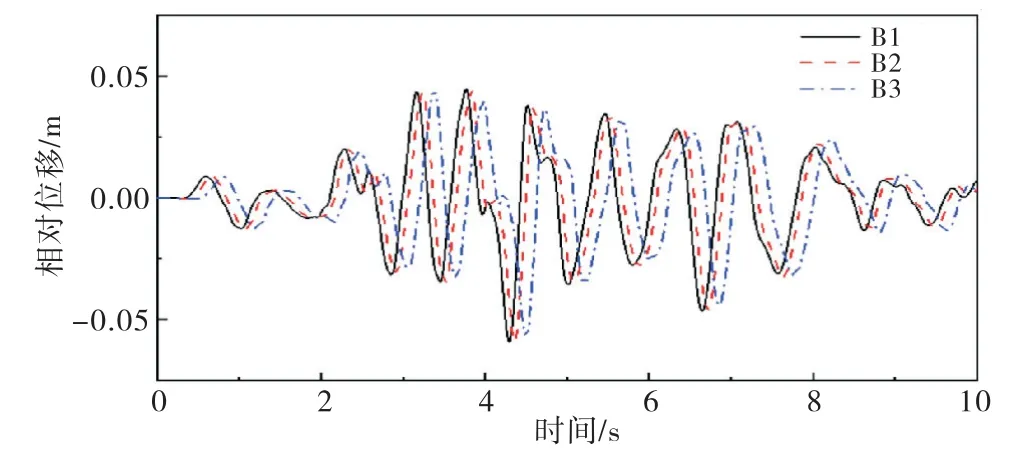
图14 工况B相对水平位移时程曲线

表4 工况B坝顶、坝踵水平加速度与位移峰值
对比表4与表3可以看出,黏弹性边界模型考虑了地基的辐射阻尼效应后较无质量地基模型,坝顶或坝踵的加速度峰值降低了6%~63%,坝踵及坝顶水平位移峰值降低了60%左右,相对位移峰值降低了50%左右;并且,随着地基尺寸的增加,坝踵及坝顶点相对位移峰值呈现上升趋势.由此可见,无质量地基模型夸大了坝体的地震响应,考虑地基辐射阻尼对大坝进行动力响应分析有着重要的影响.
5.2 应力分析
各工况下的主拉应力和主压应力结果如图15~16所示.当地基范围分别延伸1.5倍、2倍、3倍坝高时,坝踵的主拉应力峰值分别为6.33、5.63、4.97 MPa;坝趾的主压应力峰值分别为-18.9、-19.29、-19.37 MPa,在一定范围内,随着地基尺寸的增大,拉应力峰值则呈递减趋势.同时,与无质量地基模型的结果比较,考虑黏弹性边界的坝体主拉、压应力峰值也出现不同程度的减小.最大主拉应力发生在坝踵点,最大主压应力发生在坝趾,与无质量地基模型的结果相比,主拉应力峰值降低了50%~60%,主压应力峰值降低了30%~40%.
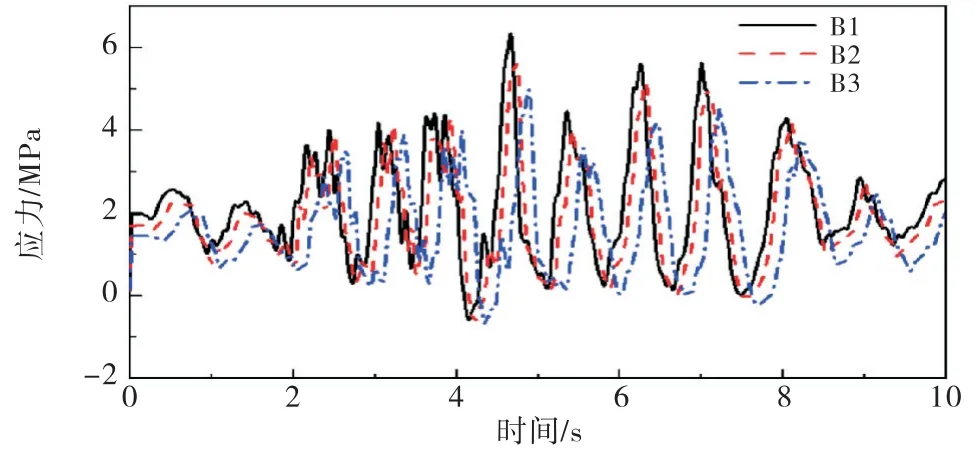
图15 工况B坝踵主拉应力时程曲线
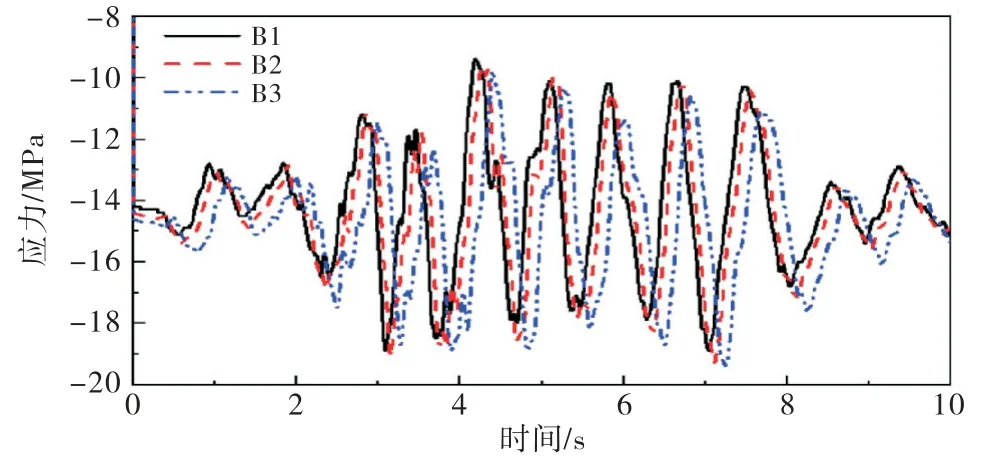
图16 工况B坝趾主压应力时程曲线
6 库水压缩性对重力坝地震响应的影响
本节分析库水的压缩性对重力坝动力响应的影响.不可压缩性库水采用Westergaard 附加质量模型;可压缩库水可用有限元模拟,在库水面上采用自由表面边界条件,在库水远端采用无反射边界条件,在库水-大坝、库水-地基交界处采用流固耦合边界条件[20].
工况C采用无质量地基模型,地基尺寸从坝趾往下游、深度均延伸1.0倍坝高,从坝踵往上游分别延伸3、4、5倍坝高.在工况C1中,动水压力以Westergaard 公式计算的附加质量单元模拟;工况C2、C3、C4中,动水压力采用声学单元模拟.
6.1 位移分析
表5为4种工况下的坝体动力响应极值汇总,图17为坝踵与坝顶点相对位移时程曲线.对于相同地基尺寸而言,可压缩库水模型较Westergaard附加质量模型的水平相对位移降低了13.8%;当库水长度分别为3、4及5倍坝高时,水平相对位移峰值呈现上升趋势.

表5 工况C坝顶、坝踵的水平加速度与位移峰值

图17 工况C相对水平位移时程曲线
6.2 应力分析
选取坝体坝踵和坝趾部位作为特征点,不同工况下得到的坝体-库水界面的主拉应力和主压应力结果如图18~19 所示.C 工况中主拉应力峰值分别为15.26、9.32、9.68、10.28 MPa;主压应力峰值分别为-32.80、-23.25、-24.41、-25.50 MPa.由此可见,与附加质量模型结果相比,流固耦合模型的主拉应力以及主压应力的峰值均有所降低,降幅在30%左右;当库水长度分别为3、4及5倍坝高时,主拉应力峰值呈现递增趋势.
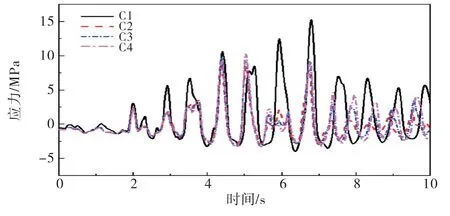
图18 工况C坝踵主拉应力时程曲线

图19 工况C坝趾主压应力时程曲线
7 结论
本文基于构建的重力坝-地基-库水系统模型以黄登混凝土重力坝12 号坝段为研究对象,分别以A~C 10种工况探究了地基尺寸、无限地基辐射阻尼效应及库水可压缩性这些重要因素影响的重力坝-地基-库水系统地震响应.得出主要结论如下:
1)地基尺寸对大坝加速度响应有显著影响,对位移影响较小,坝顶加速度在2倍坝高时达到最大,为26.53 m/s2,当地基范围分别延伸1.5、2、3 倍坝高时,坝踵与坝顶的水平相对位移峰值呈现递增规律,地基尺寸为3倍坝高时水平相对位移峰值较1.5倍坝高增加了8.7%,坝体的最大拉应力峰值呈现递减趋势,地基尺寸为3倍坝高的最大拉应力峰值较1.5倍坝高降低了30.3%.
2)黏弹性边界模型考虑了地基的辐射阻尼效应后较之无质量地基模型,动力响应均有不同程度的降低,坝顶和坝踵的加速度峰值降低了6%~63%,位移峰值降低了60%左右,相对位移峰值降低了50%左右.同时,坝体主拉、压应力峰值也出现不同程度的减小,拉应力峰值降低了50%~60%,压应力峰值降低了30%~40%.由此可见,坝体与地基的动力相互作用不容忽视,应考虑辐射阻尼效应,黏弹性人工边界模型比无质量地基模型更能有效地模拟远场地基的辐射阻尼效应.
3)对比流固耦合模型与Westergaard附加质量模型发现,附加质量模型会夸大动水压力作用.当地基尺寸相同时,流固耦合模型较附加质量模型的水平相对位移降低13.8%,坝体应力峰值降低30%左右.因此,对比流固耦合模型比较与传统Westergaard附加质量模型,前者模拟坝体-库水之间的相互作用更为合理.
