地理视角下深圳市房价及其影响因素研究——基于随机森林模型

钟艾妮，答星，喻静敏

(武汉市测绘研究院，湖北 武汉 430022)

1 引 言

随着我国经济发展和人民生活质量的稳步提升，城市房价成为社会关切的重要问题。房价是多因素作用下的高度复杂问题，其变化规律具有非线性、动态性和偶然性[1]。关于住房的调查研究显示，房价不仅受经济、政策的影响，还和房屋地理区位、房屋配套设施、人的行为、城市规划等诸多因素有关。从空间视角探索城市房价特征和影响因素，是地理空间分析的重要研究范畴。

传统的房价研究着重于分析房屋销售价格的特征和趋势，相关方法主要来源于经济学与统计学，包括灰色理论[2]、传统的时间序列法[3]等。以往的文献研究是研究区域的经济发展指标和住宅本身的建筑属性等进行房价预测和影响因素分析，大多是基于前期累积的房价统计结果进行推演[4～7]。而我国区域房价格通常呈现出空间分异特征，城市内部房屋销售价格也频繁出现起伏，传统的研究方法在小尺度的房价分析上不具有适用性。

从当前的房屋市场交易情况来看，城镇居民在选择住房时，已经不单单是考虑房屋自身的内部结构等建筑属性，更多的关注与房屋地理空间位置相关的交通、公共服务、未来规划等配置属性。这些空间配置属性对居民生活品质的提升有极大影响，与房价存在关联关系[8，9]，近年来学者们开始关注住宅的空间属性，探究房价的地理影响因素。方晓萍等人根据全国35个大中城市房价波动发现其具有地理扩散特征[10]；顾衡宇等人基于改进的空间句法研究路网形态对房价的影响[11]；杨兵分析了大连市二手房价格的空间相关性及聚集特征[12]。GIS领域研究者大多利用多元线性回归、地理加权回归等模型探索地理环境对房价影响的空间差异并实现房价预测[13～15]，但这类方法进行回归分析会存在多重共线性，不能较好分析预测房价。与全局线性和多项式回归模型相比，随机森林模型是多个决策树的集成，借助决策树算法，可以将输入空间分割为更小的区域，使结果可管可控，更适用于动态非线性特征的房价预测和分析。

借助随机森林模型，本文以深圳市二手房房价为研究对象，充分考虑房屋住宅的地理空间属性，参考已有研究[16，17]，选取教育资源、医疗设施、交通便捷度、环境因素、规划因素方面的7个指标作为房价影响因子。通过研究深圳市房价的空间分布特征及规律，分析小尺度上居民对房屋不同地理环境因素的关注度差异，从地理视角下推测房价，以期辅助城市住宅规划建设，为相关部门提供参考以便科学制定相应方针政策。

2 基于随机森林模型的房价研究

作为新兴起的、高度灵活的一种机器学习算法，随机森林(Random Forest)是由Leo Breiman提出的一种机器学习算法[18]，其本质属于集成学习，具有学习速度快、分类准确度高、泛化误差小、参数敏感度低、计算开销少等特点。随机森林模型主要用于回归和分类，在估计推断映射方面有准确率优势，目前已被广泛应用到众多领域，如生物信息、金融经济、新能源、化工产业等，都取得了非常好的效果[19]。

2.1 随机森林相关知识

随机森林模型的基本单元是决策树。决策树是通过构造一种树形结构来进行问题决策，是直观运用概率分析的一种图解法，每个内部节点表示某种特征的测试，每个分支代表一个测试输出，每个叶节点是输出结果。

决策树中进行特征选取的依据和条件是熵值下降最快，提高数据集的纯度。CART树通过基尼(Gini)指数计算每个变量对决策树每个节点上观测值的异质性的影响，该指数值越小纯度越高。若选取的属性为A，那么分裂后的数据集D的基尼指数的计算公式为：

(1)

2.2 房价研究的随机森林模型原理

由于单决策树分类或回归结果可能不稳定，随机森林的基本思想则是将许多决策树集成为一个强组合。通过多个相互独立的决策树之间的互补作用，随机性选择训练集并随机选取特征，以随机森林模型进行房价分析预测，避免了过拟合问题且能一定程度上纠正局部过拟合，相较以往研究使用的方法，具有很好的泛化性能、鲁棒性和模型稳定性[20]。

本文采用的随机森林模型是由分类回归树(classification and regression trees，CART)(基决策树)集合{h(X，βk)，k=1，2，…，i}组成的集成器。以Gini指数作为指标来分裂属性，h(X，βk)表示第k棵基决策树，βk表示第k棵基决策树的随机向量，X是独立分布的随机向量，i表示随机森林中基决策树的个数。对于输入向量X的分类结果，随机森林模型基于每棵基决策树的判断投票结果做出最终输出决策。

图1 随机森林模型原理

算法流程如下：

(1)以样本房价作为训练集，随机分成k个训练样本分别训练房价决策树，选取的房价地理环境影响因素作为特征，输入特征构成的多维向量；

(2)在每棵决策树的节点随机选取特征进行Gini指标计算，不断划分，得到最终的所有决策树；

(3)本文使用随机森林模型进行回归分析，预测值取所有树预测值的平均。

3 研究区域与数据源

本文选取的研究区域为深圳市，深圳市作为一线城市，社会经济发展迅速，建设用地资源紧缺，房价存在明显空间差异。

研究的数据源包括深圳市房价数据和电子地图数据。①房价数据。深圳市二手房住宅交易活跃，是市场交易的主流，因此本文以住宅小区二手房交易价格为研究对象，通过爬虫技术从深圳市二手房交易网站获取住宅小区地址坐标并计算2019年各小区单价平均值，共 1 225条记录。②深圳市电子地图数据。深圳市基础设施及相关空间数据，包括深圳市小学、中学、医院、轨道站点的POI数据，路网数据，及公园绿地、重点规划区面状数据。

本文以居民享受的生活服务及基础设施为切入点，考虑环境和规划因素，选取深圳市各小区的7个地理空间因子作为影响房价的指标，以住宅小区一公里范围缓冲区为基础研究单元，具体信息如表1所示。

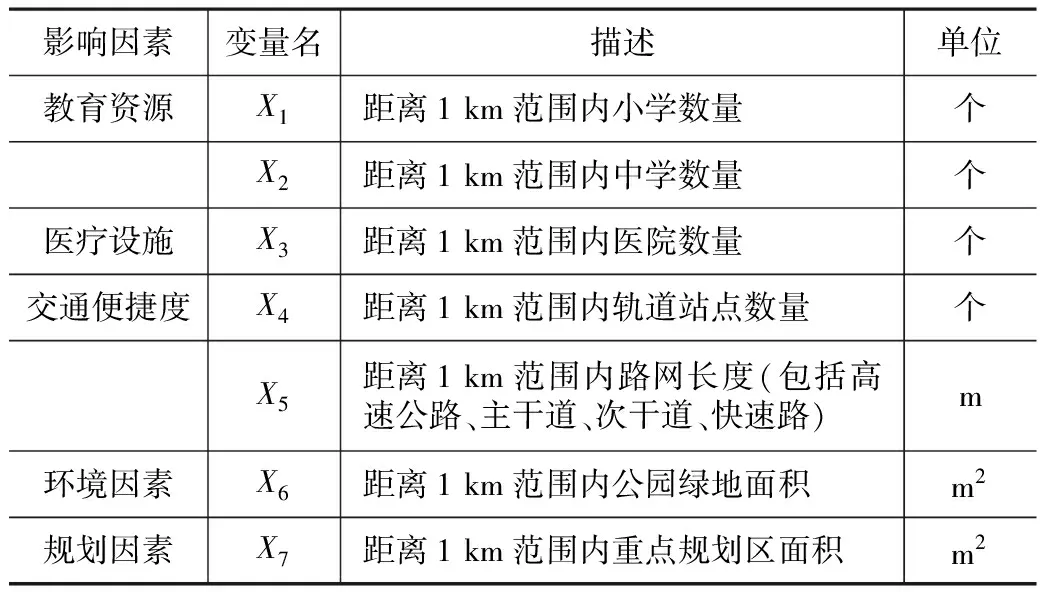
影响房价的地理空间因素及指标 表1

4 实验设计与结果分析

4.1 深圳市房价空间分异特征

根据安居客网站公开的深圳市房价数据可知，各区县存在显著差异，南山区均价最高，坪山区最低。通过对爬取的 1 225条房价实验数据及公开的均价统计数据进行可视化(如图2所示)，结果显示二手房均价较高的住宅小区集中在南山区和福田区，且交易量也较多。深圳市房价在整体上呈现出南高北低、西高东低的特征，以南山区和福田区为中心向外逐渐减低。从空间视角看，这与深圳市公共服务设施的分布特征呈现出相似性。

图2 深圳市房价空间分异特征

4.2 房价研究随机森林模型建立

通过整理所有1 225条房价及其影响因素数据，随机选取共925条数据作为随机森林模型的训练样本，以7个影响因素指标作为自变量，住宅小区均价作为因变量，利用OpenCV2的随机森林模型工具进行回归分析。用剩余的300条数据作为测试数据进行后续预测分析。深圳市房价随机森林模型的训练参数如表2所示。

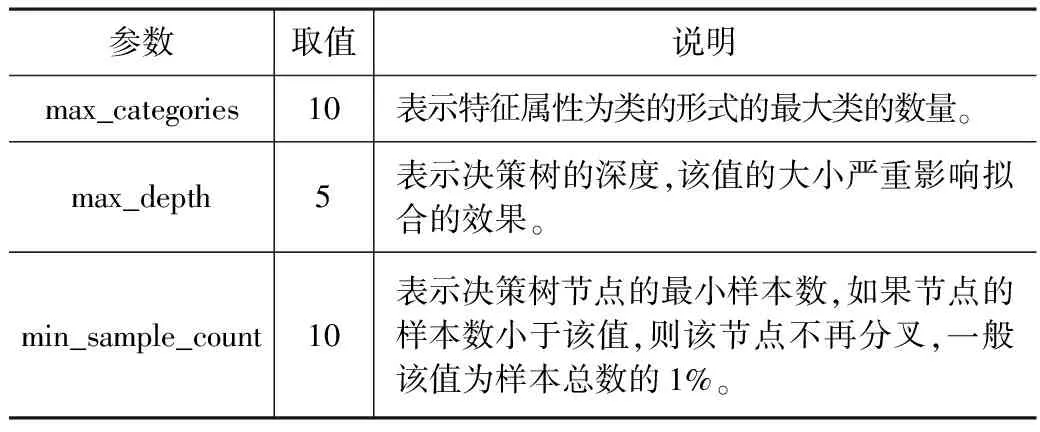
随机森林模型训练参数 表2

根据本文选取的房价影响指标，预选的特征变量个数为7，设置最大分类数为10，由于特征数量相对较少，决策树的最大分类深度设为5，节点最小样本数为10，其余均选择默认值，训练完成后随机森林中生成了50颗决策树。对所有的输入特征变量进行分析，计算决策树中每个节点处的Gini指数反映不纯度转化值，取均值即获取每一个自变量对因变量的解释程度，用来评价各特征变量的相对重要性。

4.3 影响因素重要性分析

根据建立的房价研究随机森林模型的输出数据进行计算，结果如表3所示，Gini指数的取值越小，代表自变量对因变量的影响越大。

对各特征变量Gini指数进行标准化处理，通过直方图反映相对重要性，如图3所示，7个指标因子在房价模型中的重要性排序如下：X3>X2>X7>X6>X1>X5>X4。该结果反映出深圳市的二手住宅小区单价在选取的以上7个指标因子中，受到医疗设施因素的影响最甚，小区附近的医疗资源越充分，房价越高，这和深圳市医疗资源分布的不均衡有很大关系。其次小区附近的中学分布数量也是影响房价的一个重要因素，仅次于医院，教育资源配置对房价有提升作用。重点规划区因素是重要性排在第三位的因素，反映深圳市的房价越昂贵的小区，往往是位于深圳市重点规划区的附近，政府的规划决策等对城市的房价有着重要的影响。公园绿地的分布面积影响次之，然后是小学的分布数量，交通便捷方面的影响因素对小区单价的影响最低。

各个特征变量在模型中的Gini指数 表3

图3 变量相对重要性

4.4 预测分析

利用生成的深圳房价随机森林预测模型对300条测试数据进行运算，根据各影响因子的指标值得出了预测房价。通过对预测结果和实际房价数据建立折线图进行可视化表达，结果如图4所示。在整体上预测结果能够大致吻合测试数据中的实际房价，但随机森林生成的预测结果在各个极大值处均小于实际房价值，各个极小值处均高于实际房价，即预测结果偏向于均值上下浮动，不如实际房价值的差异那么显著。针对价格相对稳定在深圳市房价均值上下的住宅小区，本文使用的模型能够较好地实现价格预测；对于较高的住宅小区单价，随机森林模型的预测结果会存在较大偏差，仅利用地理视角的因素不能较好推测该类房价，存在其他主要影响因素。

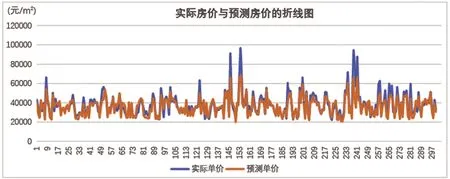
图4 预测结果与实际价格对比折线图

预测房价和实际房价的统计特征计算结果如表4所示，预测房价的均值与实际房价的均值大致相同；然而实际房价的标准差远大于预测房价，标准差是用来衡量一组数自身的离散程度的指标，因此说明实际房价数据较为离散，数据间偏差大于预测房价，预测房价值相对趋于均值；预测房价的最大值低于实际房价最高值约2万元，而对于最小值的情况，预测房价的最小值要高于实际房价。结合图4和表4中结果，显示出模型对于处于高值和低值的房价难以进行很好的模拟，但对于位于均值附近的房价能够实现较好的预测，相对误差较小。

预测房价和实际房价的统计特征 表4

(2)

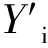
图5 实际价格与预测误差散点图

5 结 论

本文通过网络爬取深圳市二手房住宅小区均价 1 225条，以小区一公里范围内的医疗设施、教育资源、交通便捷度、环境、规划的享有程度，从地理视角下选取小学、中学共7个指标，通过机器学习中的随机森林建立研究模型，分析深圳市房价的地理空间影响因素。

根据本文建立的深圳市房价研究随机森林模型，对所选7个地理空间变量的回归分析，通过输出的变量重要性评价指标反映各个特征变量对深圳市二手房住宅小区均价的影响程度，结果显示医院分布特征是对房价影响最大的因子，反映出深圳市医疗设施的不充分和不均衡，在今后的城市规划中需重点考虑布局；其次是中学的分布，教育资源配置是居民选购房屋时会着重考虑的因素，对住宅小区的价格有重要影响；重点规划区因素是重要性排在第三位的因素，政府的规划决策等对城市的房价有着重要的影响，周边区域的发展状况影响居住区销售价格；公园绿地面积排在第四位，居民享有的公共绿色开敞空间也对房价有一定影响；再次是小学分布数量特征，反映交通便捷度的路网、轨道站点在房价影响上相对重要性最低。通过对测试数据进行房价预测，本文提出的方法在住宅小区单价处于均值附近的情况下，能够较好吻合实际房价统计数据，地理环境影响因子对该类房价具有较好的解释和预测效果。