一种基于深度融合模型的滚动轴承故障诊断方法

刘 伟 单雪垠 李双喜* 王 旭 姚思雨

(1.北京化工大学 机电工程学院，北京 100029；2.石河子大学 机械电气工程学院，石河子 832003)

引 言

滚动轴承是旋转机械设备的核心部件之一[1-2]，其健康状况会直接影响设备的可靠性和稳定性，研究表明大约45%～55%的机械设备事故与滚动轴承有关[3]，因此针对轴承的设备故障诊断在工业界具有重要的应用价值[4-5]。

传统的故障诊断方法通常以振动信号分析为基础[6-7]，通过包络谱提取故障特征频率来实现轴承状态监测。然而，该方法在一定程度上依赖于复杂的信号处理方法和丰富的专家经验，难以实现设备故障的自动诊断。近年来，随着人工智能和深度学习技术的深入发展，数据驱动的智能故障诊断方法得到广泛关注[8]。2006年，Hinton等[9]首次提出深度信念网络(deep belief network，DBN)，由于其具有自主提取特征和表达复杂非线性关系的优点，已经被广泛应用于语音识别和目标检测领域。在机械故障诊断领域，Tamilselvan等[10]开发了一种基于DBN的多传感器状态监测算法，并首次应用于飞机发动机的故障诊断。赵光权等[11]利用DBN在特征提取和处理高维非线性数据方面的优势，提出一种基于DBN的故障特征提取及诊断方法。刘秀丽等[12]将DBN应用于风电机组行星齿轮箱的故障诊断，通过微调DBN得到了精度更高的故障诊断结果。陈建业等[13]首先使用等距映射算法将信号的特征数据映射到低维空间，然后融合DBN来诊断齿轮的故障状态。张朝龙等[14]将混沌粒子群优化算法和DBN结合提取模拟电路的早期故障特征。随后，李俊卿等[15]以受限玻尔兹曼机为基本单元搭建DBN，并用于同步发电机的故障诊断。魏乐等[16]针对传统受限玻尔兹曼机输入向量受限于伯努利二值分布且对于非二项分布的数据重构拟合效果较差的问题，引入高斯-伯努利受限玻尔兹曼机模型用于旋转机械的故障诊断。苏磊等[17]提出一种基于DBN的变压器运行状态分析方法。

然而，以上研究没有考虑到复杂工况下环境噪声对DBN产生的影响。在实际生产过程中，机械设备的运行工况和工作环境复杂多变，传感器采集到的振动信号不可避免受到多种噪声的影响[18]，这些噪声将有效信号淹没，导致难以提取信号的特征，严重影响了深度信念网络的故障识别精度。为此，本文提出一种基于DBN的深度融合模型，引入卷积降噪自编码器(convolutional denoising autoencoder，CDAE)，在提取信号特征的同时进行降噪。提出的融合模型将CDAE与DBN相结合，前者侧重提取振动信号的浅层特征，后者则着重提取深层特征，随后通过Adam算法对网络训练过程进行优化。实验结果表明所提融合模型具有更强的特征学习能力和抗干扰能力，且极大提高了网络的诊断精度。

1 深度学习方法

1.1 深度信念网络

DBN由一系列受限玻尔兹曼机(restricted Botlzmann machine，RBM)堆叠而成[19]。RBM采用双层结构(图1)，上层为隐藏层(H)，下层为可见层(V)，隐藏层与可见层之间为全连接，各个隐藏层之间和各个可见层之间都是独立的。可见层用来接收输入信号，隐藏层用来提取特征，通过求解网络的能量函数可以得到输入样本的分布。值得注意的是，这是一个包含可见层向量和隐藏层向量以及权重和偏移量的函数，对这个函数求对数似然，便可得出各层之间的权重和偏移量。RBM的训练过程实际上是计算一个最能产生训练样本的概率分布，也就是说，要求得一个分布，在这个分布里，训练样本的概率最大。

图1 受限玻尔兹曼机结构

一般的DBN训练步骤如下：(1)充分训练第一个RBM；(2)固定第一个RBM的权重和偏移量，然后使用其隐性神经元的状态作为第二个RBM的输入向量，充分训练第二个RBM；(3)将第二个RBM堆叠在第一个RBM的上方；(4)重复上述3个步骤任意多次。

由于机械设备的工作环境恶劣，当传感器采集到的振动信号受到噪声干扰时，DBN的故障诊断效果将大大降低，从而给工业生产带来较大的损失。为此，本文引入CDAE网络，提出一种基于CDAE和DBN的深度融合模型，在提取信号特征的同时进行降噪，以提高设备的故障诊断精度。

1.2 基于CDAE与DBN的融合模型

CDAE是传统自编码器(autoencoder，AE)的改进，它在AE重构信号的过程中加入有损失的信号，并将AE中的全连接层替换为卷积层。卷积层具有平移不变特性且能够学习对象的局部模型，这使得卷积层可以更有效地提取信号的特征。因此，CDAE具有比AE更强的鲁棒性。

图2所示为本文构建的CDAE模型，该模型由编码和解码两个过程组成。编码器输入的是随机有损的信号，经过卷积层与池化层降维得到隐藏层，编码部分的卷积核为3×3。池化层一般紧跟卷积层，它可以降低数据的维度从而加快网络的训练速度，这个降维的过程即为编码。编码将信号的有效信息紧缩在一个潜在空间中。数据从隐藏层到输出层是一个增维的解码过程，解码部分卷积核的大小也是3×3。在卷积层后放置反向池化层，反向池化层的作用与池化层相反，可以使数据层增加维度，通过多组卷积层与池化层将隐藏层的数据维度恢复到输入数据的维度，这个恢复数据维度的过程即为解码。编码-解码过程通过学习输入数据的模式与特征来重构原始信号，并补充信号中的有损部分最终达到降低干扰的目的。

图2 CDAE模型

为了提高轴承故障的诊断精度，增强网络的抗干扰能力，联合CDAE和DBN提出一种深度融合模型。该模型使用CDAE提取振动信号的浅层特征，在此基础之上基于DBN提取深层特征，最后利用softmax分类器根据深层特征分类得到故障诊断结果，其流程图如图3所示。

图3 融合模型流程图

传统DBN一般是由3个RBM与1个全连接层堆叠而成，而融合模型是将DBN的第一层RBM替换为CDAE。所提的CDAE-DBN融合模型结构如图4所示。输入数据首先通过CDAE层降噪，目的是获取更容易提取特征的信号数据，然后分别经过两个RBM层以提取特征，最后通过一个BP层得到输出数据。该模型可有效解决轴承输入信号中存在的因噪声干扰而影响故障诊断结果的问题。

图4 融合网络模型

基于融合模型实现轴承故障诊断的具体步骤如下：

1)使用传感器采集滚动轴承在不同工作状况下的振动数据；

2)按照2∶1的比例将数据等段均分并归一化处理，再将其划分为训练集和测试集；

3)使用CDAE模型处理测试集数据，提取轴承故障的浅层特征信息；

4)在步骤3)的基础上，使用DBN模型进一步提取轴承故障的深层特征信息；

5)使用softmax分类器对得到的深层轴承故障特征信息分类；

6)将测试集输入网络并按照步骤1)～5)处理得到测试集的训练结果，以此检验该网络的有效性。

2 滚动轴承故障诊断仿真分析

本文使用凯斯西储大学(Case Western Reserve University，CWRU)轴承数据集来验证所提CDAE-DBN融合模型的机械故障特征提取及诊断能力。

2.1 仿真信号

轴承实验台如图5所示，由一个1.47×103W的电动机、传感器、功率测试器和电子控制器组成。实验检测的轴承分别是支撑电动机的转轴、采样频率为12 kHz和48 kHz的驱动端轴承和采样频率为12 kHz的风扇端轴承。该轴承数据集包含正常数据4个、外圈故障数据77个、内圈故障数据40个和滚动体损伤数据40个。故障类型包括正常、滚动体故障、内圈故障和外圈故障。本文选取1组正常数据、3组不同故障深度的滚动体故障数据、3组不同故障深度的内圈故障数据和3组不同故障深度的外圈故障数据为研究对象，故障深度分别为0.177 8、0.355 6 mm和0.533 4 mm。

图5 轴承实验台

2.2 故障诊断实验

具体的实验步骤如下。

(1)如表1所示，本文分别选取12 kHz驱动端的10组数据，将这10组数据划分为4类标签，即正常(类0)、滚动体故障(类1)、内圈故障(类2)和外圈故障(类3)。然后将10组数据竖向堆叠成一维数据并均等拆分成多组小数据集，改变这些小数据集的顺序，并将这些数据集划分成三等份，前两份作为训练集，后一份作为测试集。向训练集和测试集数据中加入噪声干扰(信噪比为10 dB)，然后对含噪声数据进行一定程度的随机损坏，损坏程度设置为60%(即将60%的数据随机置零)。

表1 轴承故障数据

(2)使用CDAE-DBN融合模型处理训练集。以含有噪声的信号为输入数据，原始信号为标签，均方误差(mean squared error，MSE)为预测指标。采用CDAE提取浅层特征信息，其学习率为0.001；采用DBN提取深层特征信息，DBN中两个RBM的隐藏层节点数分别为500和300，DBN学习率为0.005，训练批次为270次。

(3)利用softmax分类器基于深层特征信息进行分类，并计算训练损失和精度。

(4)使用测试集数据验证CDAE-DBN融合模型的有效性，并计算训练损失和精度。

(5)对比CDAE-DBN融合模型和DBN模型的故障诊断精度，进一步验证本文所提方法的有效性及鲁棒性。

2.3 结果分析

2.3.1融合模型过程可视化

(1)t-SNE

t-SNE(t-distributed stochastic neighbor embedding)是一种常用的非线性降维技术,主要用来对高维数据进行可视化。为了能够直观反映CDAE-DBN融合模型的轴承故障诊断效果，使用t-SNE对其进行降维，将高维数据降为二维平面散点图，通过这些散点图能够直观地看到故障诊断过程中每一步数据的详细情况，并可以分析模型的特征提取能力。

图6为未经处理的原始数据t-SNE图，图7为原始数据经CDAE处理后得到的浅层特征t-SNE图，图8为浅层特征数据经DBN处理后得到的深层特征t-SNE图。从图6～8中可以看出，原始状态下不同故障类型的数据完全叠合在一起，无法识别；经过CDAE处理后叠合在一起的数据按照不同故障类型开始分散；再经过DBN处理后不同故障类型的数据聚集在一起，这说明融合模型具有较强的特征提取能力和较高的故障识别精度。

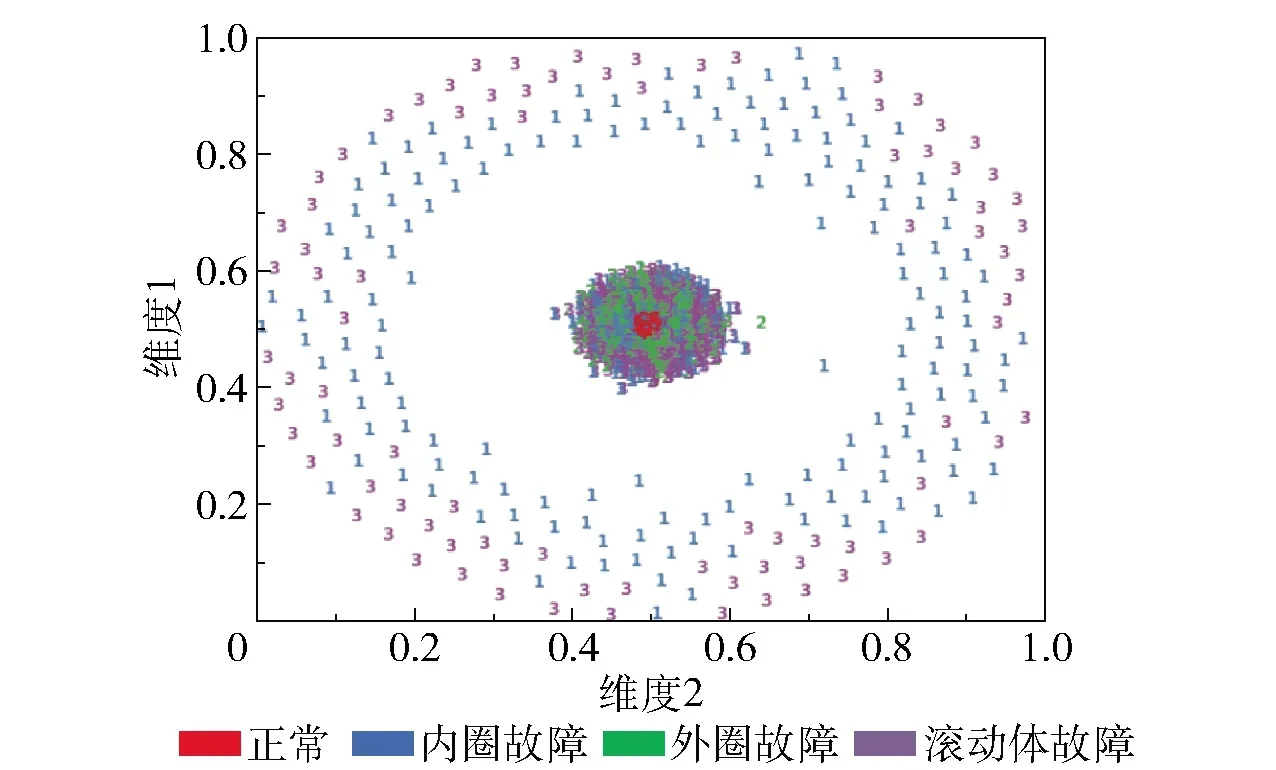
图6 原始数据t-SNE图

图7 CDAE提取的浅层特征t-SNE图

图8 CDAE-DBN分类t-SNE图

(2)ROC

受试者工作特征曲线(receiver operating characteristic curve，ROC曲线)是能够比较诊断测试效果的一种方法，其纵轴和横轴分别表示数据分类的真正例率和假正例率，可用来描述数据的正相关和负相关。ROC适用于二分类网络，对于多分类网络，ROC首先将多分类网络转变成多个二分类网络，然后分别绘制这些二分类网络的ROC曲线，最后计算曲线的平均值，即得到多分类网络的ROC曲线。ROC曲线越靠近正相关(曲线越偏上且区域值越接近1)说明网络特征提取效果越好且分类的精度越高。

图9为原始数据ROC曲线。从图中可以看出每个二分类ROC曲线和平均ROC曲线都趋于对角线，正相关和负相关均有，这表明原始数据的分布是杂乱无章的。图10是经CDAE处理后的浅层特征的ROC曲线，曲线虽均呈正相关，但每条ROC曲线分割的区域面积S都相对不太大，表明数据的分类精度不高，这说明CDAE可以提取振动信号的有效特征。图11是浅层特征经DBN处理后的ROC曲线，可以看出每条ROC曲线都非常趋近左上角，说明数据的分类精度较高。可见CDAE-DBN融合模型的特征提取能力更强，能够从受噪声干扰的振动信号中提取有效特征。

图9 原始数据ROC曲线

图10 CDAE处理后的浅层特征ROC曲线

图11 CDAE-DBN处理后结果的ROC曲线

2.3.2效果对比

(1)精度与损失函数

在分类问题中，精度更加直观，也更具有可解释性，而损失函数有助于对模型进行评估，并且可为模型参数的优化提供方向。图12和图13分别是轴承故障诊断结果的精度与损失函数对比。从图中可以看出，在精度方面，CDAE-DBN融合模型高于DBN模型，而在损失函数方面，CDAE-DBN融合模型低于DBN模型。

图12 精度对比

图13 损失函数对比

为了能够更加客观地验证融合模型的诊断能力，这里引入箱型图。箱型图由上下边缘线、上下四分位数和中位数组成(重复多次实验后得到多次实验的精度结果的数组，其中上下边缘线分别为最大和最小精度，上下四分位数分别为精度数组的上下四分位数，中位数为精度数组的中位数)，如图14所示，图中数据包括10组DBN模型精度结果和10组CDAE-DBN融合模型精度结果。箱子的位置越高表明该方法的精度越高，显然CDAE-DBN融合模型的精度优于DBN模型。

图14 精度箱型图

(2)混淆矩阵

混淆矩阵可用来衡量一个网络模型分类的准确程度。图15(a)为DBN模型诊断结果的混淆矩阵，图15(b)为CDAE-DBN融合模型诊断结果的混淆矩阵。其中标签0、1、2和3的定义见2.2节。从图15(a)、(b)的对比可以看出除了无故障的分类精度不变，其他故障种类的精度均有所提升，其中第1类滚动体故障和第3类外圈故障的精度提升较大，这两类分类结果的精度分别从0.80和0.87增加到0.96和0.94；第2类内圈故障的精度也有小幅度提升，其值从0.95增加至0.99。这表明与DBN模型相比，CDAE-DBN融合模型具有更高的故障识别精度，同时也验证了融合模型的有效性及实用性。

图15 DBN模型和CDAE-DBN融合模型的分类结果混淆矩阵

(3)信噪比与分类精度

当输入不同信噪比的数据时，CDAE-DBN融合模型和DBN模型的分类精度对比如图16所示。由图可见，在信噪比由-8 dB到10 dB的变化过程中，CDAE-DBN模型的故障识别精度均高于DBN模型。特别地，当输入数据的信噪比为10 dB时，CDAE-DBN模型的故障诊断精度达到0.97，而DBN模型的诊断精度只有0.89。

图16 不同噪声水平下CDAE-DBN融合模型与DBN模型的精度对比

3 结论

在滚动轴承故障诊断中，如何从受噪声干扰的振动信号中提取关键的特征信息一直是研究的热点。针对DBN模型的局限性，本文提出一种基于CDAE-DBN的深度融合模型，并应用于机械设备的故障诊断。CDAE能够降低信号中的噪声干扰并自适应地提取滚动轴承振动信号的浅层特征，在此基础上，DBN学习深层特征并输出故障识别结果。实验结果表明所提融合模型在噪声干扰下对故障类型具有更高的识别精度，优于传统的单一深度学习模型。