福州市商家对“禁塑令”的实施情况调查研究——基于结构方程模型的分析

张丹娥，连晴滔，屈 文

（闽南理工学院，福建 石狮 362700）

随着生态环境形势的日益严峻，国内外对环境保护的要求日趋增高，国家发展和改革委员会、生态环境部等九部门联合印发《关于扎实推进塑料污染治理工作的通知》。随后，各地区接连印发了一系列相关的治理实施办法。而作为“禁塑令”政策实行中不可缺少的一环，商家是否切实执行“禁塑令”对塑料污染治理工作有着显著影响。本文在充分掌握实地调查数据的基础上，从商家的角度出发，调查福州市“禁塑令”政策颁布后餐饮行业各商家的实施情况、塑料制品使用状况，并对政策实施过程中出现的问题进行调查研究，找出相应的解决方案，帮助“禁塑令”更好地落实，推进国家塑料污染治理。

1 商家对“禁塑令”实施情况的调查指标体系构建

“禁塑令”的实施情况受多方面的因素影响，各要素之间相互联系但又各自独立。本调查主要关注点为商家的实施问题，因此，根据影响要素构建了商家对“禁塑令”实施情况的调查指标体系。通过该体系进行分析，查阅了相关商家实施调查问卷，并结合实际情况，进行了调查问卷的设计，问卷主要分为基本信息、影响情况、商家行为、发展推想四个部分，涉及18 个问题。2021年7月进行了首次预调研，随后根据问卷填写情况对问卷部分问题重新进行权衡和调整。2021年8—9月进行正式调研。本次调查通过问卷星向福州市区及所辖各县市发布网络调查问卷，共回收问卷500 份，有效问卷为482 份，有效率为96.40%。

2 基于结构方程模型分析的商家实施情况研究

商家的实施情况直接关乎“禁塑令”的推行效果，商家的实施度越高，政策的推行效果越好。本文以福建省福州市为例，利用结构方程模型分析法研究商家实施情况。其间观察商家实施“禁塑令”的效果，找出影响商家实施的主要因素，然后提出有效对策，通过提高商家的实施度来提升“禁塑令”推行效果。

2.1 研究方法

2.1.1 变量设置

选取商家实施度作为因变量，即被解释变量。在借鉴相关研究成果的基础上，结合实际调研情况，选取基本信息、影响情况、商家行为和发展推想（共计4 个维度、8 个测量指标）作为影响商家实施度的因素，即自变量，对因变量进行解释，如表1所示。

表1 测量指标设置

2.1.2 模型的选择

结构方程模型是当今统计方法的一大发展，它把测量方程完美地结合起来，成为多变量数据分析的重要手段之一。其出发点是被测量指标的协方差矩阵是一组待估计参数的函数，如果模型是正确的，那么总体的协方差矩阵就能够被准确地推理出来，即有∑=∑()。其中，∑是被观察的总体的协方差矩阵，用样本协方差矩阵替代；是个矢量，含有模型的待估计参数；∑（）是作为的函数写出的方差-协方差矩阵，根据∑=∑()，两个矩阵相等，则其相应位置元素相等，可以求出待估计的参数。

2.2 研究过程

2.2.1 模型假设

根据餐饮行业商家的问卷及访谈分析，提出在“禁塑令”施行时期受环境影响的框架中4 个主范畴之间的研究假设，如表2所示。

表2 主范畴之间的研究假设

2.2.2 量表信效度分析

自变量的信度检验如表3所示。除基本信息外，各个自变量的克朗巴哈系数均大于0.7，表明这些自变量的可靠性较高，可纳入模型路径图中。在构建结构方程模型前，运用SPSS 软件对数据进行探索性因子分析，探究主要影响因素，找出模型中的潜在变量，减少题项的数目，使之变为一组较少而彼此相关性较大的变量。

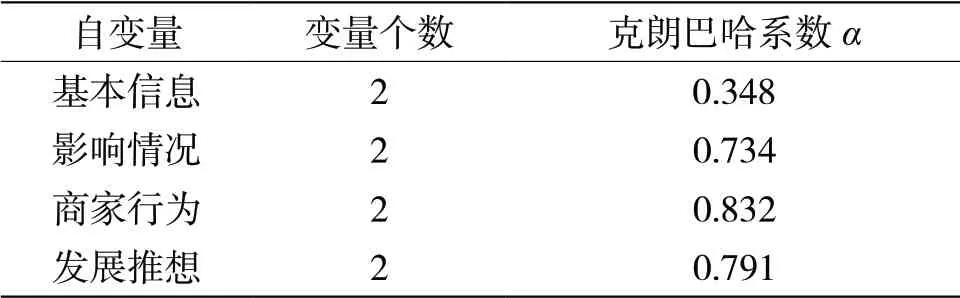
表3 自变量的信度检验

首先进行KMO 检验和Bartlett 球形检验分析，如表4所示。KMO 检验值为0.818，值小于0.001，可认为所选题项之间有共性，适合做因子分析。影响情况、商家行为、发展推想是根据旋转后的因子负荷矩阵定义的3 个因子，三者涵盖了影响商家“禁塑令”执行状况的直接和间接因素。本模型主要从商家“禁塑令”执行情况的评价入手，建立结构方程模型来探讨各因素的关系，并进行实证研究。

表4 KMO 检验和Bartlett 球形检验的结果

2.2.3 实证分析

使用AMOS25.0 软件进行数据分析，标准化拟合参数结果如表5所示。其中，为自由度，是最常报告的拟合优度指标，与自由度一起使用可以说明模型正确性的概率，/是直接检验样本协方差矩阵和估计方差矩阵之间的相似程度的统计量，其理论期望值为1；为近似误差的均方根；为拟合优度指数，为规范拟合指数，为Tucker-Lewis指数，为递增拟合指数。

表5 拟合指标

结果表明，基本信息对“禁塑令”执行状况有显著正向作用（回归系数=0.19，概率＜0.001），假设1 得不到验证。假设2 至假设4 均得到验证，影响情况、商家行为和发展推想都对“禁塑令”执行状况有显著正向作用（分别为0.45、0.52 和0.49，＜0.001）。基本信息对影响情况有显著正向作用（=0.21，＜0.001），假设5 得不到验证。商家行为对影响情况和发展推想均有显著正向作用（分别为0.42 和0.45，＜0.001），假设6 和假设7 得到验证。表5 显示，/值小于3，均方根残差（）小于0.05，值小于0.080，符合标准要求，模型的拟合参数、、和均大于0.900，整个模型的拟合度较好。

2.2.4 模型结构分析

一是影响情况对“禁塑令”执行状况的作用。影响情况包括塑料制品的消耗情况和“禁塑令”执行后对店铺的影响两个类属。根据结构方程模型的验证结果，影响情况对“禁塑令”执行状况有显著的正向作用。二是行为状况对“禁塑令”执行状况的作用。行为情况包括塑料制品更换情况和塑料垃圾处理情况两个类属。根据结构方程模型的验证结果，行为状况对“禁塑令”执行状况有显著的正向作用，且数值较高。

3 对策建议

3.1 积极配合政府开展宣传工作

在政府“禁塑令”的宣传过程中，商家作为实施主体之一，应积极配合政府工作，将政策落到实处，可自行设计环保且人性化的产品包装，将相关环保知识体现在包装上，使消费者更容易接受环保知识。例如，在商品包装上添加趣味性的环保问题，形成商店自身的固定风格，增强消费者主动学习环保知识的兴趣。

3.2 寻找更加合适的塑料替代品

在商家经营过程中，可以设立意见箱，及时收集消费者的反馈意见，根据消费者的建议选择更加合适的替代品。同时，商家应积极推广可循环、易回收、可降解的替代产品，引导人们少用不可降解塑料产品。例如，餐饮类商家应主动供应环保型包装，鼓励消费者自带餐具并提供优惠。

3.3 增强社会责任感

商家应该提升自己的整体意识，增强社会责任感，自觉学习环保知识，树立环保意识。例如，商家可设置激励机制，将“禁塑”行动列入员工的绩效考核，并设立“奖金池”等激励方式，激发员工的“禁塑”宣传动力，培育内部“禁塑”文化。