基于静载试验的I型钢-混组合梁桥的荷载横向分布研究

张国平，张钦宇，朱洲洲

(湖北交通工程检测中心有限公司，湖北 武汉 430200)

0 引 言

装配式钢-混组合梁桥，由于其自重轻、可在工厂流水化制造，施工工艺简单等优点，可以实现桥梁工业化建造以及快速施工。对于装配式多主梁钢-混组合梁桥，主梁之间通过横向联系、主梁与桥面预制板通过剪力钉形成整体，共同承受外部荷载，因此，横向联系的好坏直接影响了桥梁整体的承载能力。我们通常希望多主梁受力变形协调一致，各主梁受力均匀。对于装配式多主梁混凝土桥梁，在设计时一般将不同的主梁赋予不同的横向分布系数,将空间结构问题转换为简单的平面杆系结构计算，且设计通常比实际受力偏安全[1]。

目前，国内外针对多主梁结构横向分布的计算理论较多，并且有很多学者通过工程实例验证了相关计算理论的适用范围。国内通常计算桥梁横向分布系数的方法包括杠杆原理法、偏心压力法(或修正的偏心压力法)、铰接板(梁)法、刚接梁法、比拟正交异性板法(G-M法)等。陈勇军等[2]采用传统横向分布系数计算方法与有限元分析法进行对比分析，得出采用“G-M”法计算20 m标准跨径桥梁的横向分布系数误差最小。闫林君等[3]针对不同跨径、不同主梁间距、不同主梁数的钢-混组合梁应用经典横向分布系数计算方法进行分析，并与有限元建模分析对比，指出传统横向分布计算理论不足之处，提出了适用于钢-混组合梁横向分布系数的通用计算公式。唐治军等[4]通过荷载试验验证ANSYS有限元法、刚接梁法在现浇桥面板Ⅰ型组合混凝土桥梁上应用的可靠性。韦立林[5]等对简支空心板桥进行荷载试验测试桥梁的横向分布系数。但目前尚未有工程人员通过I型钢-混组合梁工程实例验证传统横向分布计算理论的适用范围。本文利用有限元分析软件Midas Civil建立30 m跨径的装配式I型钢-混组合梁桥结构模型，并计算出横向分布系数，同时通过对实桥进行现场静载试验，实测钢-混组合梁在各工况下的挠度值反算桥梁荷载横向分布系数，并与传统计算方法、有限元法进行对比，从而验证上述横向分布计算理论和有限元法的有效性。

1 不同计算理论对比

1.1 工程实例概况

本研究选用的工程案例为位于湖北省江北东高速公路的某桥梁，其上部构造采用[6×30+4×(5×30)+3×40+6×(5×30)+3×40+5×30+4×30+3×40+5×30+4×40]m十八联简支桥面连续钢-混组合梁，交角90°，桥面净宽为2×净11.75m。主梁横向布置为4片Ⅰ型钢-混组合梁，其中30 m跨径的桥梁Ⅰ型钢主梁梁高为1.4 m，40 m跨径的桥梁Ⅰ型钢主梁梁高为1.8 m，桥梁横断面如图1所示。桥面板均采用C55混凝土，钢主梁为Q345qD钢材。桥梁设计荷载等级为公路—Ⅰ级。

图1 Ⅰ型钢-混组合桥梁横断面示意图

主梁采用“开口钢板梁+混凝土桥面板”的钢-混组合梁，横向每2片工字型钢主梁组成一榀吊装结构，两榀间横向采用湿接头连接。每两榀间钢横撑10 m左右设一道。榀内横撑每5 m左右设一道。钢筋混凝土桥面板厚23 cm，榀间组合梁吊装就位后，通过现浇微膨胀混凝土湿接头形成整体，钢梁和钢筋混凝土桥面板通过布置在钢梁顶板处的焊钉剪力键形成组合梁。

1.2 桥梁荷载横向分布系数计算

采用不同横向分布系数计算方法，计算本项目Ⅰ型钢-混组合梁桥的荷载横向分布系数。

1.2.1 有限元法

采用MIDAS Civil建立了30 m钢-混组合梁空间梁格有限元模型。利用Civil截面特性计算器，按照刚度等效原则，将混凝土面板截面换算为钢截面，形成换算截面；主梁、钢横撑均采用梁单元模拟，混凝土桥面板采用虚拟横梁连接，钢主梁、钢横撑与桥面板虚拟横梁的连接直接采用刚性连接模拟，桥梁支座采用一般支撑模拟。同时模型中，忽略桥面板和钢主梁之间的相对滑移效应。该计算方法在文献[6]被证明其有效。跨径为30 m的钢-混组合梁有限元模型如图2所示。根据桥梁荷载横向分析系数的定义，依次对各片主梁施加集中力10 kN，查看各主梁的控制截面的位移或应变值，如图3所示；并参考公式(1)计算荷载横向分布系数竖标值[7]。

图2 Midas Civil钢-混组合桥梁有限元模型图

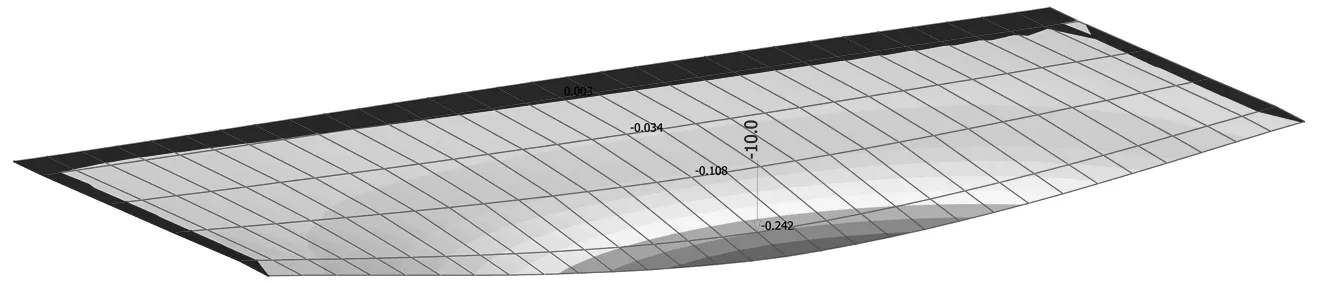
图3 集中力施加在1号梁时跨中截面位移等值线

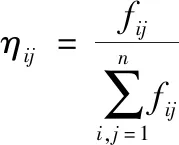
(1)

式中：ηij为在主梁1/4截面或跨中截面横向影响线竖标值；fij为集中力作用在i号梁上时j号梁产生的位移或应变值；n为主梁片数。

集中力作用下各主梁横向分布影响线竖标值，见表1。

表1 30 m钢-混组合梁集中力作用下1/4截面、跨中截面横向分布影响线竖标

根据各主梁横向分布影响线竖标，绘制各主梁的横向分布影响线。对横向分布影响线，按照最不利布载原则，参考公式(2)计算各主梁横向分布系数mi。其中1#、2#梁横向分布计算最不利布载如图4所示。

图4 主梁横向分布系数计算图示

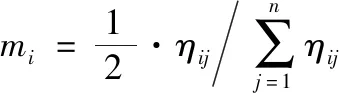
(2)

式中：ηij为i号梁横向影响线上各车轮对应横向影响线竖标值；n为车轮总数量。

各主梁荷载横向分布系数计算结果见表2。

表2 有限元法横向分布系数计算结果

1.2.2 传统横向分析系数计算法

传统横向分布系数计算方法，按照文献[1]，支点截面采用杠杆原理法；1/4截面至跨中截面，可根据适用条件选择偏心压力法、修正的偏心压力法、铰接板梁法、刚接梁法、“G-M”法。由于本项目桥梁主梁横向连接较多，显然铰接板梁法不合适，本文仅探讨偏心压力法、修正的偏心压力法、刚接梁法、“G-M”法对30 m钢-混组合梁横向分布系数计算的适用性。30 m钢-混组合梁桥传统横向分布系数计算见表3。

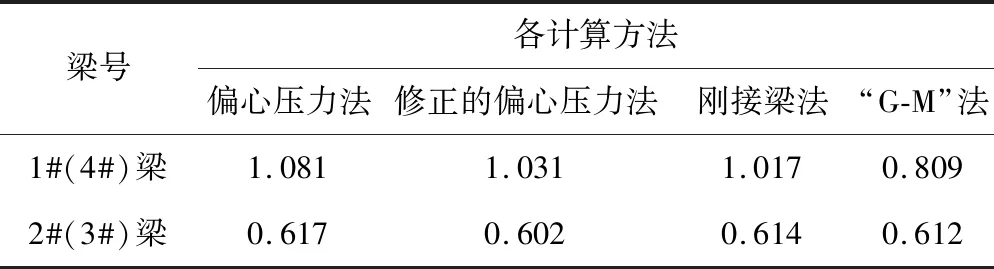
表3 传统方法计算横向分布系数

2 荷载横向分布静载试验

桥梁荷载试验分为静载试验和动载试验两部分。静载试验是通过桥梁加载试验，实测桥梁在各工况荷载作用下的结构挠度、应变，并与模型理论计算值进行比较，检验桥梁结构实际承载能力是否满足设计要求，同时还可以得到桥梁整体结构的位移、应变纵横向曲线反应。而动载试验是检验桥梁结构在环境激励或行车荷载下动力响应。故本文主要通过静载试验研究Ⅰ型钢-混组合梁荷载横向分布特性。

2.1 静载试验工况及加载车辆

本次静载试验采用分级加载方式，测试试验桥跨在车辆荷载作用下各测点的应变、挠度及残余值。根据《公路桥梁荷载试验规程》(JTG/T J21-01—2015)有关规定，静载试验效率取0.85～1.05[8]。

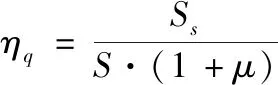
(3)

式中：Ss为静载试验荷载作用下，某一加载试验项目对应的加载控制截面内力或位移的最大计算效率值；S为控制荷载产生的同一加载控制截面内力或位移的最不利效应计算值；μ为按规范取值的冲击系数值。

本次静载试验采用400 kN双后轴加载车，加载车轴重及轴距分布见表4。

表4 加载车轴重、轮距分布

在保证静载试验效率前提下，按照荷载等效原则以及主梁最不利受力原则，确定本次桥梁静载试验分为4个工况，分别为跨中截面1#梁最大正弯矩工况、2#梁最大正弯矩工况、1/4截面1#梁最大正弯矩工况以及2#梁最大正弯矩工况。静载试验理论控制内力值和试验荷载等效值，以midas Civil建立的有限元法模型计算。静载试验工况内力值及加载效率见表5。桥梁各工况加载车载位布置图，如图5、图6所示。

表5 静载试验工况及试验效率

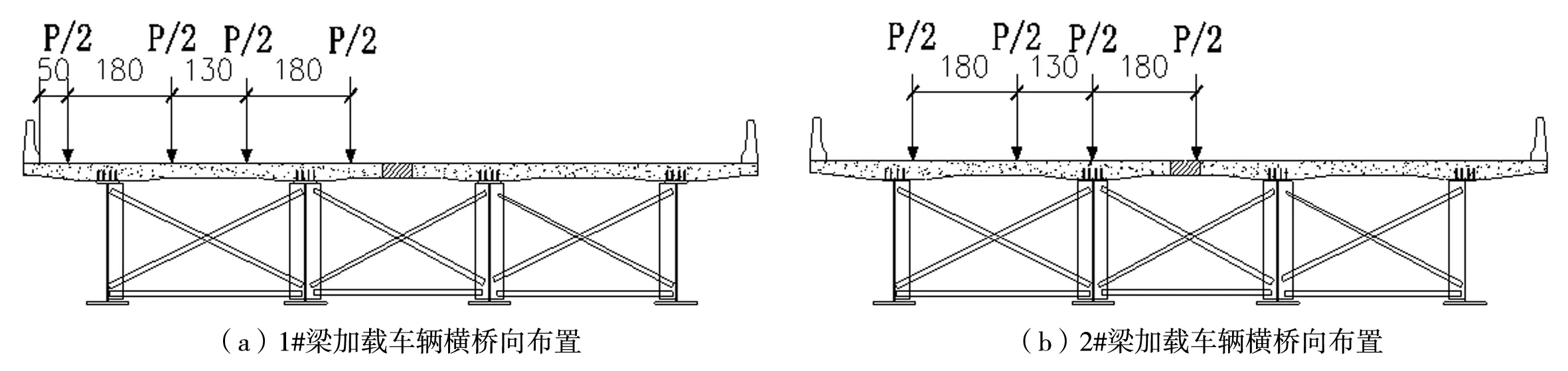
图5 30 m钢-混组合梁荷载横向布载图(单位：cm)

图6 30 m钢-混组合梁静载试验纵向布载图(单位：cm)

2.2 试验测试内容及测点布置

本次静载试验，主要测试钢-混组合梁加载后的跨中截面、1/4截面挠度和应变，观测卸载后的桥梁状态恢复状况。各测试断面每片梁底设置挠度测点1个，共计8个挠度测点；各测试断面每片梁底设置应变测点1个，共计8个应变测点。其中挠度测试采用位移传感器测试、应变测试采用东华DH3819无线静态应变仪进行测试。为消除温度对静载试验结果的影响，本次静载试验选择在气温较低且平稳的晚上进行。

2.3 静载试验结果分析

表6列出了各静载试验工况下，实测各主梁的挠度最大值以及校验系数。根据《公路桥梁荷载试验规程》，对于钢桥结构静载试验挠度校验系数为0.75～1.0，混凝土结构静载试验挠度校验系数为0.50～0.90，本次静载试验挠度校验系数介于两者之间，均满足规范要求，同时桥梁结构的相对残余值均小于20%，说明卸载后桥梁的性能状态恢复良好。

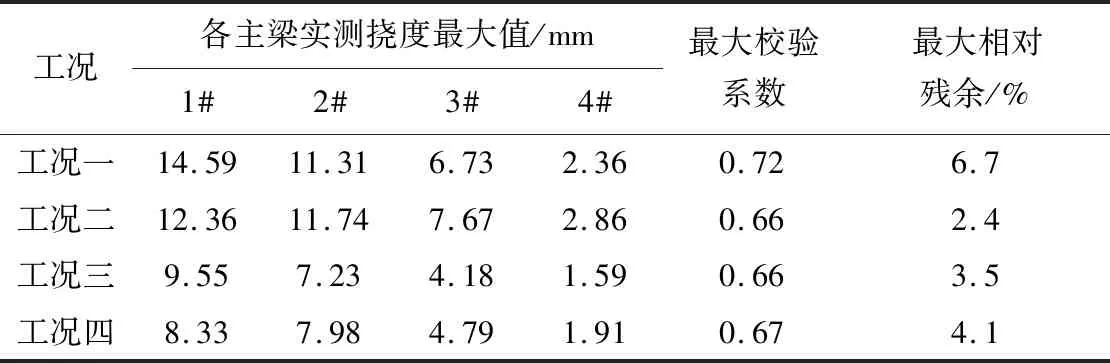
表6 静载试验主梁挠度统计表

3 综合对比分析

为评价静载试验结果和理论计算结果的吻合程度，根据静载试验结果反算各主梁荷载横向分布系数，并与前文4种传统横向分布计算方法及有限元模型的计算结果进行对比，得到跨中截面和1/4截面荷载横向分布系数综合对比表，见表7、表8。图7、图8为有限元法、G-M法、偏心压力法、修正的偏心压力法、刚接梁法计算的荷载横向分布系数与静载试验实测的荷载横向分布系数对比图。

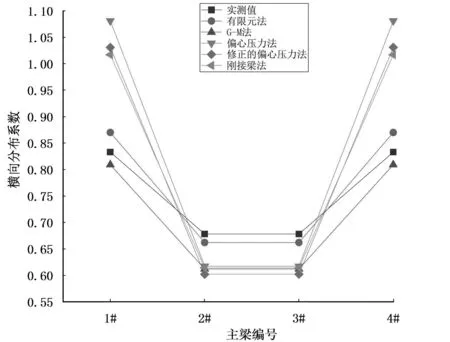
图7 跨中截面1#～4#梁荷载横向分布系数对比

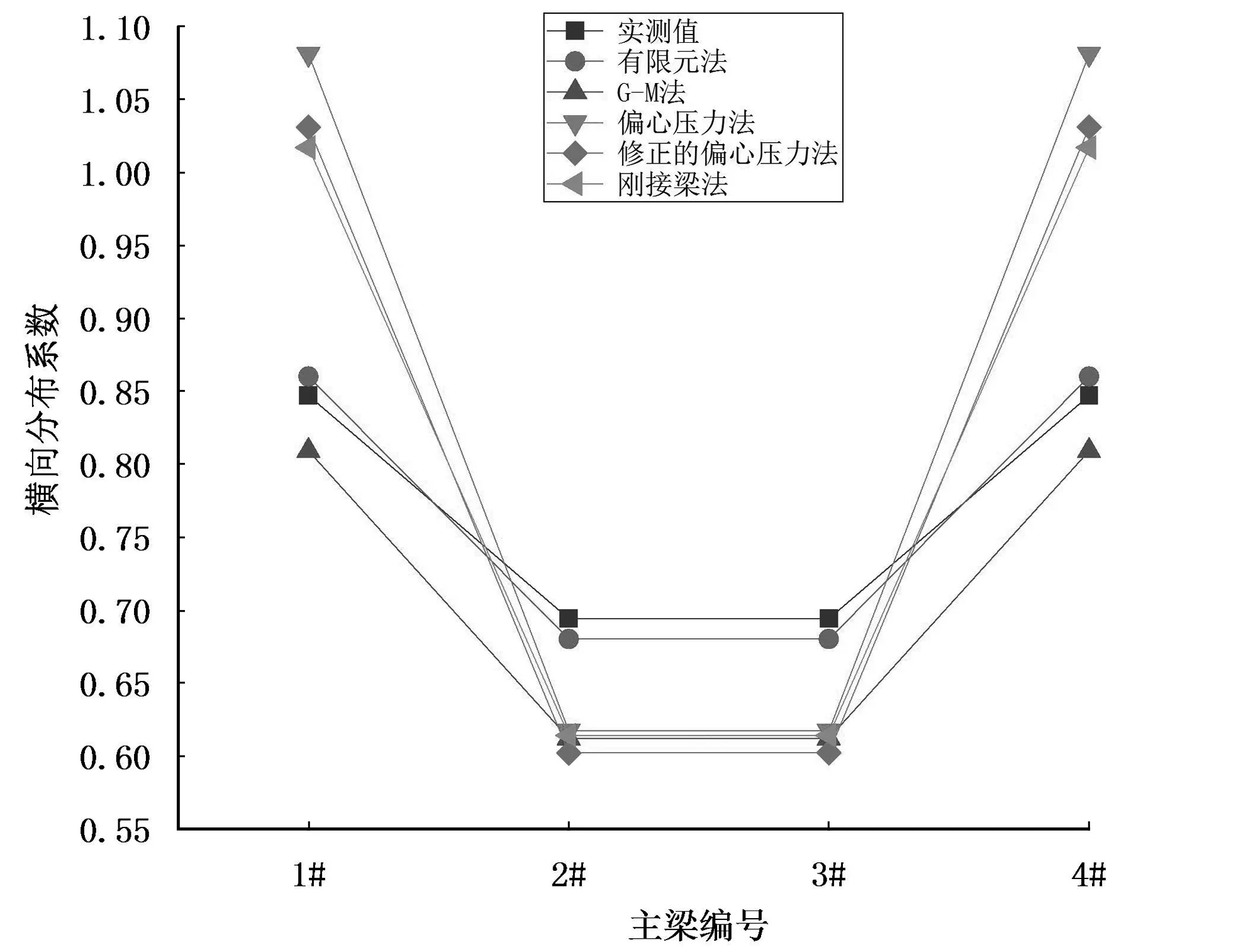
图8 1/4截面1#～4#梁荷载横向分布系数对比

表7 跨中截面横向分布系数综合对比

表8 1/4截面横向分布系数综合对比

从表7可以看出，对于跨中截面，偏心压力法、修正的偏心压力法、刚接梁法横向分布计算结果与实测结果偏差较大，最大偏差达到了29.77%。G-M法和有限元法计算结果与实测值偏差相对较小，其中G-M法最大偏差为-9.73%。

从表8可以看出，对于1/4截面，同样偏心压力法、修正的偏心压力法、刚接梁法横向分布计算结果与实测结果偏差较大，最大偏差达到了27.63%。G-M法和有限元法计算结果与实测值偏差相对较小，其中G-M法最大偏差为-11.82%。

4 结 论

通过以上分析，可以看出：

(1)从静载试验挠度实测结果与理论计算对比分析，各测点校验系数和相对残余比均在规范允许范围内，证明桥梁承载能力满足设计要求，工作性能良好。

(2)从1/4截面和跨中截面的实测结果表明，荷载横向分布系数沿纵向是变化的，且1/4截面荷载横向分布系数比跨中截面稍大些；边梁的实测荷载横向分布系数比理论计算值要小，而中梁的实测荷载横向分布系数比理论计算值要大，说明实际横向联系要比理论计算要好。

(3)上述4种传统荷载横向分布计算方法，30 m跨径的Ⅰ型钢-混组合梁采用“G-M”法及有限元法计算的荷载横向分布规律，与静载试验实测变化规律一致性较好，偏差在15%以内；而对于偏心压力法、修正的偏心压力法以及刚接梁法计算结果与静载实测值偏差较大，最大偏差接近29.77%，设计时，采用此3种方法过于保守，对材料造成浪费。

(4)试验结果表明，对于30 m跨径的4片Ⅰ型钢-混组合梁桥型，跨中和1/4位置存在钢横撑，且宽跨比小于0.5时，当采用传统计算方法时，“G-M法”误差最小。